$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



第8章

生命中湧現的計算與演算法





In the first place, there can be no living science unless there is a widespread instinctive conviction in the existence of an Order of Things, and, in particular, of an Order of Nature.

回到起點來看，如果沒有一個普遍且直覺性的信念相信萬物及自然背後皆有序，那將不會有科學的存在。

Alfred Whitehead


生命科學和物質科學是現代科學的兩大樑柱，在歷史發展的洪流之下，各自的分支越走越細，漸漸讓兩邊越來越難互相溝通。許多新興的子領域(例如生物物理)漸漸開始扮演重要的橋樑，但是在大方向兩者仍具有非常不同的風格。相較於物質科學極力追求從底層由下而上且乾淨的形式化理解，生命科學在湧現(emergence)的浪潮下無法避免地需要面對複雜且多變的現象。同時，計算在兩者的研究中也逐漸扮演越來越重要的角色，也許計算的思考方式在未來能成為新的共同語言？

歡迎來到生命的世界

當我們從原子的尺度往上升，從宇宙的尺度往下降，在中間相會時，就抵達了生命世界的尺度。在這個既無法追蹤所有枝微末節又無法完全抽象掉細節的中間層次，生命以極為混亂卻又井然有序的方式環繞在我們身邊。

在本章中，我們將一改之前在數學及物理世界中建構理論大廈的作風，而是遊走於生命世界中不同的尺度，欣賞計算是如何悄悄地出現在其中。在旅程開始之前，讓我們先從稍微哲學的宏觀視角，剖析生命科學的經絡。

什麼是生命？

在演化生物學泰斗Ernst Mayer的著作『這就是生物學(This is biology)』中，他替“生命”一詞給出了以下的定義：

All these characteristics of living organisms distinguish them categorically from inanimate systems. A capacity
for evolution,
for self-replication,
for growth and differentiation via a genetic program,
for metabolism (the binding and releasing of energy),
for self-regulation, to keep the complex system in steady state,
for response to stimuli from the environment through perception and sense organs,
for change at two levels, that of the phenotype and that of the genotype.

以下所有生命有機體的特徵，明確地將他們和無生命系統區分開來。能夠
演化、
自我複製、
透過遺傳編程成長並且分化、
新陳代謝(能量的結合與釋放)、
自我控制，使得複雜的系統維持在平穩的狀態、
透過感知器官回應環境的刺激、
在表型和基因型這兩個層次上做改變。

Ernst Mayer

先暫且不論生命科學家之間也許會對這個定義有些歧異，光是從Mayer的嘗試中，我們就已經可以感受到生命世界和物理以及數學世界的極大區別。在先前數學及物理的章節中，我們看到如何透過公理以及數學模型，推導並建構出完整的世界觀。然而，在生命的世界中，人們距離這樣由下而上的理解還非常遙遠。這也預告了生命科學的學習方式將會與物理與數學不太一樣。

在接下來的篇幅中，我們將會看到大量的例子，由上而下慢慢地讓理解自然湧現。

生命科學的範圍

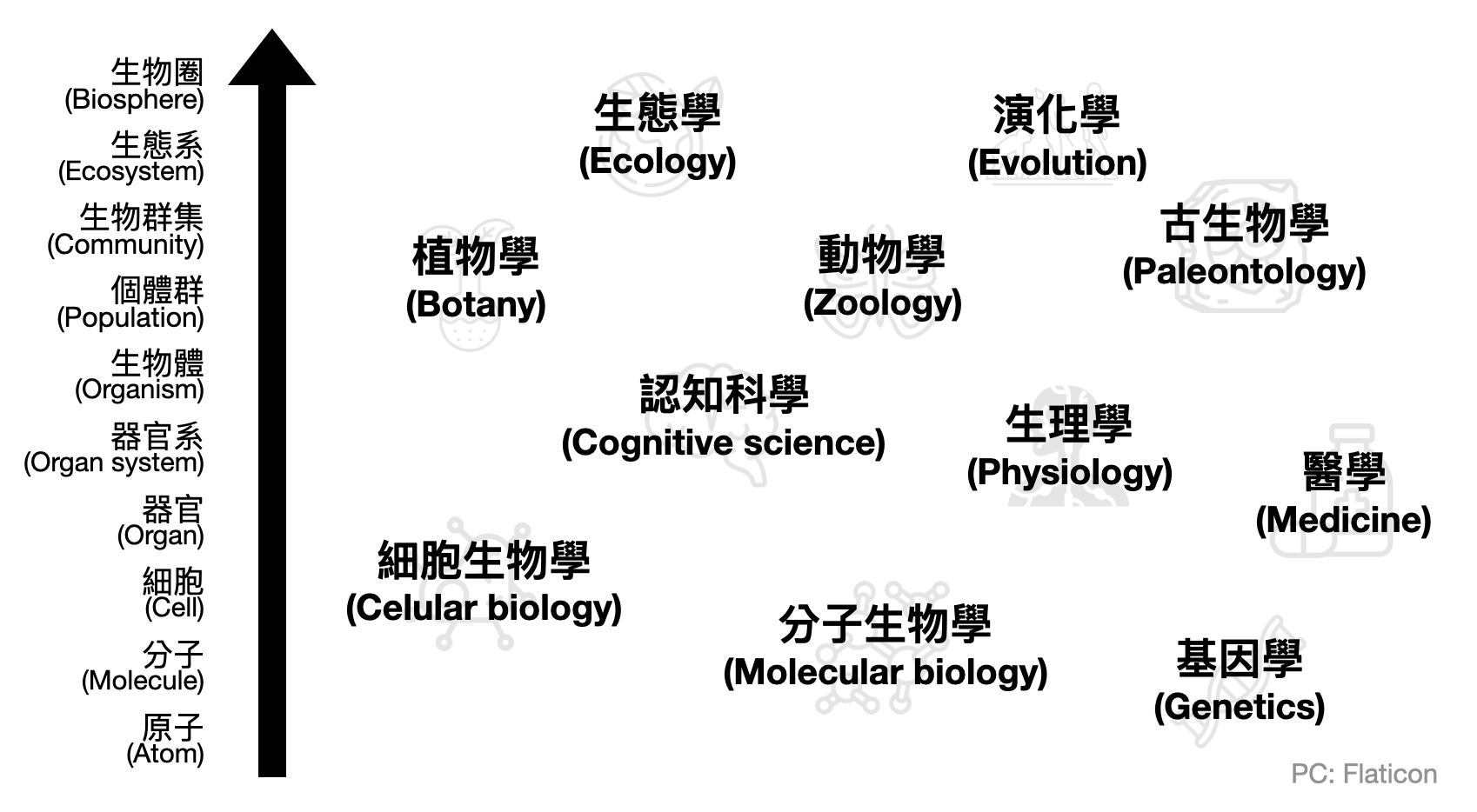
生命科學的範圍非常廣，和物理學一樣有著微觀到巨觀不同的尺度。同時，在中間的層次依據研究對象及研究方法論的不同，也分化出許多領域。

圖中嘗試依照各個領域所注重的階層做縱向劃分。

面對這樣如此複雜的學門，很容易一下就眼花撩亂，在之中迷失方向。分子生物學感興趣的課題和生態學十分不同，但兩者卻又可能互相提供新的思路與工具。所以對於像我一樣非生物專業訓練出生的讀者來說，我建議可以從以下兩個角度切入：

領域的核心範圍： 在現代科學的發展中，領域之間的邊界越來越模糊。然而對於每個領域和子領域來說，都還是有一個或多個“核心”。以分子生物學為例，在縱向尺度上它處於生物化學及遺傳學之間，於是外行人乍看之下，可能會覺得是不是只要把生物化學和遺傳學都學起來就懂分子生物學了。然而，當生物化學著重在化學過程，遺傳學研究生物體的遺傳與變異，分子生物學的核心則是生命活動(包含化學反應與遺傳機制)在分子層次上的機制。因此就算分子生物學的主要工具來自生物化學和遺傳學，其核心關注點是這兩個領域無法取代的。

領域的工具與方法論： 隨著科技的發展，帶來許多新的科學實驗和分析工具，並更進一步演化出新的研究方法論。於是對於同一個科學問題，開始會有各種不同的回答方式。例如想要解釋某個微生物的遺傳機制，既可以從傳統遺傳學或是分子生物學的角度下手，也可能可以利用演化的觀點切入，甚至在不久的將來或許可以直接用人工智慧模型模擬。這些不同的工具與方法論，並無高低之分。也正是因為有了這麼多不同的研究方法，擴展了我們對生命世界的理解。然而要小心的地方是，如何妥善的遊走於不同的技術和方法論之間，如果只是一昧的將所有工具都套入一遍，那得到的結果很可能像個大雜燴，反而失去了核心思想。

計算生物學

一說到計算與生物學，許多人的第一反應就是「計算生物學(computational biology)」這個學科。的確，在電腦科技蓬勃發展的時代背景之下，許多以“計算”作為開頭的子領域大量湧現，例如計算腦神經科學(computational neuroscience)、計算遺傳學(computational genomics)、計算解剖學(computational anatomy)等等。

在這些學科中，“計算”一詞通常指的是利用計算工具、資料分析、數學建模、數值模擬等等，來研究相對應的生物問題。

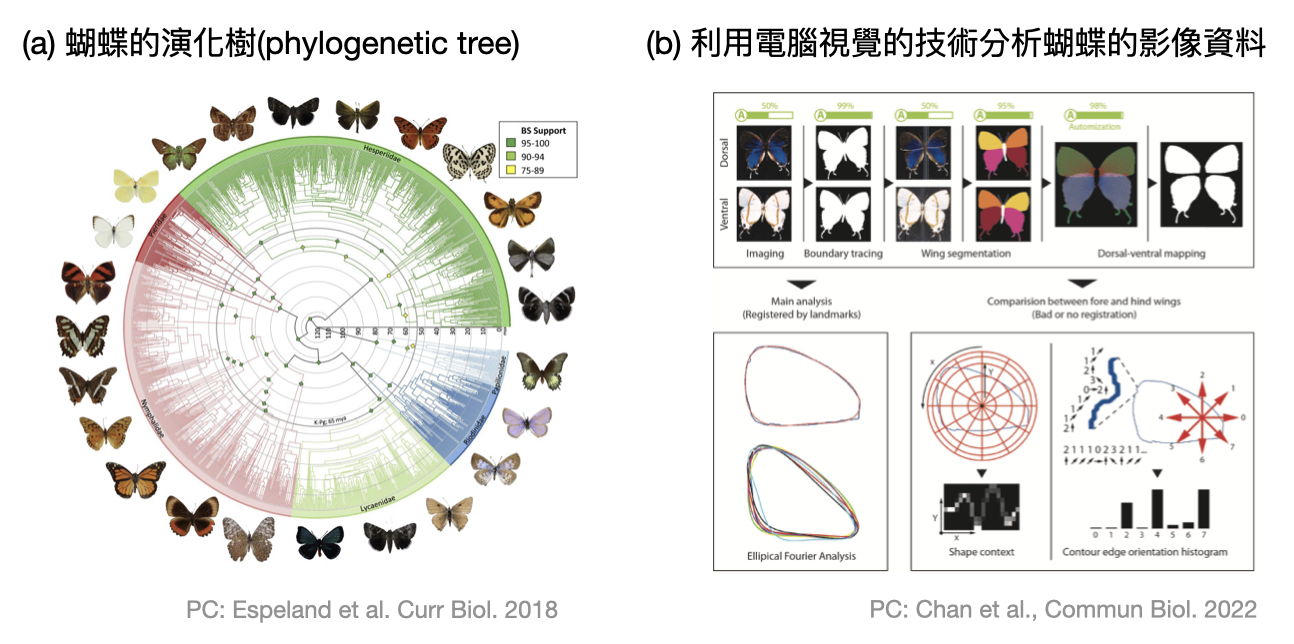
例如在演化生物學中，可以使用計算工具將不同物種根據基因序列之間的距離，畫出演化樹(phylogenetic tree, 例如下圖(a))。分析各種生物的影像資料時，可以透過電腦視覺的技術輔助(例如下圖(b))，以及使用資料分析方法抽取出關鍵的特徵值(例如下圖(c))。

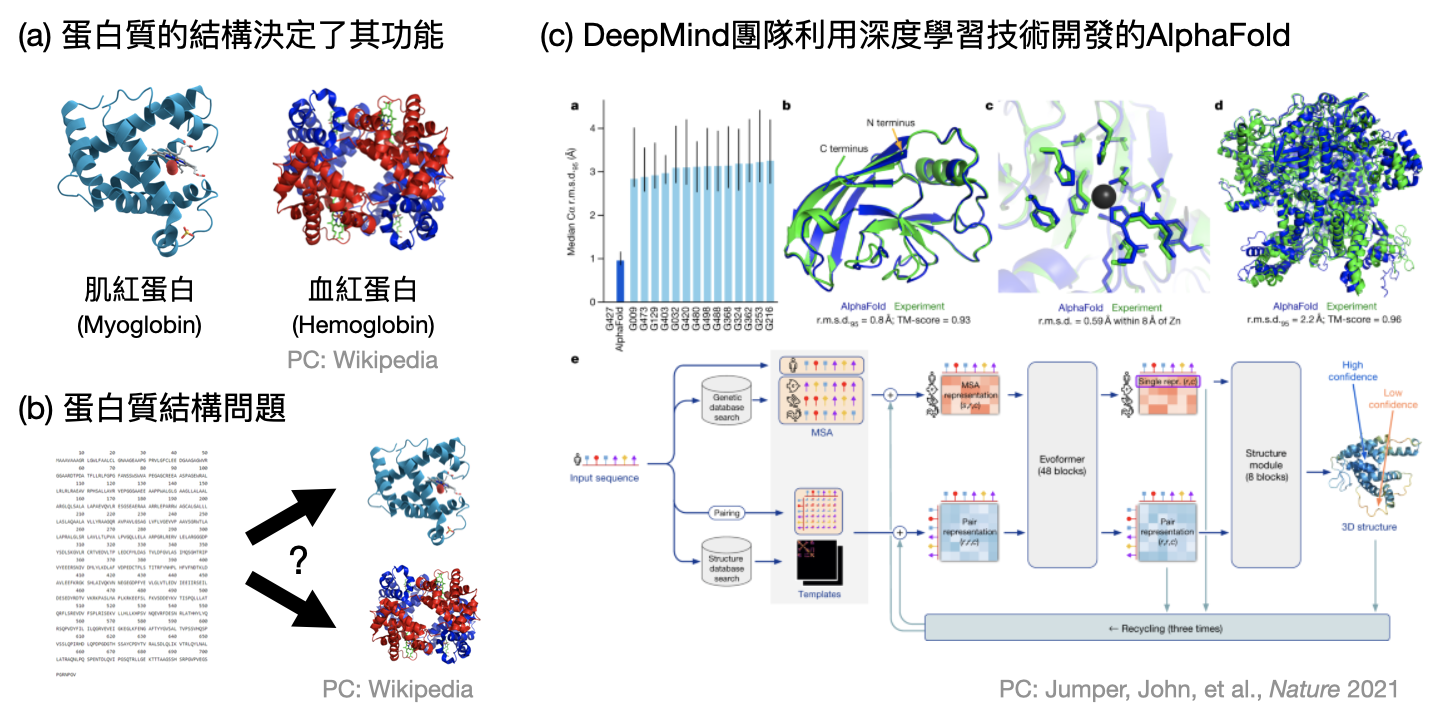
(a)電腦軟體可以幫助科學家處理繁雜的資料，並且在之上做計算，例如算出生物之間的演化樹(phylogenetic tree)。(b)機器學習可以進一步協助處理資料，例如使用電腦視覺的技術畫出蝴蝶各部位的形狀。

又或是近幾年來改變分子生物學研究規則的「AlphaFold」，是一套由人工智慧科技公司DeepMind開發出的程式，利用深度學習的技術，訓練出能夠根據氨基酸序列(amino acid sequence)推測出最終蛋白質3D結構的計算模型。其預測能力遠高於傳統的技術，徹底改變了分子生物學的樣貌。

上述兩個例子只是計算生物學中的鳳毛麟角，將計算方法應用在生物學的研究與新興學科，已經徹底改變了我們對生命世界理解的方式。不過，在本書剩餘的章節中，我們的重心將不在使用計算作為“工具”，而是使用計算這樣一個思考角度，來探索生命世界並試著提供新的理解。

(a)蛋白質的3D結構將決定了其功能。例如肌紅蛋白和血紅蛋白組成的分子很類似，但是因為結構的稍為不同，讓前者含氧能力比後者高出不少。(b)蛋白質的結構是由其氨基酸序列決定的。然而，如何從氨基酸序列計算出蛋白質的結構是個極為困難的問題。(c)DeepMind團隊利用深度學習訓練出具有極高成功預測率的模型。

什麼是“用計算的角度來提供對生命世界新的理解”呢？此時如果讀者感到困惑是十分正常的，先讓我們在抽象的討論上走最後一小段路，澄清這邊所指的“理解”到底是什麼意思。接著，我們將用大量的例子，來見識生命世界中的計算。

暖身：生物演算法和電腦演算法的比較

什麼是生命世界中的計算呢？在丟給讀者大量實例之前，先讓我們用個簡單的例子來暖暖身，並同時感受一下生物演算法和電腦演算法在做類似的計算時，做法可以有多麼不同！

之前我們看到了人工計算世界中最底層的語言是數位的二進位語言。有趣的是，生物世界中最底層的語言十分類似，一段遺傳編碼對應到了一串鹼基對(Base pair)，每個鹼基對由兩個核鹼基(Nucleobase)組成。核鹼基主要有五種：腺嘌呤(A)、胸腺嘧啶(T)、鳥嘌呤(G)、胞嘧啶(C)、尿嘧啶(U)。在“儲存一段訊息”時，相對應的DNA序列(這邊先暫時不討論RNA)會是兩串相互連接的鹼基對，而且相互連接的鹼基對會有特定的結構，例如：A和T必定相互連接成對、G和C必定相互連接成對。於是一個合法DNA序列可能如下： \begin{align*} &\text{ATCGATTGAGCTCTAGCG}\\
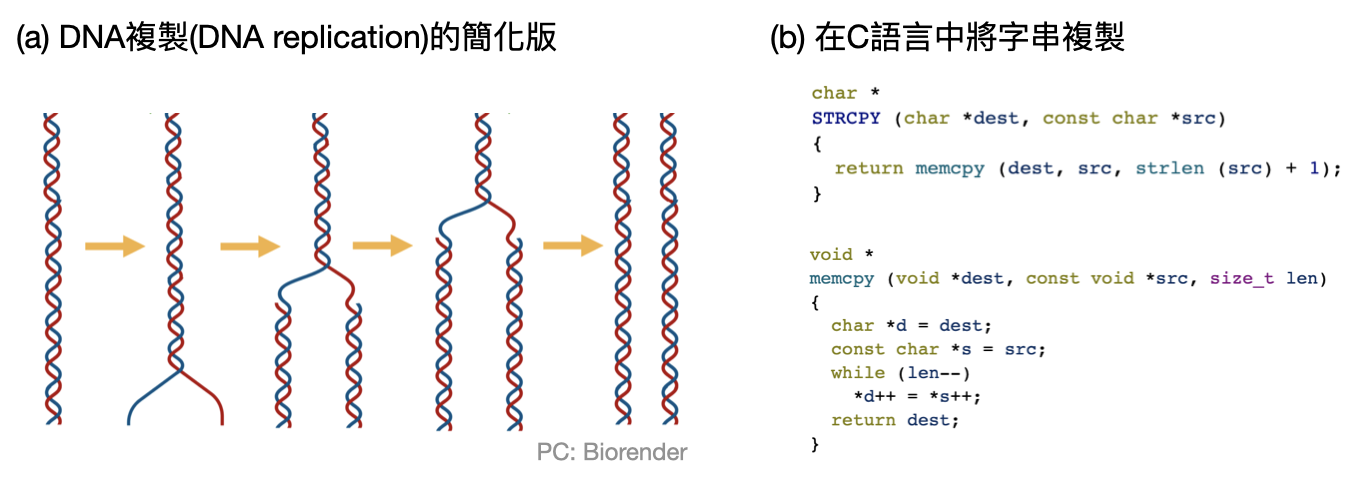
&\text{TAGCTAACTCGAGATCGC} \end{align*} 在生物中，這兩串相互連結的鹼基對串會形成所謂的雙股螺旋(double helix)結構，如下圖(a)所示。

(a)DNA複製的簡化版。雙股螺旋的“設計”使得複製的過程只要根據A和T、G和C的配對關係就可以達成。(b)在程式語言中的字串複製基本上是直接開一個新的記憶體，然後把想要複製的字串抄寫過去。

對於生物不熟悉的讀者這時候可能會問，為什麼要這麼麻煩用兩串鹼基對串來表示一段訊息呢？真正的原因可能沒有人會知道，不過這樣的結構馬上有個很好的功能：字串複製。

無論是生物個體的發展或是生殖中，複製遺傳物質中的訊息(也就是DNA序列)扮演著核心的角色，這又被稱為「DNA複製(DNA replication)」。在實際的生物體中，DNA複製具有繁雜的步驟，不過下圖(a)提供了一個簡化的版本。大致上來說，關鍵的步驟有兩個：(1)先將DNA序列的雙股螺旋結構像拉拉鍊一樣打開，(2)接著利用特殊的蛋白質將被拉開的鹼基對串根據A配T和G配C的規則形成新的雙股螺旋DNA序列。

字串複製同樣在電腦中扮演重要角色，你能想像你的生活中沒辦法使用“複製貼上”的功能嗎！？相較於生物世界中利用DNA的雙股螺旋結構，在電腦世界中訊息只會被一個字串存取。需要複製時，只要單純的將整個字串讀取一遍，然後寫在另外一個空白的字串上面就好了(如上圖(b))。

透過這個小例子，希望可以讓讀者感受到如何用計算的角度，抽象化思考一些生物世界中現象。從DNA和電腦程式是如何設計字串複製的演算法，我們也認識到根據不同的情景限制，甚至是一些隱藏的目的，生物世界中的計算和人工世界中的計算可以非常的不同(在量子物理的世界，甚至沒辦法有量子字串複製演算法呢)！

Marr的三階層分析

David Marr是個英年早逝的腦神經科學家。生於1945年，他在二十一歲時取得了劍橋大學的數學學士和碩士學位，並接著在博士研究上轉向理論腦神經科學。他的研究對大腦整體功能的理論和視覺神經系統都有極為開創性的貢獻，即使過了半個世紀仍然具有影響力。然而在1978年的冬天他被診斷了急性白血病，並在1980年去世。

Marr最著名的著作『視覺計算理論(Vision: A Computational Investigation into the Human Representation and Processing of Visual Information)』在他過世兩年後正式發表。在第一章中Marr討論了他的研究哲學與方法論，並提出了複雜訊息處理系統(complex information-processing systems)的三階層分析方法。雖然當時Marr主要想的研究對象可能是像大腦這樣極度複雜的訊息處理系統，然而生物研究中許多的課題在本質上也都具有複雜的湧現現象，因此很自然地也可以放入這個框架思考。

計算理論(Computational theory)： 系統中進行了什麼樣子的計算？計算的目的又是什麼？為什麼這樣的目的是合適的？是什麼樣子的邏輯和策略可以將這樣的計算實現？

表示與演算法(Representation and algorithm)： 計算理論可以如何被實現？其輸入和輸出是用什麼樣的表示方法(representation)？計算將輸入轉為輸出是用了什麼演算法？

硬體實作(Hardware implementation)： 表示和演算法是如何在實際情景中被實現的？

用Marr提出的這三個階層來分析本書第一部份提到的計算理論，可以發現由於一切的計算和分析都講究徹底的數學刻畫，於是我們可以同時對三個階層都有很完整的理解。然而一旦到了近年蓬勃發展的人工智慧，深度學習帶來的湧現能力除了令人興奮之外，更帶來許多迷茫。或許，Marr的三階層分析除了能帶給腦神經科學及生物學指引，也能替機器學習提供新的靈感。

生命世界中湧現與承載的計算與演算法

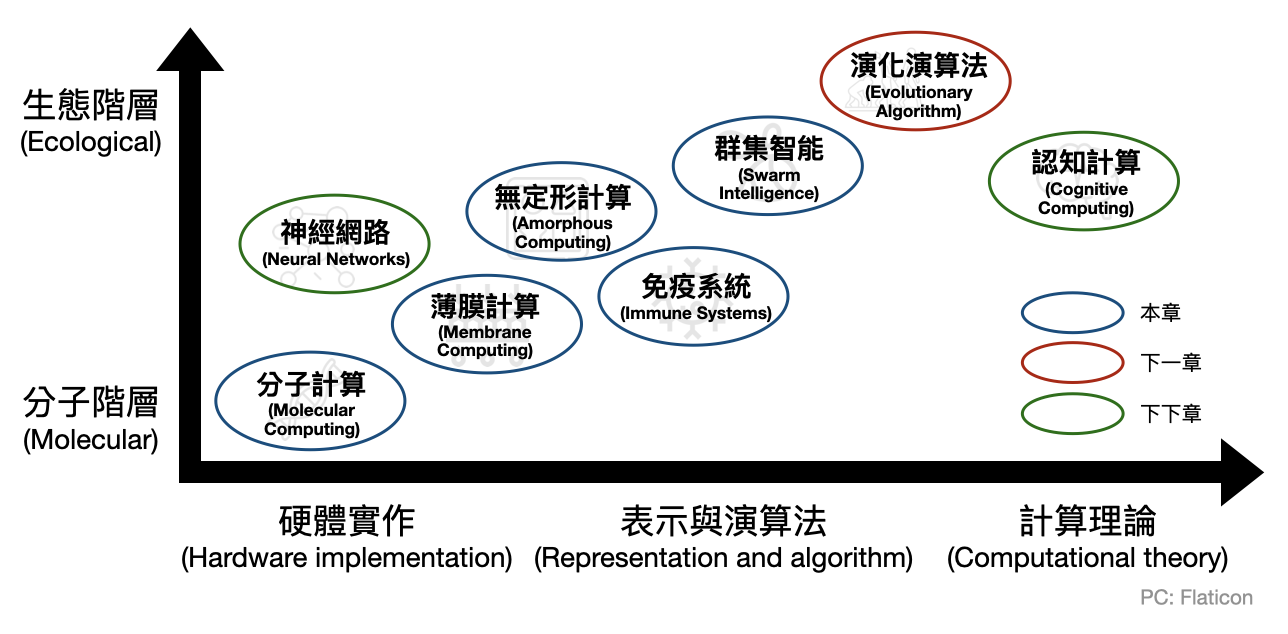
在經歷了一些嚴肅的哲學性思考和討論後，我們終於準備好觀賞計算是如何在生命世界中不同的層次湧現。受限於篇幅，本書將只提供八個例子：分子計算、薄膜計算、免疫系統、無定形計算、群集智能、演化演算法、神經網路與認知計算。感興趣的讀者，歡迎參閱延伸閱讀。

在本章剩餘的篇幅中，我們將一覽前五個例子。演化和腦神經科學相關的主題將會在接下來兩個章節中有更詳細的討論。

分子計算

RSA密碼系統是目前最普及的公共密鑰加密系統，三位發明人也一起在2002年獲得了理論電腦科學屆最高榮譽的圖靈獎(Turing award)。RSA密碼系統中的“A”是Leonard Adleman，除了這項重要的貢獻之外，Adleman另外也因為開創了DNA計算(DNA computing)而著名。

核鹼基(Nucleobase)以及兩兩配對後形成的鹼基對(base pair)是生物世界中最底層的文字，其扮演的角色有點類似現代電腦中的電晶體，兩者不但大小相似，也都是用離散的(四元和二元)方式儲存訊息。不過，兩者最大的差別在於能量的來源：核鹼基和鹼基對的反應主要使用諸如氫鍵等等的化學能，電晶體則是使用電力。再加上後者需要被固定在特殊的結構上，這使得前者的運作相對省了不少能源。於是，Adleman便突發奇想，能否用核鹼基和鹼基對來實現新的電腦架構！？

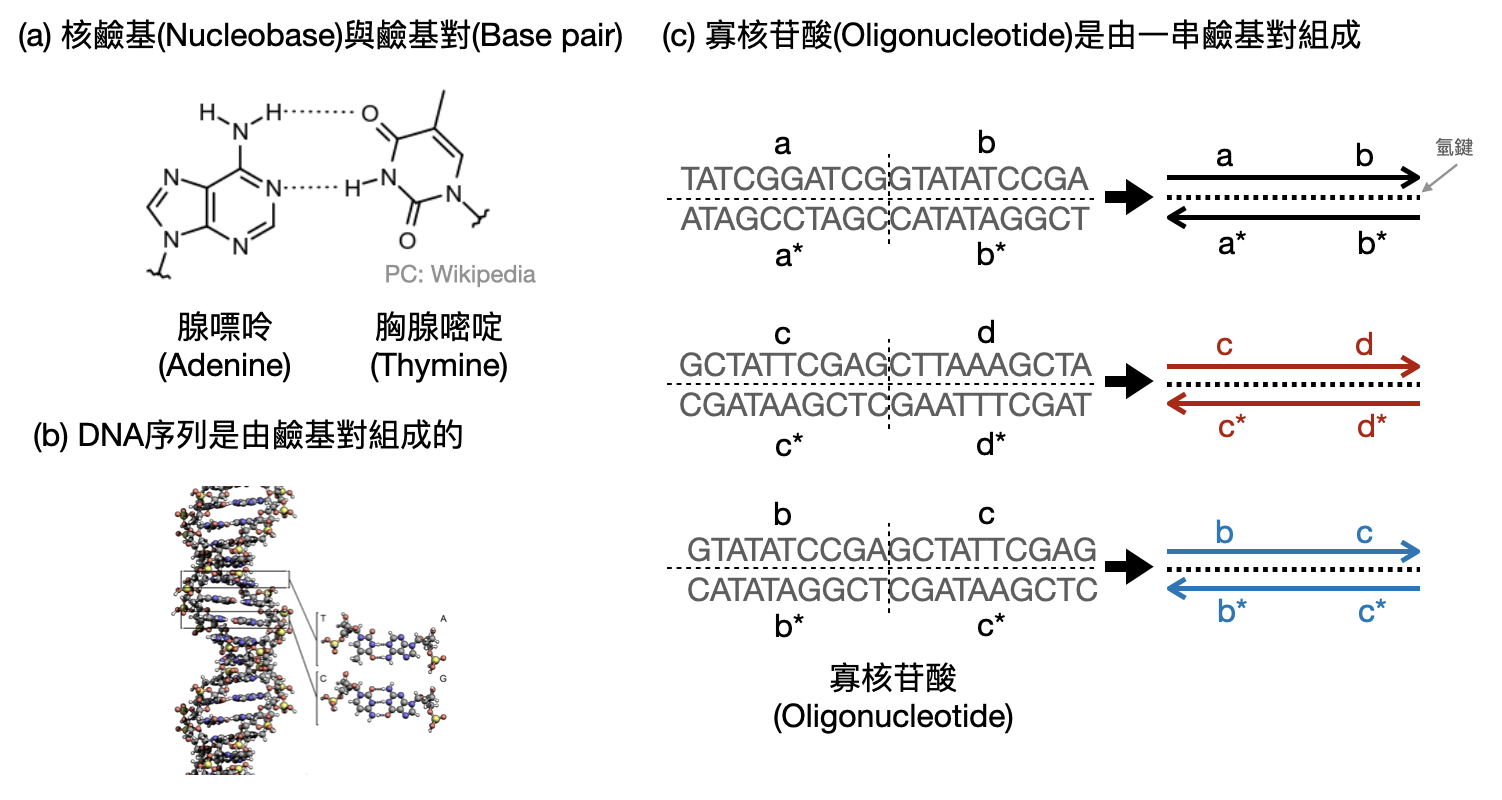
在看看Adleman是如何實現其想法前，讓我們先補充一些生物知識。如同英文單字是由許多字母的排列組合形成文字，電腦語言是由0/1的排列組合形成數值與指令，在DNA中核鹼基會用不同的排列組合連接形成長度大約為10~20左右的寡核苷酸(Oligonucleotide)，如此一來生物世界底層的單詞就出現了(如下圖(a))！每種核鹼基會和另外一種核鹼基被氫鍵連接起來(A和T、G和C)，於是一個寡核苷酸將會有個對偶的寡核苷酸(如下圖(a))。最後，當生物體真正在使用DNA時，將只會關注由寡核苷酸組成的單詞而非單一核鹼基的符號。因此，我們可以更進一步將一條DNA抽象為一串寡核苷酸組成的文章(如下圖(b))。

(a)核鹼基(Nucleobase)是DNA和RNA最基礎的符號。核鹼基會兩兩透過氫鍵依照A和T、G和C的規則結合。(b)成對的核鹼基會相連成串，形成雙股螺旋狀的DNA。(c)DNA中的核鹼基對並不是隨機排列的，通常有些長度約10~20的核鹼基對排列組合會不斷出現，因此這一串核鹼基對會被對應到一個寡核苷酸，並且會被抽象化為一個符號。在本圖中，TATCGGATCG被稱為a，其對偶的ATAGCCTAGC則被對應到a*。在之後的討論都將會只關注在寡核苷酸這個層次的編碼方式。

生物體是如何利用DNA這樣奇妙的機制建造出複雜的結構呢？這遠遠超出了本書的範圍，目前在研究前端仍充滿許多未解之謎。Adleman並沒有要試著模仿生物體使用DNA的方法，而是想試試看能不能用這樣現成的機制，來承載來自人工世界的計算。在他1994年著名的論文『Molecular computation of solutions to combinatorial problems』中，他設計了一個基於DNA機制來解「有向Hamiltonian路徑問題(Direction Hamiltonian path problems)」的演算法！

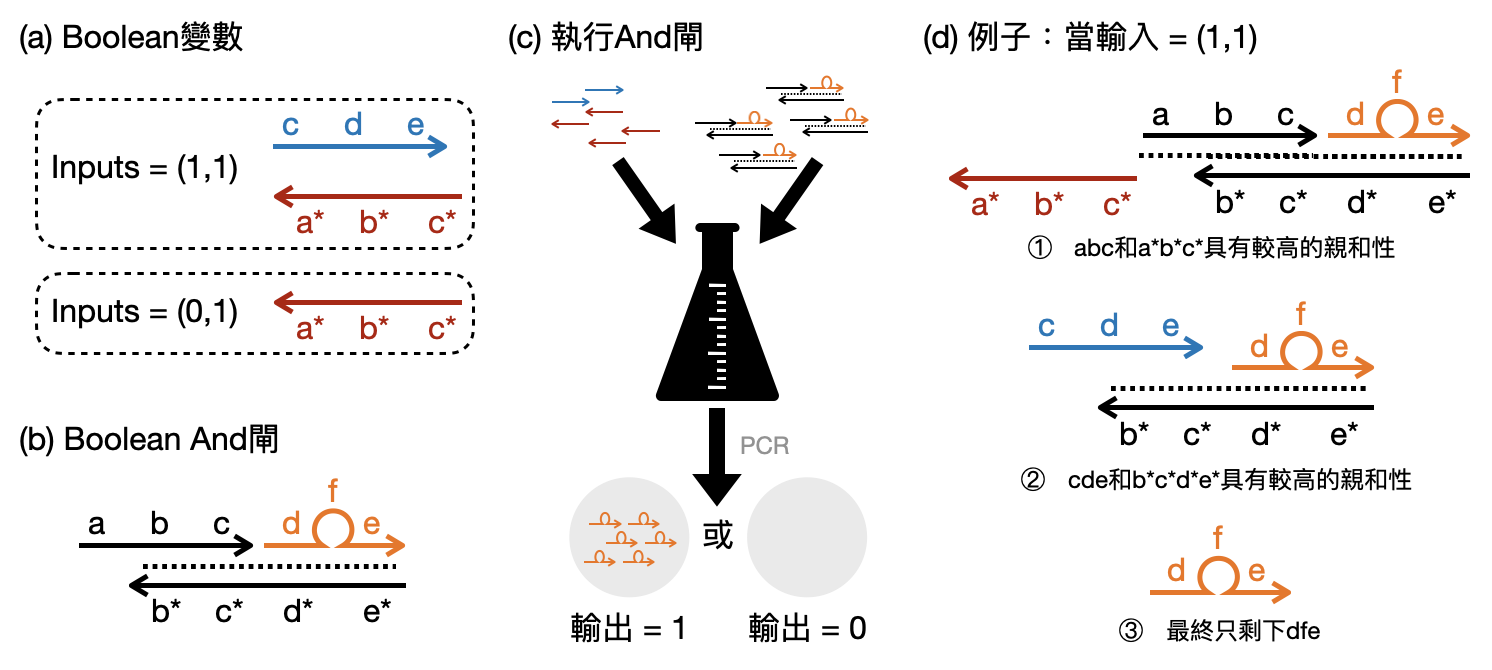
在這邊讓我們用個簡單的例子，看看如何使用上述的DNA機制來實現一個Bolean邏輯中的“和(AND)”運算。

(a)在DNA計算中，一個Boolean變數對應到一段寡核苷酸是否出現。例如本圖中有兩個Boolean變數分別對應到寡核苷酸cde和a* b* c* 。當這兩個變數取值都為1時，兩種相對應的寡核苷酸都會出現。而當只有第二個變數取值為1時，就只有 a* b* c*會出現。(b)一個Bolean邏輯中的“And閘”可以透過圖中的分子實現。(c)在執行這個And閘時，會將變數對應到的寡核苷酸以及And閘的分子混合到一個溶液中進行反應。接著透過PCR(polymerase chain reaction, 聚合酶鏈反應)將剩餘的分子數量放大，根據是否有dfe寡核苷酸來判斷結果是0還是1。(d)以輸入為(1,1)的情況為例，寡核苷酸a* b* c* 和cde都會出現在溶液中。由於a* b* c*和And閘中的abc具有更大的化學親和力，於是會將And閘分子的abc部分搶走。接著，由於cde和甚於的c* d* e*具有更大的化學親和力，And閘將只會剩下dfe，也就是說最終對應到的變數取值為1。

感興趣的讀者可以想想看該如何用類似的方法實現Bolean邏輯中的“逆(negation)”運算，一旦做到了，DNA計算就會是圖靈完備(Turing-complete)了(忘記相關定義的讀者請參考本書第二章)！

薄膜計算/細胞計算

成年人體內約有30幾兆個細胞，常見的種類就至少有兩百種。我們體內每天都有如此巨量的細胞在活動，勢必也有些“計算”在進行，該如何建立一套語言來描述細胞的奇幻世界呢？

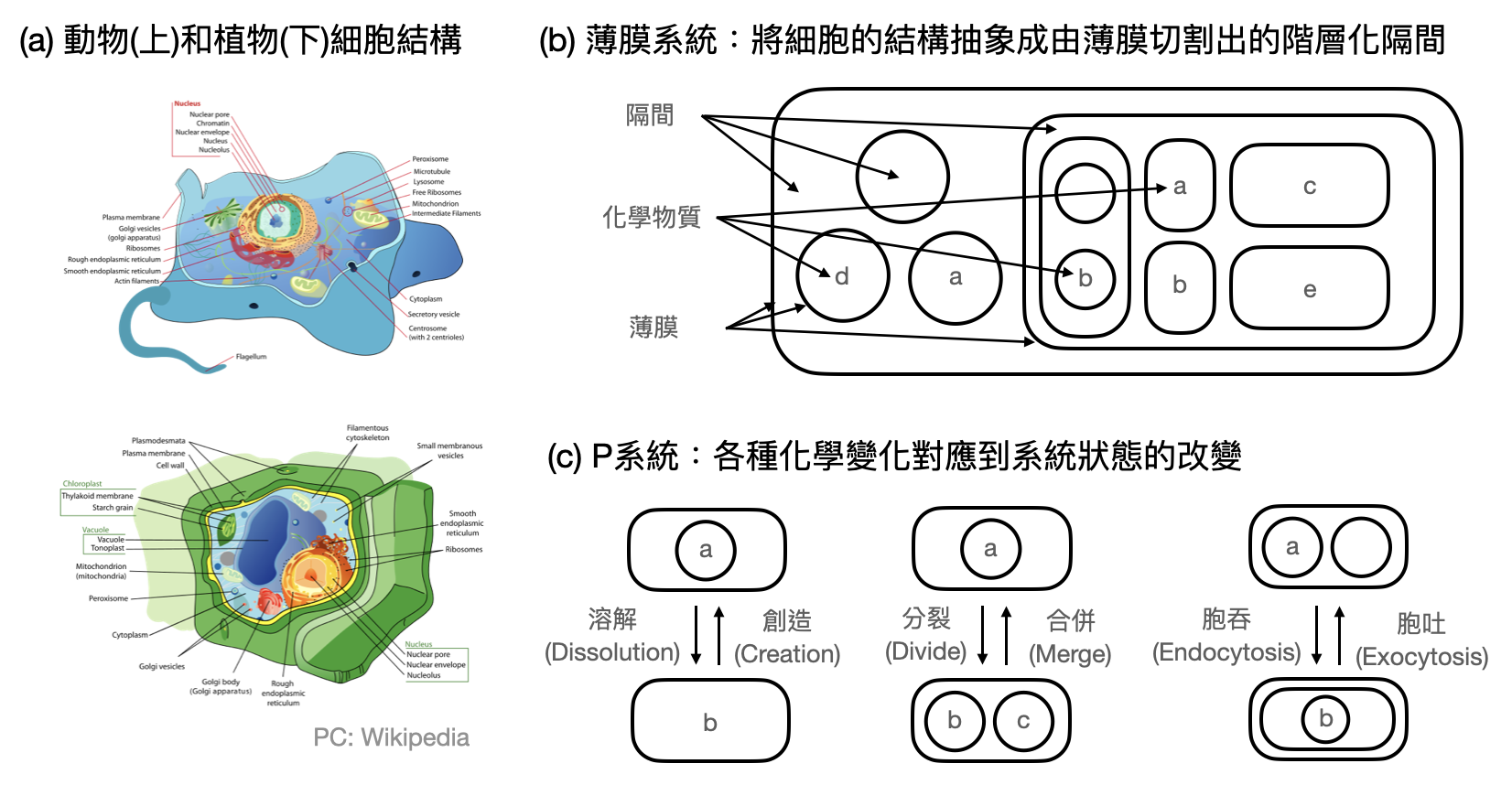
在中學生物課中，我們會學到動物細胞有細胞膜、細胞質、粒線體、液胞、細胞核等子結構，植物細胞則多了葉綠體、細胞壁。對真正的細胞來說，並不是見得會完全照著這兩種大框架，而是會有些許的增減。如果抽離出許多生物的細節，抽象上來看細胞是由許多薄膜(membranes)區分出許多隔間(compartments)的「薄膜系統(membrane systems)」(有時候又被稱為P系統)。一個薄膜系統在某個時刻的狀態，在形式上完全由隔間的相對關係和之中包含的化學物質所描述。不同的薄膜會允許不同的化學分子出入，隔間也可能會在不同的化學反應之下分裂或合成。這些“演化規則”(如下圖(c))會改變薄膜系統的狀態。

於是，薄膜系統就很自然地對應到一個計算系統了：狀態對應到訊息(輸入、輸出、或計算過程)的編碼，演化規則對應到訊息的處理。一旦能夠調控好輸入狀態是如何對應到輸出的狀態，那麼就可以駕馭薄膜系統，利用它來幫忙做計算了！

你能試著說明/證明為什麼薄膜系統是圖靈完備的嗎？你覺得它是個好用的計算模型嗎？

(a)教科書中動物細胞(上方)與植物細胞(下方)的結構圖。(b)薄膜系統，又因為其發明人是Gheorghe Păun而被稱為P系統。一個薄膜系統的狀態可以被隔間之間相對關係與之中包含的化學物質所描述。(c)薄膜系統中的狀態會透過幾個演化規則做轉換，例如圖中的溶解/創造、分裂/合併、胞吐/胞吞等。透過利用狀態來編碼資訊，演化規則就成為了可以使用的計算步驟。

無定形計算

你是否曾經想過，一個人到底如何從一個胚胎細胞，透過不斷的細胞分裂，最終分化出各式各樣的細胞、組織和器官？難道只要把初始狀況設定好(例如DNA)，夠透過不斷重複相同的演化規則，甚至是在極度平行化和沒有中央控制的情況下，就能產生出複雜且多變的結果？

無定形計算(Amorphous computing)就是想要來刻畫這樣的計算方式。不過以胚胎發展學作為起始目標可能有點太困難了，另一個生物世界中常見的例子是動物身上的花紋。無論是絢爛的熱帶魚花紋，還是精緻的豹紋，任何人看了都會讚嘆大自然的巧妙。到底是什麼樣子的化學/生物反應，能夠達成如此既富有規則又多變的花樣呢？是需要一筆一筆地精雕細琢，還是只要不斷重複一些簡單且無定序的化學/生物反應就可以做到了？。

(a)胚胎的發展是由簡單、重複、且不同步的過程組成，然而其結果可以非常的複雜且具有結構。(b)動物的花紋同樣具有類似'無定形計算'的特徵。Turing曾經提出用兩種化學物質的反應擴散模型(reaction-diffusion model)來產生類似豹紋的圖案，後世稱之為Turing圖案。

電腦科學的祖師爺Turing也曾經思考過這個問題，並且在一篇著名的論文『The Chemical Basis of Morphogenesis』中提出如何透過兩種化學物質之間的反應(reaction)和擴散(diffusion)，就可以產生如豹紋般眩目的花樣(如上圖(b)的下方三圖)。為了紀念Turing開創性的發現，人們又將這種透過簡單反應生成的複雜圖案稱為Turing圖案(Turing pattern)。

無定形計算位於生物、物理、化學、數學等學科的交界之處，在複雜與結構交織湧現但細節尚未失去重要性之際，我們該如何揭開這一層計算的面紗？

免疫系統

近幾年來，新冠病毒的疫情讓世人重新認識免疫系統的重要性。同時，日益猖獗的網路駭客攻擊也警惕著我們要更加注重資訊安全。這兩者難道有什麼相似的地方？

免疫系統的關鍵在於如何正確區分外來的敵人細胞/病毒和自身的友好細胞，而資安系統的任務則是在功能和服務正常運作的情況下，辨別並阻擋惡意的攻擊程式。這樣一看，兩者是不是有著異曲同工之妙？

如果更深入學習免疫系統，會發現裡面具有許多很有巧思的演算法設計概念！為了能迅速讓讀者感受到免疫系統和資安的關聯，以下我們將著重在後天性免疫(adaptive immunity)中的免疫寬容(immune tolerance)。感興趣知道更多的讀者歡迎參考延伸閱讀。

當外來病菌已經突破了皮膚以及先天性免疫的這兩道免疫防線之後，後天性免疫就準備要啟動更全面性的防衛了。後天性免疫很講究專一性(specificity)，如此一來才能夠精準地打擊敵人。不過此時困難的地方就出現了，世界上的病菌這麼多，免疫系統該如何迅速地瞄準目標攻擊，甚至是記住曾經出現過的病菌？同時，身體內的細胞也是千百種，該如何防止不小心錯傷自己人？

如此不錯傷自己人的功能，又被稱為免疫寬容(immune tolerance)。在人體的免疫系統中，有許多機制合力朝免疫寬容的目標前進。在介紹幾種常見和重要的機制之前，必須先強調一下生物界的免疫機制並不是完美的，這些機制再怎麼厲害，都還是有可能在某些情況下失敗。所以在欣賞這些精巧的設計時，雖然可以用演算法的角度去理解，但是要謹記這和數學世界中能夠證明對所有情況都成功的演算法很不一樣。

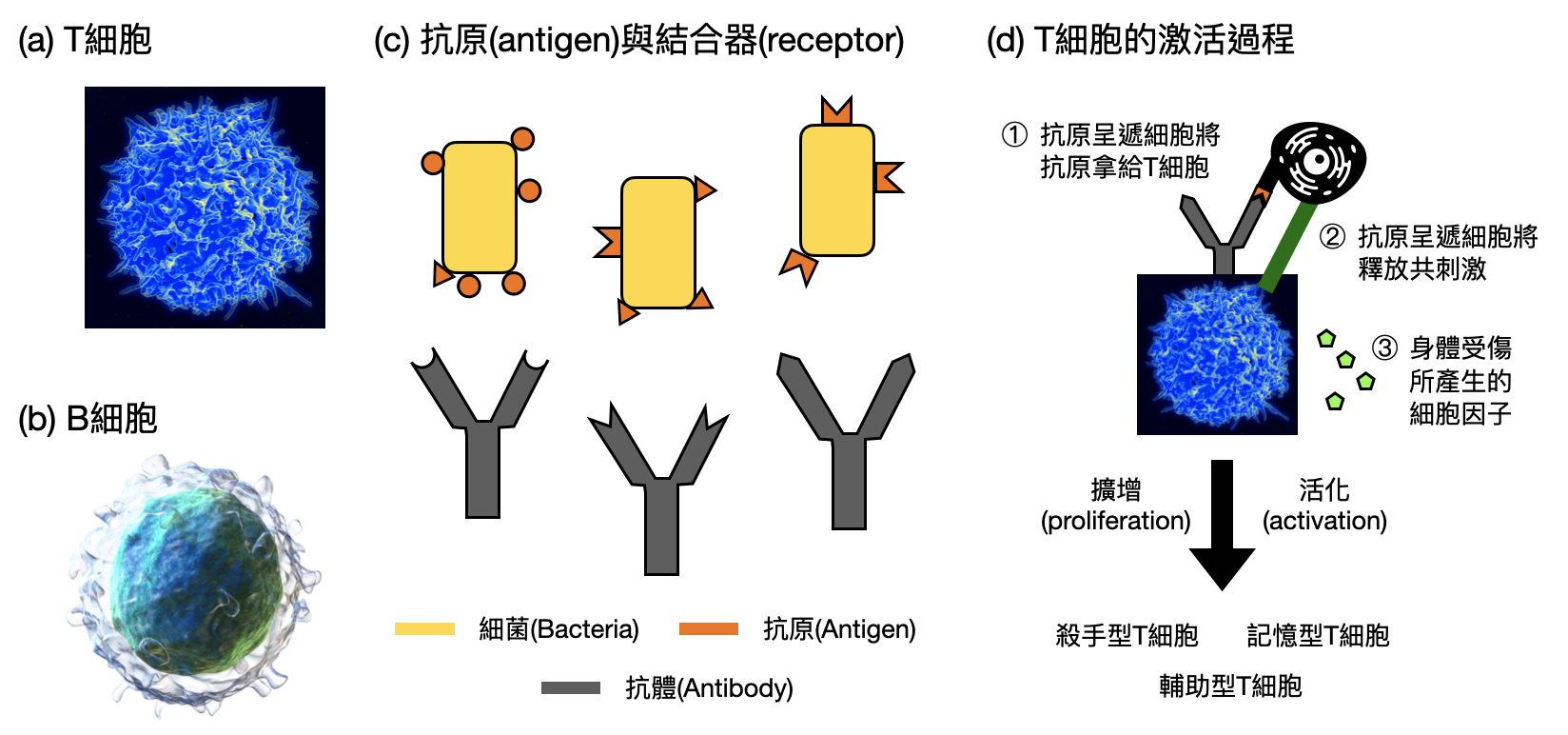
(a)T細胞。(b)B細胞(c)細菌身上會帶有各式各樣的抗原，根據不同的基因訊號，抗原長的樣子會很不一樣。同時，T細胞和B細胞的表面會有許多結合器，一個T細胞/B細胞可以識別一種抗原。由於骨髓會產生大量具有不同抗原結合器的T細胞和B細胞，任何的抗原基本上一定都會有相對應的結合器出現在體中。(d)T細胞的激活過程有三步，需要同時達成才會活化後續的連鎖反應。

後天性免疫主要有B細胞和T細胞這兩種主力戰將，它們都是淋巴細胞的一種，並且在表面會有和特定抗原(antigen, COVID快篩試劑就是用它來判斷是否中鏢)結合的結合器(receptor)。一旦B細胞或T細胞和某種抗原結合之後，就有可能開啟一連串的連鎖反應，例如開始大量增殖(proliferation)、變身為作用/輔助型T細胞(effector cell)、變身為記憶B細胞(memory cell)等等。每個B細胞和T細胞的表面都有成千上萬個結合器，而且對同一個細胞來說，所有的結合器都是對同樣的抗原有反應。骨髓會產生大量對不同抗原有反應的B細胞和T細胞，使得在之後有外來入侵者時，基本上都必定會有些B細胞和T細胞能夠抓住相對應的抗原。但同時，骨髓也無法控制讓B細胞和T細胞的結合器不會對自身細胞產生的抗原有反應(auto-reactive/self-reactive)。因此，免疫寬容的重點就是要正確辨識和B細胞與T細胞結合的抗原到底是敵是友，如此一來才能正確地開啟連鎖反應(或是在苗頭不對時趕快踩煞車)。

為了避免讓剩餘的篇幅不會變成像是在上免疫學課，在這邊我們主要只專注在T細胞的免疫寬容。

中央免疫寬容(Central tolerance) 指的是淋巴細胞在尚未正式進入循環工作前進行的免疫寬容機制。被骨髓(bone marrow)製造之後，T細胞接著會移動到胸腺(thymus)發展成熟，並確定了表面抗原結合器的型態。接者，這些T細胞會經過為期數日的審核過程，在這段期間內，會有大量在表面持有來自人體其他處抗原(正確來說，只有多肽的抗原)的MHC(major histocompatibility complex; MHC; 主要組織相容性複合物)，到處移動看看是否會和哪個T細胞反應。如果一個T細胞都沒有和任何MHC反應的話，那麼它就會慢慢死掉。這又被稱為正向篩選(positive selection)，因為這些沒有反應的T細胞在真正開始工作後很大的機會也不會派上用場，不如早點淘汰。

然而如果某個T細胞和一個MHC結合得過度緊密，那麼它也會死掉。這又被稱為負向篩選(negative selection)，主要目的就是避免在未來會不小心被自身的抗原觸發免疫系統的連鎖反應。

周邊免疫寬容(Peripheral tolerance) 指的是當淋巴細胞進入身體循環後，如何避免被自身的抗原激起免疫系統的連鎖反應。當T細胞表面的結合器和抗原媒合成功之後，並不會立即啟動免疫系統的連鎖反應，而還需要另外兩個條件：(i)共刺激(co-stimulation)和(ii)細胞因子(cytokine)。抗原呈遞細胞(antigen-presenting cell, APC)會將抗原拿給T細胞看，並且釋放共刺激，其扮演的角色類似於槍上的插銷，可以防止T細胞們一不小心碰到一個抗原就擦槍走火。細胞因子則是當身體有傷口時，會自動釋放的訊號，其扮演著類似於警報系統的角色，假想看看如果沒聽到警報但在轉角看到一抹黑影，可能很高的機會只是隻老鼠而非入侵的敵人。

看了這些免疫寬容的例子，不妨可以想想看這些機制的優缺點為何，你能想出更好的機制嗎？

群集智能

俗話說三個臭皮匠勝過一個諸葛亮，那如果是一百隻鳥、一千隻螞蟻或一萬隻黏菌呢？它們會比人類還聰明嗎！？

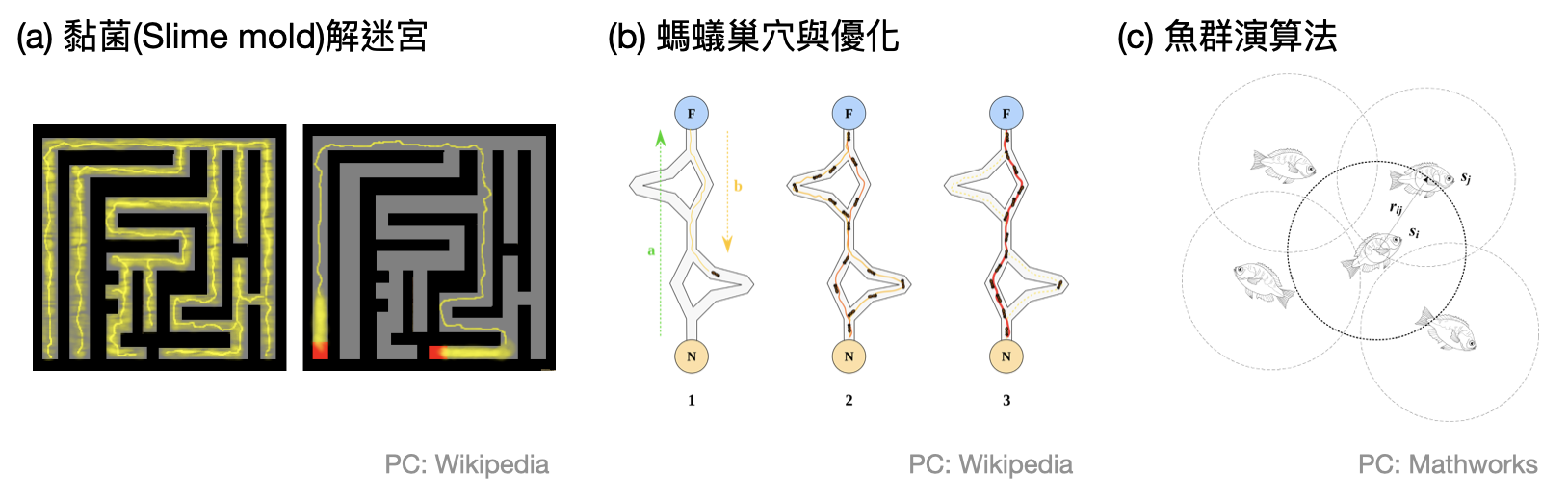
當然，如果是在講整體的智能，那麼一個人的確應該能完勝一大群非人生物。不過如果是針對特定的計算問題呢？一群看似沒有很聰明的生物，有沒有辦法集體展現令人折服的計算能力呢？這就是群集智能(Swarm intelligence)想要探討的計算方法，下圖提供了三個常見的例子。

(a)科學家在一個迷宮的起點與終點放上食物，並將整個迷宮填滿黏菌(圖中黃色的東西)。在實驗中，經過一段時間後黏菌們會漸漸收斂到一條連接起點與終點的最短路徑。(b)螞蟻也有展現類似黏菌解謎宮的能力。一群工蟻從巢穴(圖中下方的N)出發尋找食物時，一開始會分批往不同的方向探索，當找到食物後(圖中上方的F)，工蟻們會漸漸捨去較遠的路徑，只停留在食物與巢穴之間的最短路徑中。(c)大海中的魚群，或是空中的鳥群，在集體運動時可以維持差不多的間距，朝著相同的方向移動，並自如地轉彎。

當一大群舞者在廣場跳舞時，和諧同步的動作是透過經年累月的訓練累積下來的。然而如上圖(c)中的魚群或是空中的鳥群，它們卻似乎天生(或是沒有經過多少訓練)就能自如地成群移動。更厲害的是，當遇到風向或是海流的瞬間變化，它們通常都能即時的反應，你可曾經看過飛鳥不小心撞到對方？

在這些群集智能的例子中，也許不像前面的例子有明顯可以對應到的計算模型或是計算問題。其所涵括的計算層面是在於個體如何透過有限的局部資訊(例如鳥兒只能看到附近的同伴，以及身邊的風向)，快速計算出下一個瞬間應該採取的行動。

如果你會寫程式的話，不妨想想看如何寫個程式讓“機器魚”也可以達到類似的能力？如果不會寫程式的話沒關係，可以想想看在大型聚會發生緊急狀況時，該如何在沒有中央指揮的情況下，讓人們平安轉移陣地脫離險境？

總結

從DNA編碼生命的秘密，到演化帶來的多變世界，只要細心觀察，總是可以在每個角落發現大自然巧妙設計中的驚喜。在這個精彩的藝廊裡，計算不但幫助研究者更有效率和更深入地探索，也提供了一個不一樣的視角來理解許多性質與現象。

在本章中，作為開胃菜我們淺嚐了五道生命世界中湧現與承載的計算和演算法。在接下來的兩個章節，我們將分別專注於演化及腦神經科學這兩道主菜。也許現在你會納悶為什麼是這兩個子領域呢？希望在讀完之後，你能從其中豐富的思想縱深共鳴主廚背後的巧思。

延伸閱讀

內文引用的論文：