$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



第9章

萬物更迭背後的齒輪：演化論





Evolution has no long-term goal. There is no long-distance target, no final perfection to serve as a criterion for selection.

演化中沒有長遠目標、沒有遠距離目的、也沒有終極完美作為選擇的基準。

Richard Dawkins


在上一章我們認識了許多生命世界中與計算意想不到的連結，從微小的DNA、細胞的薄膜、免疫系統到群集的動物，這些豐富的結構可都要感謝大自然億萬年的精雕細琢。同時，這個從無到有的“演化”過程，更是可以被視為一個巨大的“計算過程”，讓我們有機會來透過計算的視角研究。演化除了賜予我們多采多姿的家園，是否還有更多深層的奧秘等待我們挖掘？

達爾文的天擇論與物種的起源

「物競天擇」，是身在二十和二十一世紀的我們，從小耳濡目染並朗朗上口的概念。也許記憶中依稀記得這和達爾文用來解釋物種的起源有關，更多時候我們則是將其(不恰當地)應用在社會上與他人的競爭中。這個看似簡單，甚至有點理所當然的想法，為什麼會讓達爾文擠身十九世紀偉大科學家的行列呢？生物是怎麼競爭的，“天”又是怎麼選擇的？為什麼在這樣的世代循環之下，就會讓不同物種自然湧現？這一切又和計算有什麼關聯！？

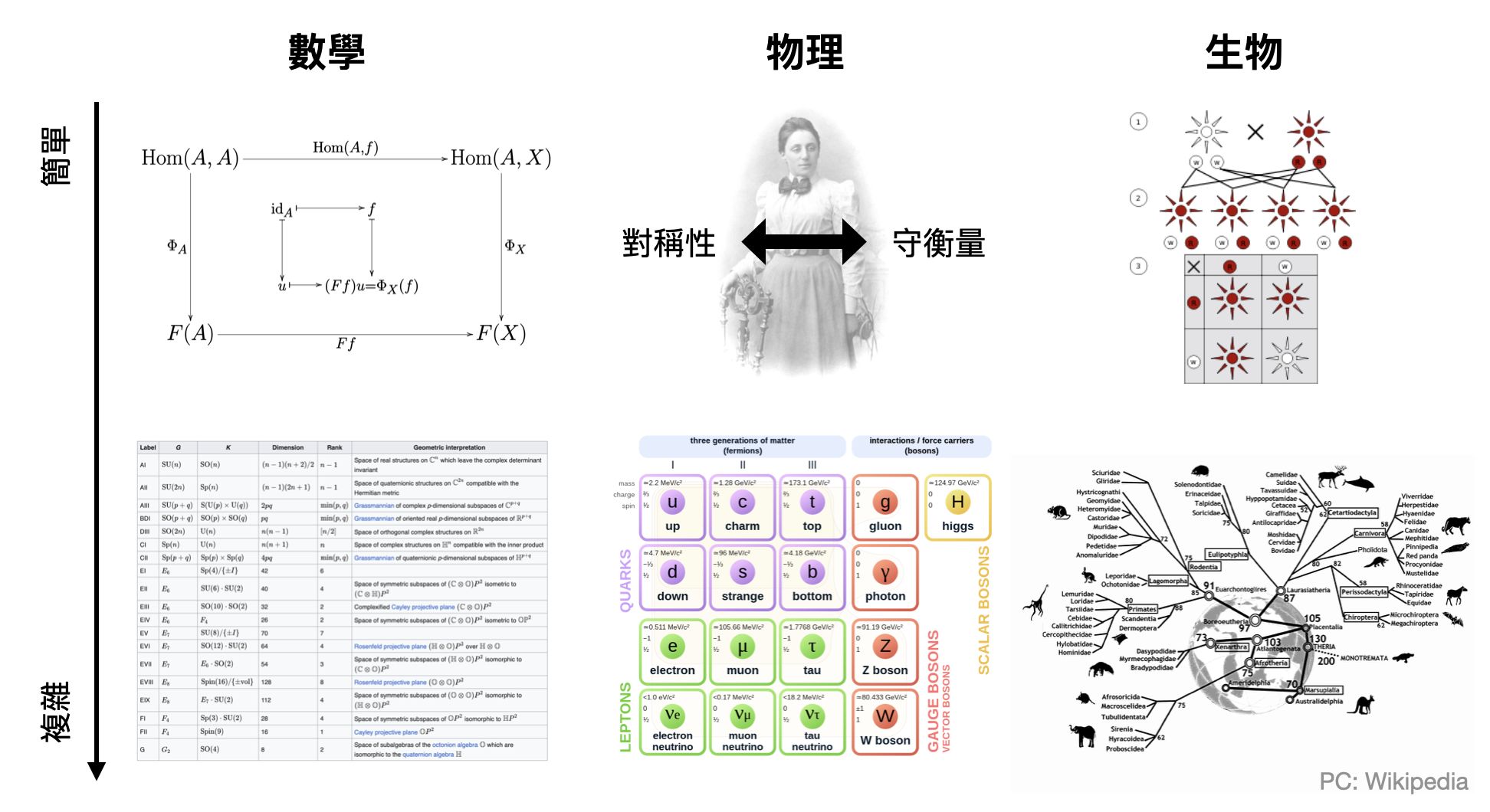
結構與隨機性

筆者從小生長於理工背景的家庭，一直到讀博士初期都還不太能欣賞所謂生命世界中的多樣性。出外踏青時對於花花草草沒有太多特別的感覺，看到家裡沙發上突然出現的蟻后只會落荒而逃，不像專攻演化生物學的室友會開心地拿出試管，購入螞蟻專用飼養盒，然後在書桌上建起小型螞蟻生態圈。從小到大，除了運動之外，就是抽象思考能夠帶給我精神上的糧食，徜徉在數學世界中精妙的結構，讚嘆於物理的乾淨與對稱。反觀生物和歷史是高中時讓我最頭疼的兩門科目，其中後者還成功地讓我念不到物理系…那為什麼生命世界佔了這本書的三分之一呢？是什麼讓我在近幾年漸漸地開始會留心於幾片樹葉的異同？為什麼在多年後重新拜訪台中的自然科學博物館時，對這些從小看到大的展覽有了煥然一新的感受？

對我來說，這些對生命世界的感動，和在數學中體會到的非常相似，都是源於結構的美。

第一次在範疇論(category theory)中看到Yoneda引裡時，被那種既糾結又乾淨的視角所震撼。在路上等火雞過馬路時，思忖著生命如何從DNA與蛋白質湧現出秩序。不管是在數學、物理、還是生命的世界中，結構都是無所不在的，只差有沒有注意到而已。將結構形式化後，不但成為科學研究的基石，更是譜出一曲動聽的賦格。

(左上)範疇論中的Yoneda引裡。(左下)Élie Cartan對黎曼對稱空間(Riemannian symmetric spaces)的分類，圖中僅呈現分類的一部份。(中上)Noether定理。(中下)基本粒子的標準模型。(右上)孟德爾定律。(右下)動物界中簡化的親緣關係樹。

當然，數學、物理學和生物學尚不能混為一談，各自關注課題與方法論的不同，也造就了知識世界的多樣性。而在生物學中，結構之所以這麼不容易被揭發，主要源自於內蘊的隨機性。

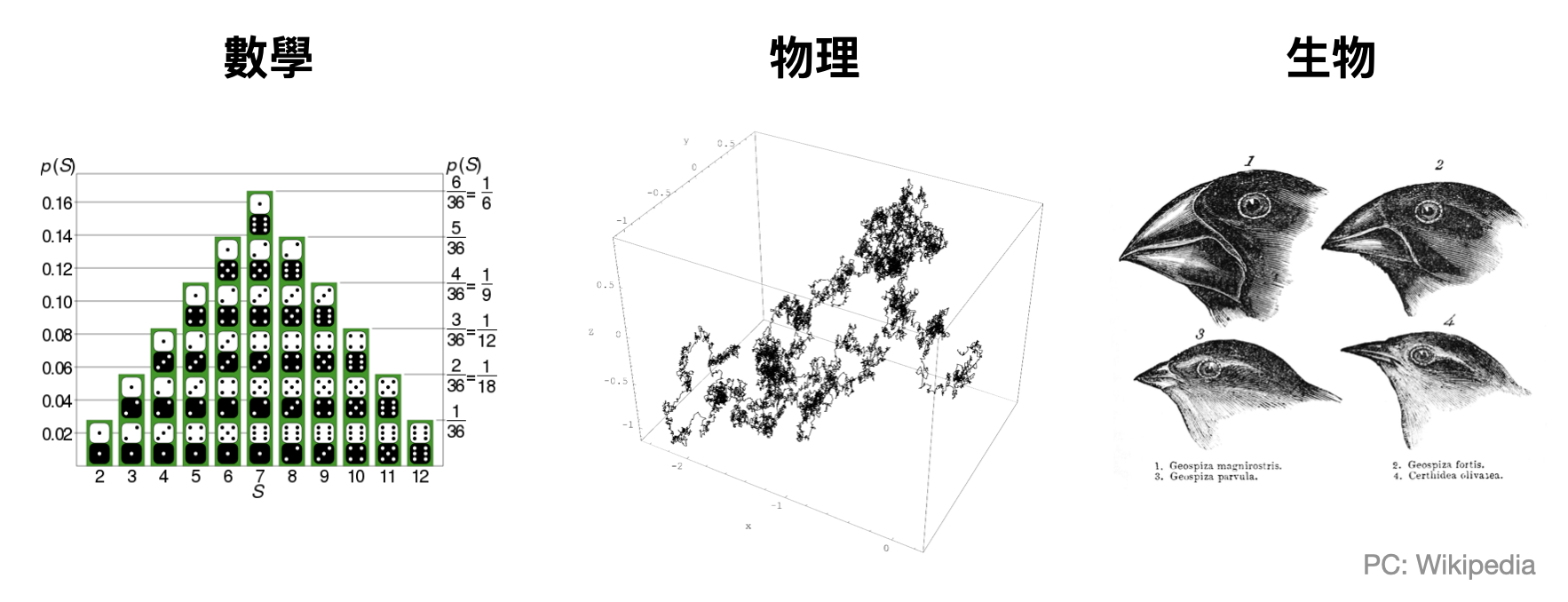
一提到隨機性就要小心點了。在數學和物理中對於隨機一詞有很特定的定義或理解，讀過本書前兩部分後讀者們或許已經能約略體會到。將數學和物理中的隨機概念搬移到生物學中必須非常謹慎。太多看似隨機的事物與現象，背後其實具有某些待發現的結構。隨機背後的湧現機制，也不見得能夠被簡單的數學模型刻畫。還記得筆者曾經在演化生物學家David Haig的課堂中，非常認真地試圖解釋量子物理和統計物理中對機率不一樣的定義，並且追問到底他們口中基因的隨機突變到底是屬於哪一種。現在想想，當時的我還真是完全弄錯Haig教授在討論中想要強調的重點，實在非常慚愧。

(左)機率論中的骰子。(中)用來描繪粒子在液體或氣體中隨機移動的布朗運動(Brownian motion)。(右)達爾文雀(Darwin's finches)，在加拉巴哥群島生活的幾種可雜交且體型近似的雀，但是其雀喙略有不同。

也許這也正是為什麼在生物學中，“分類學(taxonomy)”扮演著不可或缺的角色。例如，上圖中最右的達爾文雀們，它們屬於同一個物種嗎？透過由上而下梳理交織的結構與隨機性，建立一套語言承載形式化的理解。演化與天擇論，同樣也是一套形式化的語言幫助人們釐清模糊的直覺，勾勒出基礎輪廓，替知識的建構搬磚添瓦。

達爾文之前

就像牛頓不是第一個思考物理世界背後運轉機制的人，達爾文也非歷史上第一個嘗試解釋物種起源的人。早在古希臘時期，許多哲學家就已經嘗試建構世界起源的理論，而生物多樣性當然不會落在討論之外。

以亞里斯多德為例，他注意到了物種是個“動態”的概念，也就是說物種是可以滅絕與誕生的。以鳥類為例，他指出許多器官都是為了適應棲地而在外型或是功能上產生差異。亞里斯多德更進一步將生物中許多的結構抽象為「型式(form)」，並且在之上進行功能的討論與類比。對他來說，型式是要有用的，大自然不會用多餘的能量產生沒用的器官。

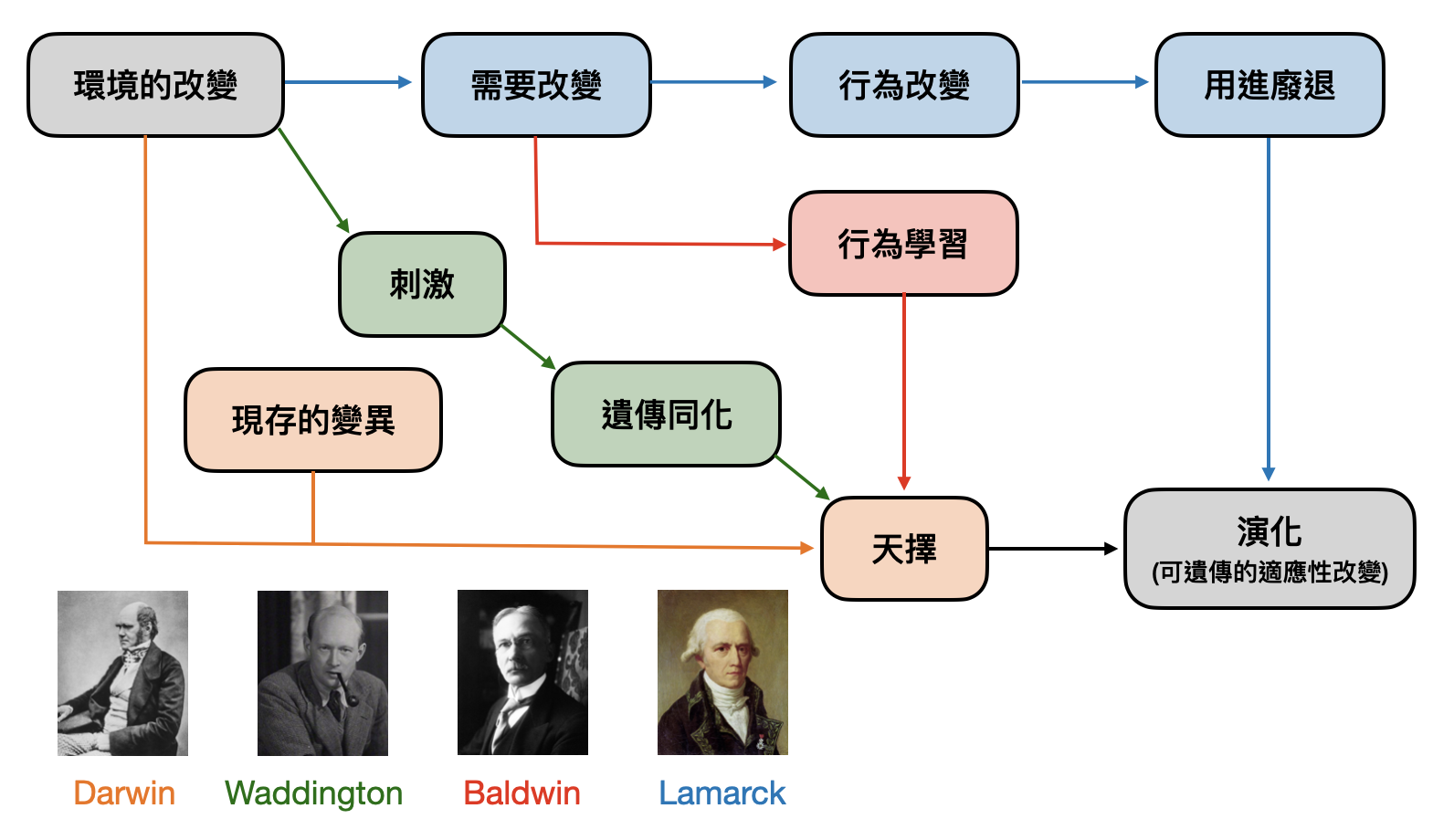
由下到上分別為達爾文的天擇論、Conrad Waddington(1905-1975)的遺傳同化論、James Mark Baldwin(1861-1934)的Baldwin效應、和Lamarck的獲得性遺傳與用進廢退論。隨著分子生物科學的興起，許多理論也有了新的詮釋和解讀。

到了中世紀及科學革命時期，重要的思想家與科學家如笛卡爾、牛頓等人，也沒有在物種起源與多樣性的討論中缺席。在18與19世紀交界之時，生物學家Jean-Baptiste Lamarck(1744-1825)提出的「獲得性遺傳(inheritane of acuired characteristics)」和「用進廢退(use and disuse)」概念盛極一時，其中心思想可以從簡單的例子中獲得：運動員身材練得很壯的話，他的小孩手臂應該也會很粗。如果Lamarck是對的，那麼人們是否會在生小孩子前更認真地鍛鍊身體和讀書呢？

同時，在科學研究的另一頭，人們試圖建立理論來解釋地球上地貌的成因與多樣性，山谷、冰河、盆地等等是如何出現的？例如Charles Lyell(1797-1875)在1830到1833年間發表的三卷『地質學原理(Principles of Geology)』，其中的「均變論(uniformitarianism)」強調緩慢而均質的變化為地質形成的關鍵，並首度嘗試論證地球的年齡遠比之前認知的六千年還要老非常多。

在這樣的時代背景之下，達爾文或多或少受到不同思想的啟發。不過他最終提出的天擇論，可能更多影響自他年輕時親身周遊世界的經歷。

從『小獵犬號航海記』到『物種的起源』

你二十歲的時候在做什麼呢？如果有人問你要不要加入一趟為期五年的航海探索之旅，你會答應嗎？1831年時值22歲剛剛畢業的達爾文，爽快地踏上了一趟改變他人生的旅程：「HMS小獵犬號的第二趟航行之旅(Second voyage of HMS Beagle)」。

在船上五年的時間中，達爾文也沒閒著，除了把Lyell的地質學原理仔細讀完，更是每天寫日記，紀錄航行中的所見所聞。並在旅程結束後將內容於1839年發表成書『小獵犬號航海記(The Voyage of the Beagle,)』，一時之間洛陽紙貴。

出版了第一本書之後，達爾文便開始醞釀如何解釋他一路上見識到的物種多樣性，早在1840年代就有紀錄提到他曾經和其他學者提過類似天擇論的概念。不過他一直不停地搜集更多證據，不斷地試圖將抽象的理論概念，套用在不同的物種及層面上。

(a)『物種的起源』(左)、達爾文(右)和HMS小獵犬號的第二趟航行之旅的路徑圖(下)。(b)『馬來群島』(左)、Wallace(右)和馬來群島在地圖上的位置(下)。

直到1858年，達爾文收到了Alfred Russel Wallace(1823-1913)的一封信，信中Wallace很有禮貌地和達爾文分享他對物種起源的看法，並請求達爾文提供意見。達爾文發現Wallace的理論基本上和他想的如出一轍，於是很有紳士風度地邀請Wallace將他們各自獨立發現的理論與觀察共同發表出來，盡快讓領域的其他人知道。於是，在Lyell和當時著名的植物學家Joseph Dalton Hooker(1817-1911)的牽線下，將兩人研究的摘要於1859年共同發表在倫敦林奈學會(Linnean Society of London)的期刊中。同年，達爾文也出版了其鉅作『物種的起源(On the Origin of Species)』。Wallace則是到了1869年才將其田野考察發表在著作『馬來群島(The Malay Archipelago)』中。

雖然在歷史的洪流中，大部分人都只記得達爾文是天擇論的提出者，但是從達爾文和Wallace的故事中，我們可以看到兩人都是累積了數十年田野間第一線的觀察經驗，大量搜集和比較不同的資料來支持理論的合理性。

讀了這麼多背景故事，現在我們終於準備好進入正題，品嚐天擇論的核心概念了！

天擇論的核心概念

Richard Dawkins是為當代有名且稍具爭議性的演化生物學家，除了其成名作『自私的基因(The Selfish Gene)』之外，另一本於1986出版的『盲眼鐘錶匠(The Blind Watchmaker)』也是極具影響力，其中貫穿全書的譬喻更是絕佳地展示了天擇論的核心概念。

就像經濟學家將市場類比成一雙看不見的手，Dawkins將演化中的天擇比喻成一位盲眼的鐘錶匠。盲眼是因為它並不能往未來看，無法提前規劃要做些什麼，更沒有個明確的目標。然而天擇的結果卻是如此的驚人，從DNA精準的編碼、蛋白質的轉譯、生物的發育到行為與智慧等等，如此精細的設計，堪比環環相扣的鐘錶。

除了用“物競天擇”簡單總結達爾文在天擇論中提出的主要機制，更具體來說還有以下三個核心原則指引著演化學家。

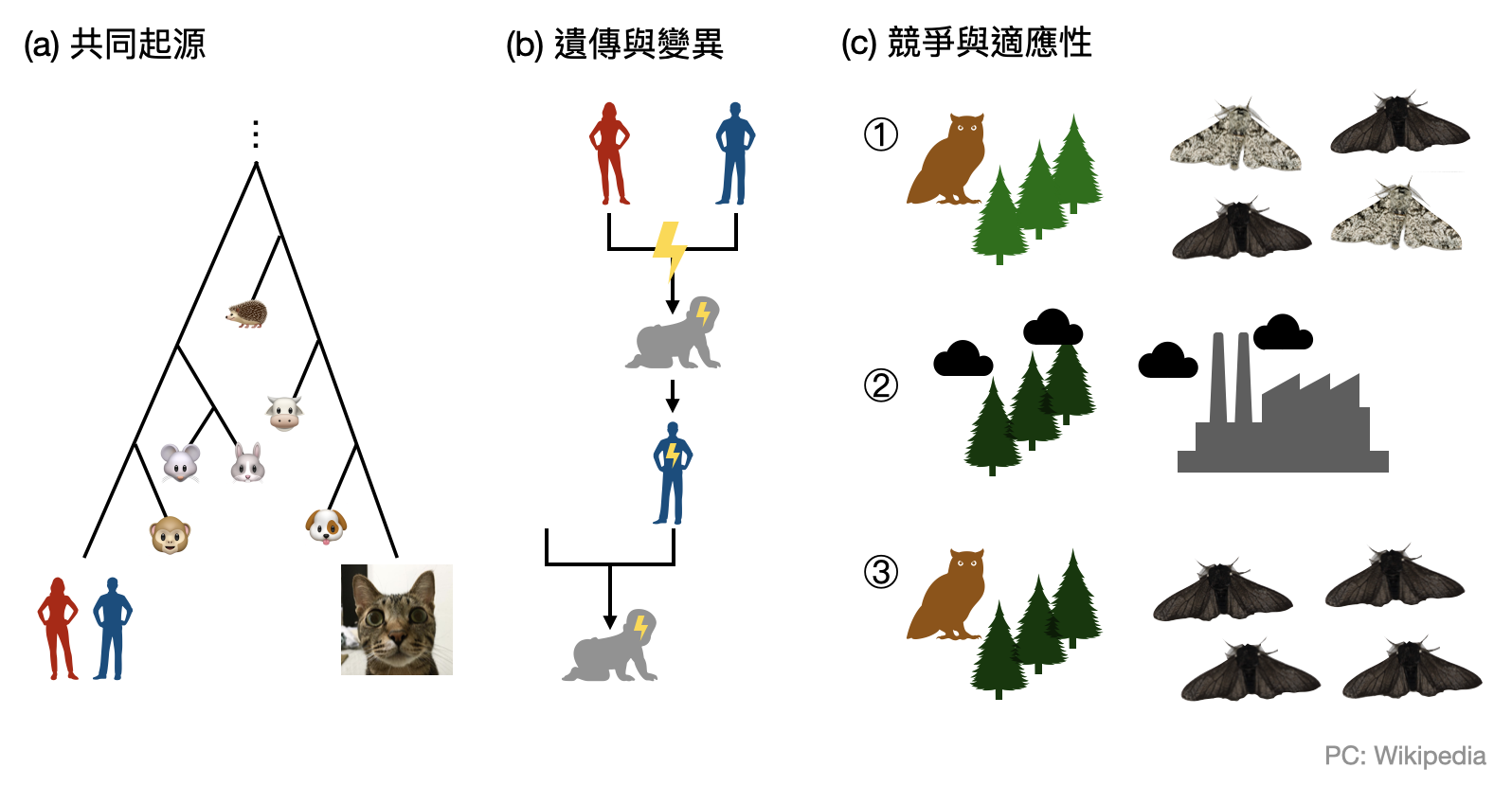
共同起源(Common descent)： 所有的生物都具有相同的祖先。演化的過程就像是一棵樹，雖然不斷有分叉，但任何兩個生物/物種都可以在這棵樹上找到交會的源頭。然而，該如何認識這棵樹呢？早期人們透過比較生物的外型(或是化石標本)相似度勾勒出演化樹的雛形，又被稱為「型態樹(morphological tree)」。隨著分子生物技術的起飛，則讓演化樹有了各種從基因序列定義出來的版本，通稱為「親緣關係樹(phylogenetic tree)」。

(a)共同起源：極度簡化版的親緣關係樹。(b)遺傳與變異的示意圖。(c)競爭與適應的經典教科書例子：(1)英國的某座森林中原本有著黑色和白色的蛾，它們的共同天敵是一些鳥類。(2)19世紀初期工業革命讓英國出現大量的工廠，工廠的廢氣將森林中的樹幹染黑。(3)白色的蛾停在被染黑的樹幹上時，較容易被天敵發現，於是迅速遭到滅絕。

遺傳(Heredity)與變異(Variation)： 生物從胚胎發育成熟的過程被基因編碼(以及一些環境影響)所決定，多數的基因編碼又會透過細胞分裂與生殖過程遺傳給子代。這些生物過程雖然極為規律，但也充滿變異性(例如來自兩性的不同基因，或是基因的突變)。尤其在世代的交替之中，基因層次的變異可能會帶給子代新的型態特徵。而這個變異也將會被“遺傳”給子代。有趣的是，在達爾文的時代中，“基因”的概念尚未成熟。達爾文當年對遺傳與變異另有一套解釋。而這邊使用孟德爾遺傳定律與基因變異的解讀，又被稱為「現代演化綜論(modern synthesis)」或「新達爾文主義(neo-Darwinism)」。達爾文能在不知道DNA的情況之下，將遺傳與變異放入天擇論的核心之中，是不是十分驚人？

競爭(Competition)與適應(Adaptation)： 地球上的能源是有限的，一座小島上的資源是有限的，你家後院花圃中的養分也是有限的，於是不可能讓裡頭的生物無止境地繁殖下去。而在物資不足的情況下就會產生競爭，贏家才有機會將其基因遺傳給後代。這邊提到“競爭”不見得是直接打起來拚死活，有可能純粹是因為不耐乾旱渴死，或是搶食物沒有比別的個體快。於是，適應環境能力較佳的個體比較容易存活下來，並且將自身的基因傳給後代。

演化的證據與證明？

當數學家可以透過邏輯推演從基礎公設中推導出定理，或是物理學家利用極度精準的實驗完美驗證理論預測，生物學家很多時候並無法將抽象的理論百分之百(甚至百分之九十)對應到實際觀察中。也許就像統計學家George Box說的：「所有模型都是錯的，但有些很有用(All models are wrong, but some are useful)」。

因此，當天擇論被提出來時，很不意外並未立刻獲得所有生物學家的認同。反對的人總是可以從一些眉眉角角的細節中挑刺，而支持的人通常也只能先將範圍限縮至非常具體的小例子(例如上圖的黑蛾與白蛾)。經過幾十年正反兩派的論證，從古生物化石到大量的田野觀察、最後加上分子生物學的興起，歷經幾代科學家的交替，天擇論本身也從演化理論的天擇中存活了下來，成為被廣為接受的學說。

接下來，讓我們從以下三個例子中，既看看演化生物學家們如何使用天擇論，也來欣賞一些近代將演化概念擴張的新潮思想。

雌雄二型性

在生物世界中，除了物種之間可以很不同之外，即使是同一個物種的不同性別也可以在外型上差很多！這個現象又被稱為「雌雄二型性(sexual dimorphism)」，在生物界裡的各個分支都十分常見。下圖的三個例子中，你能猜出誰是公誰是母嗎？

(a)鴛鴦，左邊看起來花枝招展的是公鳥。(b)亞歷山大鳥翼蝶，下方是公蝶。(c)密棘角鮟鱇，下方非常小的是公魚。

如何用天擇的角度來理解雌雄二型性的成因呢？「性擇(sexual selection)」背後的機制是什麼？達爾文和Wallace之間曾經有著長達數年對性擇的爭論。其中達爾文認為，主要因素是同性別中的個體為了繁殖機會的競爭，於是長得漂亮的個體有較高的機會將其特質遺傳給後代。而Wallace則傾向是因為在不同物種的競爭中，長得顯眼突出的個體較容易成為被攻擊的目標。於是其中一個性別可能會為了保護另一個性別，而漸漸演化成比較引人注目的模樣。

達爾文和Wallace誰說的比較有道理呢？經過演化生物學家不斷蒐集證據與研究，說實在很難完全給出一個定論，只能說兩人的觀點都或多或少扮演了一些角色，也許在某些特定例子中有辦法試圖論證其中一方的論點稍佔優勢。

從雌雄二型性的例子中，我們看到了天擇論可以用不同的切入點來解釋同一個現象，而且在很多時候很難完全證明一個機制完全勝過另一個解釋。為什麼密棘角鮟鱇的雌性如此巨大而在人類中普遍是雄性比較壯碩？為什麼有些生物是雄性具有鮮豔的外表有些則是雌性？或許我們不該將問題簡化為只能有一個答案？

群擇

在達爾文晚年的著作『人類的由來(The Decent of Man)』中，除了討論了上述的性擇之外，還提及了另外一個極具爭議性的話題：「一群具有強烈道德感的人會比一群暴躁海盜有更多的優勢嗎！？(A tribe a moral men have an immense advantage over a group of fractious bands of pirates!?)」。在同物種間不同群體的競爭與適應，又被稱為「群擇(group selection)」。

另一位近代演化生物學家E. O. Wilson(1929-2021)曾經精闢的描述研究群擇的困難：「在一個群體中，自私的個體會擊敗無私的個體。但是由無私個體組成的群體將會擊敗由自私個體組成的群體。」。天擇的機制是如何在這樣多層次(multilevel)的情況中取得平衡？

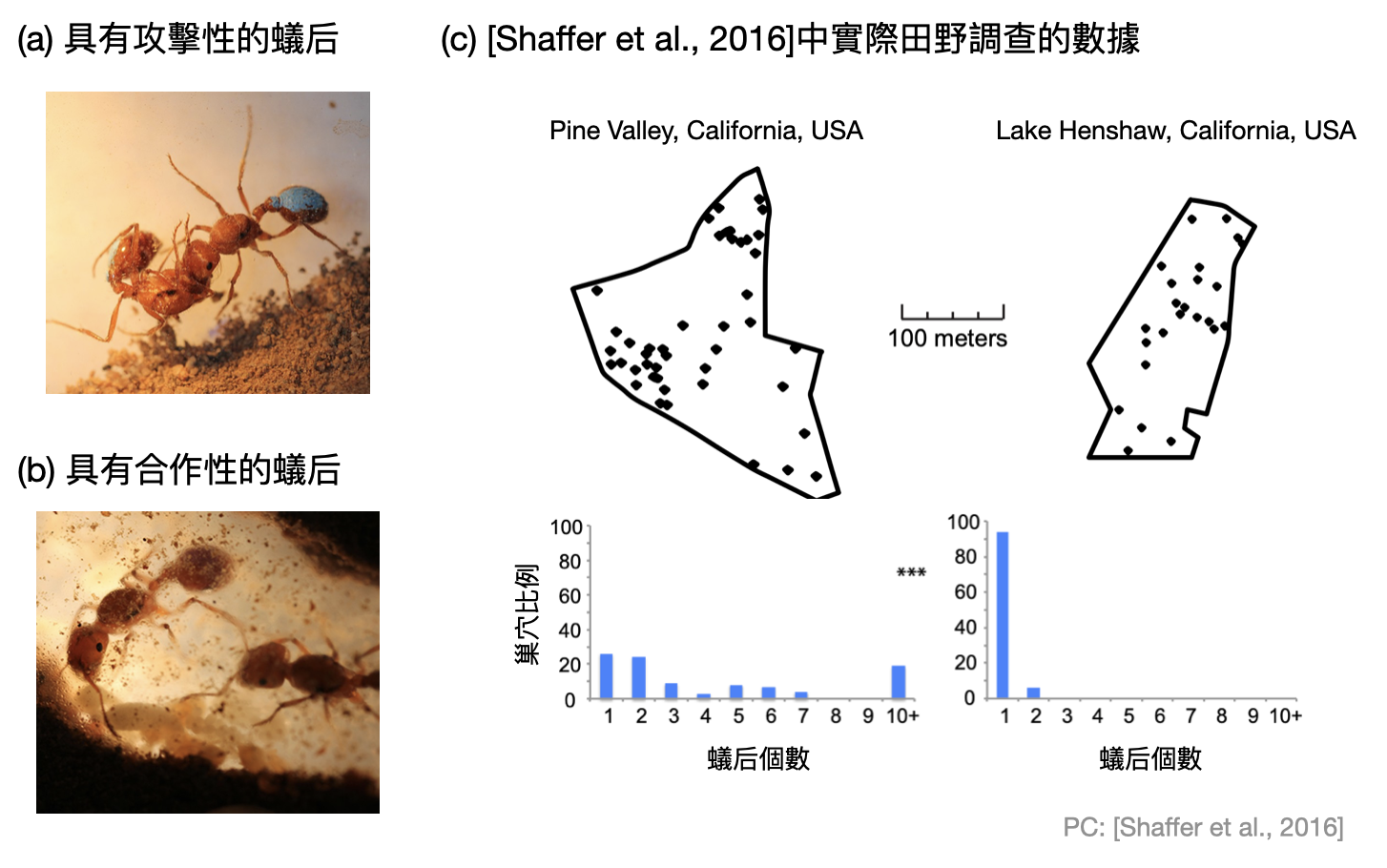
讓我們用一個具體的例子來感受一下群擇中的複雜性：「蟻后困境(foundress’s dilema)」。在螞蟻的巢穴中，通常只會有一隻或幾隻蟻后統領整座巢穴。從田野觀察中可以發現有些蟻后較具攻擊性(如下圖(a))，有些則是喜歡和其他蟻后合作(如下圖(b))。更進一步來說，比較有攻擊性的蟻后相較容易在巢穴中生存。然而，如果一個巢穴中具有多隻蟻后，且其中有的蟻后不喜歡合作，那麼這個巢穴將比較容易滅亡。這些觀察完全呼應了E. O. Wilson對群擇的看法。既然在大自然中可以普遍地觀察到兩種類型的巢穴，到底背後的天擇機制是什麼呢？

在[Shaffer et al., 2016]的研究中，他們考慮了加州須蟻(Pogonomyrmex californicus)的蟻后困境問題。(a)具有攻擊性的蟻后。(b)具有合作性的蟻后。(c)在加州的Pine Valley他們觀察到比較密集的螞蟻巢穴分佈，其中有將近八成的巢穴具有超過一隻的蟻后，而且他們使用的量化工具也顯示蟻后相對比較不具攻擊性。而在加州的Lake Henshaw他們觀察到比較分散的螞蟻巢穴分佈，有九成以上的巢穴都只有一隻蟻后，並且大部分都具有很高的攻擊指數。

在Shaffer與其合作者的研究中[Shaffer et al., 2016]，他們使用單一因子(巢穴的密集程度)來解釋蟻后困境中，群擇在兩個不同層次(巢穴內與巢穴之間)的平衡關係。具體來說，他們提出的理論模型預測出螞蟻巢區比較密集的地方，由於食物競爭激烈，最後會由合作型蟻后的巢穴存活下來。反之，當巢穴相對比較分散時，將會有更多具有攻擊性蟻后的巢穴。而實際在加州兩處蒐集到的田野資料也支持這個理論(如上圖(c))。

群擇以及相關的“親緣選擇(kin selection)”和“利他(altruism)”概念，既吸引人又充滿爭議性。很大的困難點就是如何在有限的田野資料和不完美的數值模型中，剖析複雜的多層次天擇結構。從達爾文與Wallace以降，至今仍是演化生物學界的核心謎團之一。

迷因

不誇張地説，「迷因(Meme)」(如下圖)是許多現代人每天在網路生活中的精神糧食。你可曾想過為什麼迷因叫做“meme”嗎？這個名稱竟然源自於之前提到的演化生物學家Dawkins，在1976年的『自私的基因(The Selfish Gene)』一書！

Dawkins觀察到生活中許多文化元素的傳遞過程，基本上都符合之前提到的天擇論三大核心概念：共同起源、遺傳與變異及競爭與適應。因此，為何不用天擇的概念來理解這些充斥在我們身邊的事物？而由於現在我們知道生物中的特質是透過基因(gene)來傳遞，Dawkins便提議用個類似的名稱“迷因(meme)”來稱呼這些不斷被複製與變異的文化概念。

從這樣抽象的角度來思考，那麼生活中是不是還有許多元素具有類似的天擇概念呢？例如政治中的話語、宗教中的故事、科學中的流派等等，演化的概念將不再侷限於解釋物種的起源，更是提供了一個銳利的視角幫助我們思考事情的變化。

演化與計算

地球從荒蕪演化到現今豐富多樣的世界，這個過程是不是可以看成一個計算的過程？如果是這樣的話，那麼用來解釋演化的天擇論不就可以被看成一個計算原則或是演算法？早在Turing的時代，這樣的想法就已經蠢蠢欲動，並且和人工智慧早期的發展密不可分。在本章剩餘的篇幅中，我們將從「演化演算法(evolutionary computation)」和「演化博弈論(evolutionary game theory)」這兩大領域中一探究竟。

演化演算法

如之前一再強調，自然界中的演化是沒有長期方向性的。然而，一旦我們想要將演化的概念拿來解決計算問題，明確的目標就出現了：要解決這個計算問題！這大概也是為什麼“演化演算法”在中文世界裡有時候又被稱為“進化演算法”，畢竟現在我們有個長期目標了。

如果將演化想成是個最大化適應性(fitness)的過程，那麼是不是可以把天擇的機制拿來設計解決優化問題的演算法呢？這就是演化計算的核心想法。而由於演化和天擇論十分豐富，因此拿來設計演算法解決計算/優化問題時，可以有許多概念元素能夠選用。從最抽象的層面來看，大致上可以把演化計算描繪成下圖中的幾個步驟(如下圖)：(1)將計算問題中的元素對應到基因型與表型，以及設計適應性函數、(2)設置起始族群、(3)選擇能夠繁殖的個體、(4)相互交配產生子代、(5)子代中發生突變、(6)選擇存活下來的子代個體。其中不斷重複步驟2到5直到你覺得滿意或是失去耐心。

先別被這麼多的步驟給嚇到了，在很多應用場景中並不需要將演化計算的所有概念用上，於是根據只使用的少數幾個步驟，或是一些額外加入的概念，便衍生出許多演化計算中的子領域。讀者也許已經可以感受到演化計算具有極大的設計空間讓人把玩，這既是它的優點也是困難點。該如何設計好的基因表示、變異規則、與適應性函數將會非常依靠經驗法則，因此演化計算通常出現在一些實際應用問題的場景，很難有嚴謹的理論分析。

現在就讓我們選幾個演化計算中常見的子領域和應用來見識一下演化概念在計算中的威力吧！

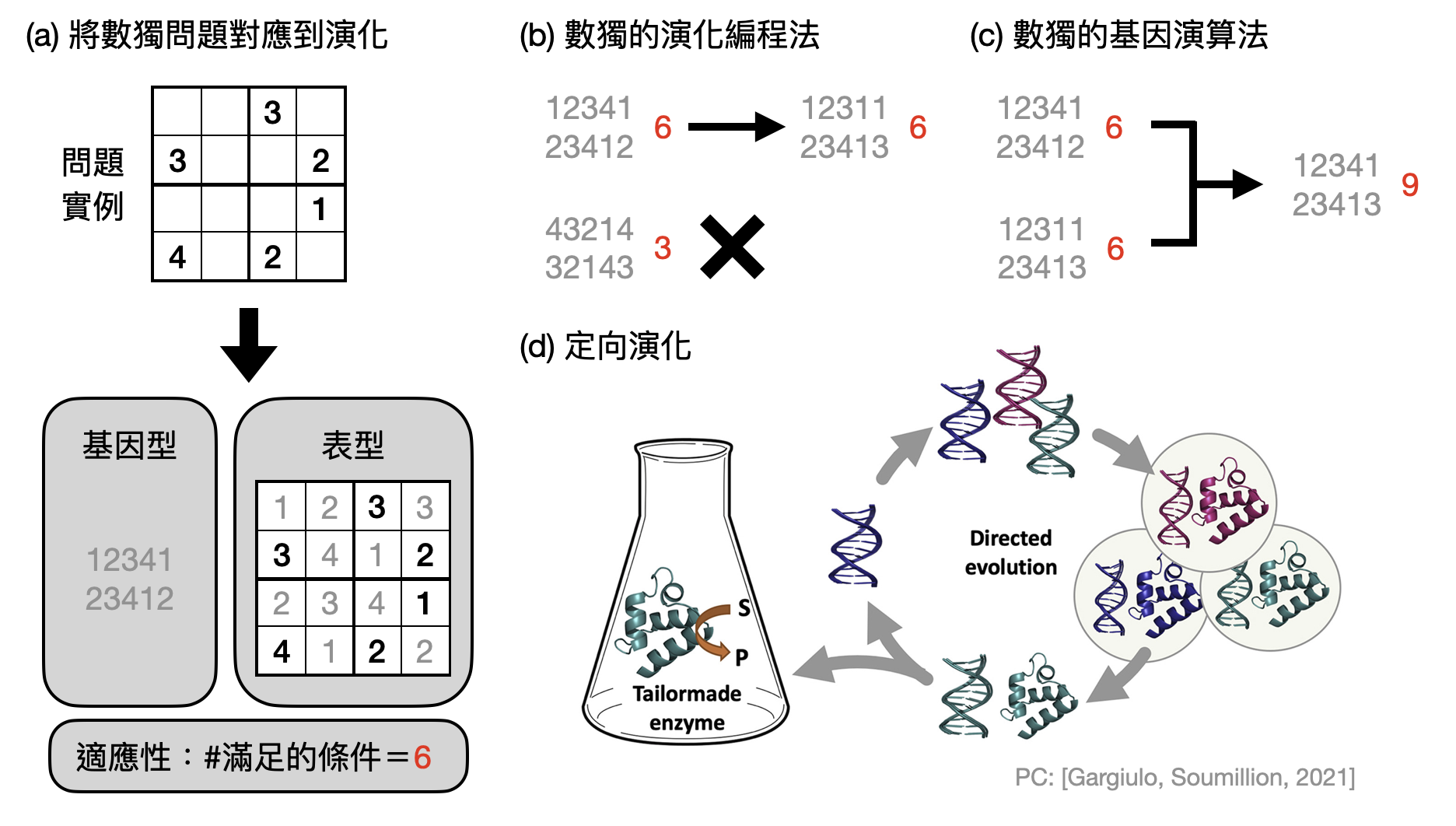
演化編程法(Evolutionary programming) 可以說是最簡單版本的演化計算，也和早期人工智慧的發展互相影響。在演化編程法中，我們將只專注在變異與適應性的設計。具體來說，當拿到一個優化問題之後，只需要設計(1)基因表示與突變規則以及(2)適應性函數，而不需要考慮相互交配的步驟。以數獨問題為例，我們可以直接將每個空格視為一個基因(同時也是表型)，並且隨機初始化其數值。在變異過程中，可以隨機更改(或是不改)空格中的數字。至於適應性函數，則可以根據滿足的行、列和方格數量來做比較(如下圖(a))。

基因演算法(Genetic algorithm) 比演化編程法多考慮了“相互交配產生子代”，期望能夠帶來更強大的計算能力。繼續延伸之前數獨的例子，我們可以在變異的過程之後，隨機選擇兩個解答，並且各取一部份產生出一個新的解答(如下圖(b))。透過設計如何巧妙結合兩個不同的解答，基因演算法時常能表現得比演化編程法還要好。

(a)一個將數獨對應到演化最簡單的方式就是將空白處的數字同時作為基因型和表型，並且定義適應性為滿足的條件個數。(b)演化編程法只會從親代中適應性較高的個體來變異。(c)基因演算法則會多引入親代之間相互交配的過程。(d)定向演化是個用來開發新蛋白質的工具。

定向演化(Directed evolution)： 還記得之前提到的蛋白質結構問題嗎？雖然從DNA序列預測蛋白質形狀非常的困難，不過如果我們心中對於想要蛋白質可以做到的功能有些想法，有沒有辦法回過頭找出相關的DNA序列來產生具有這些功能的蛋白質呢？

Frances Arnold和其團隊利用了「定向演化」的概念成功開發出許多新的酵素(又稱酶, enzyme)，並且因此在2018年獲得了諾貝爾化學獎。利用自然的基因變異，科學家得以獲得大量多樣性很高的蛋白質基因庫，其中有些便可能具有想要的功能。和生物世界中天擇不同的是，定向演化透過了“人擇”來篩選出具有潛力的蛋白質，並且透過分子生物技術大量複製這些有用的基因。如此突變、選汰、放大三個步驟重複多次之後，便可以朝著想要的功能定向演化(如下圖(c))。

演化博弈論

博弈論是個橫跨數學、經濟學、電腦科學、社會科學等學科的理論，因此在這邊將其放在“計算”之下也許會讓一些專家皺眉頭，不過反正本書目前為止已經將計算一詞極度廣義化了，就讓我們別太糾結於領域的分門別類吧！

演化與博弈論之間有著深厚且有趣的關係，為了讓讀者能更品嚐其箇中滋味，在剩餘的篇章中我們將先快速閱覽博弈論的基本概念，然後從兩個演化博弈論的例子感受計算與演化的碰撞。

博弈論(Game theory)與囚徒困境(Prisoner's dilemma)： 最迅速介紹博弈論的方式大概就是透過具體的例子了，而如果只能選一個例子的話那必定得是「囚徒困境」了。

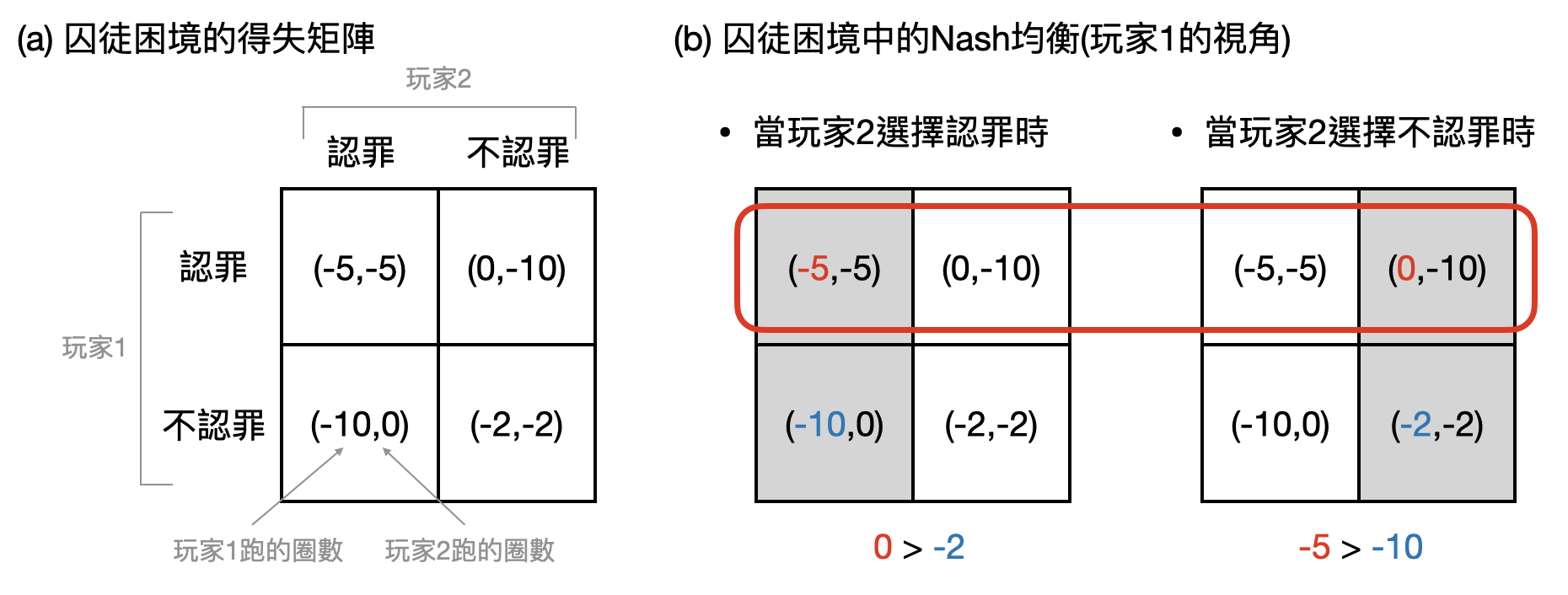
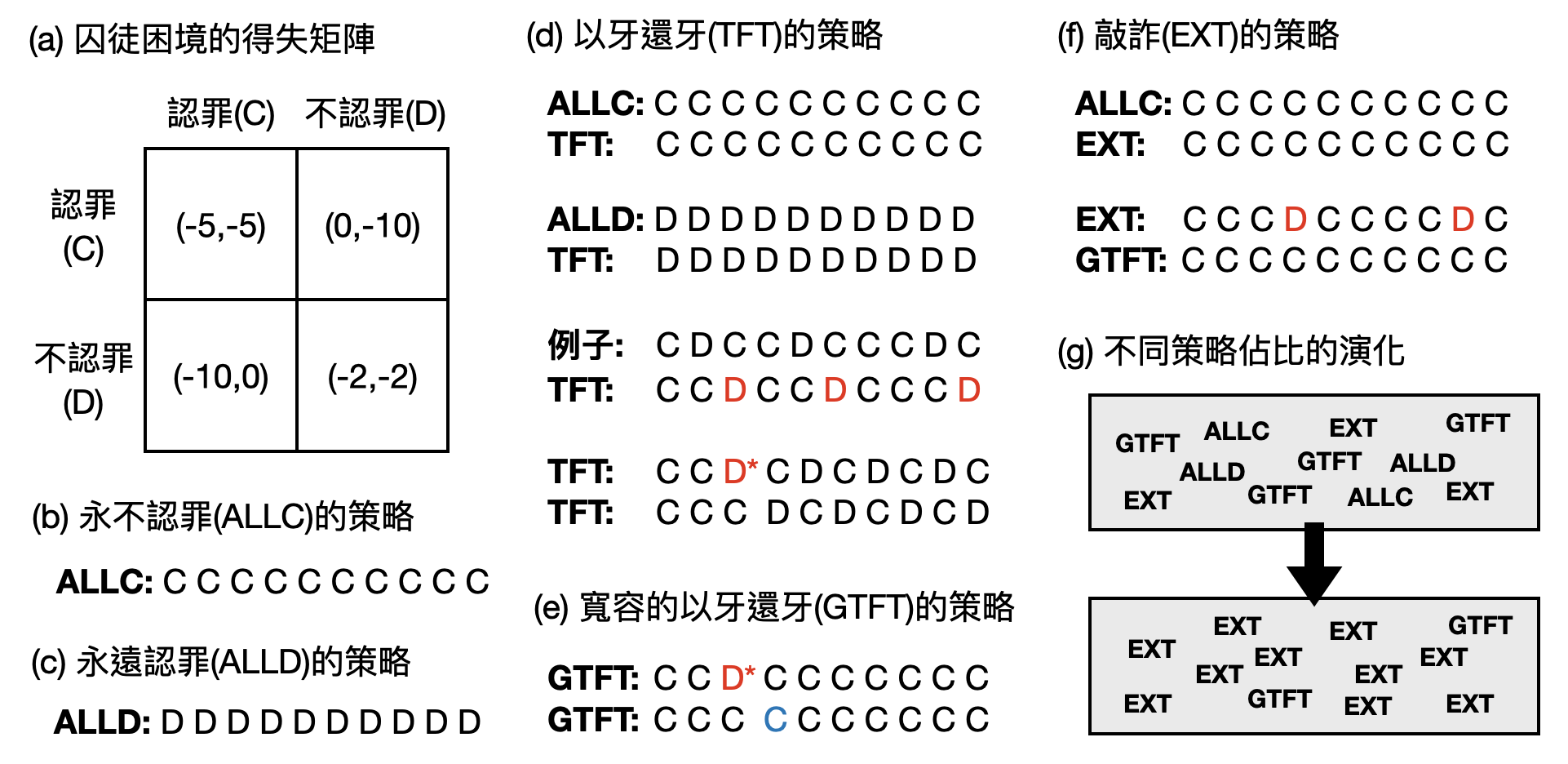
想像你和一個朋友被懷疑聯手在考試中作弊，老師將你們分開審問。根據你們各自是否承認罪行，老師給予的懲罰如下(如下圖(a))：(1)如果兩人都承認作弊，那麼各自罰跑操場5圈。(2)如果兩人都否認作弊，那麼各自罰跑操場2圈。(3)如果一個人承認，一個人否認，那麼老師很會很故意的只懲罰“否認”的人罰跑操場10圈，背叛對方的承認者則不用接受懲罰。在沒辦法和對方溝通的情況之下，你們會怎麼做？

從上帝視角來看，如果你們都否認作弊是個整體跑操場圈數最少的結果(4圈)。然而如果你預期對方會否認的話，就有了誘因去承認而免除罰則。但是如果雙方都是這麼想的話，就會變成兩人都承認，使得整體跑操場圈數大幅提高(10圈)。在沒有一定的信任之下，你們將會不斷揣摩對方的想法，因而陷入“囚徒困境”。

(a)囚徒困境的得失矩陣。根據兩個玩家各自的選擇，將雙方的得失(跑步的圈數)記錄在一個矩陣之中，以方便分析。在一些書中會因為某些博弈的得失矩陣是對稱的(例如本圖中兩個玩家交換角色後，不會影響得失)，所以會將其簡化成只具有括號中第一個數字。(b)當我們說一個玩家的策略是Nash均衡，指的是當另一個玩家改變策略後，原本的玩家的最佳策略(可以獲得最高得失)仍保持原樣。例如在囚犯困境中，玩家1選擇認罪時，不管玩家2是認罪或不認罪，玩家1都不會想要轉換策略，因為紅色的得失比藍色的高。

如此讓兩個玩家有多種選擇，並且任兩選擇的組合都有相對應的“得失(payoff)”數值，就成了博弈論用來描述現實中各種競合場景的數學模型。在數學上，透過John Nash(1928-2015)著名的Nash均衡(Nash equilibrium)，可以更進一步分析理性玩家們會使用什麼樣的策略來做選擇。以囚徒困境為例，其唯一的Nash均衡將會是兩人都承認罪行。

鷹派與鴿派的演化博弈： 兩個物種或是兩種不同生存類型的族群之間的競爭，可以很自然地透過博弈論模型，在設定/假設得失數值之後，分析什麼樣的策略將會達到平衡。不過，在生物的世界中，不像大考是一次定勝負，就算父母代輸掉了一個回合，不久之後子代們就可以捲土重來再論高下一番。也就是說，在描繪物種在演化尺度上的競合時，需要考慮“一串連續的博弈遊戲”！這就是「演化博弈論(evolutionary game theory)」中的核心數學模型。

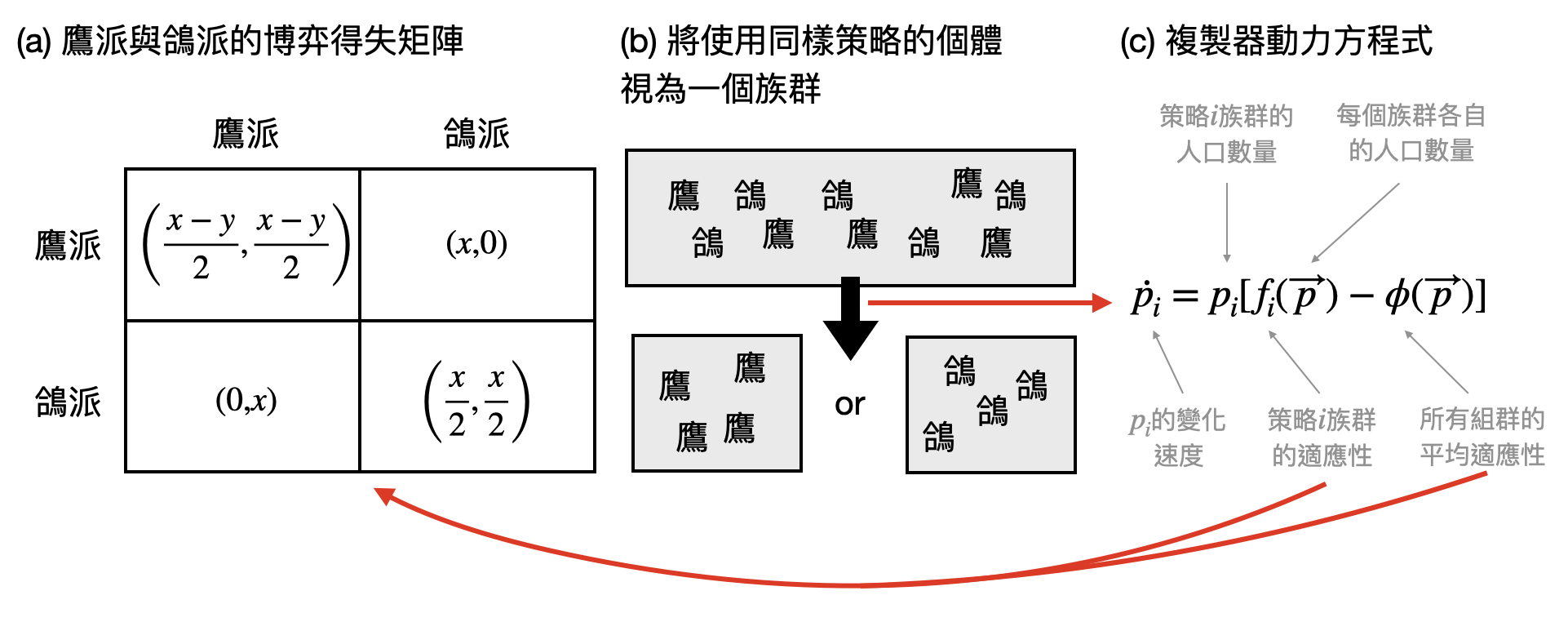
讓我們從比較接近生活的例子來建立直覺。想像你的國家或是你在的公司中有兩種風格的人：鷹派與鴿派。每當鷹派與鷹派的人碰頭時，都會各自堅持維護自身利益，因此在均分資源$x$的同時，會在搶奪中損失了$y$這麼多的價值。因此兩位鷹派人士將各得$(x-y)/2$的得失。而如果是鴿派與鴿派的人碰頭，那麼則會很友善的直接均分資源$x$，各自獲得$x/2$的得失。最後，如果是鷹派角色遇到了鴿派成員，那麼前者將會直接掠奪全部的資源$x$，後者則將一無所有。總結來說，我們可以把這兩種風格人士兩兩遇到時的得失分配，記錄在下圖(a)中的得失矩陣裡。

在工作環境這個大染缸中，職員們來來去去，老職員可能會退休、被裁員或因為不滿待遇而辭職，新進職員也會受帶領他入門的師父影響選擇了相對應的處事風格。在演化博弈論或是更廣泛來說的「演化動力學(evolutionary dynamics)」中，會透過所謂的「複製器動力學方程式(replicator dynamics/equations)」來描述不同類型族群的數量消長。關鍵的是，族群人口數的變化主要和兩個因子相關：(1)當下的族群人口數和(2)族群的適應性程度。而後者則被得失矩陣刻畫。下圖(b)中提供了一個常見的例子。

(a)鷹派與鴿派演化博弈中的博弈矩陣，其中有兩個變數x和y，之後會根據不同的x和y值來分析是否具有不同的演化結果。(b)在演化博弈論中，我們考慮有許多玩家同時在玩一樣的遊戲，並且隨機兩兩遇到。而使用相同選擇策略的個體，將被視為在同一個族群之內。例如在鷹派與鴿派的演化博弈，如果只讓個體固定選擇一個策略，那麼就會有鷹和鴿兩種族群。(c)族群數量的改變由複製器動力方程式描繪，其中族群人口數量的變化率和當下的個體數以及適應性相關。在演化博弈論中，族群的適應性是根據博弈的得失矩陣定義出來的。

那麼，在一個公司或國家中，根據上述的方式演化之下，到底會是鷹派還是鴿派稱霸呢？還是兩種類型的族群間會找到微妙的平衡？John Maynard Smith(1920-2004)身為演化博弈論的創始人之一，發現最終的平衡將會和得失矩陣中的兩個參數$x$與$y$息息相關：當$x\geq y$時，代表鷹派無論如何都可以獲得油水，因此最終整個公司或國家將會演化至所有人都成為鷹派。而當$x<y$時，代表鷹派與鷹派碰頭時將會兩敗俱傷。這時候Smith發現，演化最後的平衡將不會是鷹派或鴿派其中一方完全稱霸，而是最終將會大約有$x/y$比例的人是鷹派，$1-x/y$比例的人是鴿派。這有符合你的直覺嗎？

Smith和他的合作者George Price(1922-1975)沒有就此打住，他們進一步追問：如果有一個族群他們會搖擺在鷹派與鴿派之間，那麼這樣具有“混合策略(mixed strategy)”的族群，有沒有可能稱霸世界？Smith和Price將之前在博弈論段落中提到的Nash均衡，延伸到演化博弈論並定義：「演化平衡策略(ESS, Evolutionarily Stable Strategy)」的概念。他們發現在鷹派與鴿派的演化博弈中，如果有一個族群的策略是在每次交手時有$x$的機率扮演鷹派，$1-x/y$的機率扮演鴿派，那麼這個族群將會具有“演化平衡”。也就是說，如果現在整個公司或國家都是這個族群的人，那麼這個族群就會持續稱霸下去。

無限重複的囚徒困境與合作： 從鷹派與鴿派的演化博弈中，我們建立了演化博弈論的基礎分析架構：透過定義得失矩陣來描述不同選擇所帶來的適應性，接著用複製器動力學方程式來描述族群(可以是固定使用一個選擇，或是用固定的方式交替在不同的選擇中)的數量演化，最後用演化平衡策略的角度分析演化上佔優勢的策略為何。

於是，跟隨上述演化博弈論的分析架構，我們便可以重新思考之前提到的囚徒困境：如果不斷重複進行囚徒困境的博弈(iterated prisoner’s dilemma)，承認罪行會是演化平衡的策略嗎？和單一囚徒困境博弈中，最理性策略是選擇承認罪行很不一樣的地方是，一旦開始重複博弈之後，合作(雙方皆不認罪)將會是個不錯的策略！

然而，演化動力學中許多結果對於最初的數學設定和假設非常敏感，例如在上述的重複囚徒困境博弈中，一旦重複的次數是“有限的”，那麼相互背叛就將會是個演化平衡的策略。如何在數學假設、分析結果和實際世界中的解讀之間取得平衡，仍是前端研究中重要的課題。

(a)囚徒困境的得失矩陣。(b-c)永遠都認罪或永遠都不認罪的策略。(d)除了ALLC和ALLD這兩種固定策略之外，在這邊我們還將考慮使用混合策略的族群，也就是說使用的策略並不見得會固定在一個選擇上。最經典的例子就是以牙還牙(TFT)的策略，也就是完全地模仿對方玩家在上一輪做出的選擇。這個策略乍看之下不錯，但是從圖(d)的第四個例子中，可以看到TFT是個不穩定的策略，一旦稍微有點變化(例如圖中紅色的D*)，就容易造成劇烈的變化。(e)所以學者們也考慮了所謂寬容的以牙還牙(GTFT)策略，使用這個策略的個體會不會立刻報復，而會觀望幾個回合再決定要不要跟隨對方的選擇。(f)有段時間以來專家們都以為GTFT應該就是演化穩定的最佳策略了吧，但是Stewart和Plotkin發現了一個敲詐(EXT)的策略，不但是演化上穩定的，還可以將GTFT族群滅絕。(g)敲詐策略可以稱霸的示意圖，圖中並未根據真實模擬，更多細節請參考延伸閱讀。

總結

在本章中，我們從結構與隨機性出發，沿著歷史之路見識到許多思想家們對物種起源的討論，最終停留在達爾文提出的天擇論。我們看到了天擇論可應用的廣度、深度與彈性，也淺嚐了其和計算以及博弈論之間的聯繫。

在生命世界的研究中，筆者認為最困難的問題就是「why(為什麼)」。為什麼地球上多數的生物有兩種性別？為什麼長頸鹿的脖子這麼長等等。生物學中區分的「近因(proximate cause)」與「遠因(ultimate cause)」便是在嘗試回答why類型問題時，將複雜的因果網路抽絲剝繭的第一步。就像本章開頭引用Richard Dawkins的話：「演化中沒有長遠目標、沒有遠距離目的也沒有終極的完美來作為選擇的基準。」天擇論很聰明地避開正面回答這種why類型的問題，而是反過來用“被篩選”這種被動的角度來理解演化“計算”出來的結果。

近因與遠因之間的糾纏，讓計算在生命世界中所處的位置與其在數學及物理世界中扮演的角色相當不同。雖然增添了不少研究上的難度，但同時也打開了一扇通往豐富多樣的大門。天擇在演化中提供的觀點，或許能夠在未來引導我們對於“無目標計算”的摸索。而與此同時，計算的視角或許也能拓展演化提供的解釋？

延伸閱讀

教科書與其他教材：

內文引用的論文：