第10章
最後的謎團:腦神經科學
There is no scientific study more vital to man than the study of his own brain. Our entire view of the universe depends on it.
沒有任何一個科學研究可以比研究我們自己的大腦還要令人興奮了,我們所有對於世界的認識都是建構在其之上。
Francis Crick
當數學家斬釘截鐵地否決了萬能計算機的存在,當物理學家信心滿滿地告訴人們宇宙遠處有無數深不見底的黑洞,當演化生物學家用天擇論解釋了物種的湧現並且嘗試理解人性,我們卻對於自身大腦的運作方式一知半解。近年來隨著實驗及分析技術越來越成熟,高效能的電腦、機器學習的輔助與數據分析的理論等源自電腦科學的工具,成了腦神經科學家的新寵。同時,更多的資料和數據也帶來了更多的疑問與好奇。計算的思維,是否有機會帶給腦神經科學新的理論視角?
腦神經科學的春秋戰國時代
中國歷史上的春秋戰國時代中,不只群雄割據四方,在思想上更是百家齊鳴。而腦神經科學現今的發展盛況,可說是毫不遜色於當年的秦齊楚燕與儒墨道法。既有大量醫療相關的研究從腦神經疾病出發,也有理論物理的研究建立數學模型探究大腦的方程式。幾年前果蠅的全腦連結圖(有三千多腦神經細胞、五十多萬個細胞連結)才被建成,同時最新一代的電生理學探針已經可以側錄數百個神經細胞的活動。在這樣極度跨領域又多元的課題上,缺點是每個人都會有很多不知道的東西,但硬幣的反面,同時意味著存在空間讓不同的方法論大顯身手
在本章中,我們將先迅速地走訪幾個腦神經科學的子領域,建立一些基礎知識與共同語言。接著,我們將從計算的視角來看看九個在過去半世紀以來腦神經科學中振奮人心的發展。
細胞與分子腦神經科學
成年人的腦中大約有一千億個腦神經元(neuron, 或稱腦神經細胞,在之後簡稱為神經元),另外還有2到10倍的神經膠質細胞(glial cell)扮演輔助的角色。不過由於神經元是主要傳遞神經訊號的角色,所以大部分的研究都是著重在其之上。以下我們將從幾個不同的角度,簡單介紹神經元在細胞與分子層次中的基礎運作。
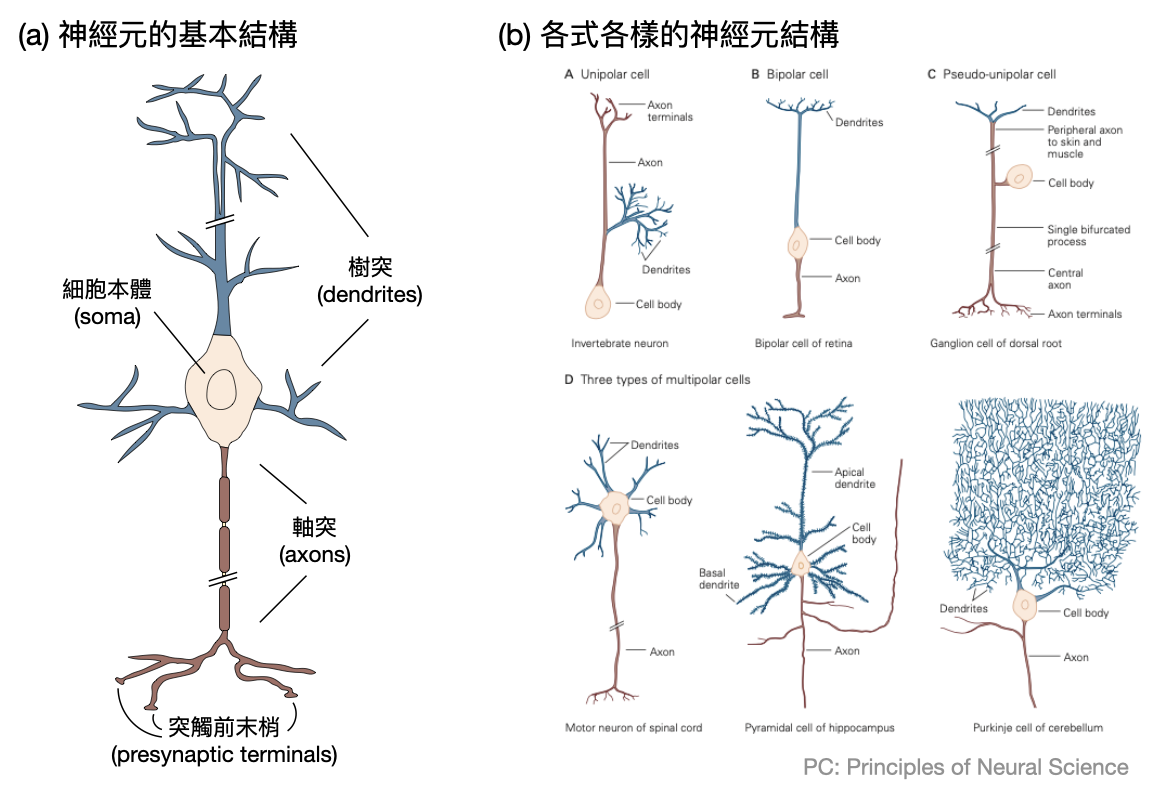
神經元的基礎結構: 神經元的種類有千百種,在不同層級的動物中也會稍有不同。從最抽象的角度來看,一個腦神經元主要有四個區域:(i)細胞主體(soma)、(ii)樹突(dendrites)、(iii)軸突(axon)與(iv)突觸前末梢(presynaptic terminals)。
顧名思義,細胞主體負責維持細胞的代謝與運作,並且儲存基因資訊。樹突和軸突會從細胞主體延伸出去,分別扮演接受訊號和傳送訊號的角色。剛接觸腦神經科學時很容易將這兩者的角色搞混,一個簡單的記憶方式如下:在等候訊息時,由於不知道訊息會從何方而來,所以會盡量廣設接收用的設施,因此使用“樹狀”的結構來最大化接收的範圍。至於傳送訊息時通常目標很明確,所以只要單一“軸狀”的發送結構就可以乾淨俐落的抵達訊息傳送地。最後,軸突的末端會稍微分散成數個突觸前末梢,來和各個接受訊號的神經元接觸。
當然,上述的四大結構及相關的基本結構和功能都只是概述而已,真實的神經元具有極為多元的種類和令人意想不到的樣貌與行為。至今在研究的前線仍有無數的細胞與分子腦神經科學家努力地建立不同神經元種類(cell type)的圖鑑。
說了這麼多,到底神經元是如何傳遞和表示訊號呢?自從Alan Hodgkin(1914-1998)和Andrew Huxley(1917-2012)在1939年首次從章魚巨大的神經細胞中側錄到電訊號,目前主流的看法認為電訊號是大腦傳遞訊息的基礎單位。然而不像在電腦中是使用高電位與低電位來表示0與1,在腦神經的世界中,電訊號所表達的訊息為何仍是個大謎題。對於某些被研究多年的腦區或動物,專家們也許對其中電訊號的意義有一些共識,不過在大部分的情況中我們仍處在一個瞎子摸象的階段。
雖然目前人們還無法完全理解電訊號背後的意義(或是背後根本沒有意義?),不過透過大量的實驗,人們至少對於腦中電訊號的運作機制有非常清晰的認識。以下,讓我們迅速地一覽這些概念。首次接觸相關知識的讀者,可以著重在大方向上的規則以及建立對相關名詞的印象,這樣在未來見面就不會怕生了。
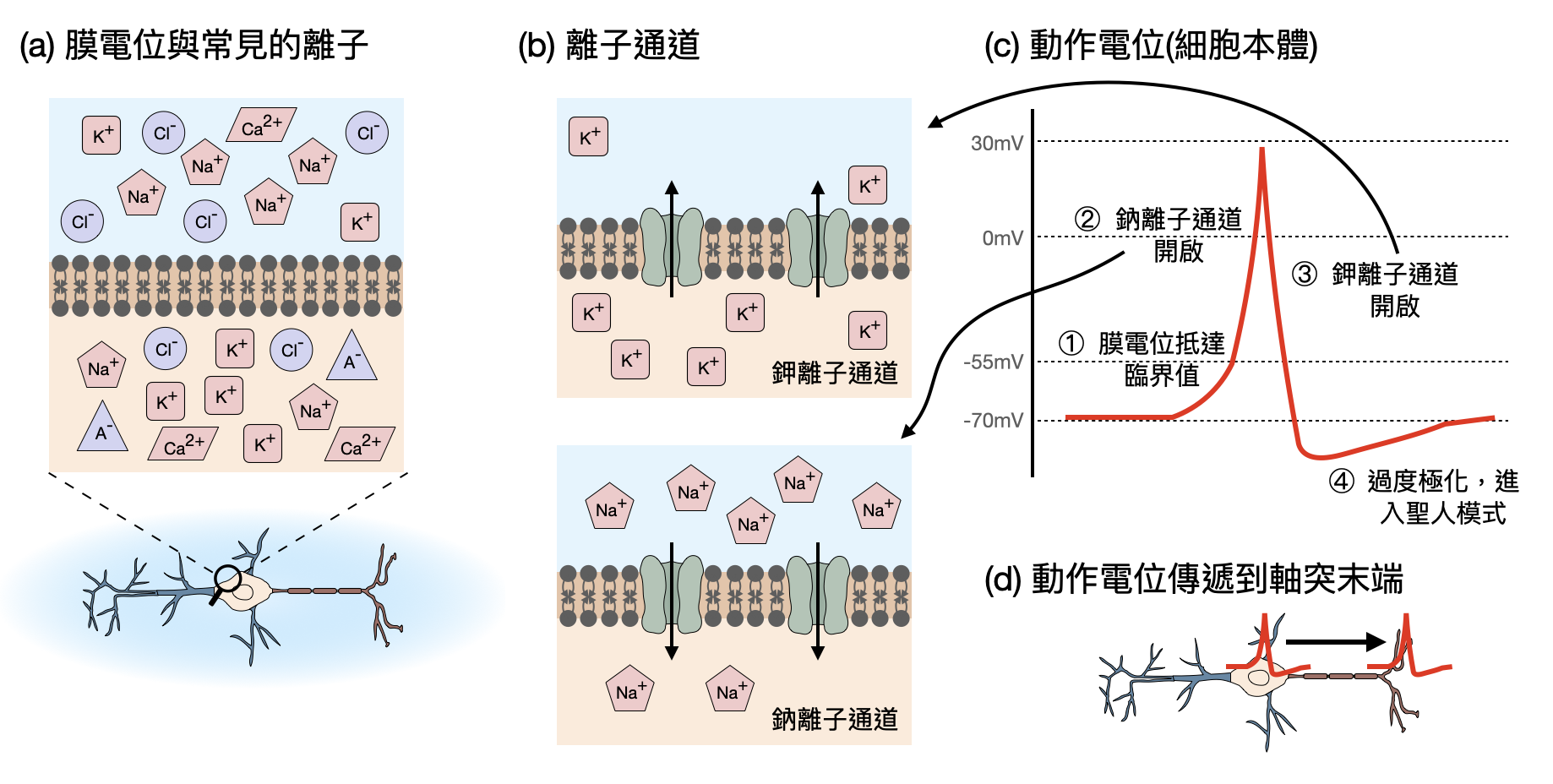
單一神經元的運作-膜電位、離子通道與動作電位: 神經元的細胞膜將細胞內外的世界一分為二,即使是很小的電離子們都無法任意通過。因此,四種常見的電離子:鈉離子(sodium, Na+)、鉀離子(potassium, K+)、氯離子(chloride, Cl-)和鈣離子(calcium, Ca2+),依據相對濃度的比例,將造成神經元細胞內與外的電位差(在細胞主體處),這又被稱為「膜電位(membrane potential)」(如下圖(a))。
細胞膜也不是這麼無情的,許多由複雜蛋白質組成的離子通道(Ion channel)會根據個別離子的濃度差距或是特殊訊號來決定是否導入或輸出某種離子(如下圖(b))。這些離子通道扮演著重要的調控角色,讓神經元能夠敏感地掌控非常細微的電位變化,並且細緻地變化其膜電位。
在離子通道的調控之下,神經元的膜電位通常會處在一個「休息電位(resting potential)」上,大約在-70mV左右,是透過特殊通道(例如鈉鉀離子幫浦(Na+ K+ pump))用能量(ATP)來維持離子濃度差造成的。如果其他神經元在短時間內傳遞了許多訊號,造成膜電位升高至-55mV,那麼就會引起「動作電位(action potential)」,在短時間內拉高(depolarization)緊接著降低(polarization)神經元的膜電位,並進入一個暫時的聖人模式(refractory period)(如下圖(c))。動作電位的一番大動作,會連帶讓軸突也產生電位波動,因此將這個“訊息”(發生了一個動作電位)由細胞主體迅速傳播到軸突末端,準備發送給其他神經元(如下圖(d))。據外型上的特徵,動作電位常被稱為「電脈衝(spikes)」。
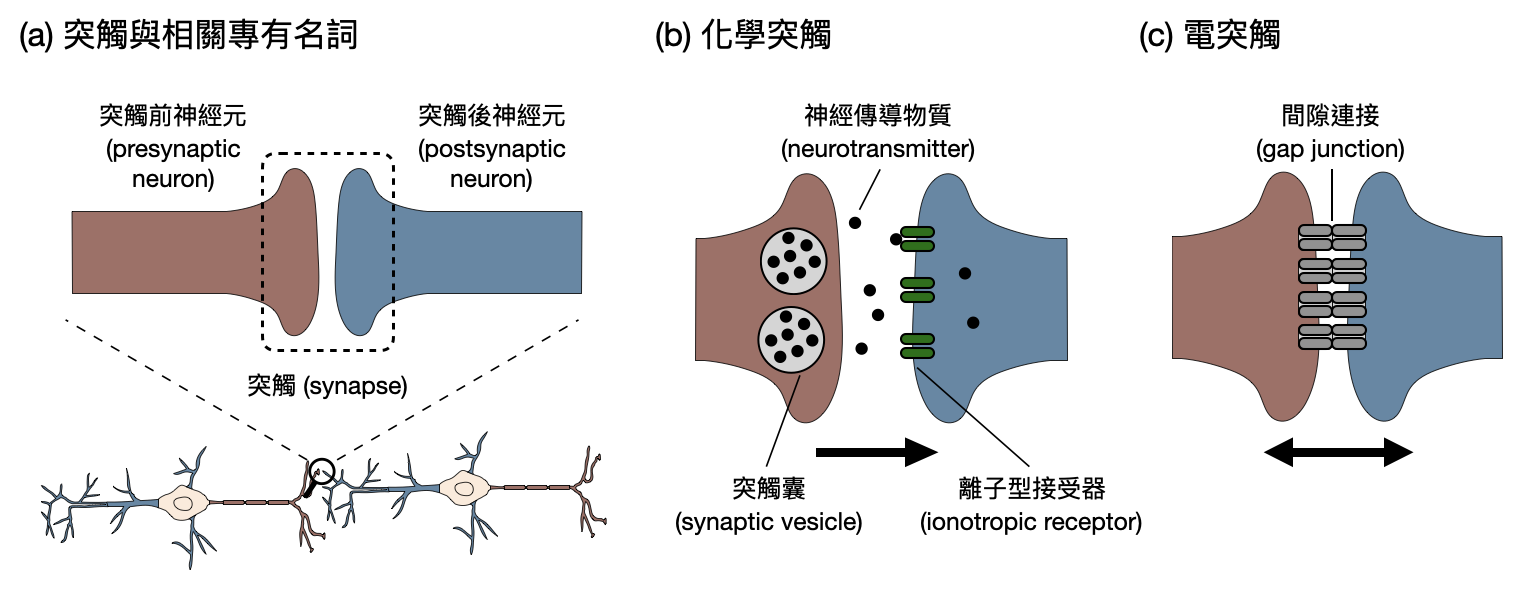
神經元之間如何交談-突觸與突觸可塑性: 神經元的樹突和軸突就像是它的手一樣,只不過兩個神經元在牽手時只能其中一個使用樹突另一個使用軸突,而牽手的地方又被稱作為「突觸(synapse)」(如下圖(a))。當突觸前的那個神經元(也就是使用軸突的那個)產生動作電位,並將訊號如前所述帶到突觸前末梢時,根據突觸的類別(化學突觸或是電突觸,如下圖(b)和(c))會用不同的方式改變突觸後神經元的電位。
如同當比較熟之後握手可能會比較大力一樣,突觸造成電位改變的大小也是可能會隨著兩個神經元的互動頻繁程度等等而改變,這樣的性質又被稱為突觸可塑性(synaptic plasticity, 如下圖(b))。這個特質是許多腦神經科學家認為腦子在學習時使用的重要機制。
系統腦神經科學
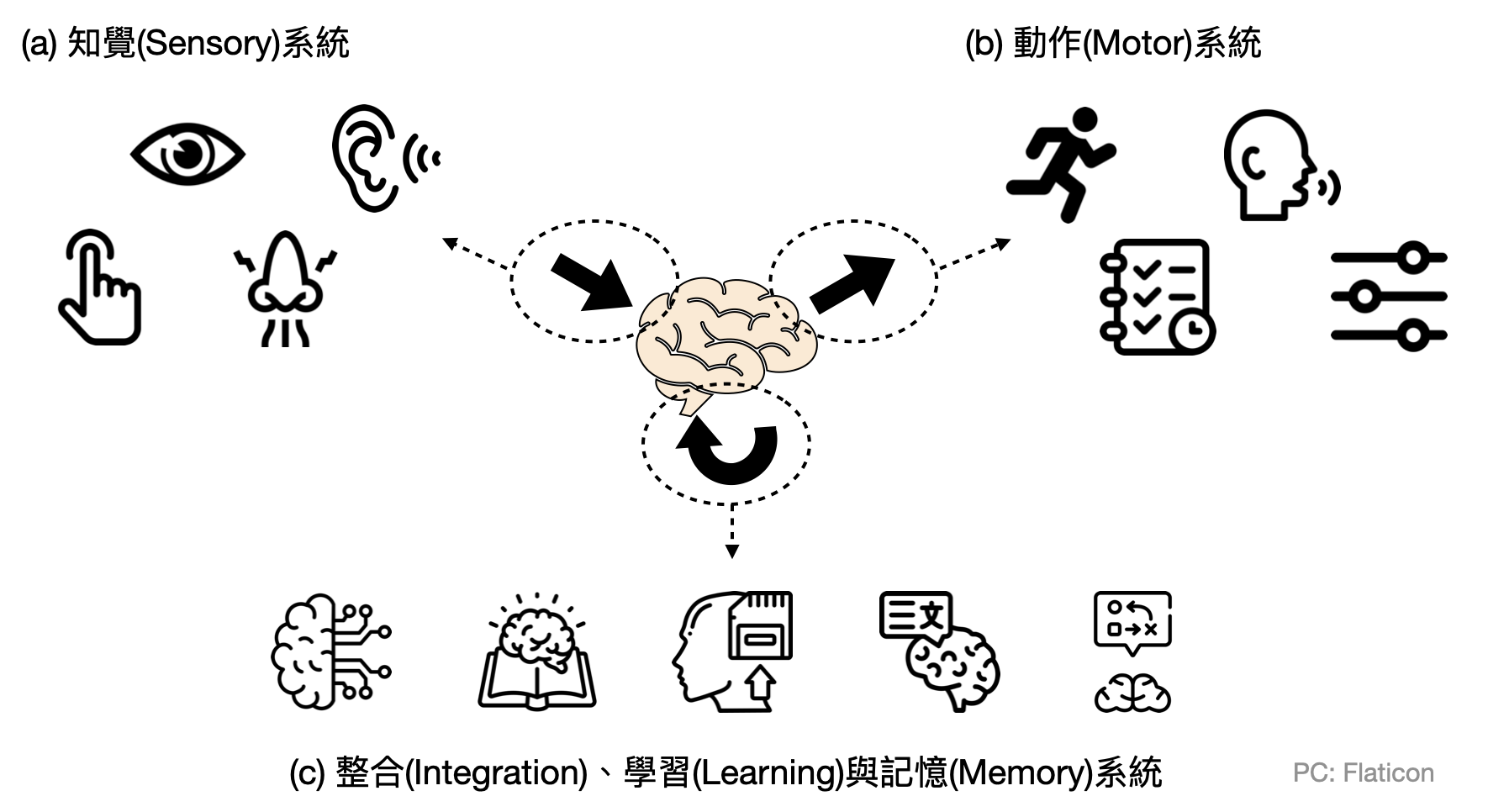
大腦的構造並非雜亂無章,而是具有不同的層次。就像是政府的各個院會(以台灣為例,行政院、立法院、司法院等等)各司其職,腦中的各個區域會負責不太一樣的“功能”,因此根據功能及解剖學上的相似/相鄰性,便會被科學家歸類成為一個系統。
系統腦神經科學(System neuroscience)就是在研究腦中各個結構和系統所對應的功能,以及和知覺與行為表現的關聯。當然,生物世界不像人造世界一樣可以有明確的分工,腦中的各個小系統不見得會完全只負責一項工作,甚至系統之間的區分邊界也沒有那麼乾淨絕對。所以在學習時千萬要抱持著開放的態度,而非一昧將目前系統腦神經科學提出的理論當成真理。
就像在社會課本中介紹政府結構時,會先概述一府五院,以下將介紹一種將腦中系統分類的方式(每個腦神經科學家可能會有各自分類的喜好,這邊的分類是根據筆者的理解),讓讀者淺嚐系統腦神經科學的風味。
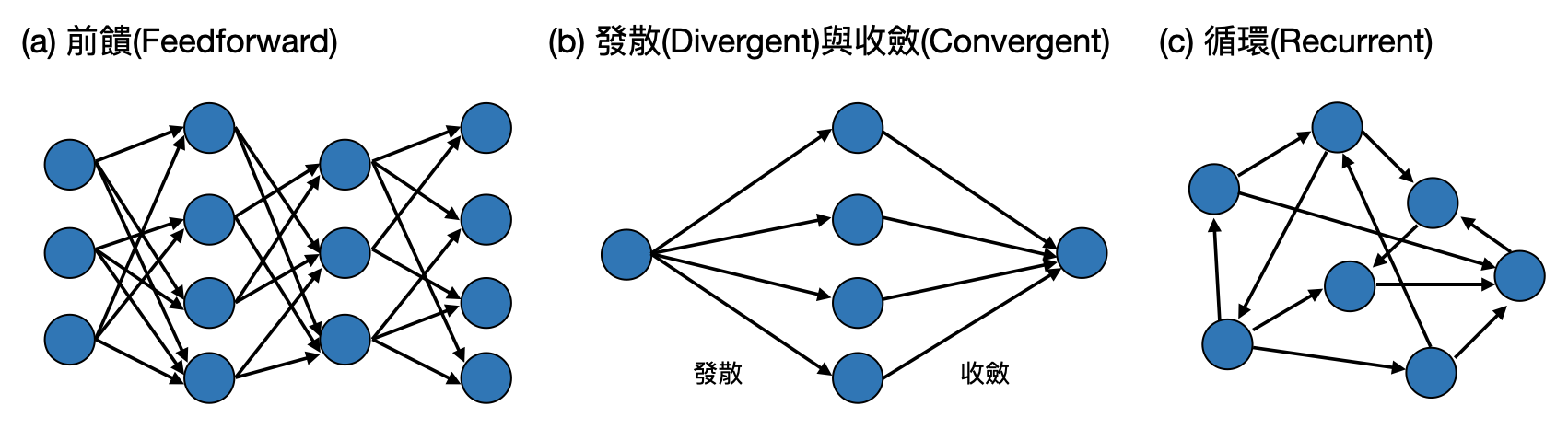
腦中的部門-線路(circuits)與線路模體(circuit motifs): 上述幾種類型的大系統,就像是政府的各個院會,在每個院會中都還會有許多部門。這些部門除了和內部自己人互動之外,也會有不少跨部門甚至跨院會的交流。在大腦中的“部門”通常會是由一群型態與行為類似的神經元相連而成,這樣數十至數百數千個神經元組成的部門,在腦神經科學中通常被稱作為一個「線路(circuit)」。如同在政府單位中的部會有一些常見的組織架構,腦中的線路也有一些常見的「模體(motifs)」,以下就讓我們來看看四個常見的模體。
大方向的簡介可能還沒辦法讓讀者感受到系統腦神經科學最前沿的風景,以下讓我們來欣賞一個近年果蠅腦中導航系統的最新研究。
果蠅的導航線路: 每到夏天溫度高到一定程度的時候,果蠅們就會悄悄地從廚房陰暗潮濕的垃圾桶或排水道大量湧現,相信是許多廚藝愛好者的夢魘。而果蠅在生物學上的屬名Drosophila正恰恰反映了它們的習性:"Droso"是拉丁文中的“潮濕”,"phila"則對應到了“喜愛”。下一次在論文中看到Drosophila時,別再以為是什麼希臘女神的名字了!
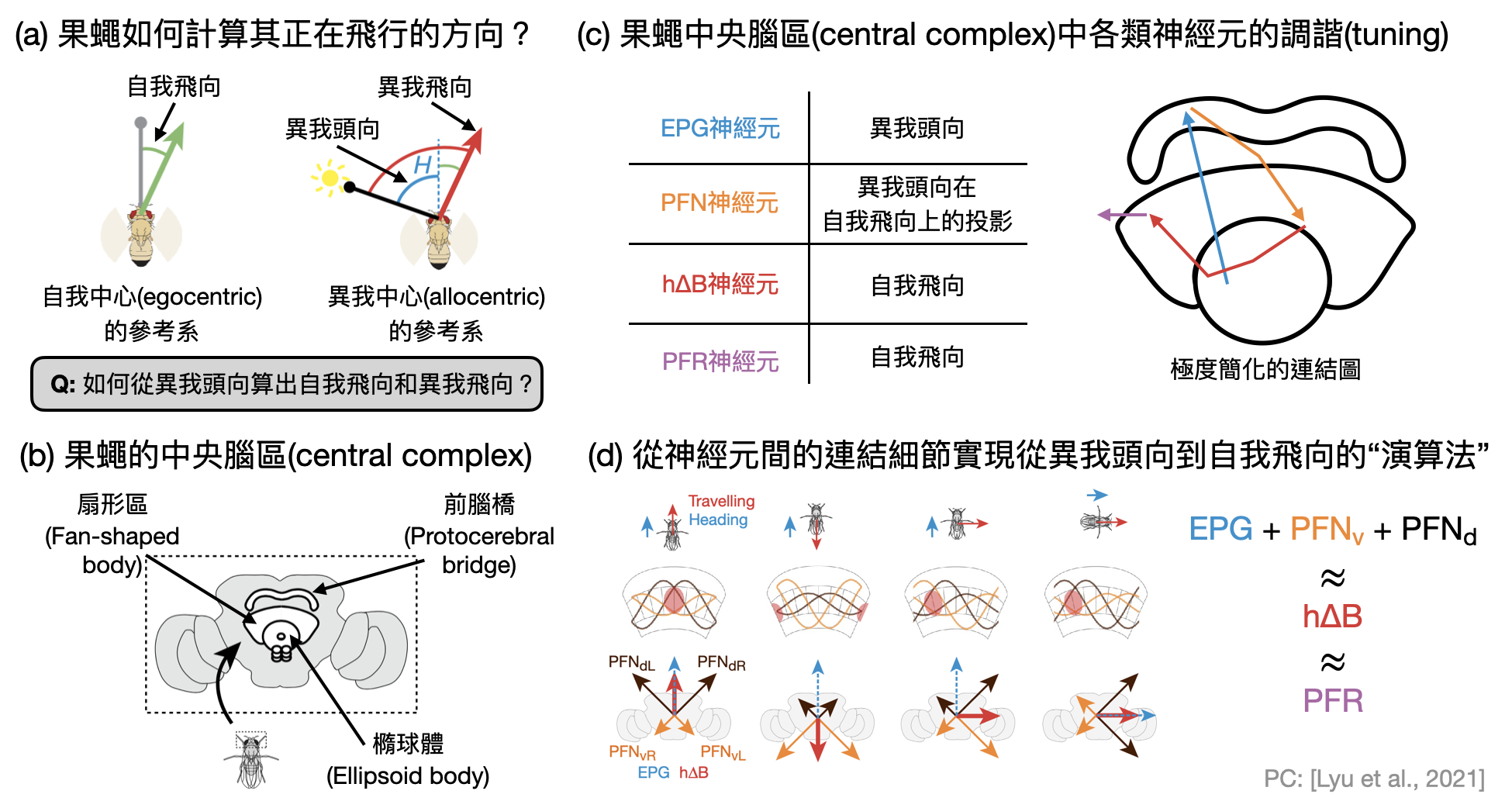
想像一下你是隻果蠅,在一間忘記打掃的廚房中開心地尋覓食物,食物的氣味從四面八方而來,你的頭也不停地四處張望,空氣中的些微擾動可能也會干擾你的飛行,你的大腦會如何幫你校正這一些不確定因素,幫助你飛往食物的方向呢?
關於“果蠅導航系統”的問題,是非常經典的系統腦神經科學研究方向。在下圖中,我們將看到Lyu、Abbott和Maimon用一個向量演算法,來理解果蠅不同腦區的幾種神經元如何組成線路並從對外界的定位計算出其實際的飛行方向。
計算腦神經科學
隨著電腦計算能力的提升與普及,人們開始可以透過電腦來模擬複雜的系統,而這之中當然也包含了大腦。雖然離完全模擬大腦所有行為還很遙遠,然而對於單一神經元或是數十數百個神經元組成的小系統/線路,一旦能夠將基礎的交互作用關係以及化學反應細節描述清楚,透過電腦模擬便能獲得很不錯的近似結果。同時,電腦及資料處理科學也提供了分析處理實驗數據的平台和方法。因此,在這個多元的時代背景之下,計算腦神經科學(Computational neuroscience)就應運而生了。
身為一個新興領域,每個人對計算腦神經科學可能都有些略微不同的定義,或是說,這個領域仍然在成長與演化。一旦用到了計算的模型,或是使用了計算的分析方法,那就有很高機會被貼上計算腦神經科學的標籤。以下將用近年來火紅的人工神經網路作為例子,在之後的內容中,我們將會看到更多。
人工神經網路(Artificial neural networks): 人工神經網路泛指模仿、或是從生物大腦結構獲得靈感的人工計算模型(在第三章中曾經簡單介紹過)。近年來透過不斷地加深和加大人工神經網路,在工程上已經取得以前完全想不到的成功(例如圍棋、蛋白質結構、影像辨識、語言模型等等)。這樣令人興奮的進展,是否能夠反過來推進我們對自身大腦的理解呢?
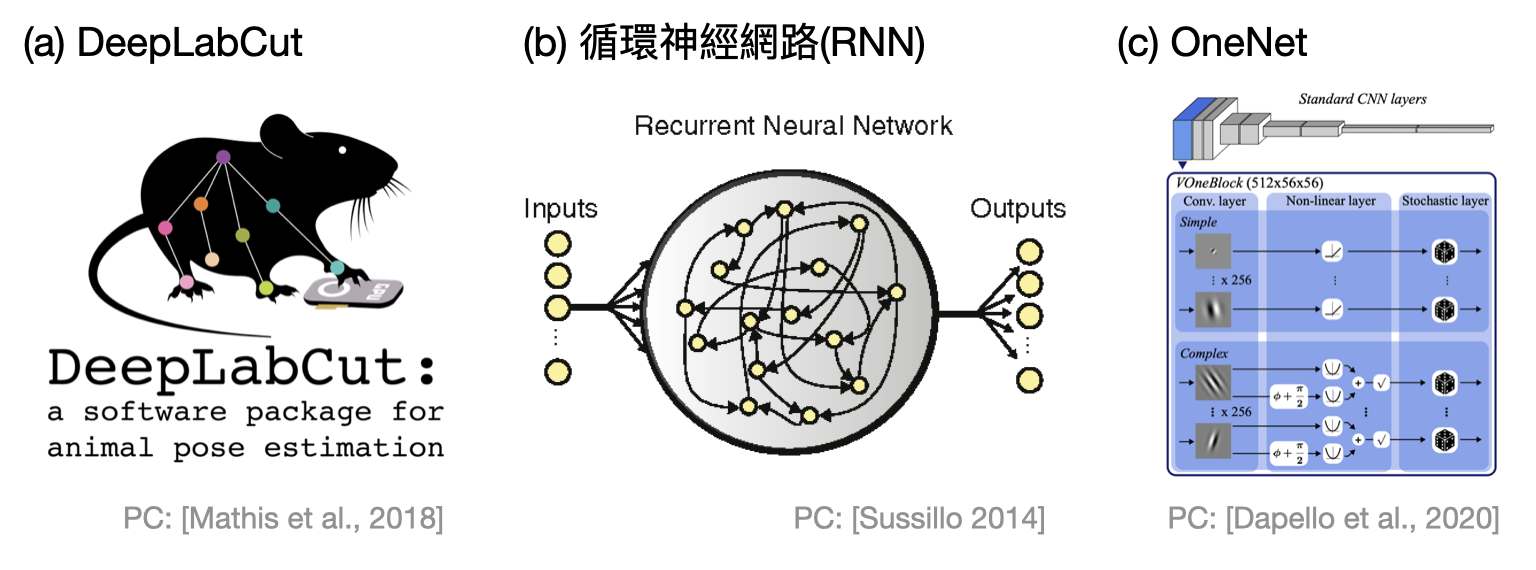
除了最直接的使用人工神經網路來協助分析資料之外(如下圖(a)),有些學者開始使用一些人工神經網路(尤其是循環神經網路(recurrent neural network, RNN))作為某些系統的模型,以便進行量化的分析(如下圖(b))。另外一個常見的流派則是使用人工神經網路來學習真實腦神經數據的輸入輸出訊號,進而在學習後的結果模型上做分析(如下圖(c))。
總結來說,將人工神經網路的進展應用在腦神經科學的研究,目前仍處於前奏曲的階段,未來的發展令人非常期待。
認知腦神經科學
顧名思義,認知科學是門研究“認知(cognition)”的學科。由於“認知”一詞具有太多的涵義與解讀,所以認知科學處於各大學科(例如語言學、心理學等)的交集。傳統認知科學主要採取的是相較“由上而下(top-down)”的研究方法論,研究人員通常專注在行為(behavioral)層面,並試著找出大方向的原則,對於生物的實作細節就相對沒那麼重視。而認知腦神經科學(cognitive neuroscience)則試圖在有腦神經底層實作或腦神經活動實驗數據的背書之下,研究諸如意識、記憶、語言和情緒等主題。
隨著時代的演進,人工智慧的蓬勃發展以及腦神經科學實驗技術的突飛猛進,讓這些不同的領域有了相互刺激影響的契機。說不定在我們有生之年,有機會看到神經元連結互動的細節,是如何湧現出高層次的認知與智慧?
常見的腦區簡介
假如有個外國人想要請你介紹你的家鄉,你會怎麼做?你的第一反應也許是先從你最愛的小吃攤講起,但說著說著你馬上發現對方對於那些小吃的類型從沒看過,所以你只好抽象地先描述一下主要的食物類型。接著你可能介紹了幾個你週末常去玩的地方,像是去淡水河畔跑步打球、到中山區吃拉麵、到華山文創園區逛展覽等等,結果對方突然問,怎麼沒有提到故宮博物館呢?上述的窘境也會發生在要介紹大腦結構的時候,不管用什麼順序/方式介紹都一定會有些遺珠之憾或不通順之處。於是就像在前言提到的一般,與其想成是條列式的學習一堆規則,倒不如想成是在蒐集拼圖的碎片,總有一天這份拼圖的洞會越來越少。
打了這麼多預防針,希望以下的簡介能讓初次接觸腦神經科學的讀者能夠建立起簡單的藍圖。
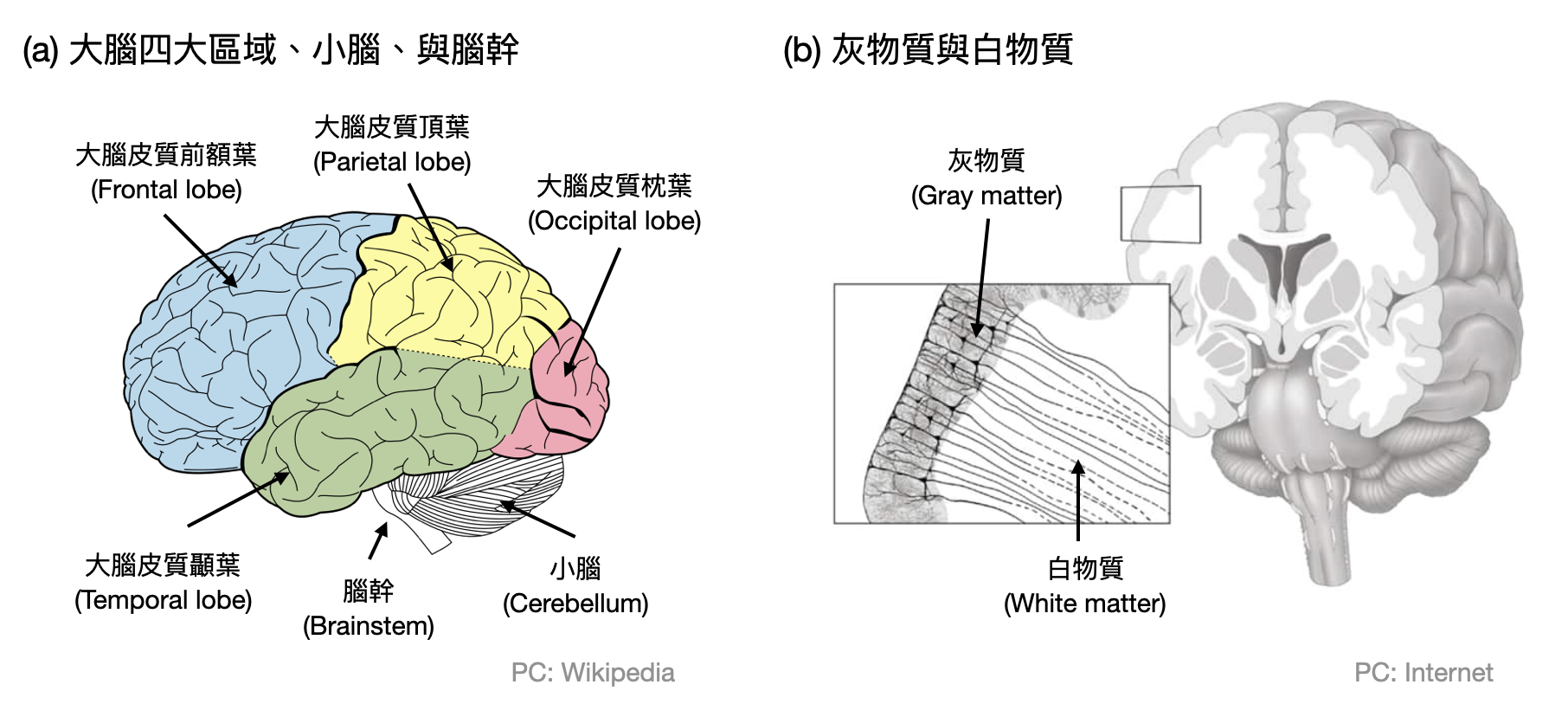
整體概述: 成年人的腦約重1.2到1.5公斤,佔人體總重的2%左右,然而其能量(氧氣和卡路里)消耗是全身的20%。在結構上大致可以分為三區:大腦(cerebrum)、小腦(cerebellum)與腦幹(brainstem),如果講究一點可以依據所處位置的前/中/後及腹側(lateral)/背側(dorsal)進行細分。
在大結構上,腦由俗稱的灰物質(gray matter)包覆著內部的白物質(white matter)。灰物質主要由神經元的細胞本體(soma)組成,白物質則是大部分包含著突觸(axon),我們可以由此看到神經元是很井然有序的排列在腦中。
大腦(Cerebrum)可以說是人腦中最重要的區域,以至於在中文世界人們常常用“大腦”一詞來意指整顆腦。大腦負責了各種知覺感官、動作行為、語言、決策、情緒、學習等等。這些功能並不是完全混在一起由大腦運作的,而是能夠透過實驗很明確地發現由大腦中不同的子組織各司其職(當然還是無法排除可能有些整體的運作機制)。以下將介紹四個大腦中時常被研究的區域。
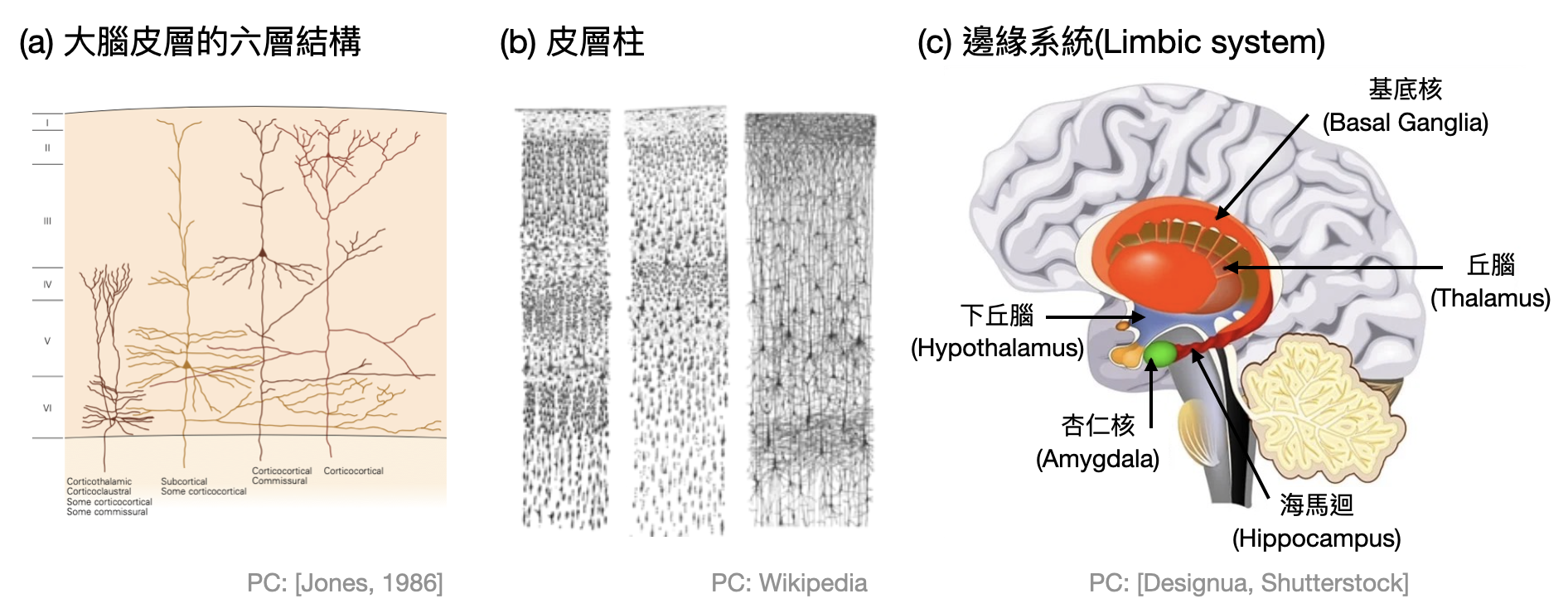
- 大腦皮質(Cortex)指的是大腦外層的灰物質,以皺褶的方式出現因而擁有巨大的表面積,並且大約佔整個人腦重量的一半。在組織上大腦皮質具有對稱的兩個半球,左半球控制右半身,右半球控制左半身。在大腦皮質中通常具有明顯的六層結構(下圖(a))。並包含上億個皮質柱(cortical column)。每個皮質柱大約有一萬個神經元橫跨大腦皮質的六層,並且有大量的內部連結(下圖(b))。根據實驗中發現的功能和所處的位置,大腦皮質又可以被進一步分為四個額葉:前額葉(Frontal lobe)、頂葉(Parietal lobe)、枕葉(Occipital lobe)和顳葉(Temporal lobe)。
- 丘腦(Thalamus)位於大腦中間,連接感知與動作訊號到大腦皮質的各區,並且接受大腦皮質傳回來的反饋訊號進行整理。丘腦的內部結構由約60個各自對應特殊功能的腦核組成,例如LGN(Lateral Geniculate Nucleus)負責連結眼睛與大腦皮層中的視覺區域,其中也和大腦皮質一樣具有六層結構。
- 基底核(Basal Ganglia)位在大腦深處,和大腦皮質、丘腦、腦幹等腦區都有大量的連結。在功能上基底核主要處理動作的控制與協調、行為的選擇、以及學習等等。基底核中主要接受外界輸入的區域是紋狀體(Striatum),可怕的帕金森氏症(Parkinson’s disease)的主要成因就是紋狀體缺少了多巴胺(Dopamine)神經支配。
- 海馬迴(Hippocampus)位於顳葉中,因為其形似海馬而得名。在功能上被認為和記憶與導航相關。在1971年John O’Keefe和Jonathan Dostrovsky發現位於此處的「位置細胞(place cell)」,而促使海馬迴成為研究的熱點(O’Keefe也因此在2014年獲得諾貝爾生醫獎)。
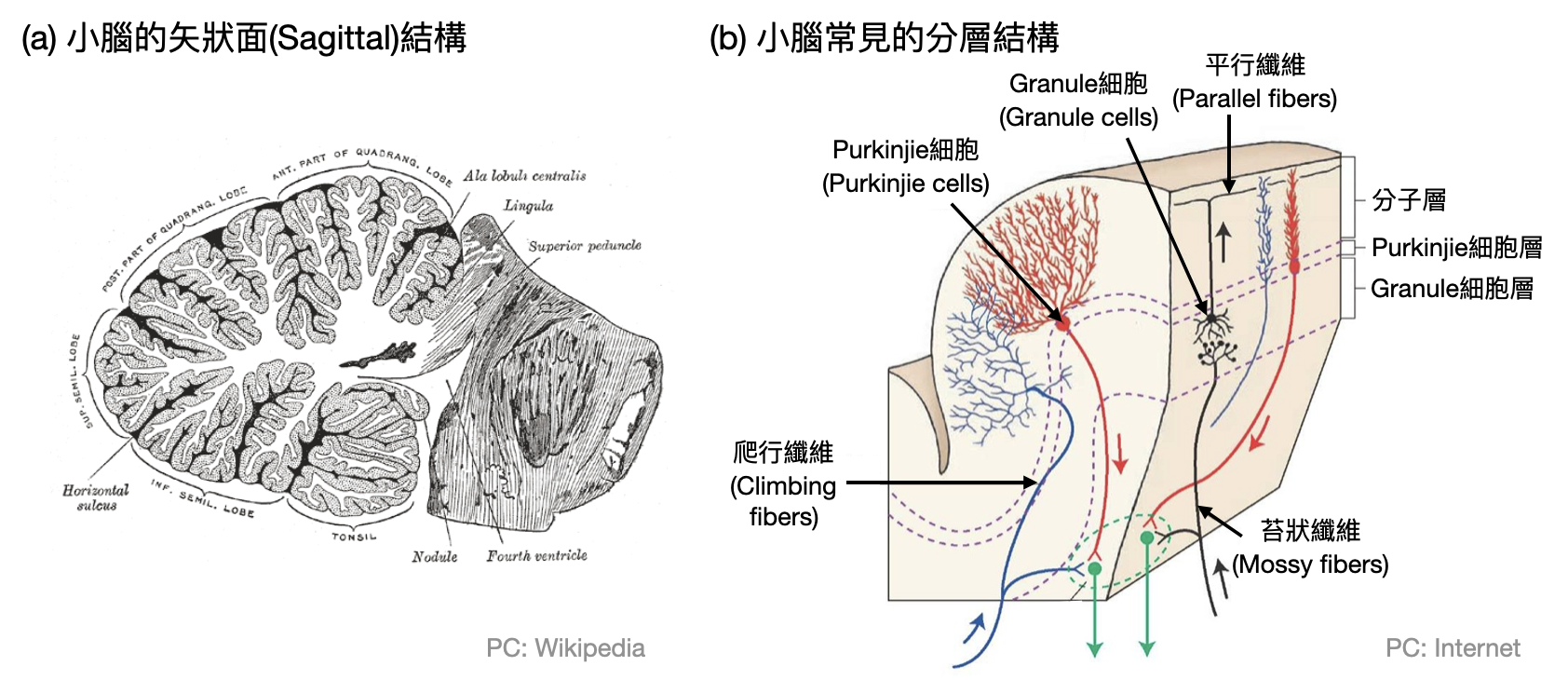
小腦(Cerebellum)大約只有拳頭大,位於大腦皮質顳葉和枕葉下方、腦幹上方。傳統上小腦和肌肉的控制與平衡有關,新的研究也漸漸顯示其和心情甚至是其他的認知功能(例如語言、注意力、想像力)息息相關。雖然小腦只佔整個腦的10%重量,然而其神經元個數和大腦不相上下。而且小腦的神經元種類比較單一,主要由Purkinjie細胞、Granule細胞和苔狀纖維(mossy fiber)組成三層“發散到收斂”的結構。
腦幹(Brainstem)將大腦連接至脊髓,進而將神經訊號傳遞至全身,同時調控許多重要的系統,例如呼吸、心跳等等。其主要結構為中腦(midbrain)、橋腦(pons)和延腦(medulla)。
現今主要的腦神經科學實驗技術
工欲善其事,必先利其器。在更進一步思考腦神經科學中的問題之前,讓我們先迅速地一覽常見的訊號錄製技術以及實驗中使用的模式生物(model organism)。
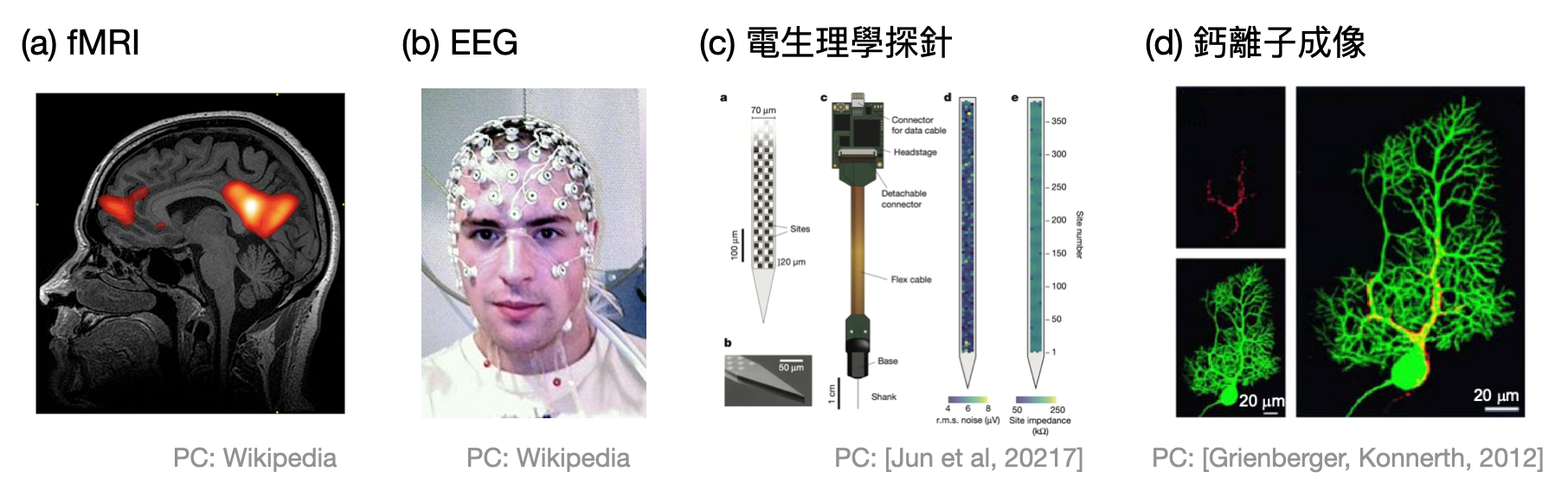
腦訊號錄製技術: 這個世界上目前還沒有完美的腦訊號錄製技術,現今常見的技術在不同層面各有漸長,例如訊號的解析度(在時間軸和空間軸上)、錄製的範圍、可允許的實驗設計、設備的價錢、操作的困難度等等。以下介紹的四大類技術,在回答不同研究問題時各有千秋。或許在不久的將來,腦神經科學中也能夠出現像大谷翔平一樣投打雙棲的錄製技術?
- 功能性磁振造影(fMRI, functional Magnetic Resonance Imaging)也許是最為人所知的腦訊號錄製技術。類似在健康檢查自費項目常出現的MRI磁振造影以及電腦斷層(CT, Computed tomography)和正子斷層掃描(PET, Positron Emission Tomography),這些技術的共通點都是能夠一次擁有大範圍且在空間軸上對大腦的活動有很高的解析度,不過通常在時間軸上的解析度不佳。而且fMRI是紀錄腦中血流的變化,雖然這和神經元的活動相關,但由於不是直接和電訊號有關,所以在解讀結果時要格外注意。
- 腦電圖(EEG, Electroencephalography)就是出現在電影或動畫中,將人(或猴子)頭上放滿電極裝置的錄製技術。EEG透過在頭皮表面測量電位差,獲得腦中各種訊號。然而就像在假日的公園外走一圈時,可以聽得到許多人玩耍嬉鬧的聲音,但是很難明確的區分各個聲音的來源為何。雖然EEG的解析度仍然不高,不過相較fMRI起來能夠獲取較多的時間軸訊息及電訊號,因此較適合用來分析大尺度上神經活動的差別,例如在早期EEG常被拿來分析受試者的睡眠狀況。
- 電生理學(Electrophysiology)技術透過侵入式的探針(probe),直接將電極擺放在腦神經元附近並測量其電訊號的活動。根據不同的具體技術,有些能夠針對單一神經元做到極為精細的測量,有些則是著重在較大範圍(數百數千個神經元)因而喪失些許的空間軸解析度。從錄製到的訊號中,可以再依照頻率的高低做不同的分析:高頻率(>500赫茲)的訊號對應到某個神經元的動作電位,低頻率(<300赫茲)的訊號則和周邊許多神經元的電位有關,又被稱為局部場電位(LFP, Local Field Potential)。電生理學錄製技術可以說是腦神經科學實驗中最主要的工具。
- 鈣離子成像(Calcium imaging)首先利用基因技術,使某些類型的神經元將會在內部具有鈣離子指示劑(calcium indicator)。接著,當這些神經元活動時,其內部的鈣離子濃度會急劇上升,只要在紫外光照射的之下,便會和鈣離子指示劑產生反應發出瞬間的螢光,並且被特殊的螢光/雙光子顯微鏡記錄下來。雖然其解析度通常略遜電生理學技術,不過在研究不同神經元類型時,鈣離子成像透過基因技術便可以很精準地只觀測某種類型的神經元。
模式生物: 不僅僅是因為倫理關係而不在人身上做腦神經科學實驗,很多時候更是為了先從規模較小的生物體中,建立對某些腦機制更好的認識。模式生物就是指在領域內被公認適合來研究特定機制的生物種類。腦神經科學常見的模式生物有:海蝸牛(Aplysia)、果蠅、斑馬魚(zebrafish)、各種鼠類(小鼠(mouse)、大鼠(rat)、沙鼠(gerbil))、獼猴(Macaque monkey)等。
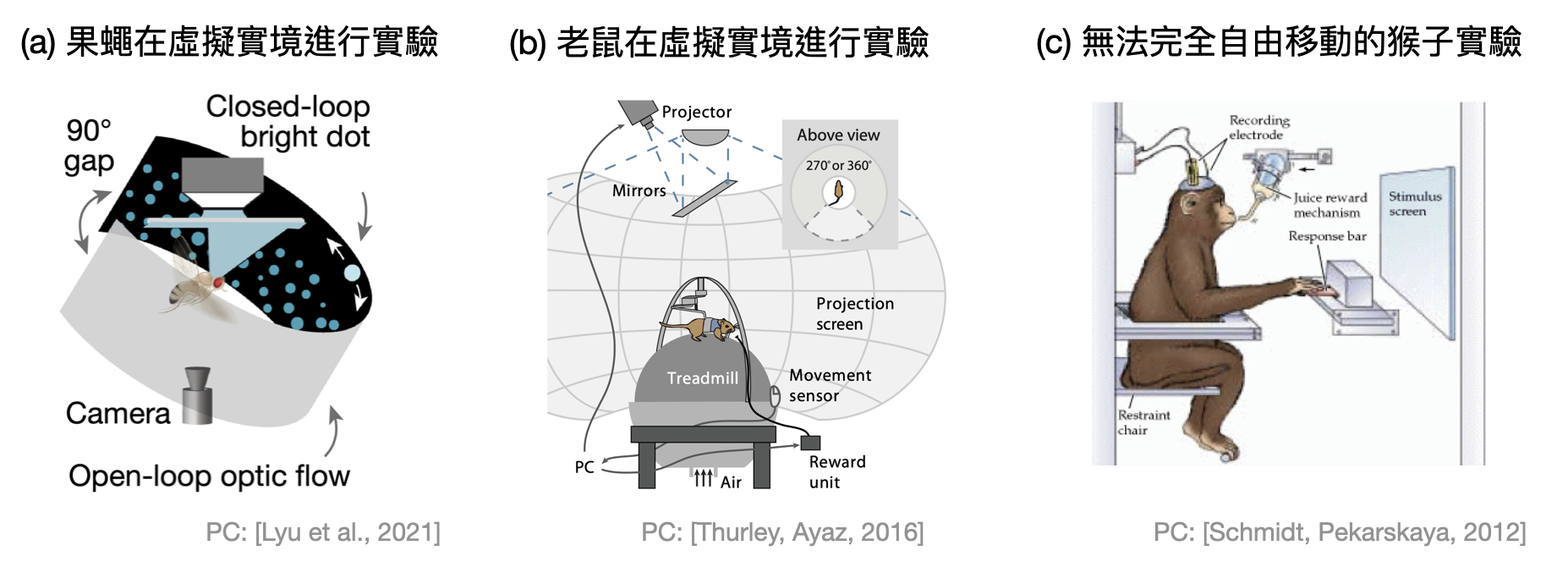
在實驗中,也不是總是會讓這些動物到處亂跑(free-moving)。根據不同的需求,有時候會固定頭部(head-fixed)、麻醉(anesthetized)等等。近年來由於電腦科技的進展,許多實驗室也引進了虛擬實境的技術,讓動物們站在一顆球上,探索著眼前螢幕呈現的虛擬世界。
一趟腦神經科學與計算的小獵犬號之旅
希望到目前為止建立的大方向圖像,能讓讀者有足夠的基本概念及興趣,繼續探索更多腦神經科學與計算之間有趣的關聯。在剩餘的篇幅中,我們將從單一神經元開始,慢慢往上拉高層次,欣賞九個不同的主題,航向屬於我們的“小獵犬號之旅”。
單一神經元與Hodgkin-Huxley模型
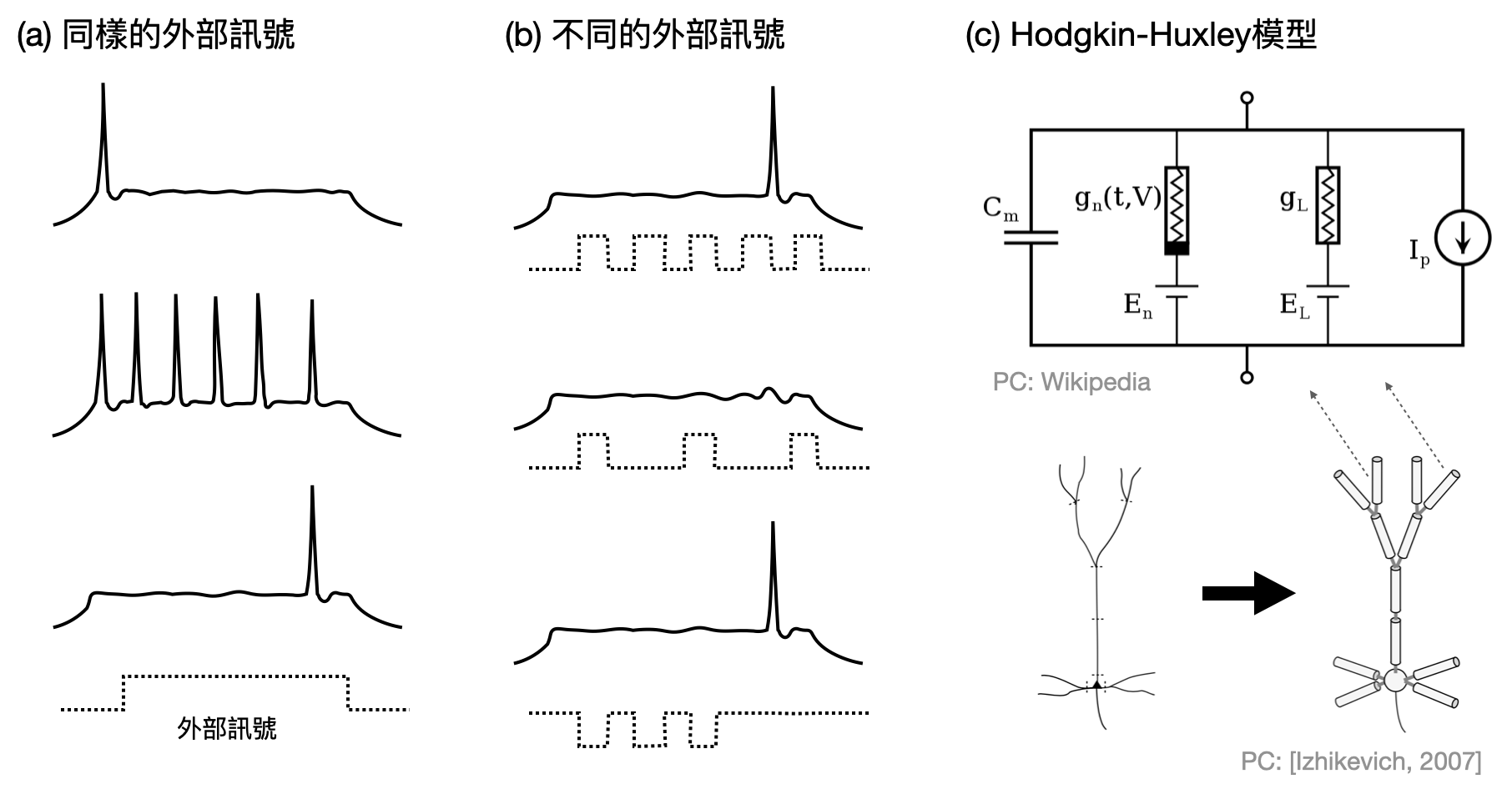
在這個全球化與工業化的世代,時常會聽到評論家比喻每個人在社會中的角色像個小螺絲釘一樣,雖說如此,不同職業和崗位做的事情可是可以非常不一樣的。對於千億分之一的神經元也是如此,不同的神經元類型或是不同的連接結構,將會讓神經元的電脈衝方式、規律、時間點很不一樣。每個人都是天底下獨一無二的存在,每個神經元是否也在腦中扮演著獨特的角色?
這麼多樣多變的神經元活動方式(如下圖(a)和(b)),該不會各自是從很不一樣的機制產生,需要逐一建模型理解吧!?Alan Hodgkin(1914-1998)和Andrew Huxley(1917-2012)告訴我們有一個數學模型(以及一些簡單的變形)可以用簡單的方式描述絕大多數的現象!為了紀念他們的貢獻,這個模型又被稱為Hodgkin-Huxley模型(如下圖(c))。這些對神經元基本性質開創性的研究,也讓他們在1963年共同獲得了諾貝爾生醫獎。
不同行為的神經元,可能扮演著什麼樣不同的計算角色呢?
突觸可塑性與學習
新認識的朋友如果時常一來一往的傳訊息聊天,很快就能熟絡起來。許久不見的老朋友只需一通長途電話,當年的回憶就會湧上心頭。人與人之間的關係是可以透過經營而加強或是減弱的,對於神經元來說也是如此。
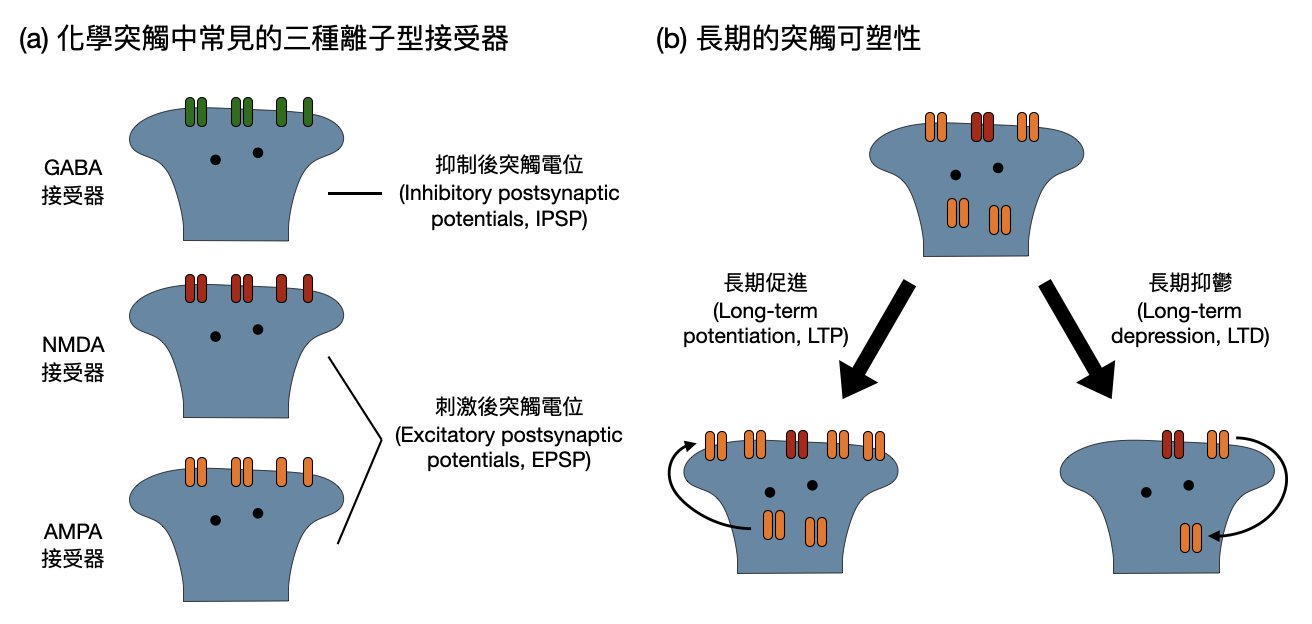
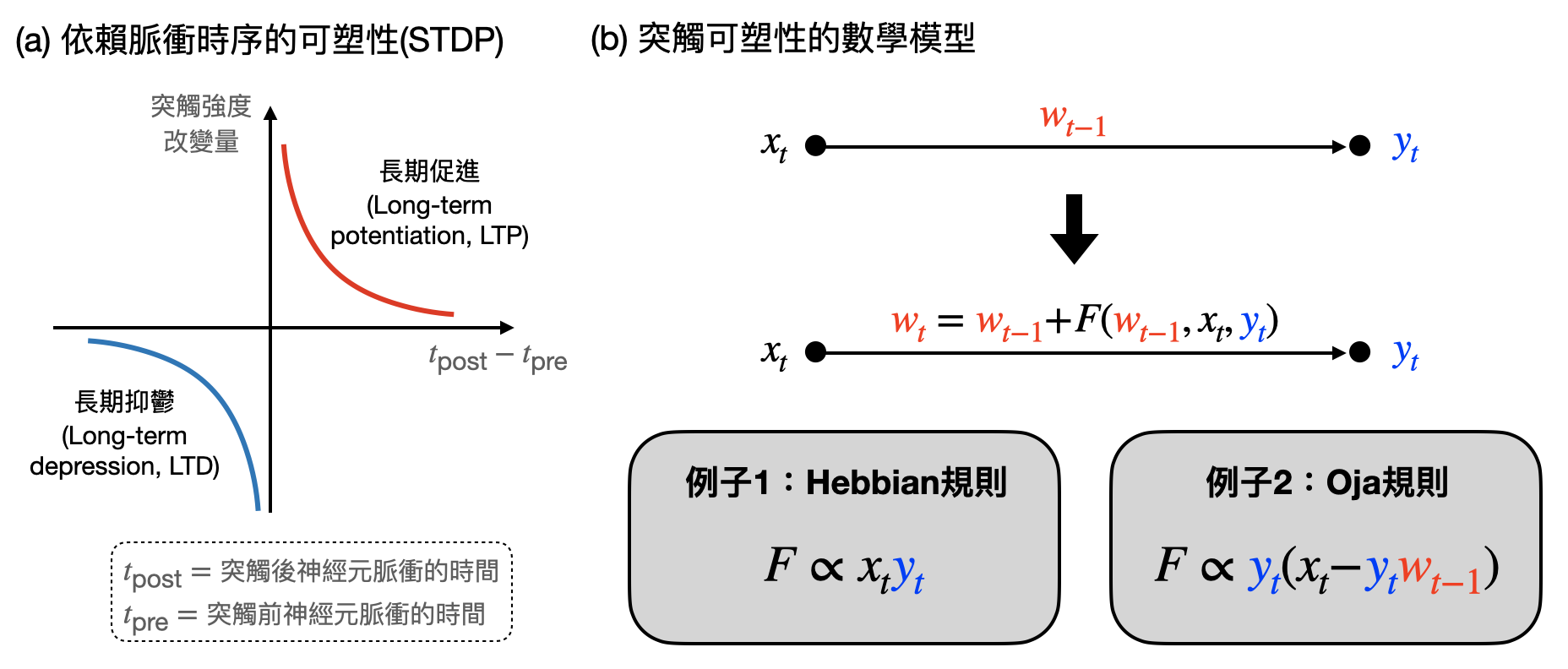
神經元間突觸的強弱變化,被稱為突觸可塑性(synaptic plasticity)。除了之前提到的長期促進(LTP)和長期抑鬱(LTD)之外,腦神經科學家還觀察到許多其他突觸強度改變的機制(例如下圖(a)中的STDP)。理論學家也提出了不少數學模型,試圖探索突觸可塑性和神經網路所進行的計算有什麼關聯(如下圖(b))。如果你的朋友總是秒回訊息,是不是代表你們更親近一些?如果互動太過頻繁,是不是該稍稍冷卻一下保持一點距離?
如果不只考慮一個神經元和其他神經元的連結,而是整個神經網路中神經元兩兩之間的突觸強度是如何變化,該怎麼建立與理解突觸可塑性和計算的關係?在抽象層面上,由於一個神經網路就像是個計算過程(例如將感知輸入對應到動作輸出),突觸可塑性就像是“改變計算過程的計算”。因此,很自然而然地被和“學習”(詳見本書第三章後半部分)連結了起來。透過設計和分析不同的「突觸可塑性規則(synaptic plasticity rule)」及潛在/相對應的計算問題/原則,會不會讓我們對腦中的底層實作有更模組化的理解?
在人工神經網路的世界中,「反向傳播法(backpropagation)」是個極為成功的人工突觸可塑性規則,其主要概念是透過微積分的鏈鎖率(chain rule),算出每個突觸的強度該如何變化,可以最有效率的提升整體的準確率。雖然反向傳播法在人工神經網路與人工智慧取得前所未有的進展,但是由於生物條件的限制(例如特定的突觸連結方式),普遍來說腦神經科學家們認為大腦的學習方式應該與反向傳播有點距離。到底我們的腦子是如何學習的呢?透過細緻地理解突觸可塑性能夠幫助我們釐清學習的本質嗎?
感受場與調諧曲線
不知道你有沒有想過相機和眼睛的運作有什麼差別嗎?透過相機鏡頭的發散與聚焦,外在世界的光打在感光元件上,由於每個感光元件各自對應到不同地方傳來的光,最終它們根據光的強弱記錄下瞬間的永恆。我們的眼睛是怎麼運作的呢?也是用類似的方法嗎?
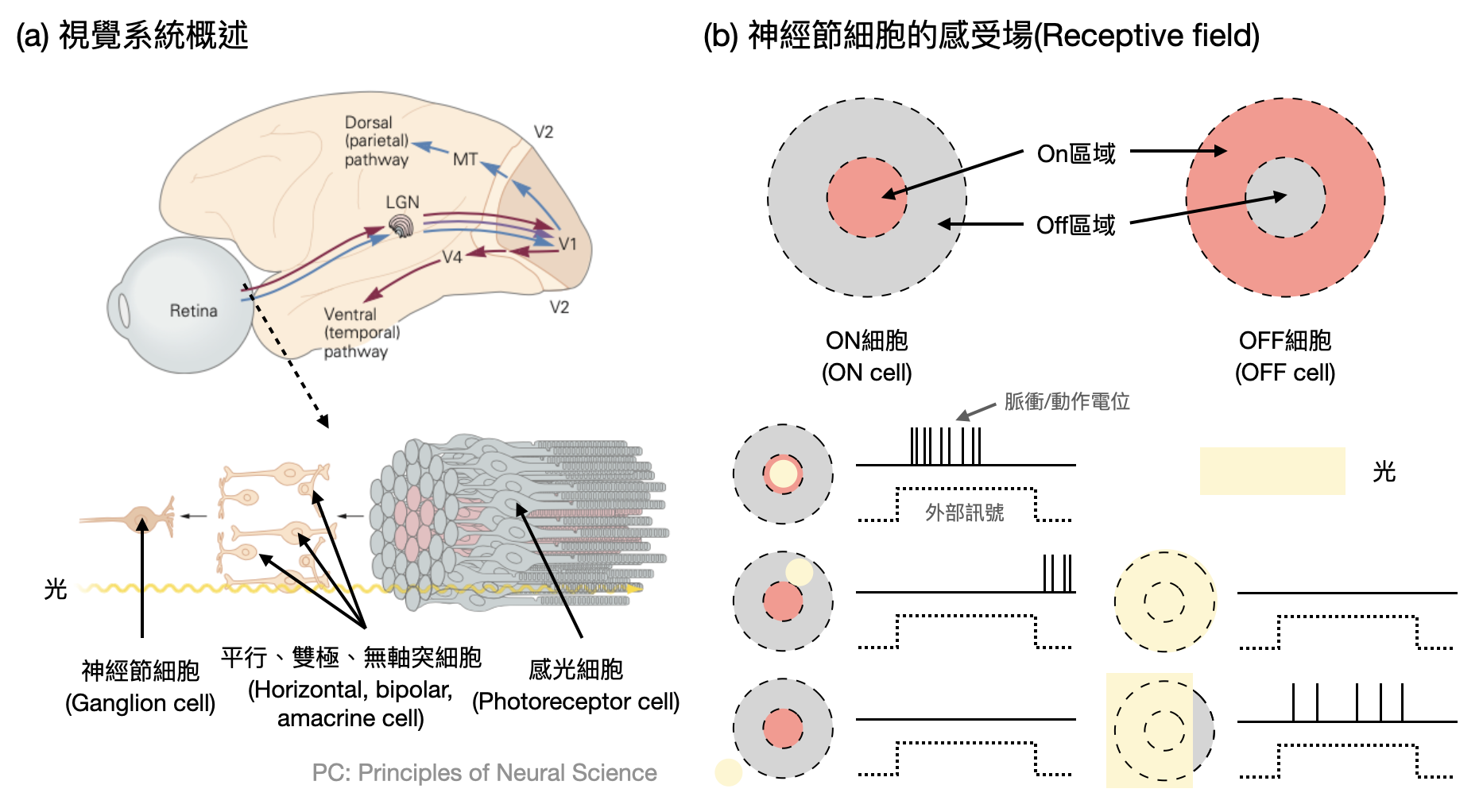
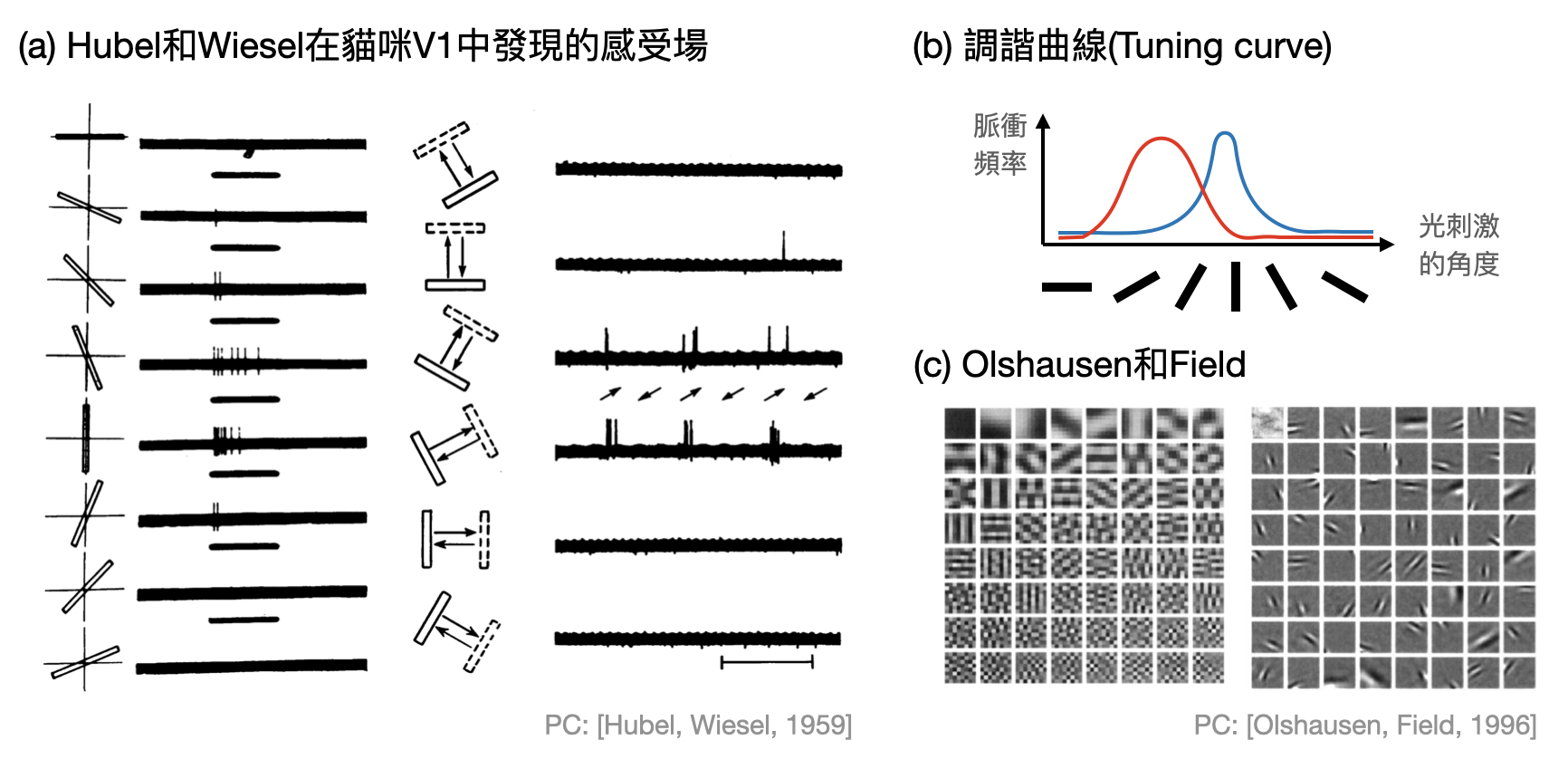
眼睛中主要的神經區域為視網膜(retina),其中的第一道關卡「感光細胞(photoreceptor cell)」的確就扮演著類似於相機中感光元件的角色,每個感光細胞各司其職關注著世界的某一個小角落。然而,當更深入視網膜的神經網路,甚至是進入大腦皮層的視覺相關區域後,事情將會變得更加有趣:神經元不再只是關注某個小角落光的強弱,而是開始對某個區域的特定圖案產生反應。就像一座監獄的守衛們,各自看管某個區域的動靜,並且只會針對可疑的騷動做出反應。於是,對於一個視覺神經元來說,這樣會讓它特別有反應的區域和相對應的圖案,又被稱為它的「感受場(receptive field)」(如下圖(b))。
大腦皮層中第一個和視覺相關的區域被稱作「主要視覺皮層(V1, primary visual cortex)」。1959年,David Hubel(1926-2013)和Torsten Wiesel(1991-1998)在他們著名的實驗中,日以繼夜地嘗試不同的視覺圖像給貓咪看,希望能夠釐清V1中神經元的感受場。一開始他們試著將光點擺在不同的位置,看看神經元會不會對特定的位置有反應,但是事與願違。直到後來他們才發現,許多V1的神經元對於一條線狀的光源特別有反應,另外還有一些神經元則是當一條線以某個角度往某個方向移動的時候會有劇烈反應,也就是說,V1神經元的感受場是呈線狀的,而且可能還會跟時間軸有關!這個重要的發現以及他們後續在視覺系統上重要的貢獻,也毫不意外地讓他們在1981年獲得了諾貝爾生醫獎。
在V1中每個神經元關注的角度可能不太一樣,而且即使是同一個神經元,可能也會對接近感受場的角度發出一些脈衝。因此,「調諧曲線(Tuning curve)」的概念就應運而生了:對於某個神經元(以V1中的神經元為例),根據其對於不同輸入刺激的參數(例如光刺激的角度),畫出相對應的脈衝頻率函數。如此一來,根據調諧曲線就可以看出某個神經元是如何“編碼(encode)”某個角度(如下圖(b))。
通常在知覺系統中的神經元,尤其離輸入端越近的,都可以被觀測到具有明顯的感受場,並可以畫出其調諧曲線。在這些概念的輔助下,我們可以更進一步用很計算的角度來揣測這些神經元以及相關的腦區是如何處理感官輸入的:每個神經元的感受場就像是對應到了字典中的一個字,當眼睛接受到一個畫面後,有反應的那些視覺神經元就像是告訴接下來的腦區這個畫面出現了什麼字。那麼大腦是用什麼樣的字彙和語言來溝通的呢?
舉例來說,Bruno Olshausen和David Field在1996年引入「稀疏編碼(sparse coding)」的觀點,利用數值實驗試圖論證感受場的形狀是源於大腦希望神經元的反應比較稀疏(如上圖(c))。以字彙和語言的比喻來看,等於是在說希望能夠用簡單幾個字就可以表達看到的東西。這個前衛的學說也間接開啟了電腦科學中「字典學習(dictionary learning)」的發展。
然而對於越深的腦區,我們知道的越來越少。不知道感受場、調諧曲線這些單一神經元的分析,能帶我們走多遠?
導航、位置細胞與網格細胞
想像你來到了一座新的城市,手機尚未連接上網路,因此沒辦法使用線上地圖。由於語言不通,又無法向路人問路或是買地圖。但是一直待在旅館實在太無聊了,於是你決定到外頭晃一晃,想說有著太陽的幫助,應該總能在天黑前回到旅館吧?踩著陌生的街道,映入眼簾的是有如天書一般的商店招牌,雖然看不太出來他們到底是在賣什麼,不過你已經對某些不斷重複出現的連鎖店開始有些印象了,也許那個有著鮮紅色招牌的店家是個便利商店、藥局或速食餐廳?
不只是對來異境旅遊的旅客,導航對生活於大自然中的動物們也是非常重要。大腦是如何引導螞蟻外出覓食後找到回家的路?Monarch蝴蝶會經過好幾個世代從墨西哥遷徙到北美,它們是怎麼做到的?背後又有什麼計算的原理支撐著?
在這邊讓我們透過受到2014年諾貝爾生醫獎認證的「位置細胞(Place cell)」與「網格細胞(Grid cell)」,一窺腦中的迷航世界。
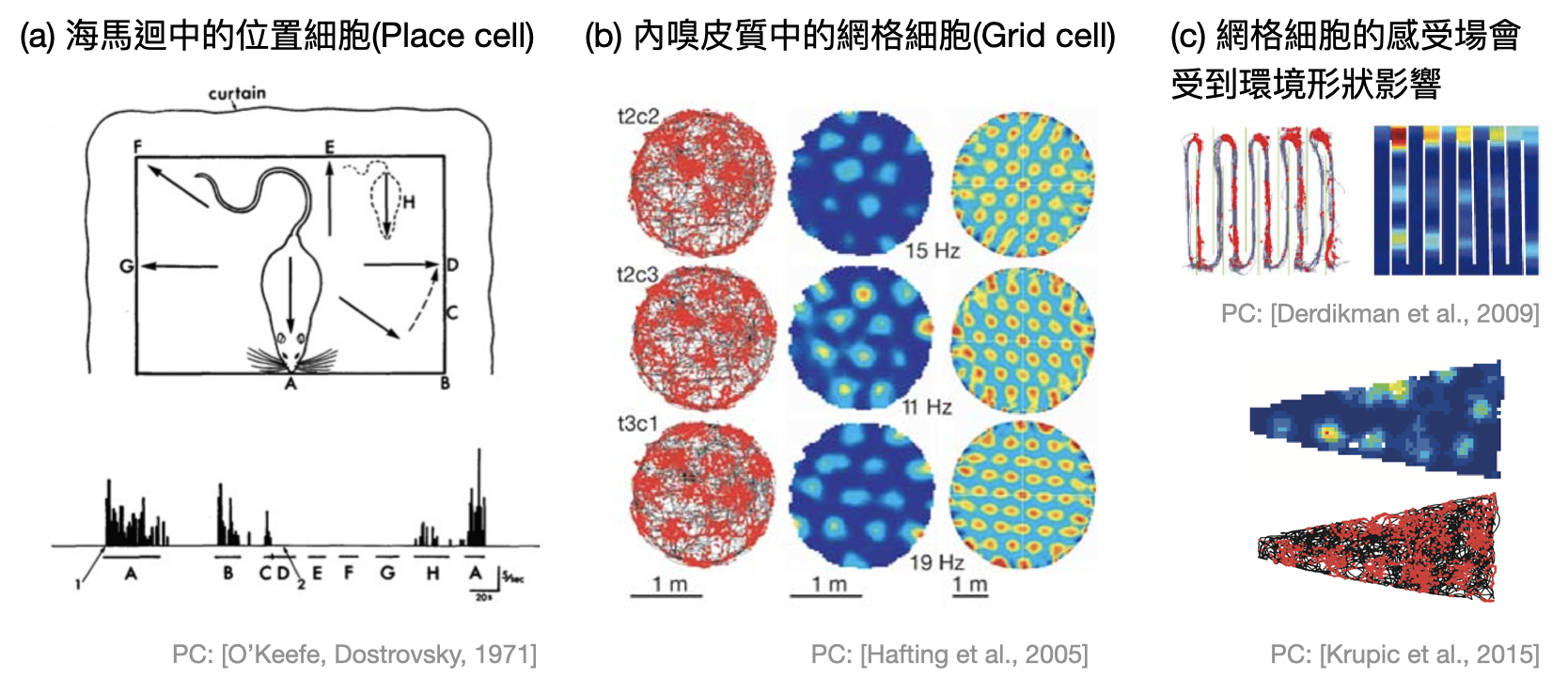
John O’Keefe是個受心理學訓練出生的腦神經科學家。和多數心理學家一樣,O’Keefe十分重視動物行為扮演的角色,因此當他從在博士期間主要研究的杏仁核轉移到海馬迴時,他首要關注的就是海馬迴受傷的小鼠會有什麼樣異常的行為表現。很快的,他和學生們就發現這樣的小鼠在進行空間相關的任務時,表現得特別差,尤其是當轉移到新環境之後。經過更深入的實驗,他們發現海馬迴中的CA1區域具有一些特殊的神經元,會在小鼠經過某個特定的位置時有劇烈的反應(如上圖(a))。這種類型的神經元因而得名“位置細胞”,並開啟了腦神經科學界對海馬迴在導航與記憶中所扮演角色的探索。
Edvard Moser和May-Britt Moser是諾貝爾獎史上第五對共同獲獎的夫妻。完成博士學位後,兩人輾轉來到倫敦在O’Keefe的麾下學習了一陣子,接著回到家鄉挪威建立自己的實驗室。深受位置細胞的啟發,兩位Moser決定追根溯源研究位置細胞是如何形成的。從神經元連結的解剖資料中,他們與學生們嘗試了相關的腦區,最終在2005年發現內嗅皮質(entorhinal cortex)中有許多特別的神經元,會根據小鼠所在的位置極其規律的產生反應。如果小鼠所處的是個方形空間,這種神經元相對於小鼠位置的感受場,將會近似於一個正三角型網格的網格點(如上圖(b)),於是得名“網格細胞”。
所以我們可以將腦中的導航想成有著網格細胞建立地圖的經緯,再由位置細胞紀錄重要的地點嗎?很可惜這樣的圖像有點過於簡化,生物世界中的例常就是總有例外。以位置細胞來說,實驗上可以觀測到當小鼠更換環境之後,感測的位置也會跟著變動,因此被稱為「重新對應(remapping)」。如果改變環境的形狀,網格細胞的感受場也將失去正三角型網格,變成其他種規律的網格(如上圖(c))。
位置細胞和網格細胞是少數在大腦比較深的區域中,仍然具有清晰感受場的神經元類型,因此有著大量的研究工作圍繞在理解它們的成因和特性。然而大腦中的導航更像是個動態的地圖,並且和其他的功能(例如記憶)息息相關,我們仍還有很長的一段路要走。
多巴胺神經元與獎勵預測
平時常常會聽到人們提到多巴胺(DA, dopamine)的分泌會帶來快樂感,你知道多巴胺是種腦神經傳導物質嗎!?而那些會釋放多巴胺的神經元又被稱為多巴胺神經元(dopaminergic neuron),主要分佈在中腦(位於腦幹)的腹側被蓋區(VTA, Ventral Tegmental Area)與黑質(SN, Substantia Nigra)以及下丘腦等區域。
在James Olds(1922-1976)和Peter Milner(1919-2018)於1950年代進行的著名實驗中,他們將一些電極插入小鼠部分的腦區,並且當小鼠推動一個桿子時注入電流觸發腦區附近神經元的動作電位。他們發現當電極插在某個腦區時,小鼠會不斷地推動桿子,就算有食物、水、甚至是異性的吸引都無法轉移小鼠的注意力。如此明顯的行為關聯,讓他們決定仔細研究這塊腦區,並且發現此處大部分的神經元都和多巴胺神經元有連結!
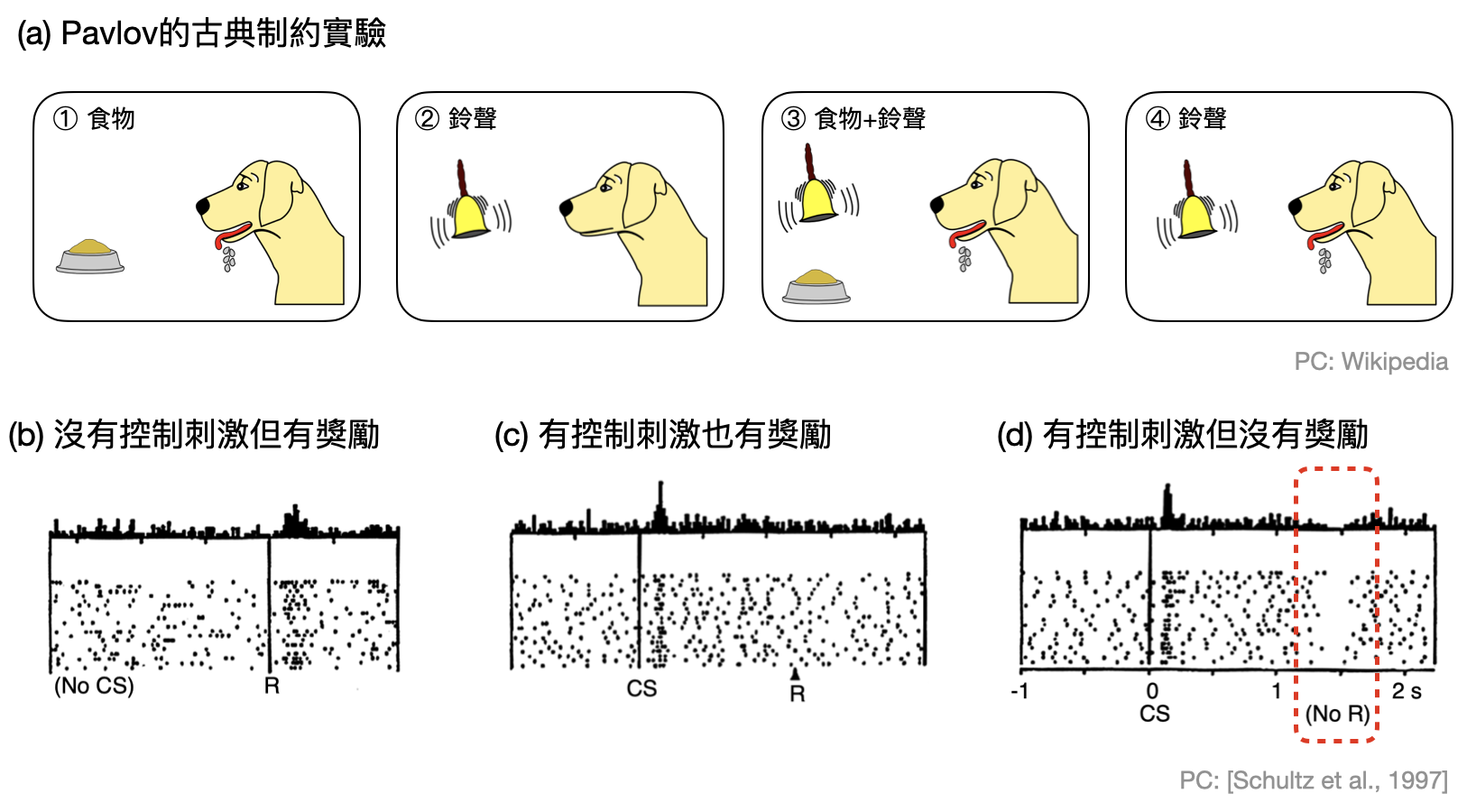
所以我們的腦中是由多巴胺神經元掌控快樂的泉源嗎?事情沒有這麼單純!在1990年代末期,Wolfram Schultz和合作者發現了多巴胺神經元不只會在獲得獎勵(在實驗中設計的快樂泉源)時會產生反應,一旦接受到了獎勵即將來臨的徵兆(例如聞到美食的氣味),多巴胺神經元就會開始躁動了。更令人驚訝的是,如果最後小鼠沒有獲得獎勵,多巴胺神經元的脈衝數量竟然會下降(如下圖)!
於是,多巴胺神經元的活動漸漸被認為和“獎勵預測”有關:如果預期心裡被滿足了,那麼多巴胺神經元就不會再特別活動。反之,如果預期落空,多巴胺神經元就像是透過減低活動量,來釋放“預測誤差”的信號。
近年來腦神經科學家對於多巴胺神經元有了越來越多細緻的研究,例如不同發訊號的模式或不同的細胞內活動都可能具有不一樣的功能,並且發現多巴胺神經元似乎也不僅僅只限於Pavlovian古典制約中的獎勵預測。也許,因為人類總是想著追求快樂,所以單純地將多巴胺和快樂劃上等號。但或許快樂並沒有單一源頭,更不見得是最後的終點。在思考多巴胺神經元的本質時,也許我們也會對快樂有了新的認識?
鳴鳥與聲音學習
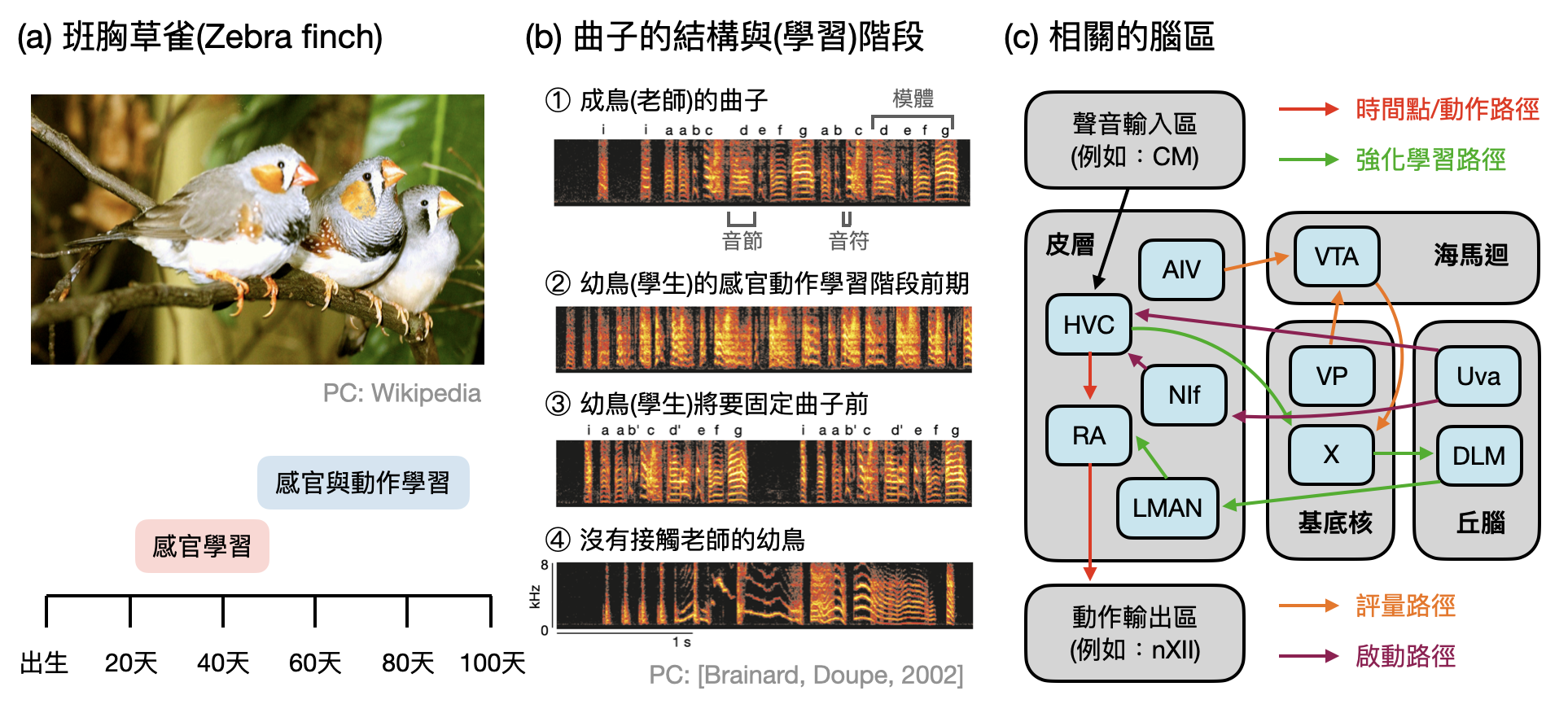
小嬰孩是如何從牙牙學語到發展出完整的語言能力?在嘗試回答這個重要但是極度困難的問題之前,也許我們可以先從生物世界中尋找類似但是簡單一點的模式生物作為起點。「斑胸草雀(zebra finch)」是一種具有厲害聲音學習(vocal learning)能力的鳴鳥(songbird),剛出身的小雀會在幾週內從沒什麼結構的唧唧喳喳(babbling),逐漸學會身邊老雀唱出來的曲子。
別小看鳴鳥們唱歌的能力,如何從胡亂的唧唧喳喳形成乾淨的音符(note)?如何在從音符的排列組合建立簡單的旋律模體(motif)?以及最後又如何組織不同的旋律模體形成完整的歌曲(如下圖(b))?腦神經科學家們在多年的研究之下,逐漸對這些步驟背後相對應的腦區及機制有了越來越清楚的認識。
從計算的角度來看,鳴鳥的聲音學習主要包含了三大元素:(1)聽覺系統的學習、(2)歌唱相關的肌肉動作學習、和(3)歌聲的評量以及改進。其中又以(3)最為複雜,下圖(c)中提供一個簡化的腦區線路圖讓讀者體會一下。
本書第三章曾經提到的強化式學習(RL),在鳴鳥聲音學習的研究中提供了許多靈感,一些腦區之間的行為和互動可以透過RL的架構和語言獲得直觀上的理解(如上圖(c))。不過RL當然還無法解釋一切,未來在剖析鳴鳥聲音學習系統的研究路上,說不定可以反過來提出新的計算/學習原則?
E/I平衡
之前我們學到了GABA是抑制型(inhibitory)的神經傳導物質(也就是說後突觸神經元在接收到脈衝後電位會下降),NMDA和AMPA則是刺激型(excitatory)的神經傳導物質(後突觸神經元在接收到脈衝後電位會上升)。一般來說,大腦中神經元的軸突不會同時具有多種神經傳導物質,於是一個神經元對其他神經元的影響,要嘛全都是抑制,要嘛全都是刺激,這又被稱為「Dale規則(Dale’s law/principle)」。
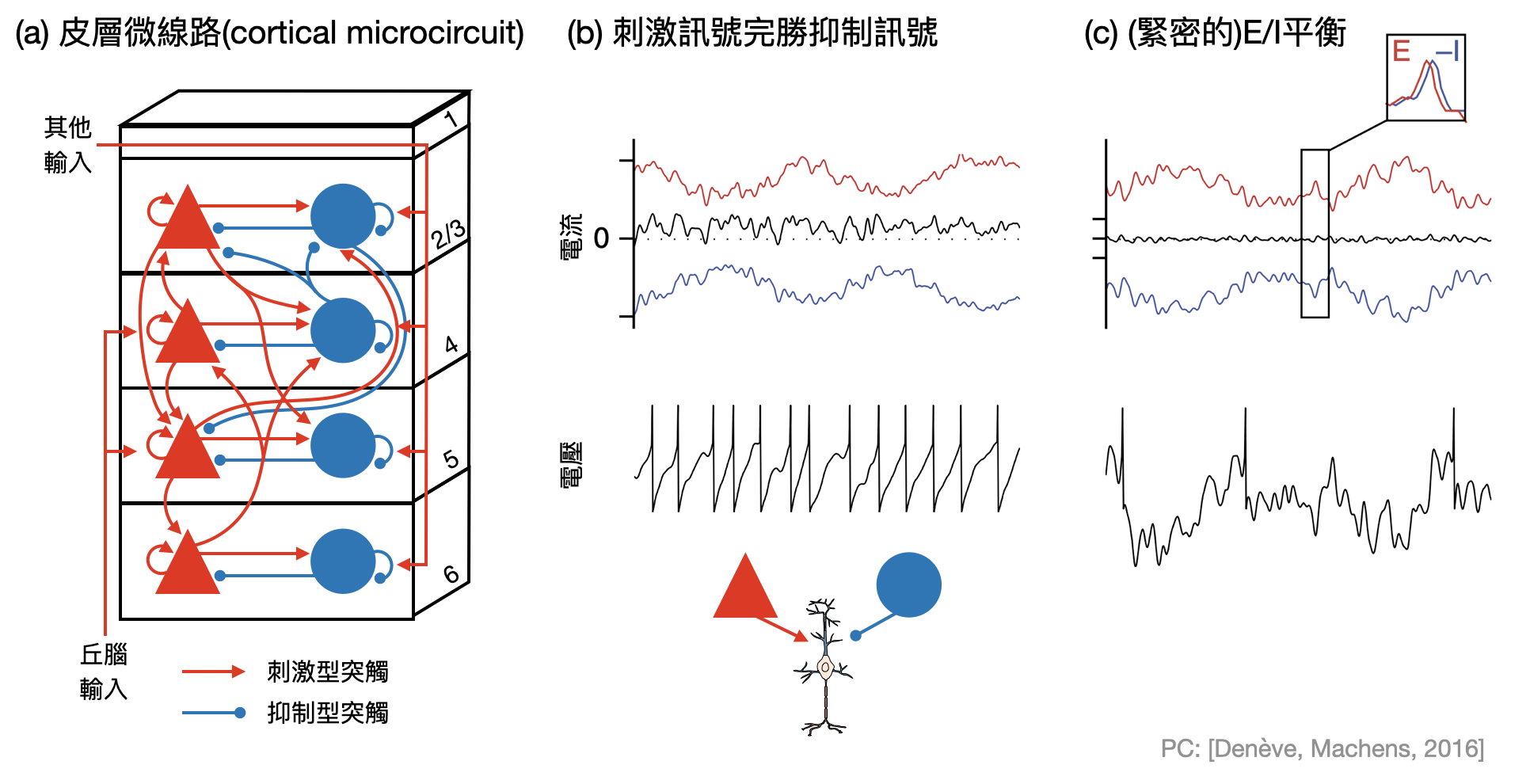
再更進一步,大腦許多區域(尤其是大腦皮層)的結構是非常有規則的,通常刺激別人的神經元和抑制別人的神經元會和同類型的神經元聚在一起。於是抽象上來看,可以將大腦皮層視為由一群一群刺激神經元和一群一群抑制神經元組成的區域。而當觀察大腦皮層中的一個神經元時,一些實驗發現其接收到的刺激和抑制訊號竟然極度平衡(如下圖),並沒有其中一方明顯勝過另一方。這個現象又被稱為「E/I平衡(E/I balance)」,其中E對應到“刺激(excitatory)”,I對應到“抑制(inhibitory)”。
目前為止,多數腦神經科學家將E/I平衡理解為能夠在訊息的編碼和傳遞上面帶來好處,例如透過刺激和抑制訊號緊密地互相追蹤,大腦能夠更加迅速的控制、改變與平衡訊號。也有些理論研究提出E/I平衡和沒有平衡比起來,能夠具有較大的訊息編碼的容量(capacity)。
刺激訊號和抑制訊號之間的對偶,也許有點像上漲的股票和下跌的股票,只有很特殊的情況才有可能滿江紅,多數時候總是努力試著讓上漲的超前於下跌的。載浮載沉於大時局的波浪中,什麼時候能夠看透其中的奧秘?
效率編碼假說
Horace Barlow(1921-2020)是位著名的視覺神經科學家,同時也是達爾文的外曾孫(他媽媽是達爾文的孫女以及傳記的作者)。從小在媽媽的薰陶之下,Barlow建立了扎實的數學及科學基礎,並且很早就投身科學研究(大學時就在Nature雜誌上面發表文章了)。在劍橋大學開放的學風下,Barlow得以自由選擇研究題目,並從青蛙的視覺Ganglia細胞出發,開啟了他日後輝煌的學術生涯。
早期的視覺神經系統研究可以說是環繞在分析不同的感受場,隨著知道越來越多種神經元的感受場,一個半科學半哲學問題便自然地浮現了:這些感受場的功能是什麼?為什麼視神經元的感受場是長這個樣子而不是其他的樣子?就像Barlow在他1961年的著名論文(詳見延伸閱讀)中開頭提到的例子:假設我們不知道鳥會飛,那我們再怎麼努力的研究翅膀的複雜結構,仍然會不知其所以然。感知系統的背後是被什麼樣的計算/功能原則支配著?
Barlow在同篇論文中,進一步給了三個假說,嘗試從Marr三階層分析中“計算理論”的角度指引人們對感知系統的研究與理解。其中的「降低冗餘假說(redundancy-reduction hypothesis)」被後世以更廣義的「效率編碼假說(efficient coding hypothesis)」流傳至今。既然都是由上而下的假說,在這邊我們將跟隨Barlow的文章著重在抽象的比喻,不討論具體的實驗例子。
讓我們將感知系統化簡為一個傳送訊息的通道,它受到一些生物上的限制(例如神經元連接的方式、生理循環條件、不確定因子造成的噪聲等等),目標則是要將有用的訊息傳送給其他系統(例如動作、整合、學習、記憶等系統)來使用。感知系統該如何“編碼(encode)”各種輸入的訊息(例如看到的景色、聽到的聲音、感受到的觸覺)呢?可以想像的是,如果將此想成一個工程上的問題,將會有非常多種可能的實現方式。然而以視覺系統為例,腦神經科學家在不同演化路徑上的模式生物中都發現了相似的感受場形狀。乍看之下,演化似乎很有規律地選擇了一些特定的方式來實現腦中的感知系統。
效率編碼假說對這個大哉問的回答很簡潔:感知系統將會使用“最有效率的方式”來編碼訊息。
通常當這樣抽象的大原則被提出,就會被認真地質疑和檢視其具體在生物世界中的對應和實現為何。什麼是“最有效率”?是用什麼樣的單位來計算?相關的生物意義是什麼?如此一長串的問題與辯論進行下去,再寫一本書都不為過。“效率編碼假說”至今仍然是(理論)腦神經科學界火熱的概念,只不過對於每個研究者來說,他們心中想的定義可能都略有不同。
所以讓我們悄悄地避開這些在前線關於細節的爭辯,回到Barlow1961年論文,看看他最後的一段話:「盲目地研究感知系統將是愚蠢的,人們必須仔細看看動物是怎麼利用它們的感官系統。」就算效率編碼假說不是終極的回答,透過這樣計算的視角,我們得以有個著力點踏出詢問生命意義的一小步。
預測編碼假說
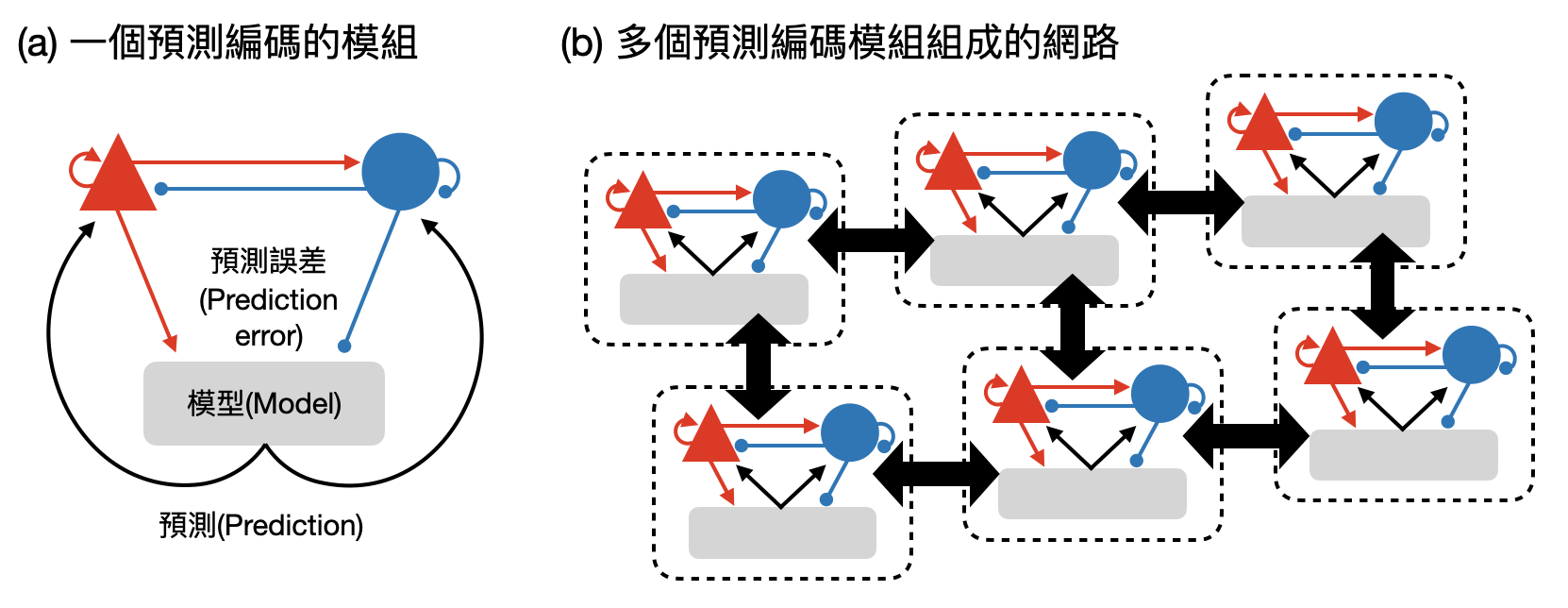
效率編碼假說推崇大腦會用最有效率的方式來編碼訊息,同樣廣受歡迎的「預測編碼假說(predictive coding hypothesis)」,則更進一步猜測腦中不同階層的區域會透過“預測(prediction)”以及“預測誤差(prediction error)”的訊號來更動其編碼方式,藉此提高效率。
想像你在大公司或是公機關擔任小職員,當客戶上門時,如果他的需求在你預期可以處理的範疇之內,那麼你就會不用麻煩其他人,自己就可以解決。然而如果遇到你無法處理的狀態時,你可能會趕緊向小主管求救,希望見過比較多大風大浪的他,能夠預期如何處理這種突發狀況。如果仍然不見效,你們可能會一起彎著腰去跟大老闆求助,如此往上報直到問題解決。
和上述的故事很相似,預測編碼假說提倡不同腦區和層次會各自維持一個“模型”,模型會根據各種感知輸入和其他區域給的訊息,產生對輸入訊號的預測。一旦預測錯誤,便會用預測值和實際輸入訊號的差異來更改模型。在接近感知系統初期的腦區(例如V1的皮質柱),可以各自負責建立模型預測不同範圍的低階感知訊息。處於高階的腦區(例如深層的視覺皮層)則負責建立比較抽象的高階層模型。如此一來,效率編碼假說中想要尋找的“計算目標”,便可以是“降低預測誤差”。
從之前多巴胺的例子中,我們已經看到多巴胺神經元扮演著類似“獎勵預測誤差”的例子,Rajesh Rao和Dana Ballard也在他們1999年經典的論文中嘗試用預測編碼假說來解釋感受場的一些性質。簡單總結來說,效率編碼假說和預測編碼假說,在過去幾十年中讓腦神經科學家有了一套“計算的語言”,得以深入的分析和理解在實驗中觀察到的現象。在未來,我們是否能夠擴大它們的詞彙庫,並且讓高層次的理論與低層次的生物實作細節有更多的連結?又或是能夠有其他的計算原則/假說能夠引領腦神經科學步入下一個階段?
總結
腦神經科學是個既和我們自身相關、豐富有趣又充滿可能性的一個主題。對於之前沒有接觸過太多相關知識的讀者,希望本章的內容能夠激起你進一步學習的基礎和熱忱。而對於領域內的讀者,也希望本章的編排及敘事角度能夠帶給你新的啟發。
雖然計算的工具和概念在近年來開始被大量使用在腦神經科學的各種研究中,但是“用計算的思維來認識大腦”這個角度則是才正要萌芽。筆者私認為“計算”是人類在進行“機械與邏輯化思考”時,最舒服和最能夠建立共識的形式語言。不過如何建立一套“計算的語言”以及相對應量化的分析技術、實驗設計、以及理論的架構和詮釋,仍然還要走一段漫漫長路。
透過本書十個橫跨數學、物理和生物的章節,希望讀者能從中獲得感官和知識上的享受,在酒酣耳熟之際,也可以細細咀嚼每道菜背後的醍醐味。
延伸閱讀
教科書與其他教材:
- E. R. Kandel, et al. Principles of neural science. Vol. 4. New York: McGraw-hill, 2000.
- F. R. Amthor, et al.Essentials of Modern Neuroscience Eds. McGraw Hill, 2020
- E. M. Izhikevich. Dynamical systems in neuroscience. MIT press, 2007.
- P. Dayan and L. F. Abbott. Theoretical neuroscience: computational and mathematical modeling of neural systems. MIT press, 2005.
內文引用的論文:
- A. Citri and R. C. Malenka. Synaptic plasticity: multiple forms, functions, and mechanisms. Neuropsychopharmacology, 2008.
- J. Dapello, Joel, et al. Simulating a primary visual cortex at the front of CNNs improves robustness to image perturbations. Advances in Neural Information Processing Systems, 2020.
- D. Sussillo. Neural circuits as computational dynamical systems. Current opinion in neurobiology, 2014.
- A.Mathis, et al. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nature neuroscience, 2018.
- D. H. Hubel and T. N. Wiesel. Receptive fields of single neurones in the cat’s striate cortex. The Journal of physiology, 1959.
- B. A. Olshausen and D. J. Field. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 1996.
- J. O’Keefe and J. Dostrovsky. The hippocampus as a spatial map: preliminary evidence from unit activity in the freely-moving rat. Brain research, 1971.
- T. Hafting, et al. Microstructure of a spatial map in the entorhinal cortex. Nature, 2005.
- W. Schultz, P. Dayan, P. R. Montague. A neural substrate of prediction and reward. Science, 1997.
- H. B. Barlow. Possible principles underlying the transformation of sensory messages. Sensory communication, 1961.
- R. P. Rao and D. H. Ballard. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature neuroscience, 1999.
- S. Denève,and C. K. Machens. Efficient codes and balanced networks. Nature neuroscience, 2016.