Chapter 1
Using Mathematics to Understand Computation
If we understand an idea then it is only by mathematically recreating it.
Misha Gromov
What comes to mind when you think of mathematics? For many, it’s homework problems like multiplying 57 by 28, factorizing 1038, or finding the solutions to $x^2-7x+10$. It’s not an exaggeration to say that countless children around the world begin to hate mathematics from the moment they are first asked to perform these types of calculations. What if I told you that these calculation exercises don’t truly represent what mathematics is about? What if I said that mathematics is not much different from writers crafting stories or musicians composing music?
Why is mathematics so closely associated with calculations in the minds of the general public? Upon closer examination, it becomes not surprising that mathematics and calculations, or more broadly speaking, computation, are indeed intricately connected. Computation acts like the grammar and rules for mathematical thinking. Can you imagine reading a novel without grammatical constraints or listening to a piece of music without any structure? Similarly, mathematics provides the semantics and syntax that make computations useful to us. Consider the 18th century, when people realized that steam could provide energy; they designed engines that converted this resource for various purposes, such as powering trains. In a similar way, the language of mathematics played an analogous role in the 20th century, transforming the abstract concept of computation into various kinds of computers that pervade our daily lives.
In this chapter, I will tell you the story of how mathematicians transform the abstract workhorse of computation into the machinery that we use everyday, much like how natural language describes the thoughts in our brains and music expresses the emotions we feel. What mathematics further offers is the ability to prove the limits of what can and cannot be computed. As we cannot predict if there will ever be a novel superior to Harry Potter or a musician greater than Beethoven, we can nevertheless be certain, within the black and white world of mathematics, that there are numerous problems humanity cannot compute.
Mathematics as a Rigorous Abstract Formal Language
In human society, the transmission of messages, the recording of knowledge, and communication between people are all based on various “languages.” Whether it is Chinese, English, or any other language, at its core is a set of abstract symbolic systems consisting of characters (and pronunciations), syntax, and semantic rules, among others. For those who know more than one language, you might have experienced this: in some situations, Language A might express thoughts more fluently, while in other scenarios, Language B feels more natural. This means that even though different languages can express what you want to say, sometimes one language seems to convey ideas more aptly than others.
Similarly, mathematics is also a language. In some cases, mathematics can express and communicate more effectively and precisely than other natural human languages.
How do you find patterns and devise profit-making strategies on the casino table when you want to make a big win? Naturally, the theory of probability comes into play. When you want to design an innovative house without it collapsing, geometry and trigonometry wave at you from around the corner.
From these examples, we can see that mathematics, as a language, is particularly adept at abstracting the similarities behind different things and concepts, and it has a very precise and rigorous structure. Once you accept a few basic axioms and reasoning rules in the world of mathematics, every theorem derived is a “truth” within this abstract world. While people often argue incessantly over usage and understanding discrepancies in everyday language, the clear-cut nature of the mathematical world is undoubtedly why many young scholars are drawn to its profound beauty.
With that said, I hope to have persuaded the reader to consider mathematics from the perspective of a “language,” viewing it as an abstract formal language, rather than just annoying problems on exams. Indeed, in many cases, the pursuit of perfection and rigor in mathematics can intimidate many. However, a truly good mathematical theory actually expresses complex matters in a clearer way. In the following sections, we will see how predecessors used mathematics as a formal language to abstract and axiomatize the seemingly complex and vague concept of “computation,” even opening up a whole new field: computer science.
Analog and Digital Signals
Before constructing the mathematical theoretical framework of computer science, we first need to decide on the foundational symbols, language, and units. In other words, how should we represent the objects we want to describe? What kinds of operations/calculations are possible? For instance, consider a 100-meter racetrack: how would we represent a runner’s current position? The starting point is 0, the endpoint is 100, one-third of the way is 33.3333, and three seconds after the start, the runner’s position might be 11.9247, and so forth. These numbers are known as real numbers in mathematics, which have strict definitions and rich properties, and are widely used in physical models to depict the positions of time and space. Can we also use real numbers as the foundational mathematical representation in computer science?
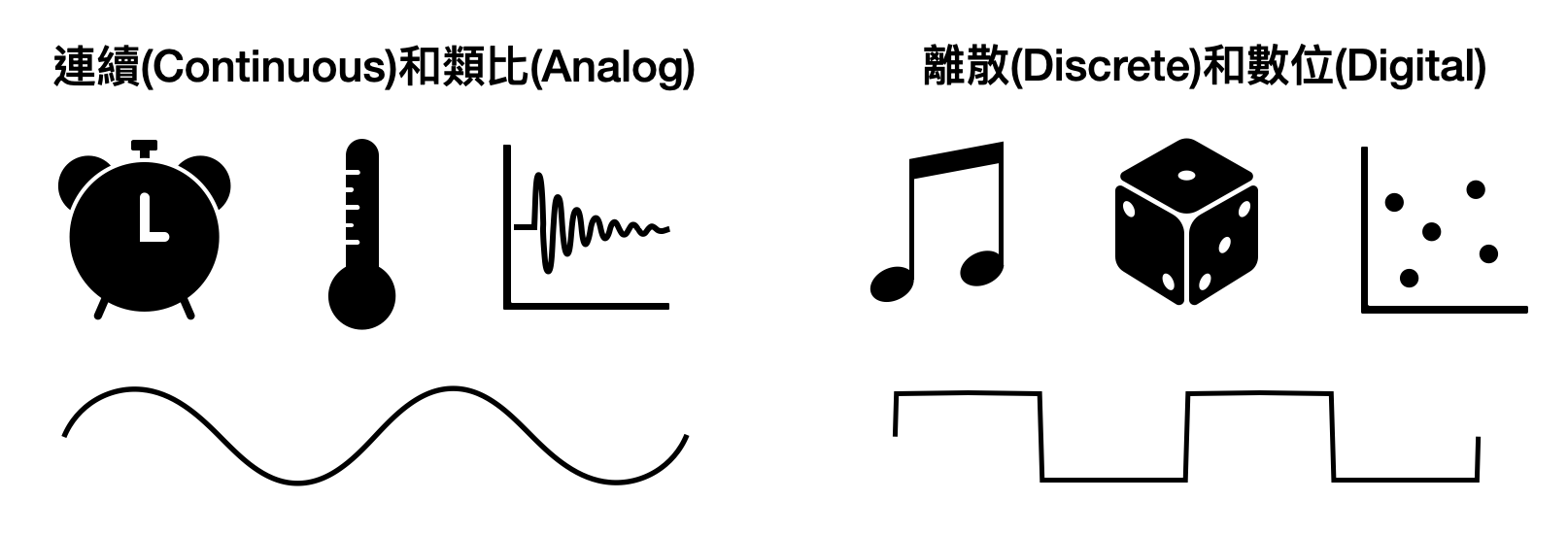
Using real numbers, or more generally, what we call “continuous” mathematical objects, as the foundational language, is referred to as an “analog” signal. The mathematical models in physics are essentially constructed on top of the analog world. Therefore, using analog language to describe computation is a very tempting option, which would allow for a multitude of physical and mathematical tools to be potentially applied.
Another option is the so-called “digital” signal. Unlike analog signals, digital signals use non-continuous, or what we call “discrete,” mathematical objects as the foundational language. For example, integers like 0, 1, 2, 3, etc., are common discrete mathematical objects. The real numbers between 0 and 1, on the other hand, are continuous mathematical objects.
So, should we use analog or digital signals? In terms of results, computer scientists chose digital signals. From a hindsight perspective, on a practical level, digital signals are easier to implement in complex computational combinations and superpositions. Theoretically, digital signals also tend to provide cleaner and clearer analysis and expression in most cases. However, it should be noted that analog and digital signals each have their advantages and disadvantages, and many communication-related fields primarily use analog signals. The use of digital signals by computer scientists might just be a historical coincidence, and perhaps in another parallel universe, we would be using analog signals!
Since we are in a world that uses digital signals, let us set aside the philosophical debate over the merits of both for now and see what the next steps are!
Binary Representation
After choosing to use digital signals to construct the computational world, the next question is: which specific discrete mathematical object should we use as the foundation for everything? Even among discrete mathematical objects, there are a plethora of choices! From the previously mentioned integers to commonly used algebraic structures like groups, rings, fields, or even graphs, these are all viable options rich in mathematical properties. However, sometimes more power does not mean more usability; too many extra mathematical conditions and rules might become stumbling blocks in analysis. Therefore, computer scientists and engineers gradually reached a consensus to use the unstructured 0/1 binary representation as the foundational language of the computational world!
What exactly is binary representation? What does it mean when people say computers use 0s and 1s as their language?
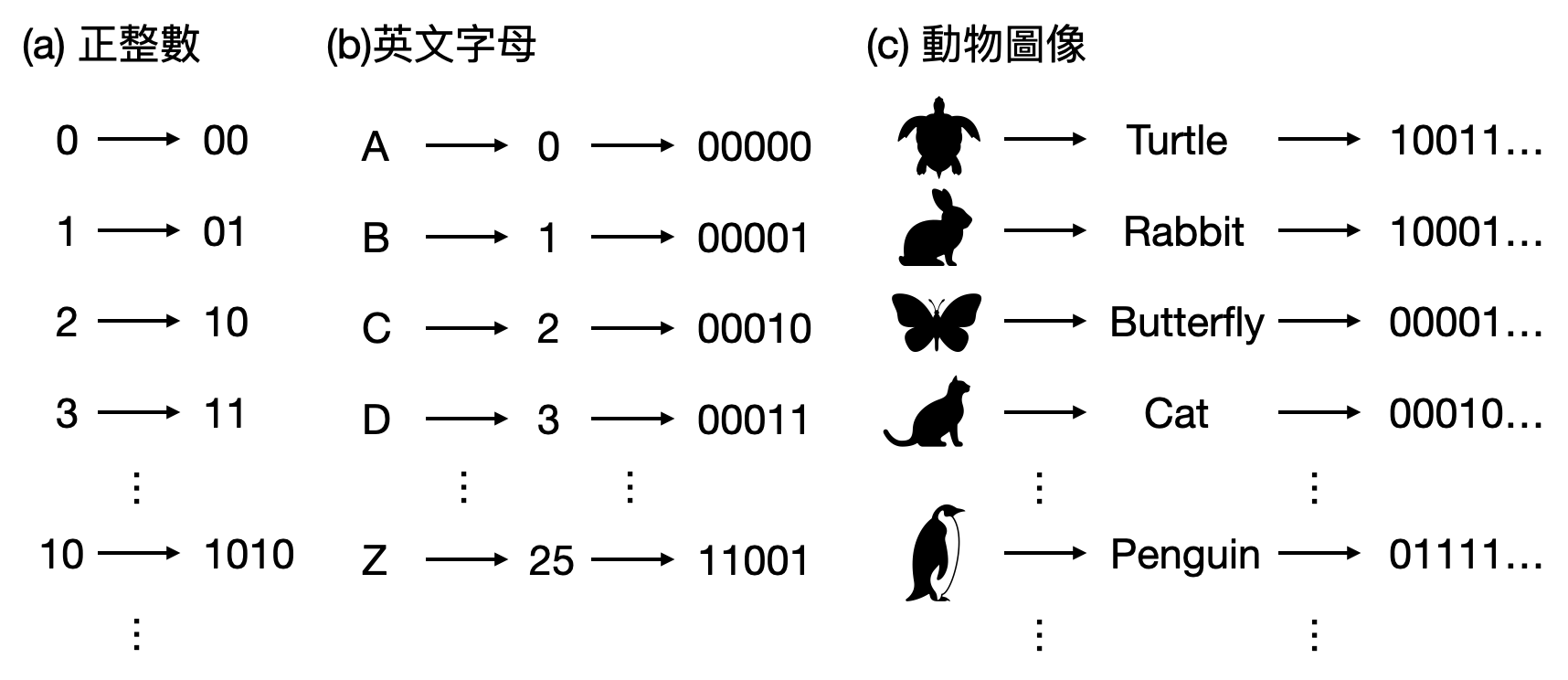
In high school mathematics, some might have learned about the “binary representation” of integers. For example, the number 10 can be represented as 1010, and 99 as 1100011. However, the binary representation mentioned here is not limited to just the binary representation of integers. In fact, all discrete mathematical objects can have a binary representation!
When considering binary representation, besides discussing which specific 0/1 string represents something, a clearer perspective is actually exploring the “encoding” from the objects of interest to 0/1 strings. Encoding, by definition, refers to the rules for labeling objects. For example, during military service, each person is assigned a number based on the lexicographical order of their name in a dictionary. When calling roll, officers use these number encodings instead of the individuals’ actual names. Moreover, we would hope that different individuals receive different encodings, so there are no issues distinguishing between two different people.
Thus, in the artificial world of computation, encodings are usually predetermined based on historical conventions of the field, transforming objects of interest into digital binary representations.
Syntax and Semantics
In any language, there is a variety of symbols (alphabet) and words that combine to form sentences for use and communication. How is a sentence constructed? And how should the meaning of a sentence be interpreted?
These two questions correspond to two important concepts in linguistics: syntax and semantics.
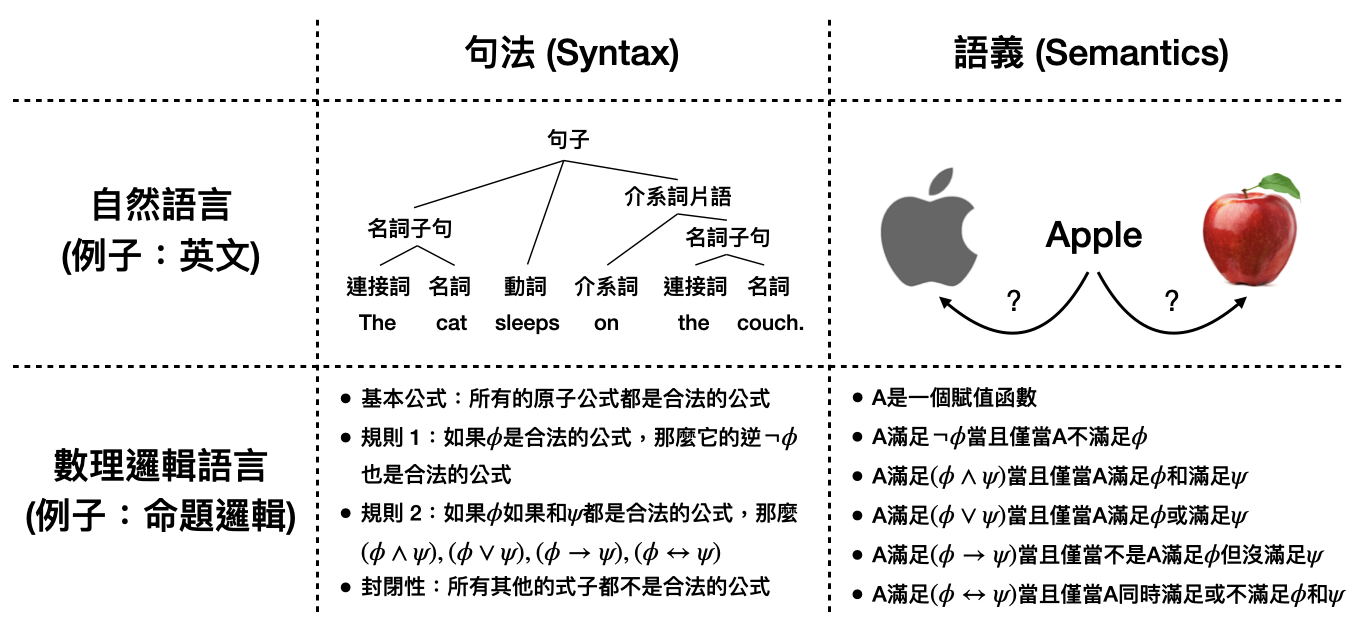
Syntax studies how (reasonable/legal) sentences are formed from combinations of words. For example, when learning English, in addition to vocabulary, we often learn a lot of basic grammar, which tells us the rules for forming acceptable sentences. These rules make up the syntax of the language. In natural languages, common syntactic rules might involve which combinations of parts of speech (such as nouns, verbs, prepositions, etc.) are permissible. Similarly, in mathematical logic languages, syntactic rules are also expressed by defining which combinations of symbols are valid.
Semantics, on the other hand, discusses how to interpret and give meaning to a sentence. Just like when learning vocabulary in English, we learn the possible meanings of each word. Then, we learn what the overall meaning is when these words form a valid sentence. Furthermore, we even learn how different contexts or even different intonations might alter the meaning! In the context of mathematical logic languages, the definition of semantics is often much simpler, generally considering only two meanings: true or false. Specifically, a sentence in mathematical logic, given a particular assignment (or in professional terms, a model), will yield a result of either true or false based on certain rules of interpretation. This result is the semantics of the sentence under that particular assignment/model.
Formal Languages
Syntax and semantics are both deeply intricate and central subfields in the study of language. When we attempt to establish an objective language, it’s inevitable that we must clarify how to mathematically describe syntax and semantics. Now, let’s explore how mathematicians and computer scientists use mathematics to create what’s known as a Formal Language as an objective system of communication.
From our previous discussion, it’s evident that semantics often contains ambiguity in human languages, where the same sentence can be interpreted differently depending on the context or the background of the listener. For instance, when hearing the English word “Apple,” some might first think of a delicious fruit, while others might think of a company that sells electronic devices. In the mathematical world, semantics is easier to handle because a sentence only has two possible interpretations: True or False. This means that in a formal language, any sentence composed of words is either true or false, with no other interpretations.
Since we’ve decided that the semantics of formal languages only include true or false, the choice of syntax becomes straightforward: if a sentence is legal, then we interpret it as true. On the other hand, if a sentence is syntactically illegal, then we interpret it as false. To summarize, when defining a formal language, we first specify some basic symbols (such as the binary symbols 0 and 1), then use some logical mathematical conditions to determine which symbol-composed sentences are legal. Finally, we define the formal language as the set of all legal sentences. For example, in the formal language $L_{palindrome}$ below, a sentence is legal if and only if it is a palindrome (reads the same forward and backward).
\begin{equation*} L_{palindrome} = \{x\in\bit^* \, :\, \forall i=1,\dots,|x|,\ x_i=x_{|x|-i+1} \} \end{equation*} Here, $\forall i=1,\dots,|x|$ means iterating $i$ from $1$ to $|x|$ (i.e., the length of $x$), so the expression after the colon checks if $x$ is a palindrome.
Why do we spend so much effort discussing formal languages? Because theoretical computer scientists use formal languages as models for computational problems! That is, a computational problem in mathematics is essentially a formal language. The “computation” needed is to determine whether a given sentence is a “true” sentence! For instance, the computational problem of “adding two numbers” can be described by the following formal language $L_{addition}$.
\begin{equation*} L_{addition} = \{(x,y,z)\, :\, x+y=z\} \end{equation*} This formal language uses symbols such as the digits 0 to 9 and basic punctuation such as parentheses () and commas , etc.
Different computational problems might use different words; some might use digits and arithmetic symbols, some might use English letters, etc. How can we analyze different computational problems in a unified way?
The simplest way is to represent all words using the same “encoding.” In computer science, the commonly chosen encoding is the binary representation we previously discussed, which means representing all words using 0s and 1s.
The more discerning readers might have noticed that using binary representation, although it unifies the basic words for all computational problems, also creates many words/sentences that did not exist in the original language. However, don’t worry; we just need to define these sentences as illegal/wrong! Now, we are finally ready to use mathematics to define what a computational problem is!
Computational Problem
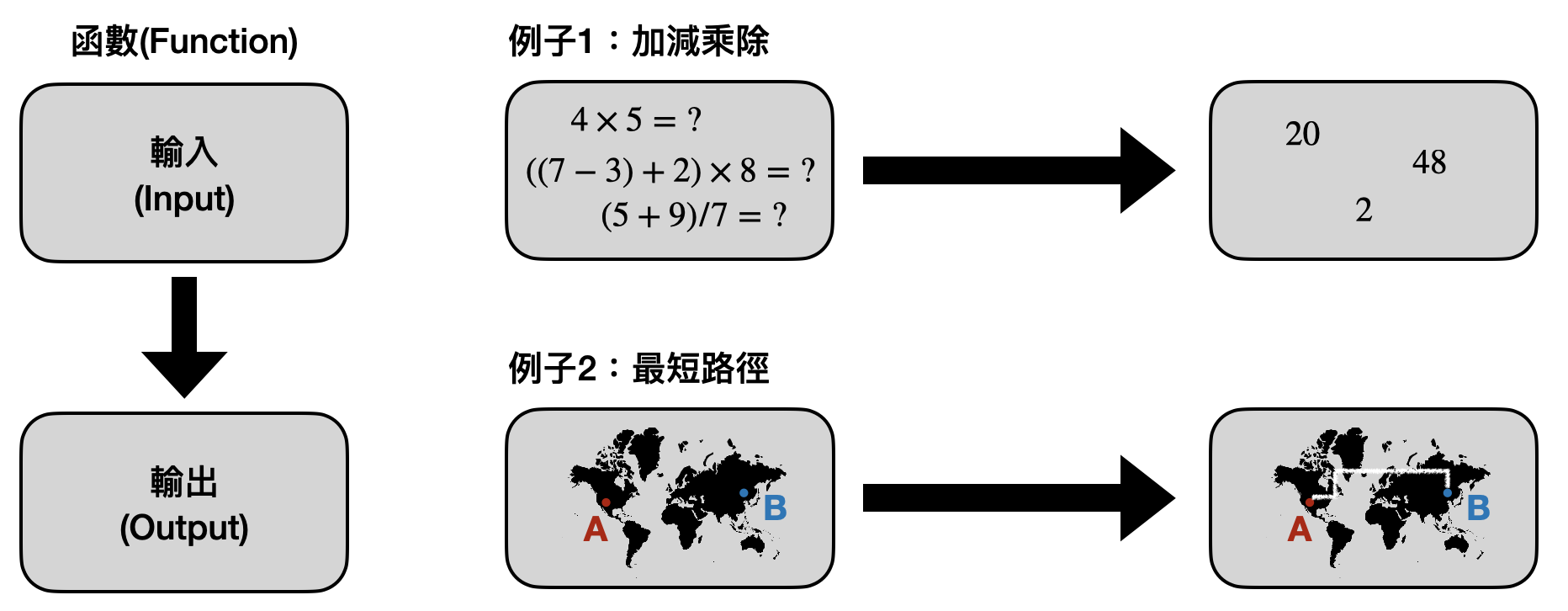
In our everyday lives, computational problems are omnipresent—from solving equations with basic arithmetic during math classes, to mobile apps that find the shortest path between two locations, or even government officials planning how to optimize national operations efficiency. Broadly speaking, a computational problem is essentially a function that maps an input to an output.
However, we quickly notice that the format of inputs and outputs can vary widely for different computational problems. For example, the input for a math problem is various equations, and the output is the solutions. In the case of map navigation, the input is any two points on a map, and the output is a path between these two points. For government decision-making problems, the input could be the entire national situation or even the global economic context, with policy decisions as the output. With such diverse input and output formats, how can we discuss and analyze these problems uniformly?
Human language has already done a fairly good job at this. While reading the above text, despite the inherently different formats of these problems, the descriptions allow readers to form a common understanding of these issues. However, human language often has many ambiguities, which is less than ideal for problem analysis. Additionally, translations between different human languages can potentially lead to misunderstandings. Therefore, before discussing computational problems, we need an objective language that allows everyone to have the same understanding of the same issues.
This is where the binary representation and formal languages we learned about earlier come into play! When discussing a computational problem, we typically start by clarifying the binary representation used for inputs and outputs—that is, how to map paths between two points, solutions to mathematical equations, etc., into strings composed of 0s and 1s. This indeed resolves the issue of having a uniform input and output format for all computational problems. However, if we had to specify the binary representation in detail every time, it would be quite exhausting. Therefore, in practice, there are some “conventional” methods of binary representation that might not use such low-level language in communication but will detail these aspects when implementing on computers.
Previously mentioned formal languages like $L_{palindrme}$ and $L_{addition}$ are computational problems (we could represent the symbols used in $L_{addition}$ in binary so that it is also composed of 0/1 strings). Here’s another example:
\begin{equation*} L_{prime} = \{x\in\bit^* \, :\, x{ is the binary representation of some prime number} \} \, . \end{equation*}
This definition is sometimes referred to as a “decision problem,” which concerns questions of true or false. Often, we might be interested in different scenarios, such as finding a set of solutions to equations or discovering the best strategy. For these situations, theoretical computer scientists also have corresponding mathematical ways to define them.
Different Computational Problems
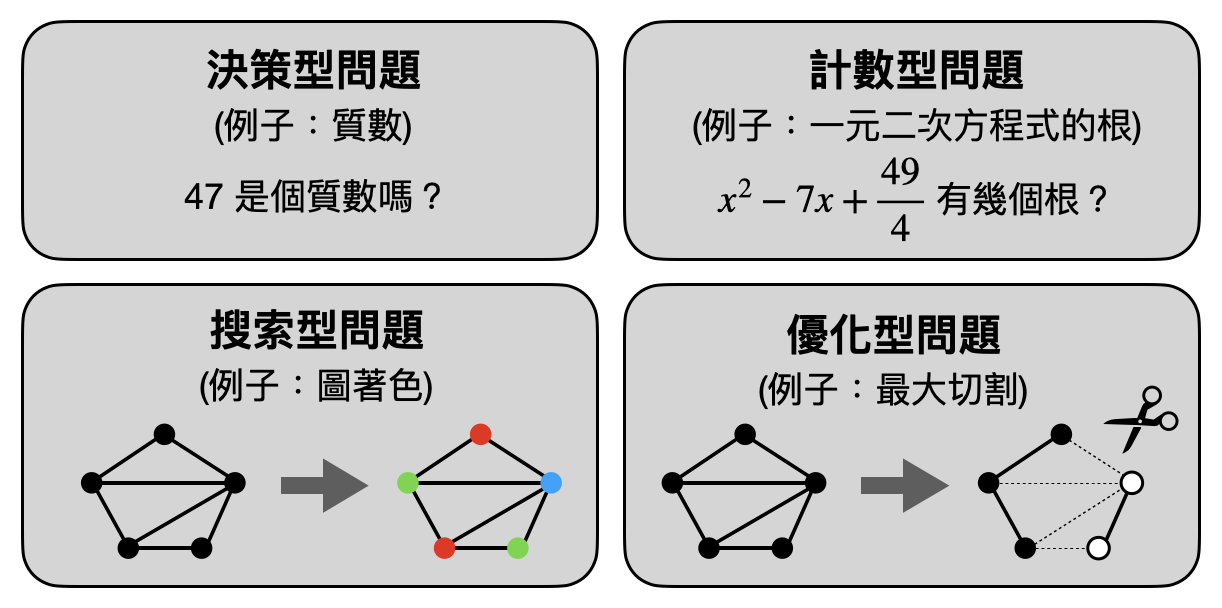
In various application scenarios, we often take an interest in different types of computational problems. Here, we will introduce four common types of computational problems that essentially cover all commonly encountered forms. However, it’s important to note that when we discuss different types of computational problems, we are emphasizing their differences in “input-output formats.” That is to say, for the same issue, we can usually define a version of the computational problem within each of these four types. While these four different versions of computational problems have varying mathematical definitions, fundamentally, they originate from the same issue.
Decision problem This refers to computational problems formatted as "true or false." For example, given a number, the task is to determine whether it is a prime number. Mathematically, this can be described as a function $f:\bit^*\to\bit$ that outputs 0 or 1..
Optimization problem This refers to computational problems that seek "maximum or minimum" answers. For example, given a map and a starting point, the task is to determine the shortest path length between two points. Mathematically, this can be described as a function $f:\bit^*\times\bit^*\to\bbN$ where, where, given the first input $x$ the goal is to compute $\max_yf(x,y)$.
Search problem This refers to computational problems that involve "finding a solution." For example, given a preference ranking table between students and schools, the task is to find a school allocation result such that no two people would want to swap their allocated results. Mathematically, this can be described as a function $f:\bit^*\times\bit^*\to\bit$ where, given the first input $x$, the goal is to find a $y$ such that $f(x,y)=1$.
Counting problem This refers to computational problems that involve "counting occurrences." For example, given a text, the task is to determine how many times a particular word appears. Mathematically, this can be described as a function $f:\bit^*\times\bit^*\to\bit$ where, given the first input $x$, the goal is to count the number of $y$s that satisfy $f(x,y)=1$.
With so many different types of computational problems, must we develop a separate theory for each type, or can we have a unified framework to analyze and study them? An important observation is that all types of computational problems can be described as decision problems! For example, for an optimization problem, if the original task is to find the minimum value of a function $f$, we could add a variable $k$ and ask whether the minimum value of $f$ is less than $k$, thus converting it into a decision problem. Can you think of how to rewrite the other two types of computational problems into the format of a decision problem?
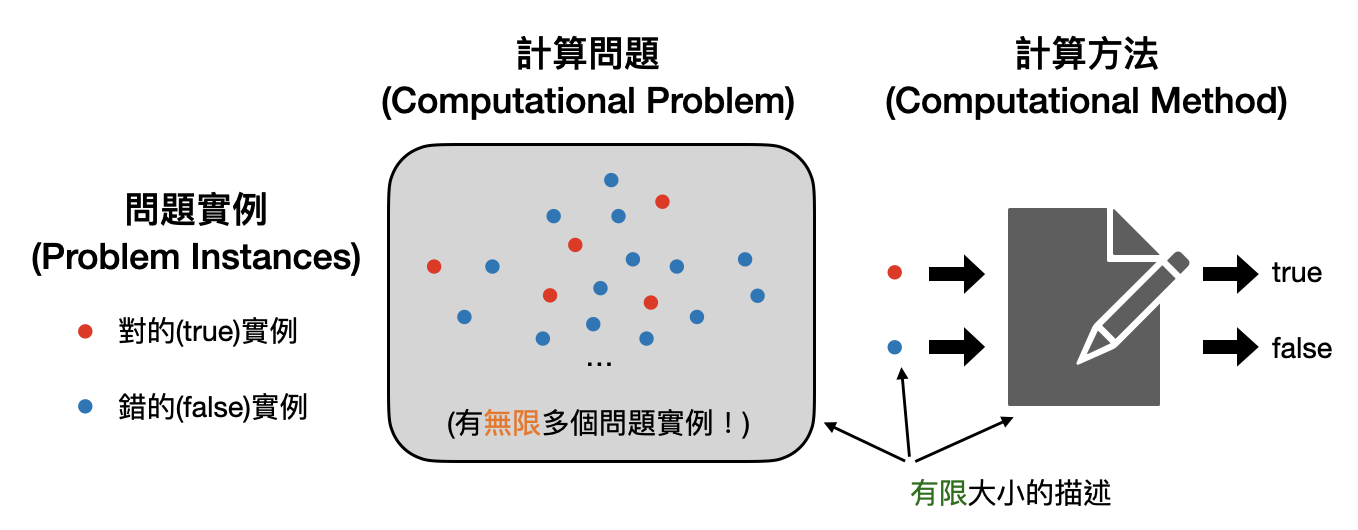
The Difference between Problem and Problem Instance
When we use formal languages as mathematical models for computational problems, it’s important to note that a formal language describes an entire class of problems. For example, the previously mentioned $L_{prime}$ represents the problem of determining whether an input is a prime number. In everyday life, however, we typically encounter specific instances of a problem, such as asking, “Is 28141 a prime number?”
For computer scientists, our concern is with a computational problem, not with a specific problem instance. This means that when we say there is a method to solve the prime number problem, it refers to a method that can tell you whether any given number is a prime. Importantly, before designing this “method,” we do not know which specific instances we will receive. For instance, in solving the quadratic equation $ax^2+bx+c=0$ during a high school math class, we can derive the solution $x=\frac{-a\pm\sqrt{b^2-4ac}}{2}$ without knowing the specific values of $a,b,c$. When faced with an actual problem, such as $5x^2+2x-1=0$, we can calculate $(-(5)\pm\sqrt{2^2-4(5)(-1)})/2$ to find that the solutions are $x=-4,-1$。
In other words, concerning a computational problem, our focus is on how to design a computational method that can guarantee correct outputs for any input.
Computational Methods and Turing Machines
Do you ever wonder about the origins of the everyday terms we hear? Why is it called a computer? Why is it sometimes referred to as a calculator or automaton? What does the term algorithm mean? What are the “machine” and “learning” in “machine learning”?
Let’s use an apparently unrelated example to explain the common origin of these terms. Imagine you are a chef with several sous chefs helping you prepare a big meal. You explain the general steps for each dish to them, then leave the kitchen to chat with the guests. Soon after, a dispute arises between Sous Chef A and Sous Chef B over the first step, “sautéing.” A insists that garlic should be added first to bring out the fragrance with oil, while B argues that garlic burns easily and shouldn’t be added so early. Thus, they both storm up to you, arguing, forcing you to clarify every detail.
This kitchen mishap might occasionally happen in some novice restaurants, but we can imagine that in most establishments, it is impossible for the head chef to explain every step in such detail. Consequently, sous chefs naturally come to understand what specific, finer steps a command entails, even if they encounter a command they have never seen before. Now, let’s conduct a thought experiment: imagine hiring help has become too expensive, and you decide to hire someone with no cooking experience. In this case, you must describe every trivial instruction in detail, from the initial position and angle of the knife to the exact temperature of the oil; you essentially have to write down “all” the steps to ensure nothing goes wrong. For this assistant, each action follows a command without relying on past experience, mechanically executing each directive precisely. Even if you accidentally write the amount of chili ten times too much, they would not discern the error and end up making a mildly spicy dish hellishly hot.
Computers, calculators, automatons, and the like are just like the inexperienced kitchen helper in the example above. They possess strong capabilities to execute any instructions you clearly write, but they will do so exactly as told, even if an oversight on your part leads to the wrong instructions being executed without question.
Hilbert’s Entscheidungsproblem
At this point, a very natural question arises: “Is there a computational method to determine the solution for all computational problems?” This grand question was posed by the great German mathematician David Hilbert (1862-1943) in the last century. This question is sometimes referred to as the “Entscheidungsproblem” or the decision problem.
The challenge with Hilbert’s decision problem isn’t so much in how to answer it, but in how to define this question more precisely. What exactly do the terms “computational method” and “decision” mean in the mathematical context that Hilbert was referring to? In the example of the quadratic equation above, we saw one possible computational approach, which involves expressing the output as a mathematical formula based on the input. But is this the only way to compute?
Let’s consider another example that we’ve encountered before: the prime number problem, $L_{prime}$. Is there a method that, given a positive integer $n$ as input, can tell us whether this number is a prime? This problem doesn’t seem to have a formulaic answer like a quadratic equation. However, in math class, we learned that we could list all integers less than $n$ and greater than 1, and then check to see if any of them divide $n$ without a remainder. If none of these numbers divide $n$, then we know $n$ is a prime. Conversely, if there is any number that divides $n$, then $n$ is not a prime. Here, we see a simple computational method, a way to solve a computational problem without using a formula.
However, such a brute-force approach is very slow, and one might run out of time during an exam without solving many problems. Are there any better and faster computational methods available? How can we use mathematics to characterize all possible computational methods? This is where the father of computer science, Alan Turing (1912-1954), comes into the picture!
Turing Machine
The Turing machine is something all CS students have studied, yet many do not understand its significance. Based on my experience during university, the Turing machine is introduced in the mandatory course “Automata and Formal Languages.” Over half of the students struggle with its intricate definitions and operations, with related homework and exam questions often requiring two to three pages of A4 paper to clearly write the answers. Consequently, many students still do not understand the importance of the Turing machine by the end of the semester.
Therefore, here we will focus on the basic concepts and significance of the Turing machine, while detailed mathematical definitions and examples will be provided in further reading.
The Turing machine is a mathematical model that attempts to describe all feasible computational methods, providing a common foundation for using mathematical analysis to explore the nature of "computation."
Just as Newton’s three laws attempt to describe the mechanical phenomena of the physical world with a few simple mathematical rules, the Turing machine aims to describe any feasible computation method. Specifically, Turing hoped that for any computational method, we could design a corresponding Turing machine and then use this machine to perfectly simulate the original computation process.
So, what exactly is a Turing machine? Let us use the following thought experiment to understand and get to know the ideas behind the Turing machine!
Imagine you are taking a math exam. You have mastered every computational method taught in class, meaning that once you see a question, you can correctly compute the answer by following a certain established process. What would this computation process look like?
First, you read the question and quickly determine the type of problem, such as a linear equation with two variables. You then recall the method for solving such equations and convert the numbers from the question into specific parameters of the equation. Next, you perform a series of operations—addition, subtraction, multiplication, and division—on your scratch paper, and finally compute the answer and fill it in on the answer sheet.
Now comes Turing’s question: How can we describe this “computation process” using mathematical language? One intuitive method might be as follows:
The First Attempt
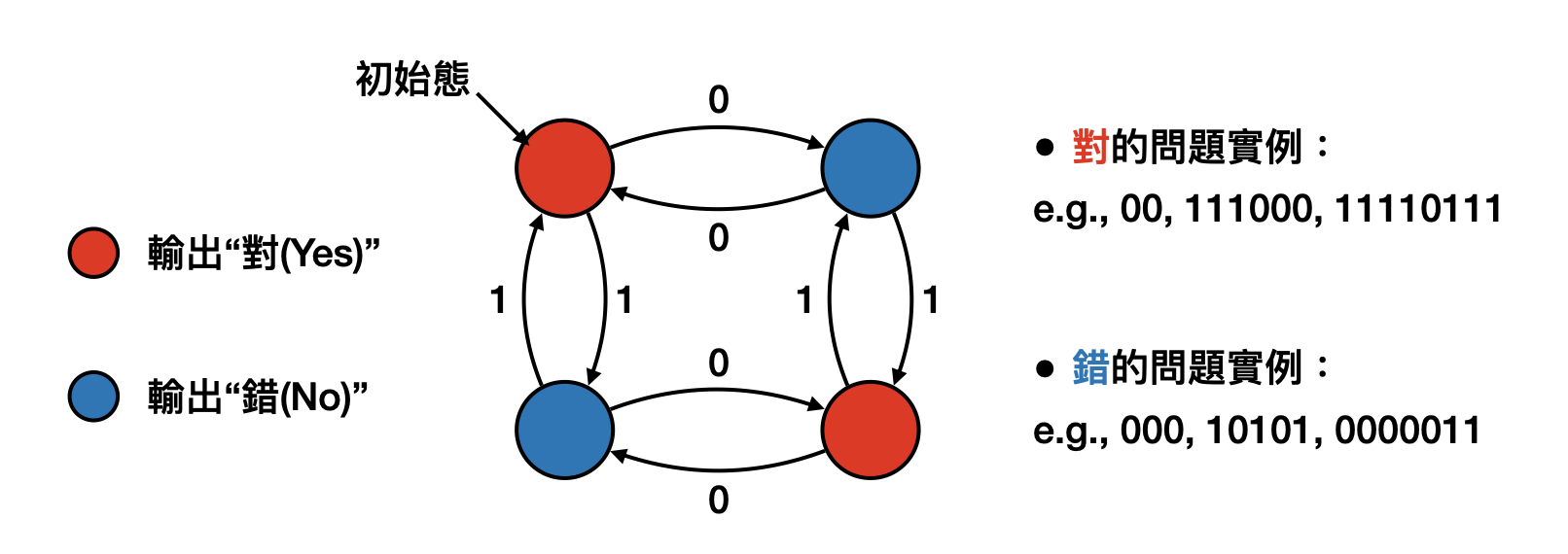
In the computational process described above, we experienced many different “states,” starting from the initial state, transitioning to recognizing the type of problem as solving a system of linear equations, and finally returning to the initial state ready to solve the next problem. This means that the process of computation appears to be a series of “state transitions,” where the rules for transitions are determined based on the input observed and the intermediate results of calculations. If we can clearly describe the states we experience and the relationships between these transitions, it seems that we might be able to fully describe a computational process! This type of computational method is mathematically known as deterministic finite automata (DFA, as shown in the figure below).
Unfortunately, this mathematical model can only describe a very limited range of computational processes. The major problem is closely related to the previously discussed difference between a computational problem and a problem instance:
When designing a computational method, it cannot be tailored to a specific problem instance. This is quite reasonable; otherwise, we could always write the answer to a specific problem instance directly into the computational process. Therefore, in designing a computational method, since we do not know what problem instances will be received as input, the designed states cannot remember an arbitrary amount of information about the input. As such, if we solely use state transitions to describe the computational process, there will be a vast number of seemingly simple computational problems that cannot be addressed with corresponding computational methods. For example, can you design a DFA that computes whether the number of 0s and 1s in an input 0/1 string are equal?
Turing’s Attempt
From the example of the DFA, we have gained a deeper understanding of the challenges in characterizing computational methods. The biggest challenge is how to describe a computational method with a finite mathematical representation without having seen any specific problem instances. Upon reflection, this seems like an impossible task: we are trying to use a finite mathematical model to handle an infinite number of problem instances!
At this point, Turing introduced a key idea to bridge the gap between the finite and the infinite: why not allow the computational space in the mathematical model to expand arbitrarily as needed by the input, while ensuring that the description of the mathematical model remains finitely long. It’s like when we do math; although our brain’s space is limited (corresponding to the finite description of the computation method itself), we essentially have an infinite amount of paper (corresponding to an infinite amount of computational space) to use.
Thus, the Turing machine was born.
To avoid losing the main focus due to mathematical definitions, we will only discuss the conceptual idea of the Turing machine’s definition here.
Let’s take a step back and re-emphasize what exactly a Turing machine is intended to do. Just as physical laws aim to simulate the operational rules of the physical world, Turing also hoped for such a mechanical understanding of computation. The Turing machine provides a robust mathematical model that allows us to intuitively think about computational methods, design corresponding mathematical parameters, and obtain a concrete Turing machine (although still presented in mathematical form). Since a Turing machine is a mathematical object, we can further prove through mathematical discourse that it indeed solves the corresponding computational problem as we desired.
In the end, a Turing machine is essentially a set of mathematical parameters. For readers who are familiar with programming, you can think of these parameters as a set of code. For readers with a background in physics, you can think of these parameters as similar to the parameters in physical equations (e.g., mass, momentum, etc.). The parameters a Turing machine needs include: (1) the states that can be used and a few special states, (2) the symbols that can be used, (3) the transition function. Note that all three types of parameters are of finite size.
Once these parameters are set, the computational method corresponding to a Turing machine works as follows: We start by setting the Turing machine’s state to the initial state and transcribing the input of the computational problem onto paper. Then we continuously decide, based on the current state and what is currently seen on the paper according to the transition function in the parameters, which state to transition to and what to write on the paper. We stop the computation once the Turing machine enters a termination state, and then based on whether the termination state is an accepting state or a rejecting state, we decide whether to output true or false.
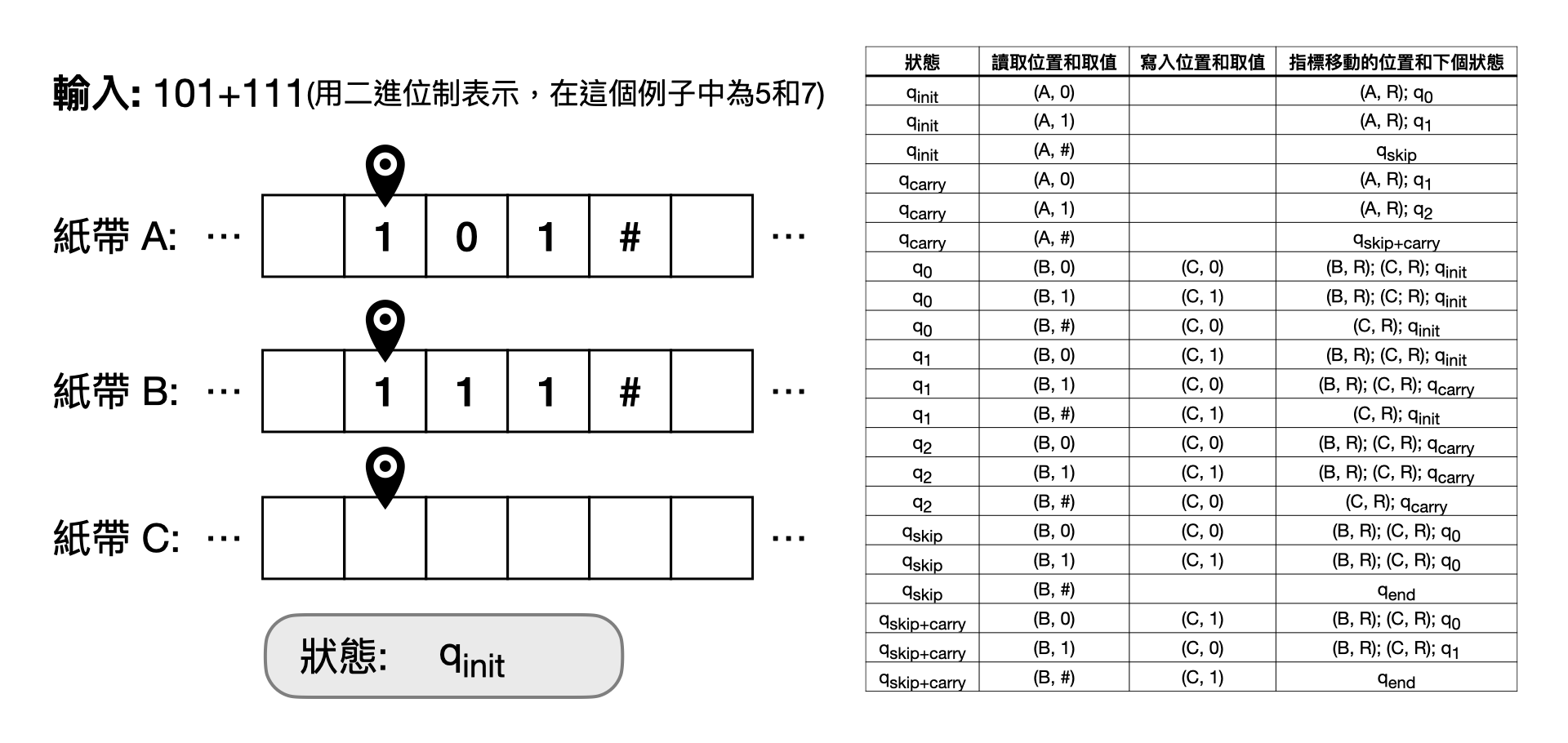
Here is an example of using a Turing machine to perform addition. It’s important to emphasize that when we design a Turing machine, there are usually many ways to select parameters to achieve the same computational function, just as there are different narrative styles and word choices when expressing concepts in writing. So, for readers new to computer science, don’t worry too much about the selection and naming of parameters in the example; just get a general feel for how a Turing machine computes!
一台圖靈機是由三組參數和兩個物件組成的。如上面提到的,三組參數分別為(1)可以使用的狀態以及幾個特殊狀態、(2)可以使用的符號和(3)轉換函數。兩個物件則分別是一條無窮上的紙帶,和一個指針指向紙帶上的一個格子。雖然之前的定義中只有一條紙帶,
但是不難證明具有常數條紙帶(例如10條)是等價於只有一條的,所以在上圖的例子中我們使用了三條讓解釋比較方便。
給定一個計算問題的問題實例後,我們首先將問題的輸入放置在圖靈機的紙帶上,並且將指針對到輸入的第一個位元。接著,我們會執行圖靈機的轉換函數,它會告訴我們三件事情:(i)要不要改變指針指向的格子裡面的符號、(ii)要不要改變圖靈機的狀態和(iii)指針要向左、向右還是不動。如此重複執行圖靈機的轉換函數,直到轉換到了中止的狀態(例如上圖例子中的$q_\text{end}$)。
以上就是圖靈機基本的操作型概念,但想必從未見過圖靈機的讀者一定是還是一頭霧水。在這邊筆者決定只將圖靈機的定義點到為止,是因為不管再多的解釋,都勝不過實際操作一遍。所以感興趣的讀者,歡迎參考本書網頁版的動畫內容,解釋上圖的例子。或是參考延伸閱讀中的教材。
最後,以下是兩個在圖靈機數學定義中的關鍵性質。由於這邊我們把圖靈機嚴謹的數學定義推遲到了附錄,所以這兩個性質可能乍看之下很突兀。不過這兩個性質,或是說更像是兩種“限制”,是Turing能夠證明接下來兩個重要定理的關鍵點。對於有興趣完全理解背後數學的讀者,我推薦先讀一下附錄後再繼續。但對於其他讀者來說,可以試著只要抓到大方向的概念和故事即可。
圖靈機的參數和輸入是不相關的:如同前面一再強調計算問題和問題實例的差別,我們希望一台圖靈機能夠處理的是一個計算問題,而不僅僅是少數幾個問題實例。因此,在設計一台圖靈機的參數時,這組參數是關於整個計算問題,而不會和某個特定的輸入(也就是某個問題實例)有關。這個性質又被稱為一致性(uniformity)。
圖靈機的參數必須是有限的: 圖靈機的參數就像是對應到了一個計算方法的運算規則。如同上面的一些類比,一台圖靈機的參數就好比一個人大腦內的神經元連接方式,或是物理系統的宏觀參數,或一組程式代碼,這些東西全部都是有限大小的!當然,這個限制某種程度上是需要更多深入的哲學討論,不過簡單來說,我們可以試著想想看如果一台圖靈機可以有無限多的參數,那麼他就有可能偷偷把很多問題實例的答案都藏在這些參數裡面了。
The Church-Turing Thesis
Now that we have a more concrete understanding of the Turing machine, and knowing that Turing’s original goal was to ensure that for any computational method, there would be a corresponding Turing machine capable of performing the same calculations, a question arises: What exactly constitutes “any computational method”? This brings us to the bridge between the real world and the mathematical world. Just as all physical theories ultimately provide mathematical models to explain physical phenomena, the Turing machine serves as a model for computational methods that can be realized in the real world. Whether this model is sufficient to describe any computational method is a question that science cannot answer, just as science cannot definitively say whether Einstein’s theory of relativity is the definitive description of the physical universe.
Despite this, scientists and mathematicians still hope to deduce and analyze within the abstract world of mathematics and then return to the real world to see if the conclusions drawn in the mathematical realm are applicable. Since the transition from the real world to the initial basic model in the mathematical world is beyond the scope of science, people can only assume its reasonableness, move forward boldly, and then strengthen confidence in this assumption through ongoing dialogue between theory and experimentation.
For computational methods and Turing machines, the corresponding “assumption” is known as the Church-Turing Thesis.
Church-Turing Thesis: Any computational method that can be feasibly executed in the real world can be simulated by a Turing machine.
Why is the Turing machine a good mathematical definition? Why do computer scientists believe in the Church-Turing Thesis? Why do all students majoring in CS still need to learn about Turing machines in the 21st century?
On a mathematical level, the Turing machine provides a relatively "clean" and easy-to-operate mathematical definition, making many analyses of computational methods intuitive and manageable. When Turing introduced the concept of the Turing machine, his PhD advisor, Alonzo Church, proposed $\lambda$ Calculus as a mathematical model for computational methods. Mathematically, the Turing machine and $\lambda$ Calculus are equivalent; however, since the latter is comparatively complex in terms of analysis and operation, the Turing machine gradually became mainstream and established the foundation of computer science. Nonetheless, $\lambda$ Calculus remains a crucial mathematical model in the domain of mathematical logic, albeit a niche research topic due to the divergence of fields.
On an engineering level, the Turing machine played an iconic role in the early development of computers. This is not to say that engineers directly implement a Turing machine, but rather they use the Turing machine as a benchmark, hoping that the computers they develop can at least match the capabilities of a Turing machine. What does it mean to be just as powerful? Just as we hope a Turing machine can simulate any computational method, if a computer can simulate any Turing machine, then it is as powerful as a Turing machine! Mathematically, if a computational model can simulate any Turing machine, we call it "Turing-complete." In fact, many practical computational models in real life are Turing-complete. This means that we can consider the Turing machine as the "sufficient and necessary condition" for a computational model to be sufficiently powerful.
The Universality Theorem
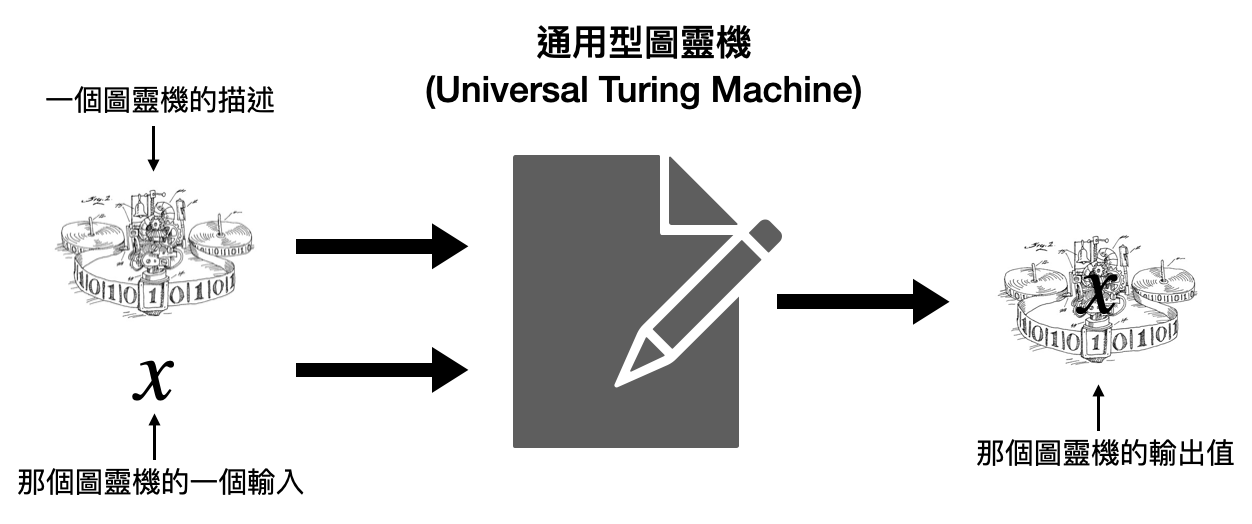
Since we’ve introduced the concept of Turing-completeness, a natural question arises: Can a Turing machine simulate any other Turing machine? Is there a special Turing machine whose input is the parameters and input of another Turing machine, with the goal to accurately simulate that Turing machine’s computation process? This kind of Turing machine is known as a universal Turing machine.
Turing also informed us in his original paper that universal Turing machines do exist! This result has two important implications. First, it tells us that the Turing machine is a very consistent definition mathematically. After all, if we are looking for a mathematical model about computational methods, we naturally hope this mathematical model can capture the computations it can perform. The existence of the universal Turing machine precisely fulfills this requirement. Secondly, a universal Turing machine that can perform “universal computation” allows people to easily write programs and perform various calculations on a single machine. The interpreters in modern computers that let us execute various software codes are essentially acting as universal Turing machines.
The Uncomputability Theorem
So far, we’ve discussed what Turing machines are capable of. However, are there any computational problems that cannot be computed by any Turing machine?
The answer is that almost all computational problems cannot be computed by any Turing machine!
This answer might seem to suggest that the Turing machine might not be a good mathematical model, otherwise, how could it be that most computational problems have no corresponding Turing machine? However, if we recall the definition of a computational problem, a computational problem is a set of 0/1 strings, which essentially never occur in our daily lives! For example, if we define a computational problem as randomly deciding whether a 0/1 string is in a set, then we can analyze that it is highly probable that this computational problem has no corresponding Turing machine. And at the same time, such a random computational problem is not something we would care about in everyday life!
At this point, a more positive conjecture might be that perhaps the computational problems we care about in reality can all be computed by a Turing machine, right? However, Turing discovered that this is not necessarily the case!
This “easily describable” computational problem is the “Halting Problem”. The problem is simple to define: the input is a description of a Turing machine and its input, and the computational goal is to determine whether this Turing machine, upon receiving this input, will eventually stop at some point or will operate endlessly (e.g., in an infinite loop).
The Uncomputability Theorem might seem at first to shatter the foundation of the Church-Turing Thesis. However, this is not actually the case. People have found that, even though we can identify many easily describable computational problems from the Uncomputability Theorem and its extensions that no Turing machine can compute, at the same time, we really cannot think of any other computational method that could solve these problems! That is to say, it appears that these computational problems indeed do not have any method by which they can be solved in the real world.
After this long journey, Turing, with the definition of Turing machines and his faith in the Church-Turing Thesis, officially shattered Hilbert’s hope for the decidability problem: not all computational problems have a method that can determine them. Perhaps Hilbert’s proponents would feel that the Halting Problem is not a natural computational problem, maybe just a special case? After the Uncomputability Theorem was established, mathematicians demonstrated through the “reduction method” mentioned in Chapter 3 of this book that many very natural computational problems still cannot be determined by any Turing machine, such as the famous “Diophantine Problem”.
Summary
In this chapter, we used mathematics, the most abstract language, from the lowest level of digital signals and binary representations to see how simple encoding methods have a rich expressive power. Then, we witnessed how formal languages can eliminate potential semantic contradictions and become the mathematical definition of computational problems. Further, Turing introduced the concept of the Turing machine under the endorsement of the Church-Turing Thesis, and computer scientists believed that all feasible computational methods in the real world can be simulated by a Turing machine. On these foundations, we were finally able to answer the great mathematician Hilbert’s question about decidability. Whether to be happy or sad, Turing’s Uncomputability Theorem told us that even such easily describable computational problems as the Halting Problem cannot have a Turing machine compute them.
In the next chapter, we will see how to explore different computational methods and how different computational resources affect computational capabilities from the remnants of the Uncomputability Theorem.
Extended Readings
Textbooks:
- M. Sipser. Introduction to the Theory of Computation. ACM Sigact News, 1996.
- A. Wigderson. Mathematics and computation: A theory revolutionizing technology and science. Princeton University Press, 2019.
- C. Moore and S. Mertens. The Nature of Computation. Oxford University Press, 2011.
Research papers:
- A. M. Turing. On Computable Numbers, With an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, 1937.
Books, novels, or movies:
- M. Tyldum. The Imitation Game. The Weinstein Company, 2014.