$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



第1章

透過數學來了解計算





If we understand an idea then it is only by mathematically recreating it.

如果我們理解一個想法，那我們一定能夠用數學重新創造它。

Misha Gromov



數學和計算有著密不可分的關係。在中小學的數學課程裡，回家作業中總是充滿了各種“計算題”。對於電腦科學專業的學生來說，各種組合數學、線性代數等等，更是有如家常便飯。不過在這個章節中，我們的重心並不是數學和計算在日常生活中的關係，而是在探討兩者在本質上的連結。簡單來說，我們將要從數學的角度來探索計算的本質。有鑒於不同人對於“數學”有非常不一樣的認知，就讓我們先退一步，釐清一下所謂的“數學思考”到底是什麼意思吧！

數學作為嚴謹抽象的形式化語言

在人類社會中，消息的傳遞、知識的紀錄、人與人之間的溝通，都是建立在各種“語言”之上。無論是中文、英文或是其他的語言，其核心都是一套抽象的符號系統：有著字符(和發音)、語法和語意規則等等。對於懂得兩種以上語言的人來說，應該多少有些下述的經驗：在某些場合可能覺得A語言比較能順暢地表達想法，而在另外的場景卻發現使用B語言更加自然。也就是說，縱使不同的語言都能夠表達心中想說的話，但有些時候，卻感覺某個語言怎麼樣都比其他語言更能夠貼切地傳遞想法。

同樣的，數學也是一種語言。而且在某些情況下，數學可以比其他人類的自然語言更有效且精準地用於表達和溝通。

當來到賭場想要好好的大賺一把時，該如何從牌桌上找到規律並從中找出策略獲利？這時機率論就很自然地浮現了。當想要設計出標新立異的房子，又不希望倒塌的時候，幾何學和三角函數就在轉角處向你揮揮手。

從這些例子中，我們也可以發現，數學作為一種語言的時候，特別擅長於抽象出不同事情和概念背後的相似之處，而且具有非常精細嚴謹的架構。一旦接受了數學世界中幾個基本公理和推理規則之後，每個推導出來的數學定理都是這個抽象世界中的“真理”。當人們時常因為日常語言中，用法和理解的歧異爭論不休時，反觀數學世界中地黑白分明，也難怪無數年輕學子被其深邃之美吸引。

話說回來，希望此時已經說服讀者來用一種“語言的角度”來看待數學，將其看做一個抽象的形式語言，而非只是考試中討人厭的問題。的確在很多時候，為了追求數學中完美的嚴謹性，繁雜的細節容易嚇跑一堆人。然而一個真正好的數學理論，其實會把複雜的事物用更清晰的方式表達出來。在接下來的篇幅裡，我們即將看到前人是如何使用數學這個形式語言，把“計算”這個看似複雜模糊的概念，抽象並且公理化，甚至打開了一個全新的領域：電腦科學。

類比訊號和數位訊號

在建構電腦科學的數學理論架構之前，首先我們需要決定最底層的符號、語言和單位等等。換句話說，該用什麼方式來表示我們想要描述的物件？有什麼樣子的操作/運算是可以做的？以一個百米跑道為例，該如何表示跑者目前所在的位置呢？起點是0，終點是100，三分之一處則是33.3333，而在起跑三秒之後，跑者所在的位置也許是11.9247等等。這些的數字在數學上又被稱為實數(real numbers)，具有著嚴格的定義和豐富的性質，並且被廣泛使用在物理模型中描繪時間和空間的位置。我們是否也能用實數作為電腦科學的底層數學表示呢？

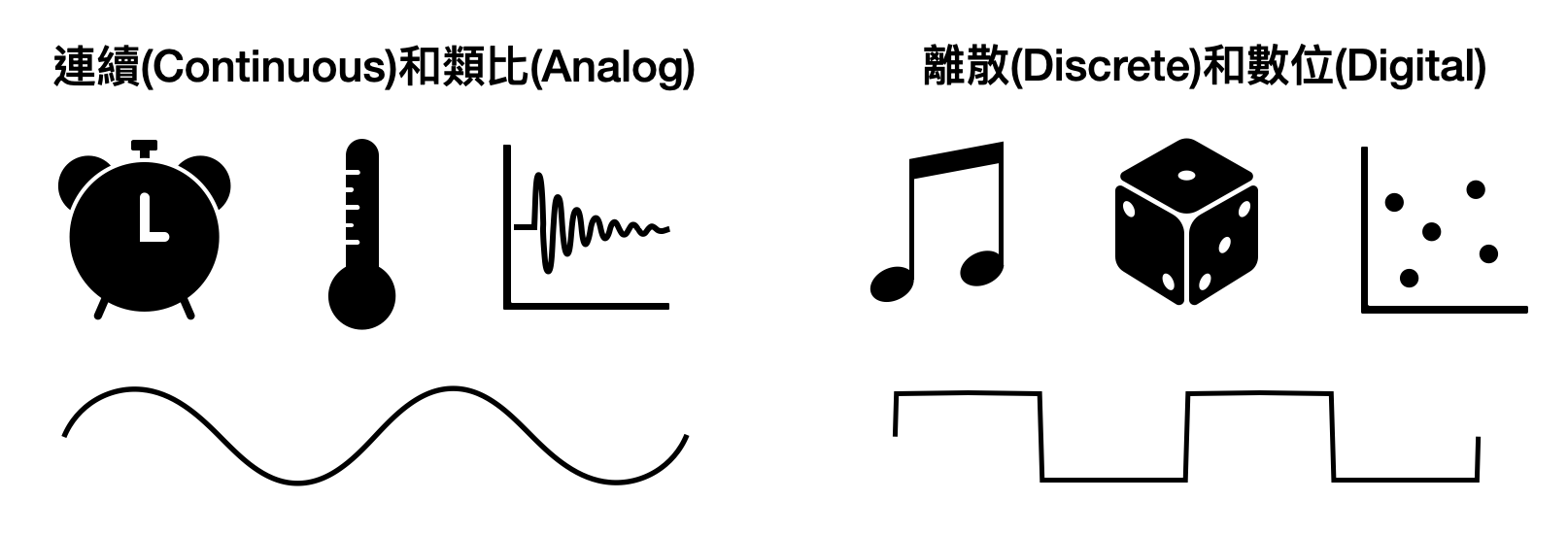
使用實數，或是更廣義來說用所謂「連續(continuous)」的數學物件來作為底層語言，又被稱呼為「類比(analog)」訊號。物理學的中的各種數學模型基本上都是在建構在類比世界之上。因此，用類比語言來描述計算確實是個非常誘人的選項，如此一來，大量的物理和數學工具將會有許多潛在的機會被拿過來應用。

另一個選項則是所謂的「數位(digital)」訊號。和類比訊號相反的是，數位訊號使用了非連續，或是所謂「離散(discrete)」的數學物件來作為底層語言。舉例來說，0,1,2,3等等組成的整數(integer)就是一個常見的離散數學物件。而0到1之間的實數則是連續的數學物件。

連續和類比的例子有時間、溫度等等。離散和數位的例子有音符、骰子的結果等等。

那該使用類比訊號還是數位訊號呢？以結果而論，電腦科學家選擇了數位訊號。從後見之明的角度來看，在實作層面上，數位訊號相較於類比訊號更容易實現複雜的運算組合和疊加。在理論層面上，數位訊號也在大部分的情況有著比較乾淨清晰的分析與表達。不過話說回來，類比訊號和數位訊號各有各的優缺點，許多通訊相關的領域主要使用的是類比訊號。電腦科學家使用數位訊號說不定只是個歷史上的機緣，或許在另一個平行世界我們正使用著類比訊號呢！

不過既然我們身處在使用數位訊號的世界，就讓我們暫且拋去辯論兩者優劣的哲學問題，看看下一步要怎麼做吧！

二元表示

選擇了使用數位訊號來建構計算世界之後，下一個問題就是，我們該使用哪個具體的離散數學物件作為一切的根基呢？就算是離散的數學物件，市面上也有五花八門的選擇！從之前提到的整數，到代數中常用的群(groups)、環(rings)、體(fields)，或是圖(graphs)等等，這些都是具有豐富數學性質的合理選項。然而有時候越強大並不代表越好用，太多額外的數學條件和規則反而可能成為分析的絆腳石。於是電腦科學家和工程師們漸漸地得到了一個共識，使用最沒有結構的0/1二元表示(binary representation)作為計算世界的底層語言！

什麼是二元表示呢？平時大家說電腦使用0和1作為語言到底是什麼意思？

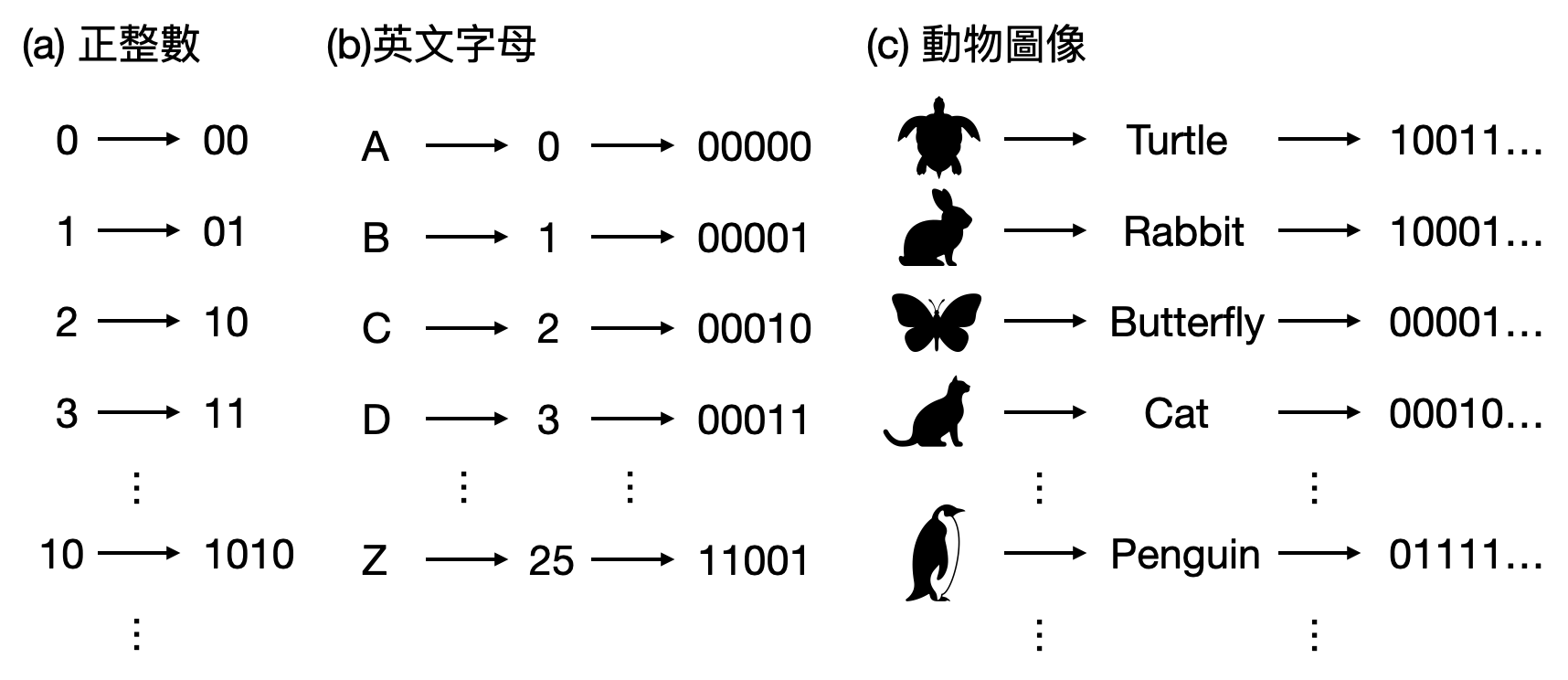
在中學的數學課上，有些人可能曾經學過整數的“二進位表示”。例如10可以被表示為110、99可以被表示為1100011等等。然而上面提到的二元表示，不只侷限於整數的二進位表示。事實上，所有離散的數學物件都可以有個二元表示！

透過先約定好該如何將感興趣的物件編碼至0/1組成的字串。(a)使用正整數的二進位表示來作為其二元表示。(b)將英文字母依序對應到同樣長度的0/1字串作為其二元表示。(c)一旦有了英文字母的二元表示，也可以把其他事物先轉為英文，然後再將每個字母轉為二元表示。

在思考二元表示為何時，除了討論某個東西具體是用哪個0/1字串來表示，更為清晰的觀點其實是探究從感興趣的物件到0/1字串的「編碼(encoding)」為何。顧名思義，編碼指的是將物件貼上標籤的規則。例如在當兵時，每個人會根據姓名字典序的排列，被對應到一串數字。長官在點名時，只會透過這些數字編碼而非每個人原本的名字。同時，我們會希望不同的人拿到的編碼是不一樣的，如此一來才不會有無法分辨兩個不同人的情況發生。

於是，在人造的計算世界中，通常會先依據領域的歷史習慣，約定俗成決定一組編碼，將感興趣的物件轉換成數位的二元表示。

句法和語義

在一個語言中，有著各式各樣的符號(alphabet)和單詞(word)，進而組成了句子(sentence)讓我們可以使用、溝通。一個句子是如何組成的呢？又該如何解讀一個句子的含義？

這兩個問題分別對應到語言學中的兩個重要概念：句法(syntax)和語義(semantics)。

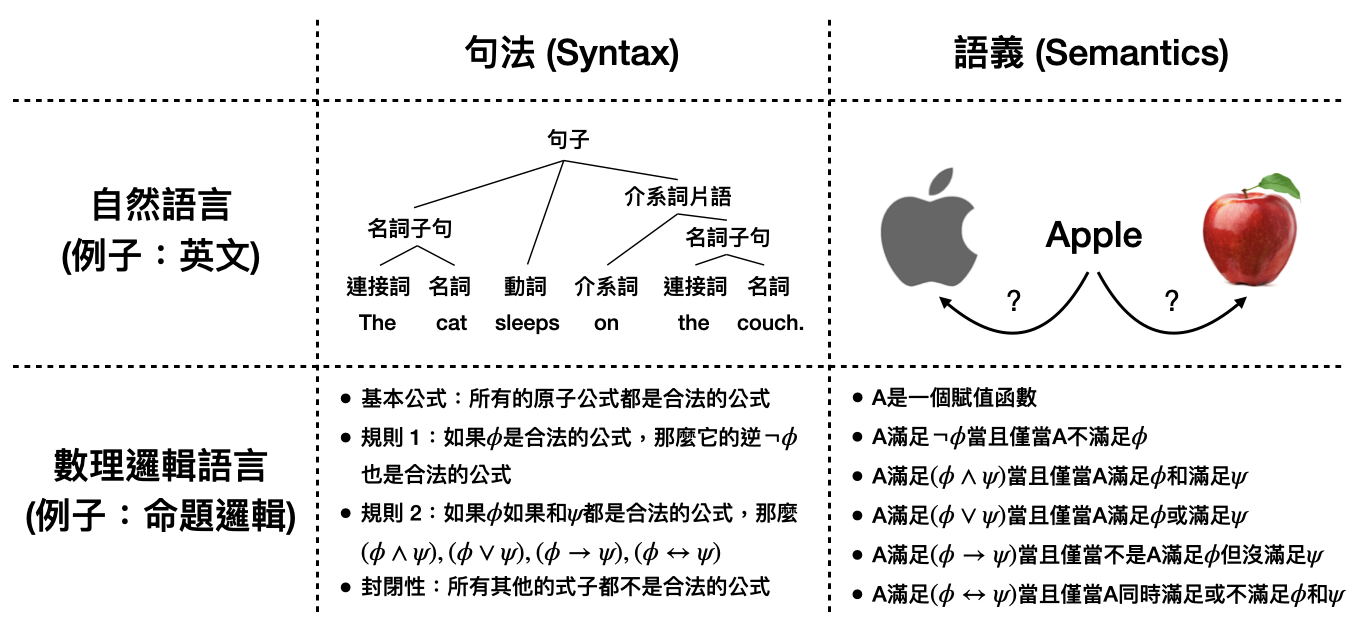
句法是在研究(合理/合法的)句子是如何從單詞的組合中形成，例如我們在學英文的時候通常在單字之外會學一大堆基礎的文法(grammar)，這些告訴我們哪些句子組成方法是合理的規則們，就構成了這個語言的句法。在自然語言中，常見的句法規則會用哪些單字詞性(例如名詞、動詞、介系詞等等)的排列組合是合法的來表示。於是，在數理邏輯語言中，句法規則也是透過定義出哪些符號合併方式是合法的來體現。

語義則是在討論如何解讀和賦予一個句子的意義。就像在背英文單字時，我們會學習每個單字可能具有的含義。接著，我們會學習當單字們組成一個合法的句子之後，所代表的含義是什麼。更進一步，我們甚至要學習在不同的語境之下，甚至不同的語調等等，對應出來的含義到底是什麼！而在數理邏輯語言中，語義的定義通常單純許多，基本上我們只會考慮兩種含義：對(true)或錯(false)。具體來說，一個(數理邏輯)句子，在給定了一個賦值(或專業來說，給定一個模型(model))之後，經由某些規則解讀(interpretation)後，就會得出是對或是錯的結果，作為這個句子在此賦值/模型下的語義。

形式語言

句法學和語義學都是在語言研究中非常核心和深奧的子領域，當我們試圖要建立一套客觀的語言時，無法避免地需要講清楚該如何用數學描述句法和語義。現在我們就要來看看數學家和電腦科學家是如何用數學的方式，建立所謂的「形式語言(Formal Language)」作為一套客觀的語言。

從之前的討論中，我們可以感受到語義在人類語言中時常存在著模糊空間，同樣的句子在不同的情境或是對不同背景的人來說會有很不同的解讀。例如在上圖中，當聽到英文單字“Apple”的時候，可能有些人的第一反應是一種好吃的水果，同時另外有些人的第一反應也許是某個著名的電子產品龍頭。在數學的世界中，語義反而是容易處理的，一個句子只有兩種可能的解讀：對(true)或錯(false)。也就是說，在一個形式語言中，所有單詞組成的句子要嘛是對的，要嘛是錯的，不會有其他的解讀方式。

而既然我們決定形式語言的語義只有對或錯，那麼對於其句法的選擇也就變得很簡單的：只要一個句子是「合法」的，那我們就將它解讀為一個對的句子。反之，如果一個句子在句法上不合法，那我們就將它解讀為錯的句子。總結來說，在定義一個形式語言時，我們首先規定了一些基本的符號(例如二元符號$0$與$1$)，然後用一些數學邏輯條件規定哪些由符號組成的句子是合法的。最後，我們將形式語言定義為所有合法句子組成的集合。例如，在以下的形式語言$L_{回文}$中，一個句子是合法的當且僅當它是一個回文(從前面讀起來和從後面讀回來是一樣的)。

\begin{equation*} L_{回文} = \{x\in\bit^* \, :\, \forall i=1,\dots,|x|,\ x_i=x_{|x|-i+1} \} \end{equation*} 其中$\forall i=1,\dots,|x|$指的是將$i$從$1$到$|x|$(也就是$x$的長度)列舉一遍，所以冒號之後的式子檢查了$x$是否是一個回文。

為什麼我們要花這麼多的篇幅討論形式語言呢？因為，理論電腦科學家就是拿形式語言作為計算問題的模型！也就是說，一個計算問題在數學上就是一個形式語言。而需要做的“計算”就是要來判定一個給定的句子是不是一個“對的”句子！例如，「將兩個數字相加」這個計算問題可以被以下的形式語言$L_{加法}$描述。

\begin{equation*} L_{加法} = \{(x,y,z)\, :\, x+y=z\} \end{equation*} 其中這個形式語言使用的符號為數字0到9以及基本的標點符號例如括號()和逗號,等等。

不同的計算問題可能會使用不同的單詞，有些可能是使用數字和加減乘除符號，有些可能是英文字母等等，這樣該如何有個統一的方式來分析不同的計算問題呢？

最簡單的方式就是把所有的單詞都用同樣的“編碼”來表示！而在電腦科學中，大家一般選用的就是之前我們提到的二元表示，也就是把所有單詞都用0和1來表示。

比較敏銳的讀者可能已經發現了，使用二元表示雖然可以統一所有計算問題的基本單詞，同時也創造了非常多在原本語言中沒有出現的單詞/句子。不過不用擔心，我們只需要把這些句子都定義成是不合法/錯的就好了！現在我們終於準備好用數學來定義什麼是計算問題了！

計算問題

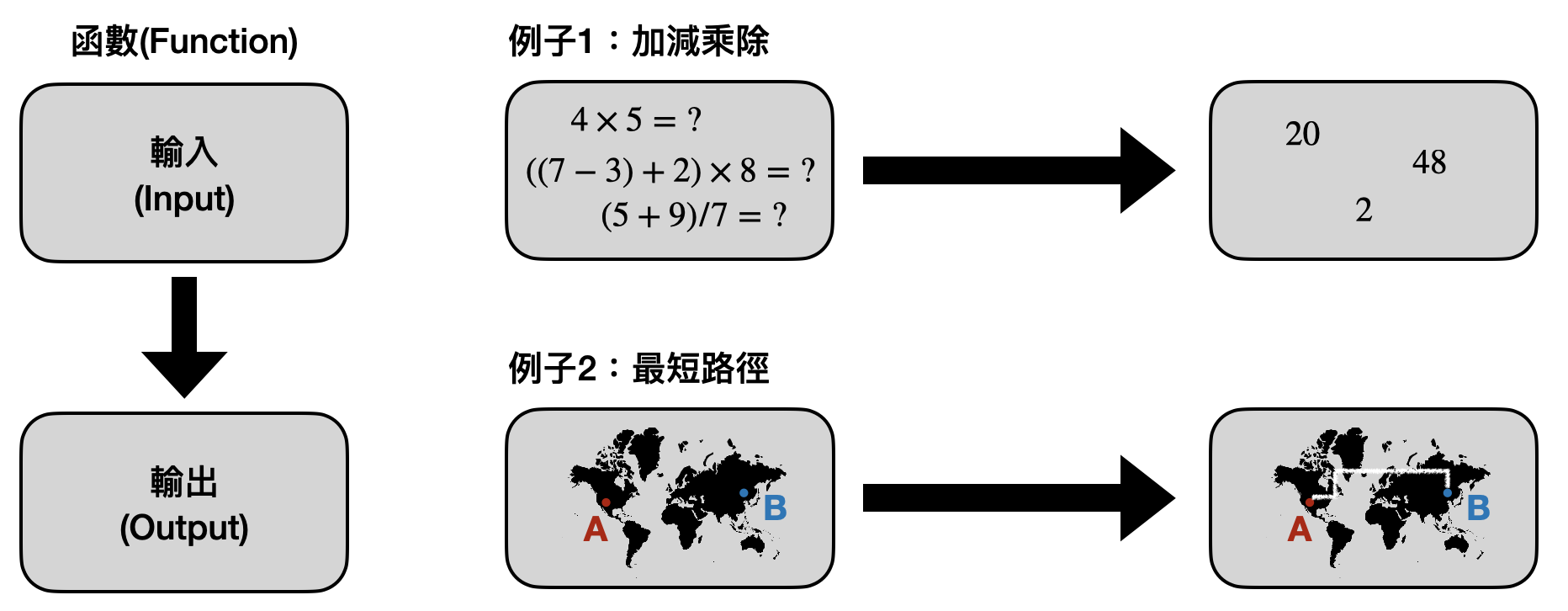
我們的生活中充滿了計算問題(computational problem)，從在數學課上用加減乘除解方程式，到手機中的地圖幫你尋找兩個地點之間的最短路徑，甚至是政府決策人員在規劃如何最佳化國家運作的效率。我們會發現其實最廣義來說，一個計算問題基本上就是個函數(function)，把一個輸入(input)對應到一個輸出(output)。

但這時候我們就會發現，對於不同的計算問題，他們的輸入及輸出的形式(format)可能會不太一樣。以上面的例子來說，數學計算的輸入是各種數學方程式，輸出則是解答。地圖導航的例子中，輸入是任何兩個地圖上的地點，輸出則是兩點之間的一條路徑。對於政府決策問題來說，輸入是整個國家甚至還有全球經濟局勢的狀況，輸出則是政策決定。在這些問題的輸入和輸出形式這麼不同的情況之下，我們該如何進行統一的討論和分析？

其實人類的語言就已經做到不錯的效果了。在你閱讀上一段文字的時候，對於這些不同的計算問題，即使他們本質的形式不太一樣，但是透過文字的描述，讀者們的心中都可以對這些問題有共同的理解。然而我們也知道人類的語言還是常常有許多模糊不清的地帶，這時候對於分析問題來說就不太理想了。而且不同的人類語言之間的轉換等等，更是可能造成潛在的誤會。因此在討論計算問題之前，我們需要一個客觀的語言，能夠讓所有人都對同樣的問題有一樣的理解。

而這時候，前面學到的二元表示和形式語言就派上用場了！當我們在討論一個計算問題的時候，通常會先講清楚輸入和輸出使用的二元表示是什麼，也就是該如何把兩點之間的路徑、數學方程式的解答等等，都對應到0/1組成的字串。雖然這樣的確解決了讓所有計算問題有相同輸入和輸出格式的問題，不過如果每次都要鉅細靡遺地把二元表示寫清楚，大家可能都要累壞了。所以在實際情況中，通常會有些“約定俗成”的二元表示方法，在溝通的時候也許不會使用這麼底層的語言，只有當在電腦實作的時候才會慢慢的把細節刻出來。

一個計算問題是一個0/1字串的集合。等價來說，一個計算問題是一個輸入為0/1字串，輸出為對與錯(0/1)的函數。

在之前章節提到的$L_{回文}$和$L_{加法}$都是一個計算問題(我們可以將$L_{加法}$使用的符號用二元表示使得其也是由0/1字串組成的)，下面是另一個例子。

\begin{equation*} L_{質數} = \{x\in\bit^* \, :\, x{是某個質數的二進位表示} \} \, . \end{equation*}

上述的定義有時候又被稱為「決定型問題(decision problem)」，也就是關於對與錯的問題。而很多時候我們也許在意一些不同的情況，像是要尋找一組方程式的解答，或是找出最佳的策略等等。對於這些情況，理論電腦科學家也有相對應的數學方式來定義。

各種類型的計算問題

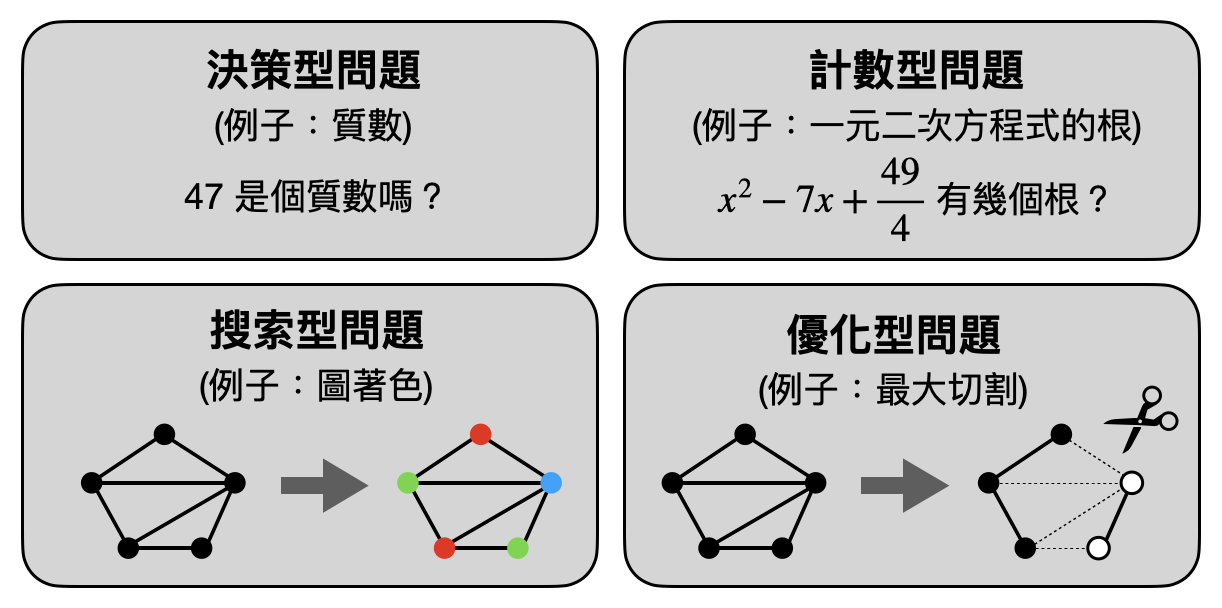
在不同的應用情況下，我們時常會對其他類型的計算問題感興趣。以下我們將介紹四種常見的計算問題類型，基本上包含了所有常見的問題形式。不過在此之前，注意到當我們說不同的計算問題類型時，是在強調它們“輸入輸出形式”的不同。也就是說，對於同樣的問題，我們通常都可以在這四種類型中各自定義一個版本的計算問題。而這四個不同版本的計算問題，雖說數學定義上不太一樣，但是本質上它們是根源於相同的問題。

決策型問題(Decision problem) 指的是形式為「對或錯」的計算問題。例如，給定一個數字，問它是不是質數。數學上可以被描述為一個輸出為0/1的函數$f:\bit^*\to\bit$。

優化型問題(Optimization problem) 指的是在問「最大值」或「最小值」解答的計算問題。例如，給定一張地圖和起始點，問兩點之間最短的路徑長度為何。數學上可以被描述為一個具有兩個輸入的函數$f:\bit^*\times\bit^*\to\bbN$，然後給定第一個輸入$x$，目標是計算$\max_yf(x,y)$。

搜索型問題(Search problem) 指的是「尋找一個解答」的計算問題。例如，給定一張學生和學校之間的喜好排序表，找出一個分發學校的結果使得不會有兩人想要互相交換他們的分發結果。數學上可以被描述為一個具有兩個輸入的函數$f:\bit^*\times\bit^*\to\bit$，然後給定第一個輸入$x$，目標是找出一個$y$使得$f(x,y)=1$。

計數型問題(Counting problem) 指的是「計算個數」的計算問題。例如，給定一篇文章，問某個單字出現了多少次。數學上可以被描述為一個具有兩個輸入的函數$f:\bit^*\times\bit^*\to\bit$，然後給定第一個輸入$x$，目標是計算滿足$f(x,y)=1$的$y$的個數。

這麼多種不同類型的計算問題，難道我們必須針對每個類型都各自建立一套理論，還是可以有個統一的架構來分析研究呢？一個重要的觀察是，其實所有類型的計算問題，都可以被敘述為決策型的問題！例如對於一個優化問題來說，如果本來的問題是要找到某個函數$f$的最小值，我們可以另外增加一個變數$k$，然後改問說$f$的最小值有沒有比$k$還要小，這樣就變成決策型的問題了！你有辦法想到該如何把其他兩種類型的計算問題改寫成決策型問題的形式嗎？

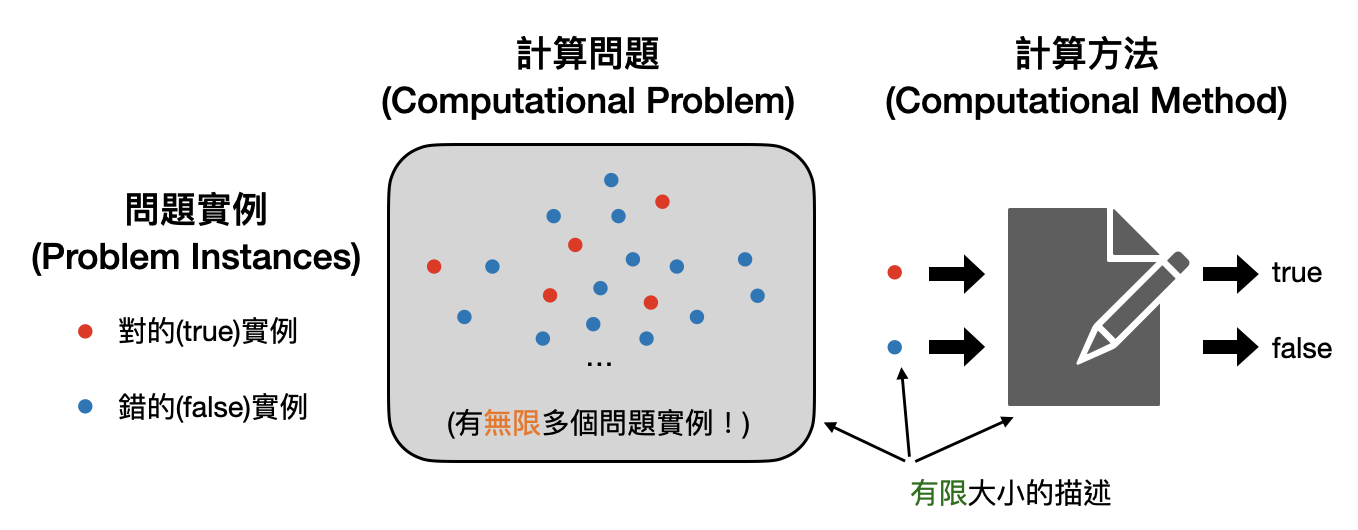
計算問題和問題實例的不同

當我們用形式語言作為計算問題的數學模型時，注意到一個形式語言刻畫的是一整類的問題，例如之前提到的$L_{質數}$，是個判定輸入是否為質數的問題。而平常生活中我們通常遇到的會是一個問題的實例(problem instance)，例如“28141是不是一個質數”？

對於電腦科學家來說，我們在意的是一個計算問題，而非特定的一個問題實例。也就是說，當我們說有個方法可以解決質數問題時，指的是有個方法可以在當你給我任何一個數字時，都告訴你這個數字是不是質數。很重要的是，在設計這個“方法”之前，我們並不知道會拿到哪些具體的實例。就像是在中學數學課解一元二次方程式$ax^2+bx+c=0$的時候，我們可以在不知道$a,b,c$具體是什麼數字的情況之下，推導出答案會是$x=\frac{-a\pm\sqrt{b^2-4ac}}{2}$。當遇到一個實際的問題的時候，例如$5x^2+2x-1=0$，我們可以透過計算$(-(5)\pm\sqrt{2^2-4(5)(-1)})/2$知道答案會是$x=-4,-1$。

也就是說，對於一個計算問題，我們關注的是該如何設計一個計算方法，可以保證對於任何的輸入都正確的輸出解答。

計算方法和圖靈機

不知道大家平時會不會思考日常聽到的各種名詞是怎麼來的？為什麼要叫做電腦？爲什麼有時候又被稱為計算機或自動機？為什麼叫做演算法？“機器學習”中的機器和學習分別是什麼意思？

讓我們用個看似毫不相關的例子來闡述這些名詞由來的共通點。假想你是個廚師，手底下有好幾個副廚幫忙準備一頓大餐。你把所有菜餚的大概步驟跟他們說了一遍，然後就離開廚房去和嘉賓閒聊了。沒過多久，副廚甲就開始和副廚乙對著第一個步驟“爆香”起了爭執，甲認為應該要先下蒜末，這樣才能用油逼出香氣。然而乙卻說大蒜容易焦掉，不應該這麼早就下鍋。於是兩人就氣沖沖的跑到你面前爭論著，讓你不得不把所有細節講清楚。

這個廚房小趣事也許在一些新手餐廳中會偶爾出現，但是我們可以想像在大部分的餐廳中，大廚都不可能如此詳細地把每個步驟說清楚。於是，在幫廚之間自然而然會漸漸知道一個指令會對應到哪些更細微的步驟，即使遇到從沒看過的指令，都還是約略知道該如何實行。現在讓我們再做一個思想實驗，假想現在請幫廚的費用太貴了，你決定請個沒有做菜經驗的人來幫忙。這時候你就不得不把所有的瑣碎指令都詳細描述清楚了，從刀子的起始位子和力道角度，到油溫的確切溫度等等，你基本上必須把”所有“步驟都寫下來，才能確定萬無一失。而對於這個幫手來說，他就是一個指令一個動作，完全不依靠過去的經驗，機械化的把每個指令準確地執行。即使有個地方你不小心把辣椒的分量不小心多寫了十倍，他也無法判別而最終把一道微辣的菜做成了地獄辣。

電腦、計算機、自動機等等，就像是上面例子中這個不會做菜的幫手一樣。它們的能力很強，能夠非常精準的執行任何你寫清楚的指令，但同時它們也就只會完全照做，既使因為你的疏漏下達了錯誤的指令，它們仍然會義無反顧地執行。

Hilbert的可判定性問題

這時候，一個很自然的問題就浮現了：「是不是對於所有的計算問題，都存在一個計算方法判定它呢？」，而恰恰就是上個世紀的偉大德國數學家David Hilbert(1862-1943)提出的大哉問。這個問題有時候又被稱作「Entscheidungsproblem(可判定性問題)」。

Hilbert的可判定性問題其實並不難在該如何回答，而是難在該如何更精確的定義這個疑問。到底Hilbert口中所謂的”計算方法”和“判定”在數學中的定義是什麼？在上面一元二次方程式的例子中，我們看到一種可能的計算方式是把輸出寫成輸入的一個數學公式，然而這是唯一的計算方式嗎？

讓我們來看看另外一個之前出現過的例子：質數問題$L_{質數}$。有什麼方法可以在給定一個正整數$n$作為輸入的時候，告訴我們這個數字是否為質數呢？這個問題似乎沒辦法像一元二次方程式一樣有個公式解答，然而在數學課中我們學到了可以把所有小於$n$和大於$1$的正整數列舉出來，然後算算看是否可以整除$n$。如果所有中間的數字都無法整除$n$，那麼我們就知道$n$是一個質數。反之，如果存在一個中間的數字能夠整除$n$，我們就知道$n$不是質數。在這邊我們看到了一個簡單的計算方法，用公式解以外的方式解決了一個計算問題。

不過這樣暴力的解法實在很慢，可能考試時沒寫幾題就鐘響了，有沒有其他更好更快的計算方法呢？我們該如何用數學來刻劃所有可能的計算方法？這時，電腦科學的祖師爺Alan Turing(1912-1954)出場了！

圖靈機

圖靈機(Turing machine)是個所有CS專業的學生都學過，但是大多不知道為何其重要的東西。在傳統的課綱中(根據筆者當年大學讀書時的經驗)，圖靈機是在大學部必修的「自動機與形式語言」中出現。超過一半的同學深受其繁冗的定義和操作所擾，相關的作業和考試習題動輒就需要兩三頁A4紙把答案寫清楚。也因此，許多人在學期結束後，仍然不知道圖靈機的重要性為何。

所以在這邊，我們將著重在圖靈機的基本概念及意義，詳細的數學定義與例子將會提供在延伸閱讀中。

圖靈機是個數學模型，試圖描述所有可行的計算方法，並且讓人們有共通的基礎來使用數學分析“計算”的本質。

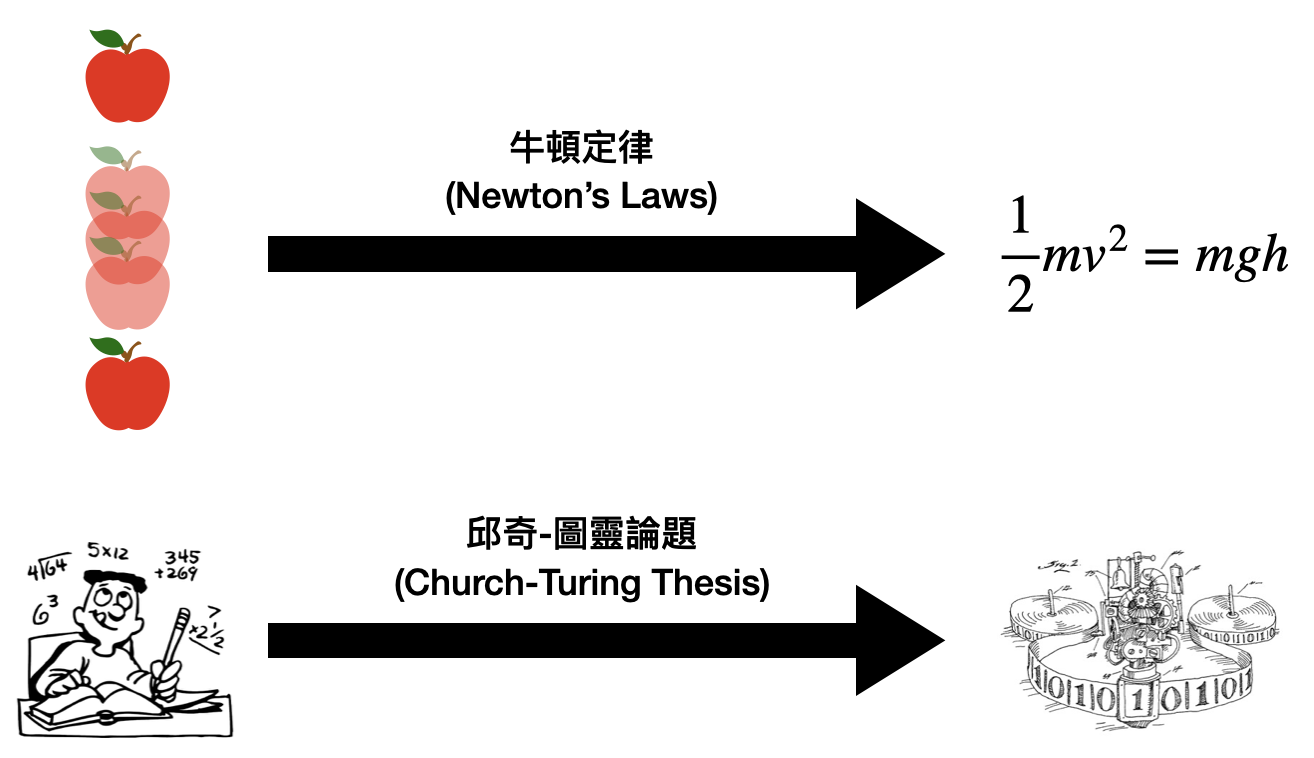
就像牛頓三大定律試圖用幾個簡單的數學規則來描述物理世界中的力學現象，圖靈機想要描述的則是任何可行的計算方法。確切來說，圖靈希望對於任何的計算方法，我們都可以設計出相對應的一台圖靈機，然後用這台圖靈機完美的模擬原本計算方法的計算過程。

那麼圖靈機到底是什麼呢？就讓我們用以下的小小思想實驗，來理解和認識圖靈機背後的思想吧！

想像你正在參加一個數學考試，你已經對於上課所學過的每個計算方法瞭若指掌，也就是說，一旦看到了題目，只要照著某個既定的流程，你就一定能正確地把答案算出來。這會是個什麼樣計算過程呢？

首先，你閱讀了一下題目，然後迅速判斷題型是什麼。例如，是個解二元一次方程式的題目。於是你回想了一下二元一次方程式的解題方法是什麼，並且把題目中相對應的數字轉換成方程式的具體參數。接著，你在計算紙上照著公式做了一系列的加減乘除，最終把答案算出來並填入答案紙。

那麼Turing的問題來了，我們該如何用數學的語言，來描述上面這個”計算過程”呢？一個很直覺的方法可能是如下：

第一個嘗試

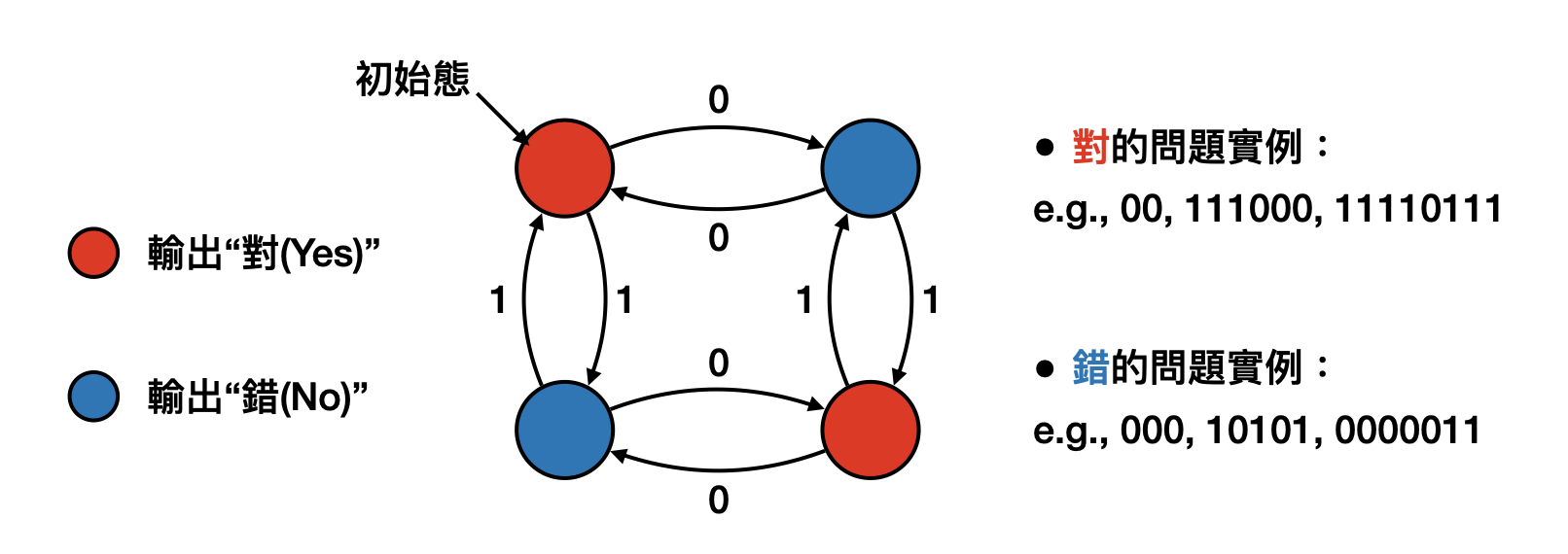
在上面的計算過程中，我們經歷了許多不同的“狀態(state)”，從初始狀態，到看了題目後判斷是什麼問題轉換到解二元一次方程式的狀態，到最後計算完成回到了初始狀態準備解下一題。也就是說，計算的過程看起來就像是一連串“狀態轉換(state transition)”的過程，而轉換的規則是根據看到的輸入以及中間的計算結果是什麼來決定。只要把會經歷到的狀態以及這些狀態之間的轉換關係描述清楚，我們似乎就可以完整地描述一個計算過程了！？上述的這種計算方法，在數學上又被稱為確定有限狀態自動機(deterministic finite automata, DFA, 如下圖)。

考慮以下的計算問題：當輸入的0/1字串中，0的個數和1的個數的奇偶性一樣時，就是對的輸入。如果不同，則是錯的輸入。這個DFA運作的方法如下：從左上角的初始態開始，然後從頭到尾讀輸入的0/1字串，並且依照看到的0或是1，依照箭頭上的0和1來轉換不同的狀態。最終，根據最後停留的狀態來決定要輸出對或錯。

很可惜的，這樣的數學模型能夠描述的計算過程是非常有限的。而最大的癥結點，和之前討論到計算問題和問題實例的差別密切相關：

在設計一個計算方法的時候，並不能夠針對某個問題實例。其實這也非常的合理，要不然我們總是能把某個問題實例的答案直接寫在計算過程中就好了。於是，在設計一個計算方法時，因為不知道會拿到什麼問題實例作為輸入，所以設計的狀態中並不能記住任意多關於輸入的訊息。如此一來，如果我們純粹只用狀態之間轉換來描述計算過程，就會有非常大量看似簡單的計算問題，卻沒辦法有相對應的計算方法。舉例來說，你有辦法設計出一個DFA來計算輸入的0/1字串中，0和1的個數是否相同嗎？

一個計算問題、一個問題實例、和一個計算方法，都是「有限大小」的。一個計算問題中，擁有「無限多的問題實例」，而計算方法需要能夠處理任意的問題實例！

Turing的嘗試

從DFA的例子中，我們對於刻畫計算方法的困難度有了更多的了解，最大的挑戰尤其是該如何在沒有看到具體問題實例的情況下，仍然用有限的數學描述來刻畫一個計算方法。仔細想想的話，會發現這看似是一個不可能做到的事情：我們想用有限大小的數學模型，來處理無限多的問題實例！

這時，Turing提出了一個關鍵的想法來處理這個有限與無限之間的鴻溝：要不我們讓數學模型中的計算空間可以隨著輸入的需要任意增加，但同時我們確保這個數學模型的描述仍然是有限長的。就像我們在算數學時，雖然我們大腦的空間有限(對應到計算方法本身的數學描述是有限的)，但是基本上我們有無限多的紙(對應到有無限多的計算空間)可以使用。

於是，圖靈機就這樣誕生了。

為了避免讀者因為數學定義迷失了大方向，在這邊我們將只會討論圖靈機定義的圖像概念。

先讓我們小小退後一步，再強調一次圖靈機到底是想要來做些什麼？如同物理定律想要模擬物理世界的運行規則，Turing也希望對於計算能夠有如此機械性的理解。圖靈機提供了一個足夠強大的數學模型，讓我們可以很直覺的思考計算方法，並且設計相對應的數學參數並得到一台具體的(雖然仍然是以數學的形式呈現)圖靈機。由於圖靈機是個數學物件，我們進一步可以透過數學的論述，證明它真的會照著我們希望的方式解決了相對應的計算問題。

說到底，一台圖靈機其實就是一組數學參數。對於會寫程式的讀者來說，可以把這組參數想成像是一組代碼。對於物理背景的讀者來說，可以把這組參數想成像是一組物理方程式中的參數(e.g., 質量、動量等等)。而一台圖靈機所需要的參數包含了：(1)可以使用的狀態以及幾個特殊狀態、(2)可以使用的符號、(3)轉換函數(transition function)。注意到，這三種參數都是有限大小的。

當設定好這些參數之後，一台圖靈機對應到的計算方法則是如下：首先我們會將圖靈機的狀態設定在初始態，並且把計算問題的輸入抄寫在紙上。接著我們不斷地根據參數中的轉換函數，根據當下的狀態和紙上目前看到的內容，來決定要轉換到哪個狀態以及要在紙上寫下什麼。一直到圖靈機進入了終止狀態，我們就會停止計算，然後根據終止狀態為接收態(accepting state)或是拒絕態(rejecting state)來決定要輸出對或錯。

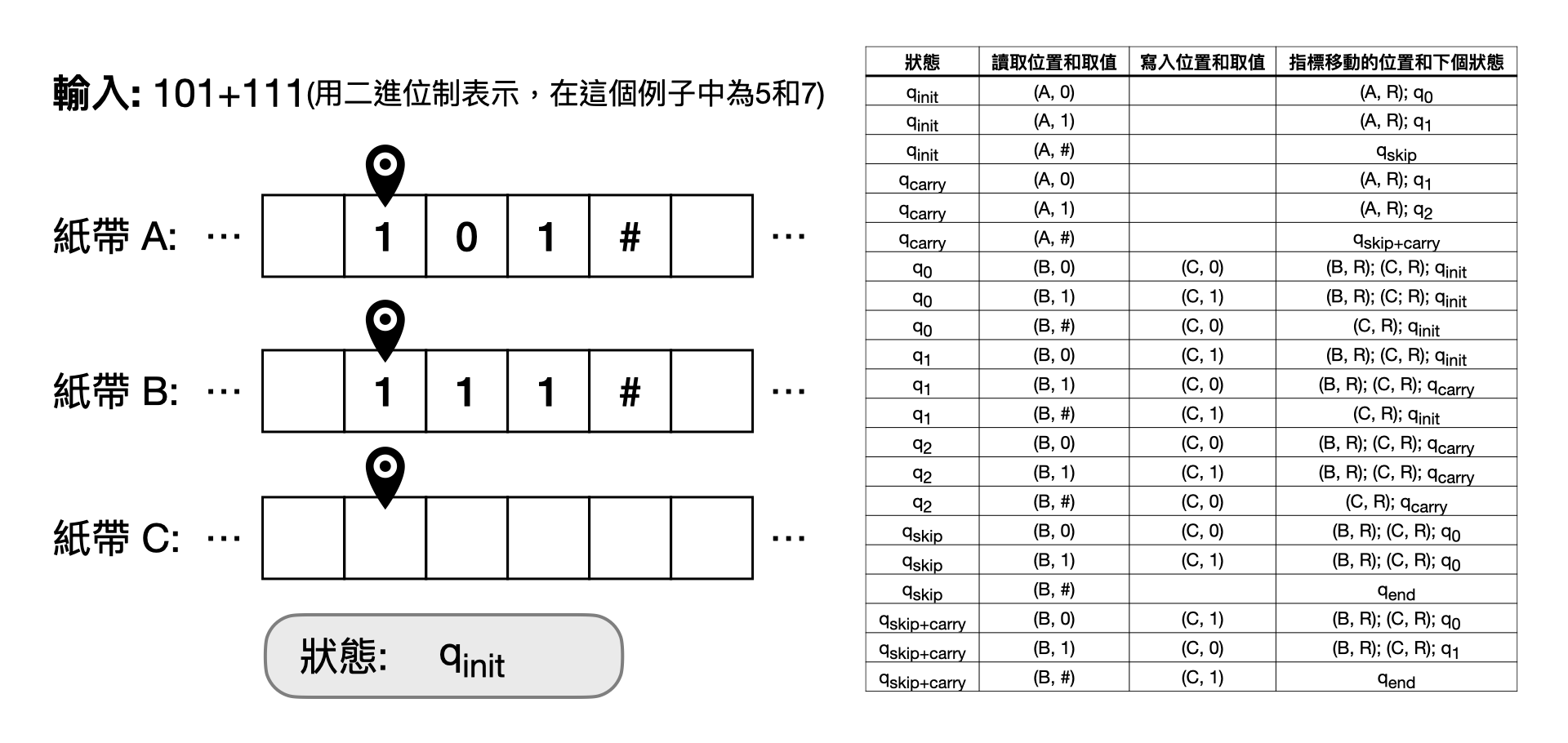
以下是個使用圖靈機做加法的例子。在這邊要特別強調一個概念，當我們在設計圖靈機的時候，通常會有非常多選取參數的方式可以實現相同的計算功能。就如同在寫文章表達概念的時候，每個人可能會有不同的敘事方法和用字遣詞。所以對於剛接觸電腦科學的讀者，可以不要太受到例子中參數的選擇和命名所苦惱，只要大概感受一下圖靈機是如何做計算的就好了！

一台圖靈機是由三組參數和兩個物件組成的。如上面提到的，三組參數分別為(1)可以使用的狀態以及幾個特殊狀態、(2)可以使用的符號和(3)轉換函數。兩個物件則分別是一條無窮上的紙帶，和一個指針指向紙帶上的一個格子。雖然之前的定義中只有一條紙帶，

但是不難證明具有常數條紙帶(例如10條)是等價於只有一條的，所以在上圖的例子中我們使用了三條讓解釋比較方便。

給定一個計算問題的問題實例後，我們首先將問題的輸入放置在圖靈機的紙帶上，並且將指針對到輸入的第一個位元。接著，我們會執行圖靈機的轉換函數，它會告訴我們三件事情：(i)要不要改變指針指向的格子裡面的符號、(ii)要不要改變圖靈機的狀態和(iii)指針要向左、向右還是不動。如此重複執行圖靈機的轉換函數，直到轉換到了中止的狀態(例如上圖例子中的$q_\text{end}$)。

以上就是圖靈機基本的操作型概念，但想必從未見過圖靈機的讀者一定是還是一頭霧水。在這邊筆者決定只將圖靈機的定義點到為止，是因為不管再多的解釋，都勝不過實際操作一遍。所以感興趣的讀者，歡迎參考本書網頁版的動畫內容，解釋上圖的例子。或是參考延伸閱讀中的教材。

最後，以下是兩個在圖靈機數學定義中的關鍵性質。由於這邊我們把圖靈機嚴謹的數學定義推遲到了附錄，所以這兩個性質可能乍看之下很突兀。不過這兩個性質，或是說更像是兩種“限制”，是Turing能夠證明接下來兩個重要定理的關鍵點。對於有興趣完全理解背後數學的讀者，我推薦先讀一下附錄後再繼續。但對於其他讀者來說，可以試著只要抓到大方向的概念和故事即可。

圖靈機的參數和輸入是不相關的：如同前面一再強調計算問題和問題實例的差別，我們希望一台圖靈機能夠處理的是一個計算問題，而不僅僅是少數幾個問題實例。因此，在設計一台圖靈機的參數時，這組參數是關於整個計算問題，而不會和某個特定的輸入(也就是某個問題實例)有關。這個性質又被稱為一致性(uniformity)。

圖靈機的參數必須是有限的： 圖靈機的參數就像是對應到了一個計算方法的運算規則。如同上面的一些類比，一台圖靈機的參數就好比一個人大腦內的神經元連接方式，或是物理系統的宏觀參數，或一組程式代碼，這些東西全部都是有限大小的！當然，這個限制某種程度上是需要更多深入的哲學討論，不過簡單來說，我們可以試著想想看如果一台圖靈機可以有無限多的參數，那麼他就有可能偷偷把很多問題實例的答案都藏在這些參數裡面了。

Church-Turing論題

現在我們對於圖靈機有比較具體一點的概念了，也知道Turing當初的目標是希望對於任何的計算方法，都可以有一台相對應的圖靈機進行一樣的計算。然而什麼是“任何的計算方法”呢？這就牽扯到了現實世界和數學世界之間的橋樑了。如同一切的物理理論終究是解釋物理現象的數學模型，圖靈機是個對於現實中可以實現的計算方法的模型。至於這樣的模型足不足夠描述任何的計算方法，這是個科學無法回答的問題，就像科學也無法告訴你愛因斯坦的相對論是不是就是物理世界的運行方式一樣。

儘管如此，科學家和數學家仍然希望能夠在抽象的數學世界裡面進行推演和分析，然後再回來現實世界看看數學世界中得到的結論是否相關。由於從現實世界到數學世界中最初的基本模型是個超出科學範疇的問題，人們只能透過假設其合理性，昂首向前行，然後透過往後理論和實驗間的對話來加強對於這個假設的信心。

而對於計算方法和圖靈機來說，相對應的這個“假設”則被大家稱為Church-Turing論題(Church-Turing Thesis)。

Church-Turing論題：所有現實世界中可行的計算方法，都可以被一台圖靈機模擬。

為什麼圖靈機是一個好的數學定義？為什麼計算機科學家相信Church-Turing論題？為什麼在二十一世紀所有主修CS的學生還需要學圖靈機？

在數學層面上，圖靈機提供了一個相對"乾淨"好操作的數學定義，使得許多關於計算方法的分析變得直覺又好處理。其實在Turing提出圖靈機的概念時，他的博士指導教授Alonzo Church提出了$\lambda$ Calculus作為計算方法的數學模型。在數學上圖靈機和$\lambda$ Calculus是等價的，然而由於後者在分析操作上比前者相對複雜，於是圖靈機漸漸成為主流，並且成為電腦科學的根基。不過其實在數理邏輯的領域，$\lambda$ Calculus仍然是個非常重要的數學模型，只不過因為領域的分化而成為了小眾的研究課題。

在工程層面上，圖靈機在電腦發展的初期扮演了一個指標性的存在。這並不是說在工程中人們會直接實現一台圖靈機，而是說大家會以圖靈機作為一個基準，希望實現的電腦至少要能夠和圖靈機一樣厲害。一樣厲害是什麼意思呢？如同我們希望圖靈機能夠模擬任何的計算方法一樣，如果電腦也能夠模擬任何的圖靈機，那不就是和圖靈機一樣厲害了！在數學上，如果一個計算模型能夠模擬任何的圖靈機，那麼我們就會稱之為「圖靈完備的(Turing-complete)」。其實在現實生活中，有非常多實際的計算模型都是圖靈完備的。也就是說，我們可以把圖靈機想成是一個計算模型要能夠足夠厲害的“充分必要條件”。

Church-Turing論題之於計算理論，就像牛頓定律之於牛頓力學

通用性定理

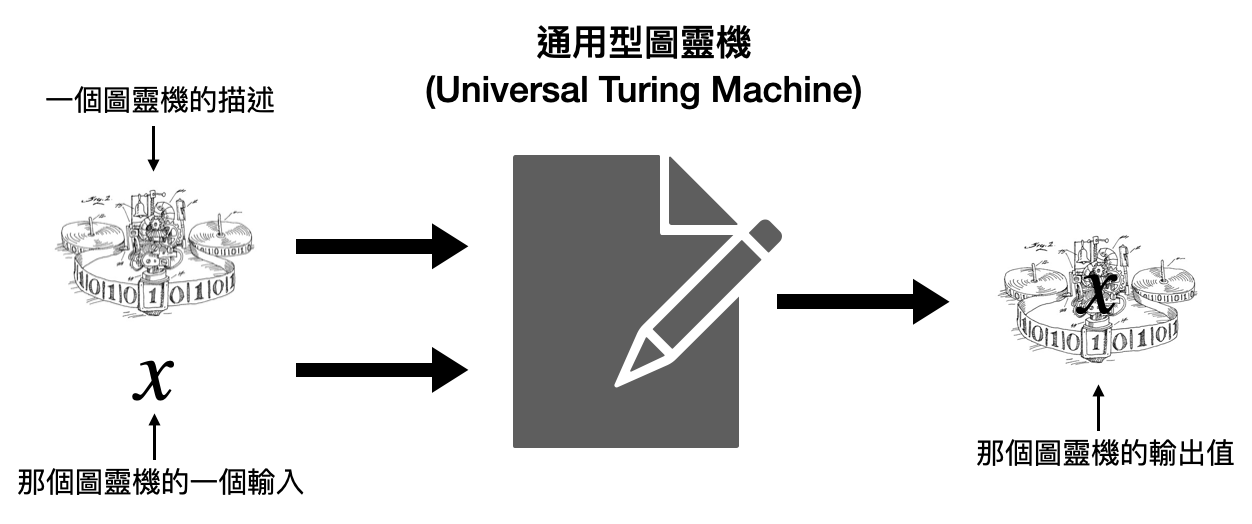
既然提到了圖靈完備的概念，一個很自然的問題就出現了：圖靈機可以模擬任何的圖靈機嗎？是否可以有一台特殊的圖靈機，它的輸入是一台圖靈機的參數和輸入，然後目標是正確地模擬這台圖靈機的計算過程。這種圖靈機又被稱為通用型圖靈機(universal Turing machine)。

Turing在他原始的論文中也告訴了我們，通用型圖靈機是存在的！這個結果有兩個重要的含義。首先，這告訴了我們圖靈機在數學上是個很自洽的定義。畢竟我們希望找到一個關於計算方法的數學模型，我們當然進一步希望這個數學模型可以刻畫住它自己能夠做到的計算。通用型圖靈機的存在就恰恰滿足了這個需求。接著，通用型圖靈機能夠做到“普遍性的計算”，可以讓人們在一台機器上就能方便地編寫程式然後進行各式各樣的運算。現代電腦中能讓我們執行各式各樣程式代碼的直譯器(interpreter)，正是扮演了通用型圖靈機的角色。

不可計算定理

目前為止，我們看到關於圖靈機的重要性，都是在說它能夠做到什麼。然而，有沒有什麼計算問題是沒辦法被任何圖靈機計算的呢？

答案是，幾乎所有的計算問題都沒辦法被任何圖靈機計算！

這個答案看起來似乎在表示圖靈機可能不是個好的數學模型，不然怎麼會大部分的計算問題都沒有相對應的圖靈機呢。然而如果我們回想一下關於計算問題的定義，一個計算問題是一個0/1字串的集合，就會發現其實大部分的計算問題基本上根本不會出現在我們的生活中！例如我們定義一個計算問題為隨機的決定一個0/1字串是否在集合之內，那麼我們可以分析有高概率這一個計算問題是沒有相對應的圖靈機的。而同時，這樣一個隨機的計算問題根本不會是平常生活中我們會在意的！

這時，一個比較正向的猜想可能是，也許現實中我們會在意的計算問題，應該都有個圖靈機可以計算它吧！？然而，Turing發現其實並不是這麼一回事！

存在一個很容易描述的計算問題，任何的圖靈機都無法計算它。

而這個“很容易描述的計算問題”，是「停機問題(Halting problem)」。問題的定義很簡單：輸入是一台圖靈機的描述以及一個它的輸入，計算的目標是回答這台圖靈機在接受了這個輸入後，是否會在某個時刻停下來，還是會無止境地運算(例如一個無限迴圈)。

不可計算定理乍看之下似乎打碎了Church-Turing論題的根基，然而實際上並非如此。因為人們發現，即使我們可以從不可計算定理以及其推廣中找到許多容易描述的計算問題，無法被任何的圖靈機計算，但同時我們也實在想不到有任何其他的計算方法可以計算這些問題！也就是說，這些計算問題看起來在現實世界中也的確是沒有一個計算方法可以解決的。

在走了這麼長一段路之後，Turing用圖靈機的定義，以及對Church-Turing論題的信仰，正式粉碎了Hilbert對可判定性問題的盼望：不是所有計算問題都有個計算方法可以判定它的。也許Hilbert的擁護者會覺得，停機問題又不是什麼自然的計算問題，也許它只是個特例？在不可計算定理問世之後，數學家透過本書第三章中會深入提到的“歸約方法”，展示了許多很自然的計算問題都仍然無法被任何圖靈機判定，例如著名的“丟番圖問題(Diophantine problem)”。

總結

在本章中，我們使用數學這個最抽象的語言，從最底層的數位訊號與二元表示，看到簡單的編碼方式如何具有豐富的表達能力。接著，我們見識到形式語言如何消弭語義上潛在的矛盾，成為了計算問題的數學定義。更進一步，Turing提出圖靈機這個數學概念，在Church-Turing論題的背書之下，電腦科學家相信了所有現實世界中可行的計算方法，都可以被一台圖靈機模擬。在這些根基之上，我們終於能夠回答大數學家Hilbert的可判定性問題，不知道該高興還是難過，Turing的不可計算定理告訴了我們，就算是像停機問題這樣如此容易描述的計算問題，都無法存在一個圖靈機計算它。

在下一章，我們將看到如何從不可計算定理的餘燼中，探索不同的計算方法和不同的計算資源如何影響計算的能力。

延伸閱讀

教科書：

內文提及的論文：

科普書籍、小說或電影：