Chapter 2
Computational Models and Computational Resources
Electronic computers are intended to carry out any definite rule of thumb process which could have been done by a human operator working in a disciplined but unintelligent manner.
Alan Turing
圖靈機除了為電腦/計算機的實作建立了數學基礎之外,更是替一個新的數學分枝打開了一扇大門,而這個領域就是計算理論(Theoretical Computer Science/Theory of Computing)。
顧名思義,計算理論是個探討關於計算的理論學科。深受其數學和邏輯根源的影響,其方法論奠基在抽象模型和數學證明之上。半個多世紀以來,計算理論不但延伸了圖靈機,廣泛的探討了不同計算模型和計算資源的能力極限,同時也漸漸開始提供其他領域(例如經濟學、物理學、生物學等等)不一樣的思考角度。
演算法
在上一個章節提到的圖靈機就像是個全能的幫手,不管你想做什麼事情,只要把每個步驟的細節都想清楚,然後把這些步驟轉換成圖靈機的語言,就能夠請它幫忙搞定你想做的事情了。
然而,即使是簡單的加減乘除運算,翻譯給圖靈機也將會是一個非常繁瑣且痛苦的過程。其根本原因在於圖靈機只能做非常基本的操作。想像如果你只會100個基本的英文單字,然後想要在美國的餐廳點菜。我相信你是做得到的,但是受限於可以用的單字量,點餐的過程將會變得非常冗長。
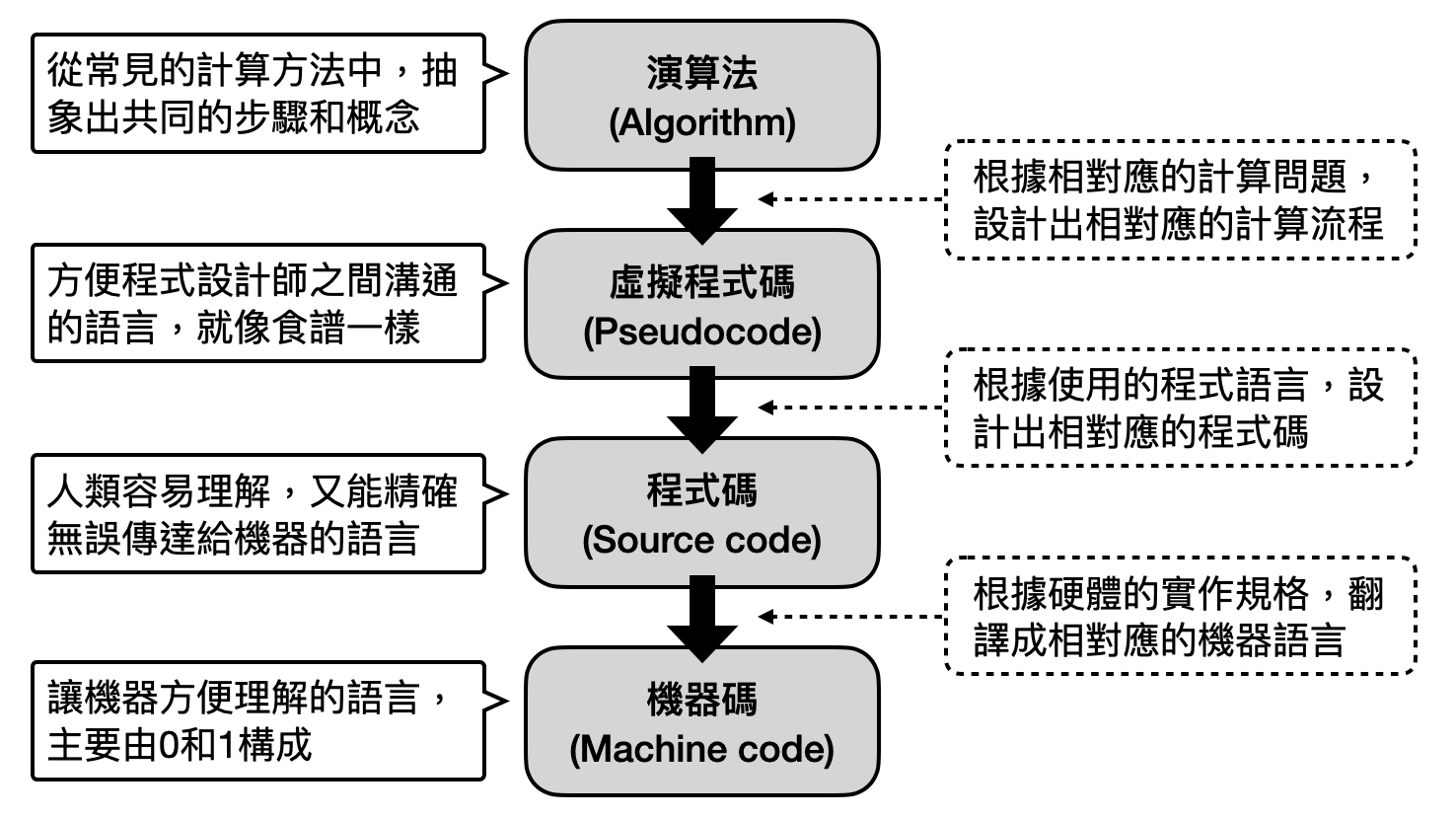
於是在實務上人們開始將電腦的實作層次化,建立許多中間的語言,讓使用者可以根據不同需求在不同層次編程。像是一般人會接觸到程式語言,需要經過多層步驟才能轉換到最底層機器看得懂的指令。
在這些程式語言之上,又有一群人開始思考不同程式代碼之間的相似性為何,做紅燒肉的程式是不是稍加修改就可以用來做蔥爆雞丁?於是「演算法(algorithm)」的概念就應運而生了!在不同的計算目標和程式實作中,類似的步驟或概念可能會以不同的面貌出現,但在數學本質上這些不同的實作其實都使用了同樣的想法,而我們稱之為演算法。
暴力算法
相信大家如果有玩過電腦闖關或是解謎遊戲的話,一定都遇過卡關的時候吧!到底要跟哪個隱藏的人物說話得到神秘線索,該如何巧妙的找到正確的移動順序。在百思不得其解時,常常莫名其妙地發現自己又再重複曾經做過的嘗試。
這時候,一個聽起來非常蠢,但是基本上一定有用的方法就是:系統性地把所有可能性試過一遍。既然電腦遊戲可以操作的範圍是有限的,總有一天我們會試到正確答案的!而這樣的解題破關方法,又被稱為「暴力算法(brute-force algorithm)」。想像一下使用這種方法來打遊戲,是不是真的很暴力呀!
暴力算法看起來這麼太暴力,怎麼會有人想用它呢?這樣不是很反智嗎?的確,當一個計算問題的”搜索空間(search space)”很大的時候,暴力算法大概需要跑到天荒地老。例如19乘19路的圍棋,它的每一步都有幾十幾百種可能,暴力算法根本無法算超過三五步。
不過,當一個計算問題的搜索空間沒有很大時,暴力算法或許不算是個太差的方法!畢竟暴力算法在實作上非常簡單,只要把所有可能性都嘗試一遍就好,不需要什麼其他複雜巧妙的思考。所以當眼前有三種蛋糕款式要選作為母親節的禮物,與其花一堆時間糾結半天,如果荷包允許,倒不如三個都買了,這樣媽媽說不定更開心呢!
貪心算法
想像你來到了一個新的城市,從機場租了車之後,你打算直接回旅館好好休息一下。然而由於網路還沒開通,沒辦法使用手機導航,你只能用離線模式的地圖嘗試找到又短又快的路線。剛搭完飛機非常疲憊的你,很懶得花功夫找到最快的路線,只要路線不要太慢其實都可以接受。這時候,有沒有什麼懶人找路法能夠輕鬆地幫你找到一條不太差的路線呢?
一個最簡單的方式,可以是直接選一條大約往旅館方向的道路出發,一旦遇到了叉路,都選擇在地圖上看起來是前往旅館的方向。雖然很有可能不幸遇到死路需要回頭,但如果這座城市的都市規劃做得不錯的話,這樣的導航方式應該是不會太差吧!?
這種做選擇和計算的方式,又被稱為「貪心算法(greedy algorithms)」,顧名思義,就是在做一連串的決策,每次都選對於總體目標來說最好的選擇。如此一來,省去了許多費盡腦汁計算最佳策略的心力,也不用像暴力算法一般把所有情況都試一遍,甚至在許多時候,貪心算法的結果也都還蠻不錯呢!
然而,貪心算法有時候也有可能表現得很差。想像你看到一條高速公路然後很開心地開上去,卻發現到下一座城市之前都沒有出口,那是不是欲哭無淚了呢?
二進位搜索法
小時候和家人出去玩的時候,常常為了打發坐車等車的時間,玩一些猜數字小遊戲。其中最簡單的大概就屬其中一個人在1到100之間選一個數字,當另外一個人猜了之後,告訴他猜的數字比想的數字大還是小,直到猜中為止。不知道讀者當年如果玩過這個小遊戲的話,會是用什麼方法來猜數字呢?
一個方法可能是心有靈犀法,因為對跟你玩的人太熟悉了,所以一眼就看出他心中在想什麼數字。不過如果沒有任何其他的資訊時,有沒有什麼方法可以盡可能地減少猜的次數呢?
許多人可能會想到以下的策略:首先在1到100的正中間選個數字,也就是選50。如果是大於50的話就在50到100正中間選下一個數字,如果是小於50的話則是在1到50正中間選下一個數字,以此類推。從下圖中我們可以這個“演算法”背後的圖像。你能看出這樣的猜法可以保證在多少步內一定可以猜到正確的數字嗎?
這個演算法又被稱為「二進位搜索法(binary search)」。從上圖中,我們可以看到二進位搜索法背後的精神是將一個大問題拆解成比較小,但在本質上相同的問題。以上面的猜數字遊戲為例,我們將原本要在1到100之間猜數字的問題變成了在1到50或是在50到100之間猜數字的問題。如果我們能夠很平均的把問題做拆解,就可以盡可能地讓最壞的情況都還是能夠被迅速地解決。對於猜數字遊戲來說,不管背後的數字是什麼,二進位搜索法都可以在七步之內猜出來!
分解戰勝法
一旦學會了二進位搜索法之後,猜數字遊戲可能就變得太無趣了,讓我們來玩難一點的遊戲吧!現在給你一堆不相同的數字,請你在最短的時間內找出這些數字的中位數(也就是依照大小排序好之後,在正中間的數字),你會怎麼做?最直接的方法就是把這些數字先排序好,這樣就可以明確地知道中位數是什麼。那該如何把數字做排序呢?
最簡單的方法可能是先把所有數字看一遍,找出最小的數字。接著再重新看一遍,找出第二小的數字,然後以此類推。這樣的演算法又被稱作為泡沫排序法(bulbble sort),非常容易理解和實作,但是因為每次都要把剩餘的數字在全部看一遍,所以一旦數字多了之後,就會變得非常慢(在本章後半段我們會更具體地討論怎麼比較和分析演算法的速度)。
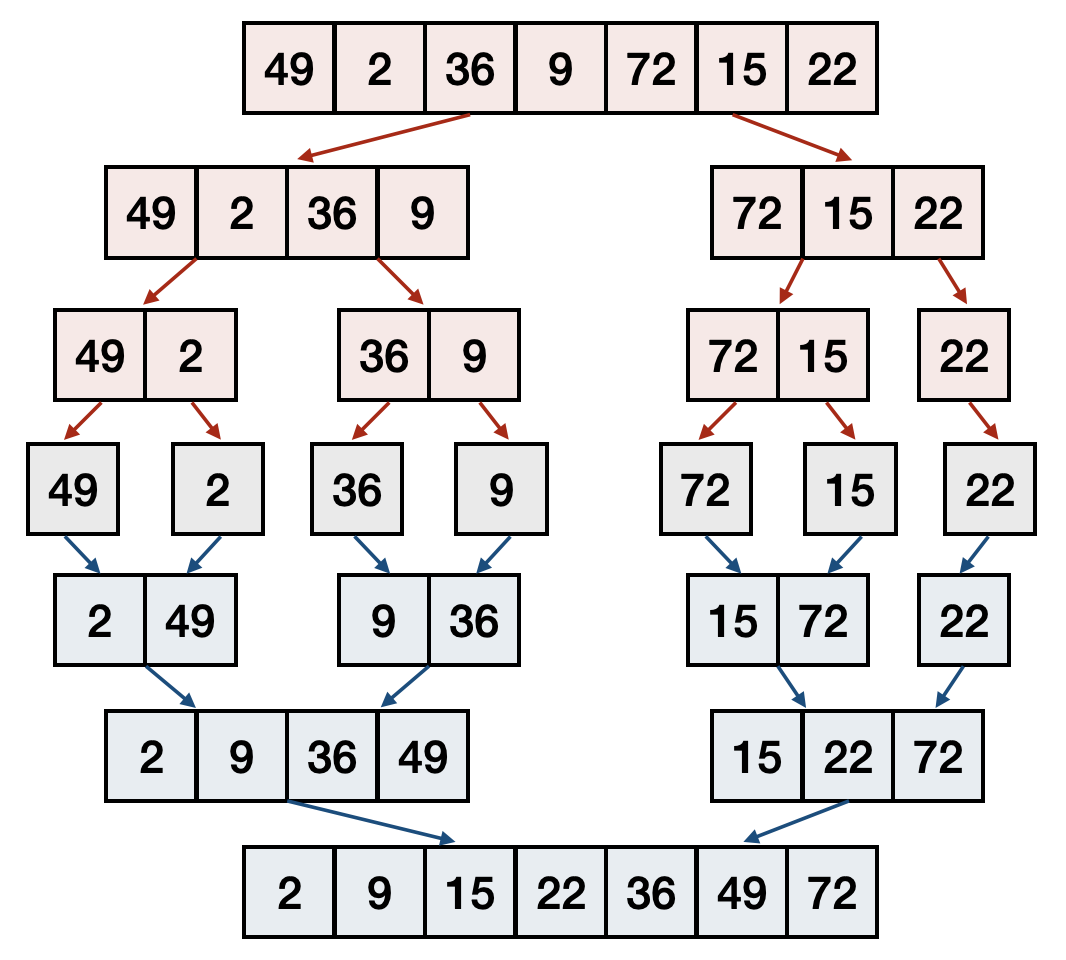
所以我們知道當需要排序的數字不多時,簡單的方法像是泡沫排序法就可以輕易解決。當數字很多的時候,我們是不是也可以學習二進位搜索法的精神,先把這些數字分成一堆一堆的,分別快速地排序好之後,再用某種方法合併起來呢?如果合併的方法不會太麻煩複雜,這樣說不定比直接使用泡沫排序法還要快呢!
這樣先把問題切成小份,分別解決之後,在合併起來的方法又被稱為「分解戰勝法(divide and conquer)」。以數字排序問題來說,當我們有兩堆已經排序好的數字之後,在找最小的數字時,就不需要把所有數字都看一遍了!你有發現為什麼了嗎?沒錯,因為這兩堆數字都已經照大小順序排好,在它們之中最小的數字一定會是各自分堆中最小數字的其中一個。如此一來,在找最小數字時,只要看兩個數字就足夠了!
在平常工作、學習、或是生活之中,是不是也有很多機會可以利用分解戰勝法來把看似複雜的任務簡化?而回到最一開始的中位數問題,在之後的章節我們會看到目前已知最快排序$n$個數字的演算法需要$\Theta(n\log n)$(本章後半段將會解釋這個符號的意思),如果只是要找出中位數的話,有沒有什麼更快的方法?
動態編程法
讓我們來玩一個默契小遊戲,兩個人各自寫下一串數字,然後拿出來互相比對,看有多長的部分是一樣的。舉例來說,我選了28723,你選了82743,那麼這兩串數字之間的”最長子序列(LCS, longest common subsequence)”將是273。假如現在我們各自寫下了100個數字,該如何找出最長子序列呢?
首先,我們當然可以使用暴力算法,把所有可能的子序列都比較一遍。然而這樣似乎太費時了,有沒有什麼更聰明更有效率的方法呢?
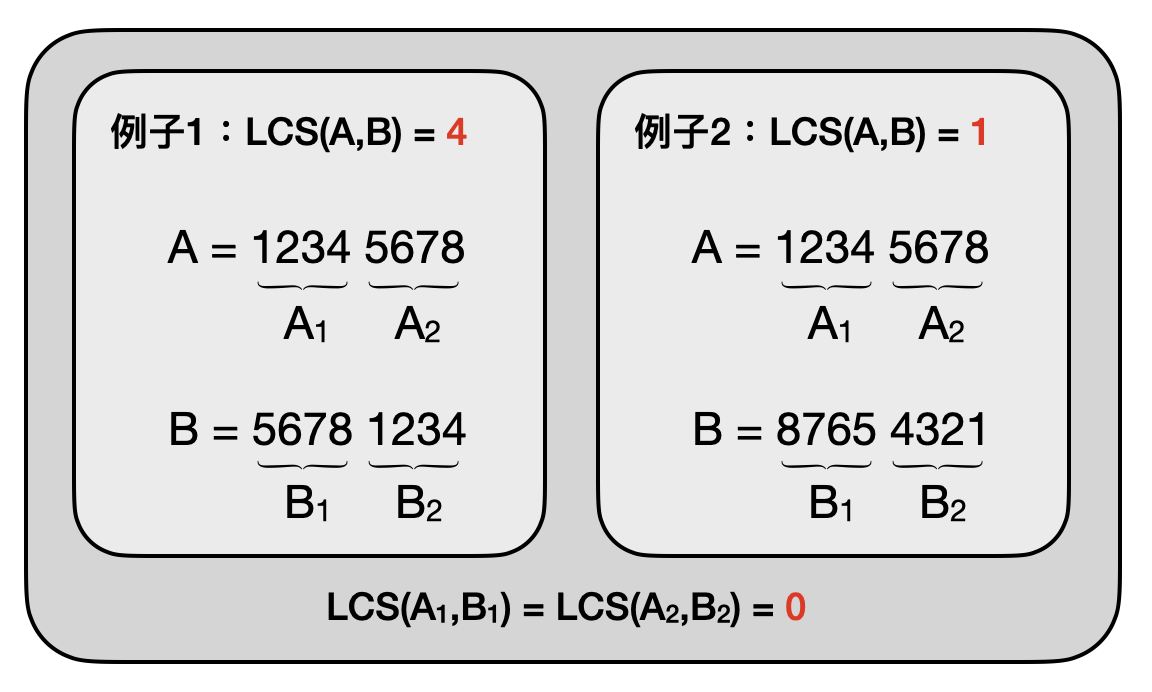
要不讓我們先用之前分解戰勝法的概念來試試看,把輸入的兩個字串分解成小的字串,找到各自的LCS後,再看看可不可以從中知道原本大字串們之間的LCS。不過這時候麻煩出現了,如果原本字串的LCS並不包含在小字串們的LCS內,那我們將無法透過這些小字串們的LCS回推出大字串的LCS。在下圖的兩個例子中,我們可以看到當兩組小字串的LCS長度都為0時,原本字串之間的LCS長度既可能是4也有可能只是1!
雖然分解戰勝法無法算出LCS,不過我們可以從它的失敗中學習。從上述的例子中,我們可以發現主要的癥結點在於,一旦原本大字串的LCS橫跨了不同的小字串,就很有可能不再是小字串的LCS。於是當我們只考慮從大字串中切出互不重疊的小字串時,就很容易在一開始就把真正的LCS忽視掉了。
所以一個可以馬上改進的地方,就是考慮各種不同小字串的切法,然後計算它們之間的LCS,也許這樣就可以提供足夠的資訊讓我們回推出大字串的LCS?這樣透過計算一些相互重疊的子問題,然後由下而上拼湊出最終答案的演算法,又被稱為「動態編程法(dynamic programming)」。
如果你已經昏頭了,沒有關係,具體想要把動態編程法的細節搞清楚,的確需要靜下心來好好分析各種情況。然而動態編程法最核心的大概念其實很簡單:將問題切成小的子問題,並且找到一種辦法由小到大、由下而上利用已經算出來的答案,來解決越來越大的子問題。如此一來,即使這些子問題可能互相重疊,我們還是可以透過系統性地算出“所有”比較小的子問題,然後再用這些答案幫忙算出比較大的子問題。
某種程度,動態編程法還蠻像是在學校學習知識的,一開始總是會要先學一些看似沒用的基礎技術和習題,但是隨著時間的累積,開始可以混用不同的基礎技術處理一些稍微複雜的問題。如果融會貫通了之後,一旦遇到了沒看過的新問題時,與其把問題一步一步地拆解成為多個瑣碎的小問題,不如直接利用之前建構起來的知識,輕鬆地把問題解決。
對於一個字串$A$,我們把它的第$i$個數字稱為$A_i$,然後把前$i$個數字組成的子字串稱為$A_{1:i}$。讓我們把$A_{1:i}$和$B_{1:j}$之間的LCS的長度標註為$LCS(i,j)$。如果能夠計算所有$LCS(i,j)$,我們就可以輕易地知道$A$和$B$之間的LCS了(把$i$和$j$設為A和B的長度)。那我們該如何系統性地計算出所有的$LCS(i,j)$呢?
當$i=j=1$的時候,我們只要比對$A$和$B$的第一個數字是否相同即可。當$i=1$,然後慢慢把$j$變大時,我們可以發現$LCS(1,j)$絕對不可能會變小。而這個觀察適用於任何固定住的$i$:$LCS(i,j)$
不會因為$j$變大而變小。更進一步,一旦我們知道$LCS(i,j)$是什麼,在計算$LCS(i,j+1)$時,只要檢查$B$的第$j+1$個數字會不會讓共同子序列變長就好了!至於該如何檢查$B$的第$j+1$個數字會不會讓共同的子序列變長呢?我們可以發現只有以下幾種可能性:
- $A_i$和$B_{j+1}$相同時:我們可以確保$A_{1:i}$和$B_{1:j+1}$的LCS中最後一個數字可以是$A_i$和$B_{j+1}$。於是,去掉這最後一個數字後,$A_{1:i}$和$B_{1:j+1}$的LCS將會是$A_{1:i-1}$和$B_{1:j}$的LCS。也就是説,$LCS(i,j+1)=1+LCS(i-1,j)$。
- $A_i$和$B_{j+1}$不同時:我們可以知道$A_{1:i}$和$B_{1:j+1}$的LCS並不會同時包含$A_i$和$B_{j+1}$。也就是說,$LCS(i,j+1)$會是$LCS(i,j)$和$LCS(i-1,j+1)$之中比較大的那個。
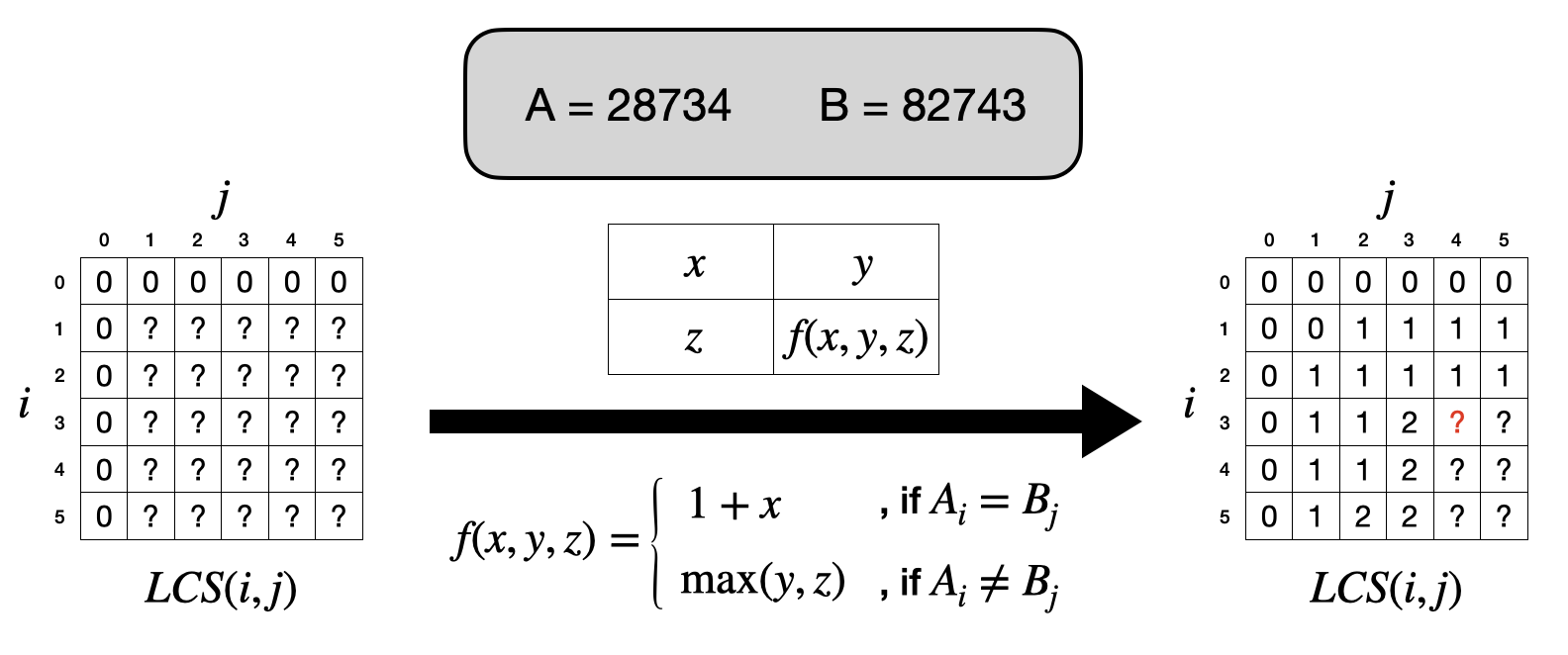
上面的觀察可以被整理成為一個句子:在計算$LCS(i,j)$時,只要知道$LCS(i,j-1)$、$LCS(i-1,j)$、$LCS(i-1,j-1)$這三個就好了!也就是說,如果把計算$LCS(i,j)$想成是要把圖左裡面下
方的表格填滿,只要從左上角慢慢往右下角循序漸進地根據上面的規則更新答案的話,就可以完成了!
整數編程法
目前為止介紹過的演算法,除了暴力算法之外,基本上都是提供一個大方向的概念,實際遇到問題時,還需要根據情況發揮一些靈感稍做變化,有時候甚至不見得可以使用。畢竟人的創意和靈感不是天天都有的,有沒有什麼演算法,可以免除掉這種不確定和變化性,讓我們機械性和系統性地找出還不錯的計算問題呢?
想像在中學時解物理課上的力學習題,很多時候題目都會有些小巧門,可以簡單迅速算出答案。然而如果在考試時突然緊張想不到這些小技巧,有沒有什麼比較慢,但是一定可以保證算出答案的方式呢?沒錯,就是把習題中所有的物體、限制條件等等全部列下來,接著在系統性地把這些等式與不等式解開。如此一來,只要學會怎麼機械性地解出給定的等式與不等式,就可以所向披靡地解開任何的物理習題了(只不過速度可能會很慢…)!
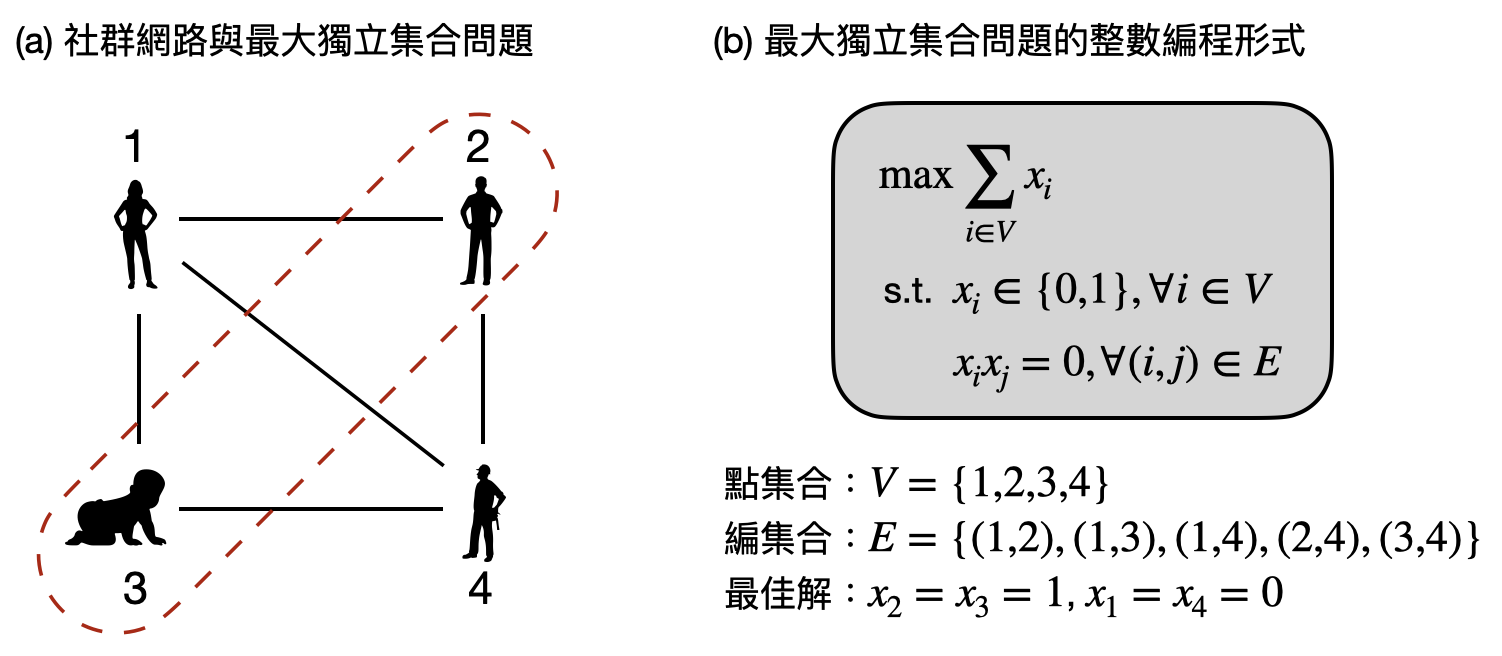
「整數編程法(integer programming)」就是一個如上述可以有個標準程序、機械性解決問題的演算法,而且可以更廣泛的應用在非常多的計算問題上。讓我們用一個簡單的例子來解釋整數編程法的概念:假設現在你有個社群網路的好友連接圖(例如下圖(a))中告訴我們任意兩個用戶是否為好友的資訊。現在如果要你找出一群互相不是好友的人,並且越多人越好,該如何做到呢?這個計算問題,又被稱作「最大獨立集合問題(maximum independent set problem)」。接下來我們將展示如何把這個問題寫成整數編程的形式,如此一來就可以用一個整數編程法的通用演算法解決了!
現在讓我們把每個用戶從$1$到$n$編號,並且用變數$x_i$來表示用戶$i$是否被選擇(到你要找的那群互不認識的人),那麼上述的最大獨立集合問題將等價於圖(b)中的整數編程問題。
這樣聽起來整數編程法是不是也太厲害了,竟然可以用來解決大量的計算問題(尤其是組合優化問題),那不是遇到什麼問題就用整數編程法就好了!?當然沒有這麼好的事情,雖然許多計算問題可以被轉換成整數編程的形式,然後使用通用的演算法解決,然而這個通用的演算法在大部分的時候都是非常沒有效率的!
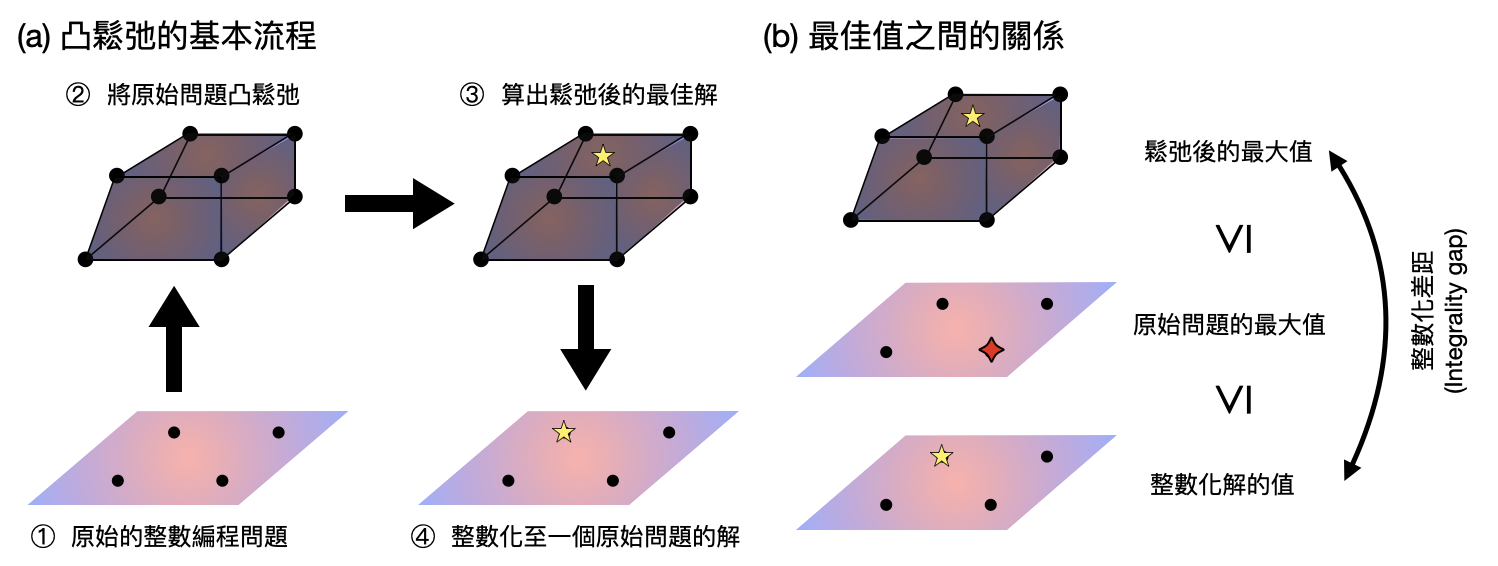
如此一來實在有點可惜,幸好電腦科學家們很有創意,發現整數編程的形式雖然沒辦法有很快的通用演算法,然而我們可以透過用整數編程作為中間的步驟,並在之上進一步的把問題轉換成擁有快速通用演算法的形式!一類這樣做的方法被稱為「凸鬆弛(convex relaxations)」。
會使整數編程法沒有快速演算法的一個核心原因,就是其變數的取值是“離散的”。以上述最大獨立集合問題為例,變數$x_i$們可以取的數值為0或1。如此一來,通用演算法基本上需要乖乖的把各種變數可以取的值都試過一遍,沒辦法利用額外的代數或幾何結構來降低搜索的次數。
凸鬆弛的主要概念是將一個整數編程問題中變數的取值範圍,從原本離散的變成是「凸的(convex)」,這個新的計算問題將成為一個「凸優化問題(convex optimization)」。什麼是“凸的”,為什麼凸優化問題有快速的通用演算法?解決凸化的整數編程後,該如何對應回原本的整數編程問題?
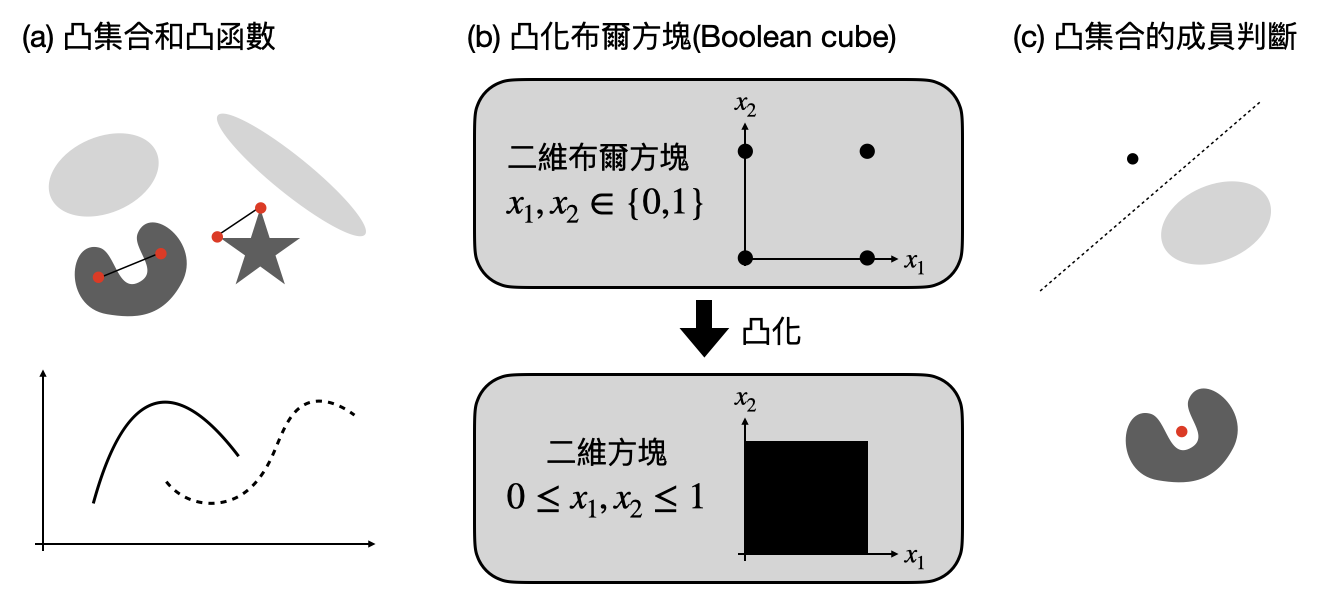
首先,“凸的”是個很有幾何直覺的數學概念:一個集合是凸的代表任兩點之間的連線都還在這個集合內。一個函數是凸的代表函數中所有等高集合都是凸的。上圖(a)有許多凸和非凸的例子。而凸優化(conver optimization)問題指的就是在一個凸集合上,最大/最小化某個凸函數的計算問題。上圖(b)中有個“凸化”非凸集合的例子。
為什麼凸優化問題可以有快速的通用演算法?一個核心的原因是其「成員判斷(membership identification)」非常容易:當一個集合是凸的時候,對於任何一個不在這個集合中的點,都會有一條線(或是更廣義來說,一個超平面)將這個點和這個凸集合分到兩邊!在數學中這是源自於Farkas引裡(Farkas Lemma),上圖(c)中有幾個簡單的例子提供直覺圖像。
不過,天底下沒有白吃的午餐,被凸化的整數編程問題,由於其取值空間(solution space)變大了,於是凸優化算出來的最佳值,通常都比原本的最佳值還要大很多(如果原本是最小化問題的話,那就是比原本的小很多)。因此,凸鬆弛通常只能幫助我們快速地給整數編程問題一個估計,並沒辦法完全的解決原始的問題。
計算模型
當提到計算模型時,可能許多人的第一反應是一台電腦或是一台機器。不過這邊所說的計算模型指的是一個數學架構,而這個數學架構可以實現出各台實際的機器。就像是“科學家”指的是所有從事科學行業的研究人員而非某個具體的人,一個計算模型描述了一類計算機器,具體的一台計算機器則會對應到用來解決某個計算問題。這樣聽起來有沒有跟計算問題和問題實例的差別很像呢?沒錯,為了要在數學上方便討論,數學家和理論電腦科學家不得不把這些平時很直覺的語言,變得有點饒口。
雖然說圖靈機是計算理論乃至整個電腦科學的基礎計算模型,然而根據不同的情況,人們也會研究一些其他的計算模型。這些數量眾多的計算模型,大致上可以分為以下三類:
比圖靈機更弱的計算模型:在圖靈機問世之前,有許多比圖靈機更弱的計算模型被提出來研究和討論。在這邊“比較弱”有很明確的數學定義:「如果有個計算問題可以被計算模型A解決但是不能被計算模型B解決的話,我們就會說B比A還要弱」。常見比圖靈機更弱的計算模型包含了前一個章節提到的DFA(確定有限狀態自動機)和正則表達式(regular expression)等等。
可能有些人會問,既然都有了更強的圖靈機了,為什麼我們還要研究這些比較弱的計算模型呢?主要有兩個原因,首先是在數學上,透過研究不同強度的計算模型,我們可以更瞭解不同計算步驟和計算問題的本質差異。例如,只擁有有限狀態數量的DFA是個非常弱的計算模型,連之前提到的“回文問題”都無法解決。其次就是在實務上,有時候我們並不見得需要像圖靈機這樣強大的計算能力,一些簡單的模型就已經足夠刻畫所需的計算,何必殺雞用牛刀?就像在做加減乘除運算的時候,只需要用到簡單的計算機就好了。
跟圖靈機等價的計算模型:在上一個章節提到了Church-Turing論題假設所有可行的計算,都有個相對應的圖靈機模擬。乍看之下圖靈機處在計算模型的金字塔頂端高不可攀,然而很有趣的是,數學家和電腦科學家發現有大量的計算模型其實是和圖靈機等價的!在這邊等價的意思很簡單:「如果任何一個計算模型A的實際機器都可以被一個計算模型B的實際機器模擬,且反之亦然。」。如果有個計算模型和圖靈機等價的話,我們就會稱之為圖靈完備(Turing-complete)。
有什麼計算模型是圖靈完備的呢?從Turing的老師Church提出的$\lambda$-calculus、所有常見的程式語言、到許多電玩遊戲,全部都是圖靈完備的!等等,這樣是不是有點奇怪,怎麼搞了半天好像所有計算模型都跟圖靈機是等價的,那為什麼我們要特別把圖靈機獨立出來討論呢?別忘了我們現在是在數學的世界,圖靈機的重要性在於它乾淨好操作的數學介面,讓我們很方便地分析各種計算相關的數學性質(在之後的篇幅很快會提到!),你能夠想像要用遊戲minecraft來作為計算模型的數學基礎嗎?(說不定這樣這個世界上會有更多的理論電腦科學家!)所以當下次有人跟你說他設計了一個圖靈完備的計算模型時,別被唬到了,你可以打開電腦裡面的power point告訴他這也是圖靈完備呢!
圖靈機的重要性在於它乾淨好操作的數學介面,讓我們很方便地分析各種計算相關的數學性質。
根據應用定義出的計算模型: 如我們一再強調,圖靈機雖然在數學上是最強大的計算模型(之一),然而平時不會有人真的百分之百照著原始圖靈機的定義去架設一台計算機。尤其是根據不同的情境,電腦科學家會更想要有計算模型可以精準的描繪相對應的應用。而這些不一樣的計算模型,有時候不太能夠直接和圖靈機做強弱的比較。在這邊我們將看到兩個經典的例子:線路(circuits)和通訊模型(communication models)
線路
現代電腦在工程中奠基於電晶體(transistors)之上。簡單來說,電晶體是一些微小的電子元件,能夠做簡單和基本的計算。透過把許多微小的計算串接起來之後,所形成的積體電路(integrated circuits)就變成可以做許多複雜的計算了!這好比在一個巨大的汽車工廠中,生產線上的各個員工就像小螺絲釘般,重複做一些簡單的零件組裝。雖然單一員工做的事情看起來非常簡單,然而整體來看所有員工可是共同製作了一台車子。
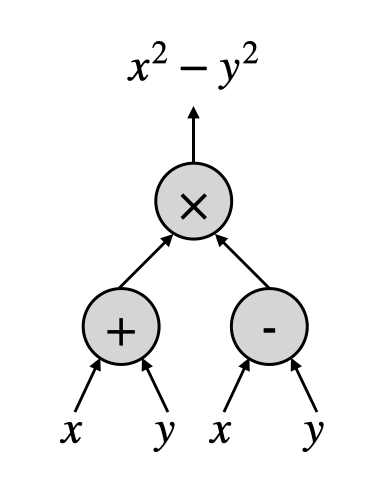
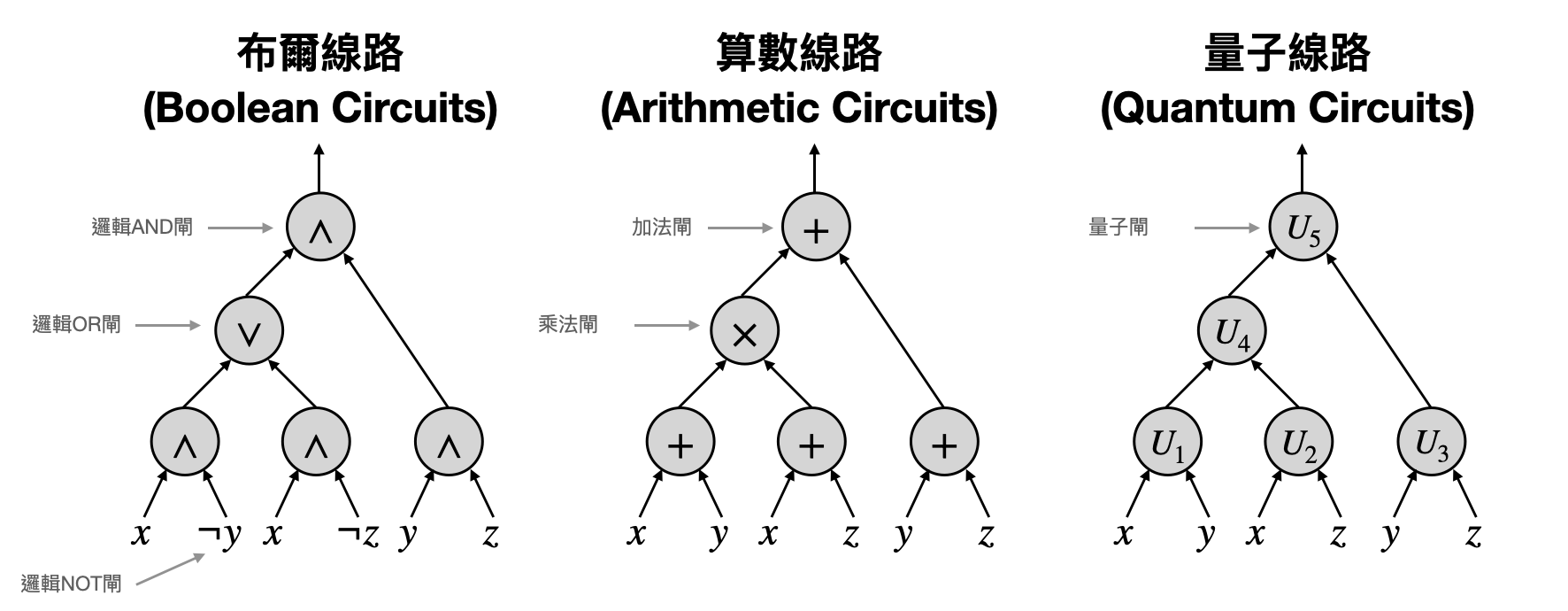
線路(Circuits),就是一類想要刻畫上述這種計算方法的計算模型。在一個線路中,會有許多的節點,代表著各個簡單的微小計算,例如把數字相加起來。節點之間則是由一些箭頭連接,標記著一個節點該把計算的結果傳到另外一個節點作為它的輸入。下圖提供了一個簡單的例子,用線路的方式計算了$x^2-y^2$。
節點有時候又被稱為“閘(gate)”,因為它就像是讓一些輸入的資訊進入,接著再把處理完的結果從另外一頭傳送出去。
根據閘可以執行的微小計算,我們可以定義出各種類型的線路。像是在上面的例子中,我們可以在閘上進行加減乘除的運算,這種線路被稱為算數線路(arithmetic circuits)。如果可以使用布爾(Boolean)邏輯運算(也就是0/1的邏輯運算),那麼這種線路就被稱為布爾線路(Boolean circuits)。如果閘可以進行量子計算,那麼這種線路就被稱為量子線路(quantum circuits)。
線路是最接近電腦工程上實現的數學模型,像是現在各個積體電路大公司,都會有專門的研發部門在研究如何使用更小更省能源的線路來實現某些計算功能。
而在數學上,線路和圖靈機有個本質上非常不一樣的地方:一個線路能夠計算的是具有固定輸入大小的計算問題,而圖靈機計算的是一個完整的計算問題。例如,將兩個數字相加,在一個線路上我們只能針對固定長度的數字(例如只能做三位數的相加),而我們可以輕鬆地用一個圖靈機來計算任意長度的數字相加。
不知不覺,我們又回到了之前一再強調有限和無限的差別:線路計算的是只有有限多種輸入的函數,圖靈機計算的則是一個擁有無限多種輸入的函數。這也造成兩者有點難相互比較。為了讓兩者能夠在同一個基準點上做比較,理論電腦科學家決定一次考慮無限多個線路而非單一線路,不過由於之中的細節討論將會過於瑣碎,所以有興趣的讀者可以參考延伸閱讀。
通訊模型
想像你和一個朋友正在討論作業,由於疫情的關係你們只能透過網路討論。你們想要比較一下各自算出來的答案相不相同,然而這是個非常複雜的程式作業,計算出來的答案檔案十分巨大,如果要上傳到網路然後下載做比較會花太多的網路流量和時間。你們該如何傳輸少量的訊息,同時又能夠很有把握地知道你們的答案一不一樣呢?
這樣的計算情境,又被稱作為通訊模型(communication models),是個看似簡單卻有大量理論應用的計算模型。
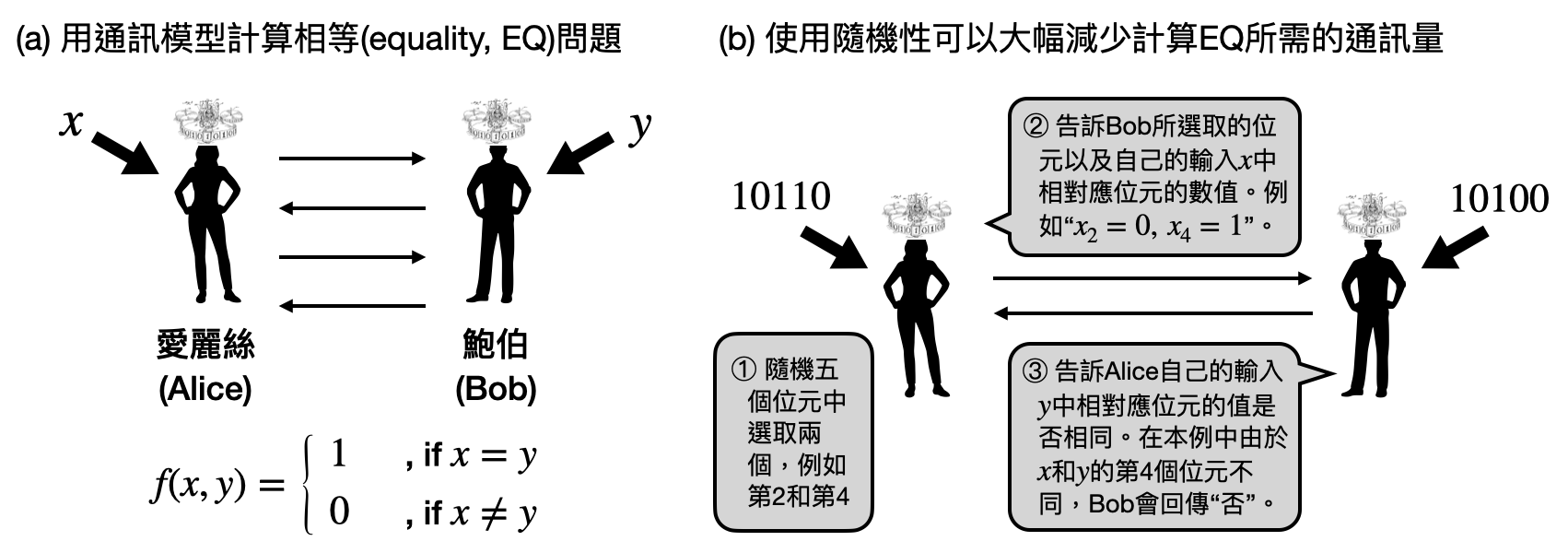
具體來說,在通訊模型中會有兩個或以上的參與者,通常他們會被稱作Alice和Bob。兩人共同的目標是是計算一個他們都知道的函數$f$,這個函數有兩個輸入$x$和$y$,會分別給Alice和Bob。以上述的例子來說,$f$是個檢查兩個輸入是否相等的函數,也就是説$f(x,y)=1$當且僅當$x=y$。Alice和Bob會各自收到輸入$x$和$y$,然後他們可以傳輸一些訊息,最後的目標是要計算出$f(x,y)$。
由於兩人彼此不知道對方的輸入是什麼,最簡單的方式就是其中一人把自己的輸入傳給對方,這樣對方就可以直接算出$f(x,y)$。然而如果$x$和$y$十分的巨大,有沒有更有效率的方式傳送訊息呢?
在通訊模型中,相對應的演算法又被稱為“協議(protocol)”,一個協議會告訴Alice和Bob該如何根據各自的輸入和收到的訊息,來決定接下來要傳送什麼訊息,以及該如何輸出最後的答案。注意到在收到計算問題的輸入之前,兩人需要先訂下來所要使用的協議是什麼,就像設計演算法之前我們不知道將會收到什麼輸入一樣。
讓我們回到上述檢查兩人輸入是否相同的函數,它又被稱為相等函數(equality)$EQ$,而通常我們會先訂下輸入的長度為一個變數$n$,然後討論輸入長度為$n$的相等函數$EQ_n$可以有什麼樣的通訊協議。很遺憾的是,我們可以證明任何一個計算$EQ_n$的協議都需要傳長度至少為$n$的訊息,不然這個通訊協議就一定會在某組輸入上得出錯誤的計算結果。然而,如果我們讓計算協議中使用一些隨機性的話,就可以大幅度的減少需要傳輸的訊息量(也就是總共需要傳輸的訊息的比特數)!有興趣的讀者可以參閱上圖(b)的解釋。
計算資源
在上個世紀初期,Hilbert提出的可判定性問題,讓數學家開始關注一個計算問題是不是能夠有個相對應的計算方法。隨著圖靈機的誕生和Turing重要的不可計算性定理,人們對於可不可以被計算性(computability)有越來越充足的了解。緊接著電腦的誕生和普及,大家開始漸漸將研究的方向轉為分析一個計算問題所需要的計算資源為多少。
什麼是計算資源(computational resources)呢?當你執行一個程式時,大概不會希望連簡單的加減乘除都需要花上一整天的時間吧?所以“時間(time)”是一個我們會在意的計算資源。出門遊玩時,一個讓人不想遇到的情況就是手機的記憶體容量滿了,無法存新的照片。因此“空間(space)”也是個不可或缺的計算資源。除此之外,還有眾多如隨機性(randomness)、非決定性(non-determinism)、量子性(quantumness)、互動性(interaction)等等計算資源。以下讓我們看看幾個例子。
非確定性
在我們日常生活中,時常會有所謂“靈光一閃的時刻(Aha moment)”。例如在解一個困難的數學題目、創作藝術或是討論計畫的時候。然而,圖靈機和演算法看起來通常只能很死板地跟隨一些固定的過程做計算,我們是否能夠把這樣靈光一閃的能力加到圖靈機之中呢?
我們可以來認真思考一下這些靈光一閃的想法,有哪些共通點。首先,靈感雖然來得突然,但並不是所有想法都是好的靈感。再來,一個好的靈感,基本上是要能夠被快速驗證的。如果解開了一道數學題目,通常都是有個容易檢查的證明。一件有創意的藝術品,往往也是一眼就可以被大家認可。這些觀察告訴我們,就算不知道靈感的起源是什麼,但可以確定的是,一個好的靈感在被提出之後,是能被簡單且迅速驗證的。
於是,在數學上理論電腦科學家試圖將靈感刻畫為一種計算資源,與一般具有固定運轉規則的圖靈機不同之處,是在於其計算過程中可能會有些如同靈感一樣的不確定性。為了做區別,我們稱原始的圖靈機為「確定性的(deterministic)圖靈機」,然後把具有額外靈感的圖靈機稱為「非確定性的(non-deterministic)圖靈機」。
非確定性刻畫了能夠被簡單且迅速驗證的靈感。
從小到大你是否曾經有過幾次“文思泉湧”或“靈感爆棚”的經驗?在那樣的狀態之下,不管是寫文章或是做習題,都不會像平常一樣糾結用字遣詞或是煩惱到底要用哪個公式,腦中似乎有個聲音告訴你下一個字要寫什麼。這種計算過程中出現的腦中聲音,在數學上被描述成所謂的「非確定性步驟」。
另一個常見的情景則是,每當讀到絕妙的好文章或是看到非常有創意的畫作時,不需要花太多力氣就能迅速欣賞這些充滿好靈感的作品。這種能夠被輕易驗證優劣的特性,在數學上被所謂的「證明與驗證遊戲」刻畫。
以上兩種“靈感”出現的方式,竟然在數學上是等價的!不過在理解這個深層關係之前,我們需要先認識非確定性步驟和證明與驗證遊戲。
非確定性步驟: 在確定性的圖靈機中,計算過程被一個確定性的轉換函數所描述。“確定性的”在這邊指的是,一旦知道了目前所在的狀態以及紙帶上標寫的符號,那麼轉換函數的輸出就會被完全確定下來。想像你站在一個路口,決定要往左還是往右走。如果你做決定的方式是“確定性”的話,那麼一旦所有的初始狀況是相同的,你所做的決定也會是一樣的。
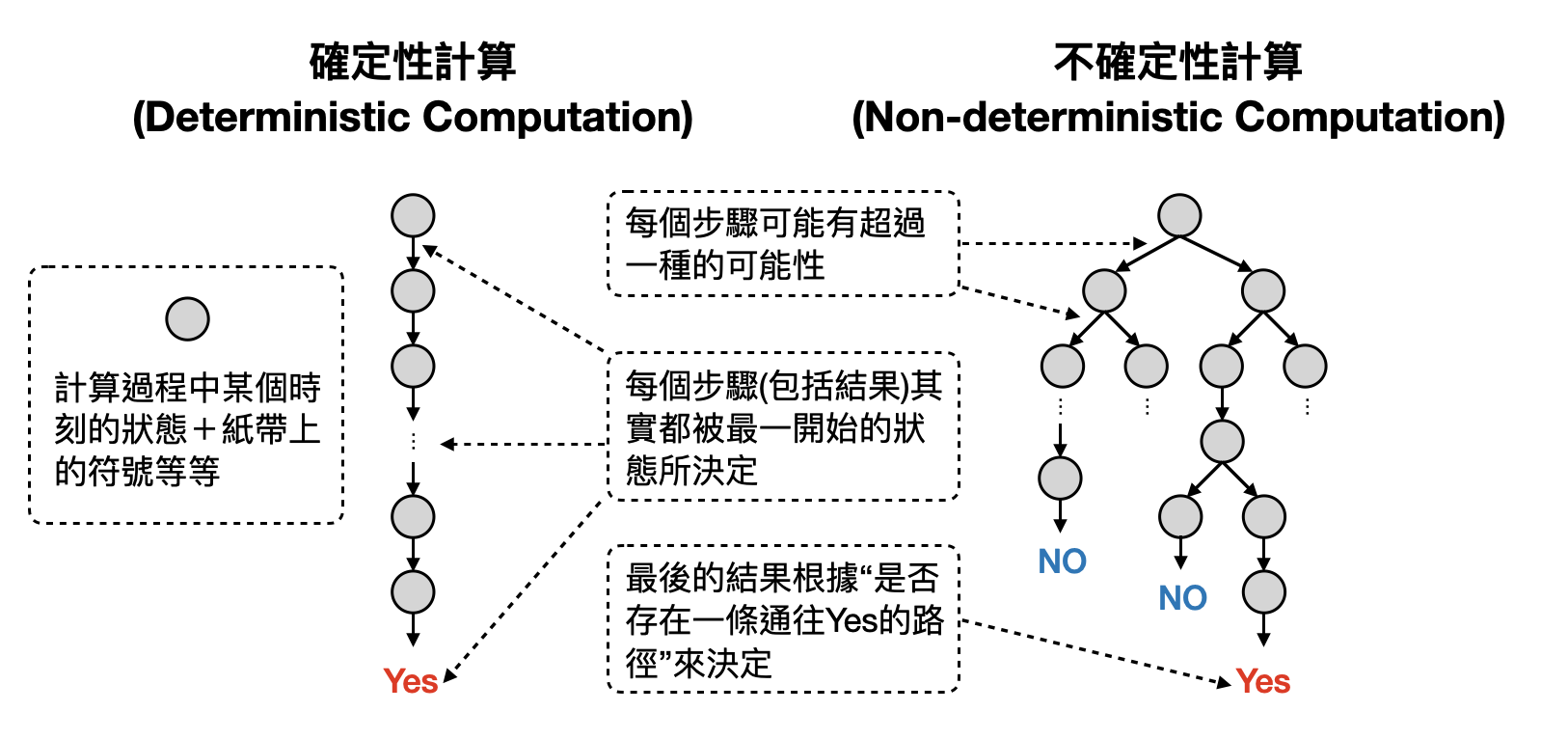
那什麼是非確定性的步驟/轉換呢?延續上一段交叉路口做抉擇的例子,非確定性的決策方式將不再只會完全根據當下的狀態,而是會有個如同靈光一閃的時刻(Aha moment),選擇了其中那條比較好(可能會通往好的結果)的道路。從下圖中我們可以再更加具體化目前為止的討論,讓我們將圖靈機目前的狀態和紙帶上的符號看成是一個整體,並以灰色的圓圈表示。於是圖靈機計算的過程,就可以被想成是灰色圓圈從一個轉移到另外一個。這樣來看,是不是就變得像上述交叉路口的例子了。讓我們來看看確定性計算和非確定性計算,分別會對應到什麼樣子的地圖。
在每一個計算步驟中,轉換函數會將圖靈機目前的狀態和紙帶上的符號約略修改。於是對確定性的計算來說,對應到將這一步的灰色圓圈,對應到下一個灰色圓圈。如此下來,就連計算的最終結果也是被最一開始的灰色圓圈就完全決定下來了。也就是說,在確定性計算中不會有任何交叉路口,所有的道路都是直接通往結果!
對非確定性計算來說,每個步驟可能會去到的灰色圓圈將可能不只一個,也就是會有許多時刻要面臨交叉路口做選擇。然而,每條路徑最終可能會走到不一樣的結果(在決策型問題中,有兩種結果:Yes/No),那麼該如何決定非確定性計算的計算結果呢?根據最一開始提到非確定性和“靈感”的關聯,一旦有了靈感(非確定性)的幫助,我們將能在遇到交叉路口時,每次都選到了通往好結果的道路,於是電腦科學家將非確定性計算的結果定義為“是否存在一條通往Yes的計算路徑”。
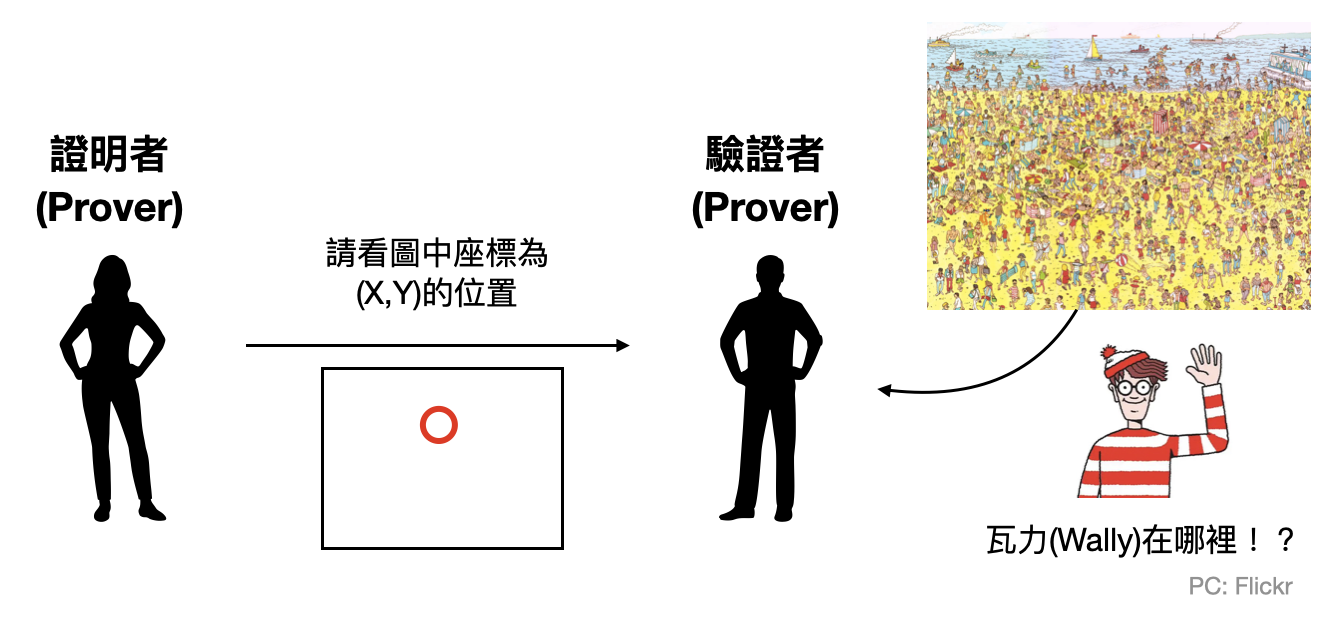
證明與驗證遊戲: 非確定性計算也可以從“證明與驗證遊戲(prover and verifier game)”的角度來理解。我們可以把非確定性圖靈機想成是給一個確定性圖靈機多了一種特殊的輸入:「證明(proof/witness/certificate)」。而非確定性的計算就是在檢查這個證明是不是正確的。
舉例來說,在著名的尋找瓦力(Where’s Wally)這個遊戲中,玩家需要在如上圖的複雜圖畫中,找出瓦力在哪裡。如果要你設計一個演算法來尋找瓦力,可能唯一的方法就是暴力地把整張圖的每個角落都檢查一遍。然而如果演算法有了非確定性,那麼相對應的證明就可以是瓦力所在的位置,而演算法需要做的就只是確認在那個位置上是否真的有瓦力。
為什麼這兩種關於非確定性計算的觀點是等價的呢?有興趣的讀者可以試著根據下一章提到的Cook-Levin定理來證明兩種觀點的等價性。
總結來說,非確定性這個計算資源,是電腦科學家試著用來描繪平常我們體驗到靈光一閃的瞬間。我們當然總是能夠把非確定性計算中所有的計算路徑都嘗試一遍,進而找出答案。不過這樣暴力的計算方法很明顯需要花上很多時間。該不會非確定性/靈光一閃的計算能力的確可以提供很大的加速?這個大哉問是理論電腦領域裡最核心的未解之謎,我們將會在不久後的段落提供更完整的介紹。
隨機性
擲銅板除了在不知道如何做決定時能夠幫上忙之外,往往也能讓人設計出更快更好的演算法!讓我們看看下面這些例子:
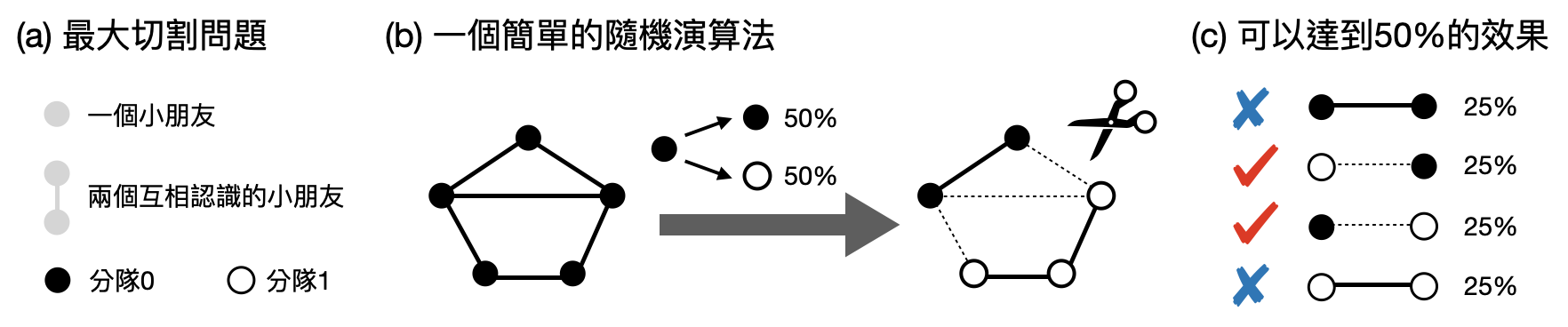
最大切割(Max cut): 想像現在你需要負責將一群參加營隊的小朋友分成兩隊,並且為了讓他們能夠認識更多新朋友,於是希望儘量把互相不認識的小朋友分在同一隊。這樣的問題可以被抽象描述成一個「最大切割(Max cut)」計算問題如下:將每個人對應到一個點(vertex),如果兩個人互相認識的話,則把相對應的兩個點連起來,並稱這條線為一個邊(edge)。最後的目標是要找到一個切割(cut),也就是將各個點標上0或1,並讓越多的邊橫跨0和1(如下圖(a))。具有最多橫跨0和1的邊的切割,又被稱為最大切割。
有沒有什麼演算法可以迅速的找到最大切割呢?很可惜的是,在經過數十年專家們的腦力激盪,仍然沒有什麼快速的演算法可以找到最大切割。甚至有些理論上的證據顯示最大切割問題真的很難(是個NP完備問題,相關概念在本章後段和下一章將會提到)。
不過幸運的是,雖然找到最大的切割很困難,不過如果我們退而求其次,只想要找到一個沒有比最大切割差太多的切割,那麼將會有許多快速的演算法!其中以下這個非常簡單的隨機演算法,將可以給我們一個切割,其橫跨0和1的邊數量至少是最大切割的50%。這個隨機演算法大概會是你看過最簡單的演算法了:將每個點有50%的機率設為0,50%的機率設為1(下圖(b))。為什麼這樣的演算法可以達到最大切割的50%呢?
讓我們先看一對相互認識的朋友,算一下有多少機率他們將會被分在不同隊。沒錯,如上圖(c)所示,他們將會有50%的機會被分在不同隊。現在,讓我們計算在“期望上”,有多少個邊(也就是一對認識的朋友)會被切割,也就是說當我們不斷重複這個隨機演算法,平均下來的切割數量會是多少。是的,因為切割數量就是把去加總被分在不同隊的邊個數,而且每個邊每次有50%的機會被切割,所以平均下來我們期望看到有一半的邊被切割!由於最大切割數量頂多就是邊的總數,所以我們總結這個隨機演算法在期望值上可以達到最大切割的50%。你想的出來其他更好的隨機演算法嗎?
Hash函數(Hash function): 想像你是一個旅館老闆,每天有大量的客人進進出出,你希望設置一個特殊的貼心服務,讓熟客們可以將他們的旅行用品直接寄放在旅館內,這樣就不用每次都佔用行李箱的空間了。這時候問題來了,該如何將儲物櫃分配給各個熟客呢?由於熟客的數量可能會變動,如果直接用姓名的ㄅㄆㄇ或ABC來做固定的排列,可能會造成過多的空格,或是某個字母太多人不夠用。有沒有什麼快速且方便的演算法幫你避開這些潛在的麻煩呢?
Hash函數(Hash function)的功能是將任意長度的0/1字串,對應到一個固定長度的0/1字串,並且具有一個特殊的性質:很難找到兩個不同的0/1字串被對應到相同的輸出0/1字串(這樣的Hash函數又被稱為免衝突的(collision-free)Hash函數)。一個最容易實作Hash函數的方式,就是直接讓它把每個0/1字串隨機地對應到一個輸出。
一旦有了一個Hash函數,我們就可以很輕鬆地解決上述的旅館儲物櫃問題了!現在我們可以將儲物櫃的編號對應到Hash函數的輸出空間,也就是說如果Hash函數的輸出是長度為5的0/1字串,那麼我們會將$2^5=32$個儲物櫃編號為00000,00001,00010,…,11111。而當一位客人正式成為熟客,要加入儲物櫃服務時,我們只要將他的名字輸入Hash函數中,並用相對應的輸出作為其儲物櫃編號。根據Hash函數免衝突的性質,我們將可以確保熟客之間盡可能地會使用到不同的儲物櫃。
隨機行走(Random walk): 當第一次自助旅行來到一座城市,想要盡可能地探索每個角落,有什麼辦法可以增加去到一些意想不到的地方的機會呢?也許很多人會嘗試在每個路口,和旅伴猜拳決定要往哪邊前進,這樣隨機在一座城市行走的想法,竟然和許多有用的隨機演算法有異曲同工之妙!
想像你想要隨機的產生一張柴犬的照片,或是隨機的選一家好吃的餐廳。由於選擇實在太多了,我們不可能先把所有選項都看過一遍,然後在用公平的機率隨機挑一個。有沒有什麼辦法可以讓我們只要透過定義清楚什麼是我們感興趣的東西,然後就可以很快的在之中公平地隨機採樣(random)出一個呢?
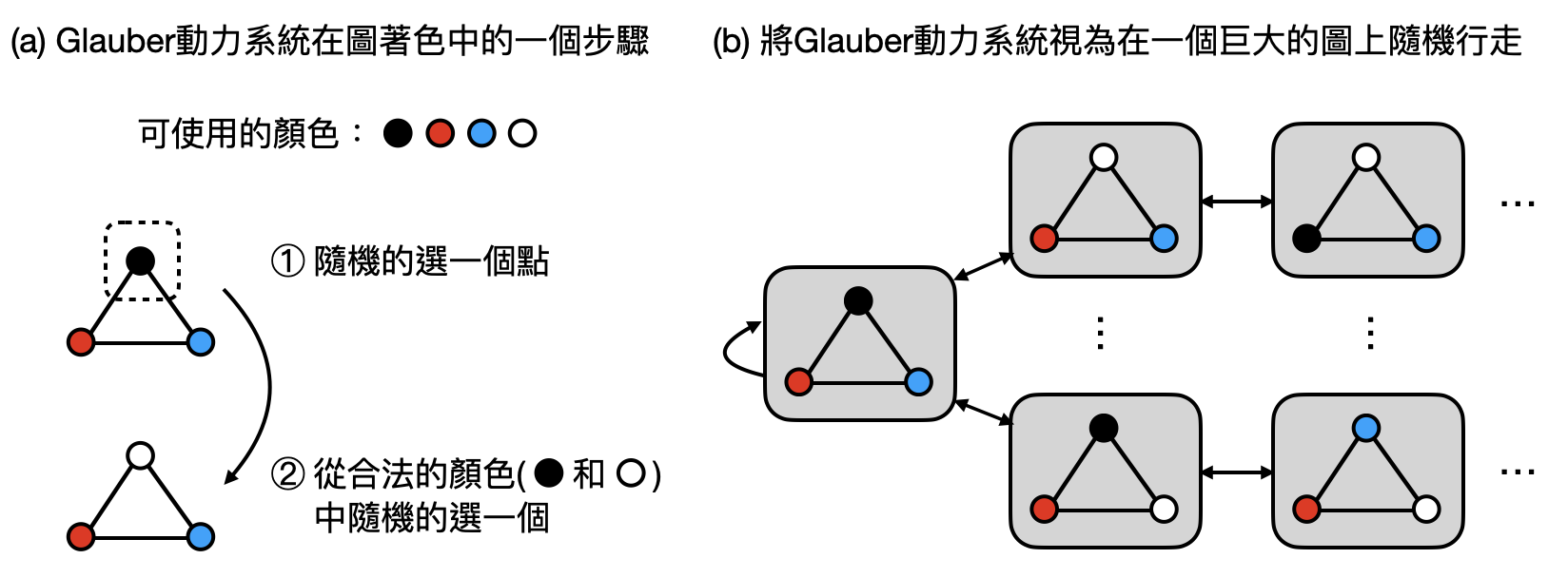
一個最常見的做法是「Markov鏈Monte Carlo方法(Markov Chain Monte Carlo, MCMC)」,在這邊讓我們直接從一個具體的例子開始:用Glauber動力系統(Glauber dynamics)來隨機地生成一個圖著色。首先,一個圖就是如同之前提到的由點和邊組成的數學物件,而一個合法的圖著色則是將每個點塗上顏色,並確保相連的兩點被塗上不同的顏色。假設現在我們想要從所有合法且使用6個顏色的圖著色中,隨機選出一個,要怎麼做呢?Glauber動力系統用了以下這個聰明的方法:首先從一個合法的圖著色開始,接著在每一步都先隨機選擇一個點,並且在確保著色合法的前提下,將其隨機地塗一個顏色(如上圖)。對很多圖來說,不需要經過太多步驟,Glauber動力系統就可以開始平均地隨機產生合法的圖著色了!
計算複雜度
在上一章,我們看到Turing證明了停機問題是不可解的。也就是說,不存在一個演算法可以在有限時間內解決停機問題。在本章中,目前為止我們看到了各式各樣的演算法、計算模型、計算資源等等,從可解性的角度上來看,它們基本上是等價的(除了在“一致性(uniformity)”上有些關於數學中有限與無限的糾結處要講清楚)。然而在實務層面上,不同的演算法可能快慢很不一樣,同一個計算問題在不同計算模型下,也有可能被解地不一樣快。另外,不同計算資源之間也許可以有些取捨權衡。這些問題跨越了單單針對可解與否的探討,進入了研究「計算複雜度(Computational complexity)」的領域。
漸進分析
電腦科學家採用了「漸進分析(Asymptotic analysis)」,作為計算複雜度的數學根基。漸進分析的概念和動機很簡單:當計算問題的輸入很小的時候,所使用的資源基本上都很小,沒什麼好比較的。例如做個一位數的加法和乘法,基本上都是在幾秒內可以解決的事情。計算的複雜程度和所需的資源多寡,是當問題的輸入很大的時候才看得比較明顯,假如現在要計算的是十位數的加法和乘法,我們做加法的速度將明顯地比做乘法還要快多了。
上述的觀察,告訴我們與其針對特定的問題實例探討需要花費的相關計算資源等等,不如把使用的計算資源和相對應的問題輸入大小記錄在一個函數中,然後研究這個函數的成長性質。以在學校學到的加法和乘法的計算方法為例,如果現在有$n$位數的數字要相加,需要做的基本操作(在這邊指一位數的加減乘除)大約是$n$個這麼多。然而對於$n$位數的乘法來說,需要的基本操作則是大約需要$n^2$個。於是電腦科學家就把學校教的加法方法的(時間)計算複雜度函數訂為$n$,然後把學校教到的乘法方法的(時間)複雜度函數訂為$n^2$。我們可以看到當$n$很大的時候,$n^2$遠大於$n$,也就是說使用在學校學到的計算方法中,乘法遠比加法還要複雜。
也許有些讀者已經注意到了,為什麼在上一段的文字中,要一直繞口地強調“學校學到的加法/乘法”呢?這是因為計算複雜度函數在一個給定的演算法上,非常容易定義,直接計算所需的計算資源就好了。也就是說,上一段提到的$n$和$n^2$是某個加法演算法和某個乘法演算法的計算複雜度函數,而非加法和乘法這兩個計算問題的複雜度。
演算法的複雜度,被定義為"所需的計算資源"和"問題輸入大小"之間的函數。
那我們該如何定義計算問題的複雜度函數呢?
計算問題的複雜度,被定義為所有可以解決這個問題的演算法之中,複雜度最小的演算法的複雜度。
在這邊所提到的“計算資源”可以是任何一個你感興趣研究的計算資源,可以是時間,也可以是空間(記憶體大小),或是所需的隨機性等等。而根據不同的計算資源,我們稱呼相對應的複雜度為時間複雜度、空間複雜度、隨機性複雜度等等。
複雜度的近似與階層
一個演算法的複雜度,是和其所消耗的計算資源有關。然而,同樣的演算法根據不同的程式語言、機器語言、硬體設備等等,可以有許多不同的實現方式。也就是說,不同實現方式所消耗的計算資源會稍有不同。如此一來,我們到底該用那種實現方式的計算資源作為複雜度的定義呢?
沒錯,我們可以選擇使用圖靈機來定義演算法的複雜度!根據Church-Turing論題,我們相信任何的演算法實作方式都可以被一個等價的圖靈機描述,雖然所需的計算資源可能會稍有變化,但如此一來至少我們可以在數學上得到一個客觀的標準定義。但我們總不能每次要分析計算複雜度的時候,都把演算法寫成一台圖靈機吧!這可是所有資工系大學生的夢魘。但同時我們又希望計算複雜度既有個數學上面清楚的定義,又可以方便推導出來。
於是,為了方便電腦科學家們通常只會考慮「複雜度的近似(approximation)」。當你在大賣場逛街的時,在青菜區,也許你會非常注意每把5塊台幣和10塊台幣的差別。然而到了家電區的時候,你可能就不再會糾結於小於100塊台幣的差距。更進一步當你在買房子的時候,甚至連一、兩萬的差距都不在考慮之內了。也就是說,看到了18,599這個價碼,有些人可能會把它自動想成是18,600,有些人會想成是19,000,有些人可能更阿莎力地想成是20,000。這些都是對於原本的數字18,599的一個近似,可以讓我們更方便地感受到數字的大小,而不糾結於一些細微的差別。
對演算法來說,由於現在的電腦速度實在太快了,常常我們甚至感受不到時間複雜度$10n$和$100n$或和$n+1000$的差別。因此對於電腦科學家來說,時間複雜度$10n$和$100n$基本上是一樣的,它們都屬於同樣的「複雜度階層(order)」,並且被標記為$O(n)$。這裡的$O(\cdot)$又被稱為「大O符號」,在意思上就是要我們忽略$n$前面不同常數項的影響。
如此一來,通過關注不同的複雜度階層(利用大O符號做到),我們就可以省去討論不同實現方法的麻煩情況,更專注在演算法這個抽象的層次來討論計算問題的複雜度了!
多項式複雜度和指數複雜度
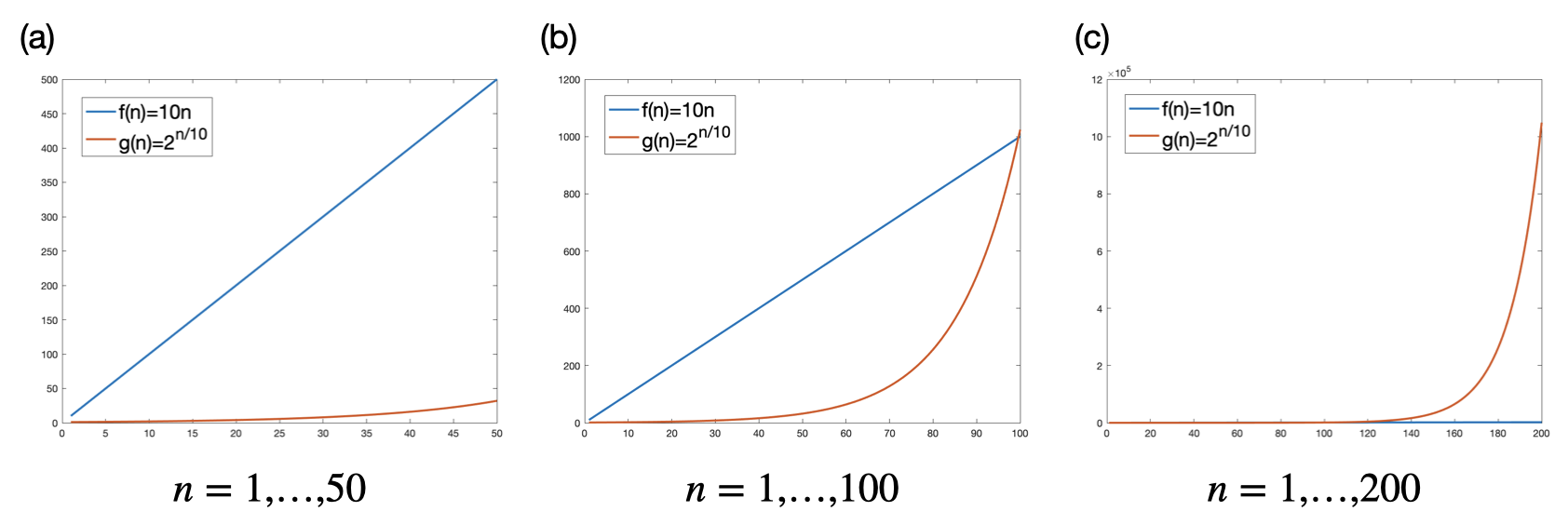
根據所使用的資源多寡,我們也可以更進一步區分出不同的計算複雜度類別。最常見的兩類就是所謂的「多項式(polynomial)複雜度」和「指數(exponential)複雜度」。在概念上,這和「摩爾定律(Moore’s law)」息息相關。摩爾定律是著名半導體公司Intel的合夥創辦人Gordon Moore(1929-2023)在1965提出的觀察:他猜想積體電路的每單位可以容納的電晶體數量,可以每兩年翻倍一次。翻譯成白話文來說,摩爾預測電腦的效能大約會是每兩年翻倍一次。也就是説在$N$年之後,電腦的效能會可能會是現在的$2^{N/2}$倍!而這樣的成長速率又被稱為指數成長(exponential growth)。
如果我們相信摩爾定律,那麼對於計算複雜度遠低於指數成長的計算問題,總有一天我們就會有夠快的電腦可以輕易解決。多項式複雜度就是其中一類這樣的計算問題,具體來說,如果一個複雜度函數$f(n)$,可以被證明有個常數$k>0$使得$f(n)=O(n^k)$,那麼我們就會說它的複雜度是多項式。常見的線性複雜度($O(n)$)和平方性複雜度($O(n^2)$)都是多項式複雜度的一種。
反之,對於複雜度為指數成長的計算問題,就算摩爾定律為真,我們可能還是無法用電腦快速地算出來!
計算複雜度類別
一旦我們可以對各個計算問題定義它們的計算複雜度,接下來我們就可以很自然地來將它們分類了!
讓我們先從最簡單的時間複雜度類別作為起點。對於一個函數$T:\N\to\N$,相對應的「時間複雜度類別」被定義為$\textsf{DTIME}(T(n))$,一個計算問題如果具有時間複雜度$O(T(n))$,就會在這個時間複雜度類別裡面(這裡$\textsf{DTIME}$的意思是「確定性時間(deterministic time)」,也就是說演算法沒有用到不確定性(non-determinism)和隨機性(randomness))。
$\textsf{DTIME}(T(n)) = $ {計算問題$L$:$L$的時間複雜度為$O(T(n))$}。
注意到,計算複雜度類別是個“集合”,搜集了所有擁有相似複雜度的計算問題。
同樣的,我們可以舉一反三用相同的方式對不同的計算資源和計算模型定義相關的計算複雜度類別。例如$\textsf{NTIME}$可以用來定義使用了不確定性的時間複雜度,$\textsf{BPTIME}$可以用來定義使用了隨機性的時間複雜度,$\textsf{DSPACE}$可以用來定義空間複雜度等等。
最後,根據複雜度函數為多項式成長或指數成長,我們可以更進一步只考慮幾類簡單的計算複雜度類別,以下是幾個常見的例子。
- $\textsf{P}$:多項式時間複雜度類。
- $\textsf{EXP}$:指數時間複雜度類。
- $\textsf{NP}$:多項式不確定性時間複雜度類。
- $\textsf{BPP}$:多項式隨機性時間複雜度類。
- $\textsf{NEXP}$:指數不確定性時間複雜度類。
- $\textsf{PSPACE}$:多項式空間複雜度類。
- $\textsf{EXPSPACE}$:指數空間複雜度類。
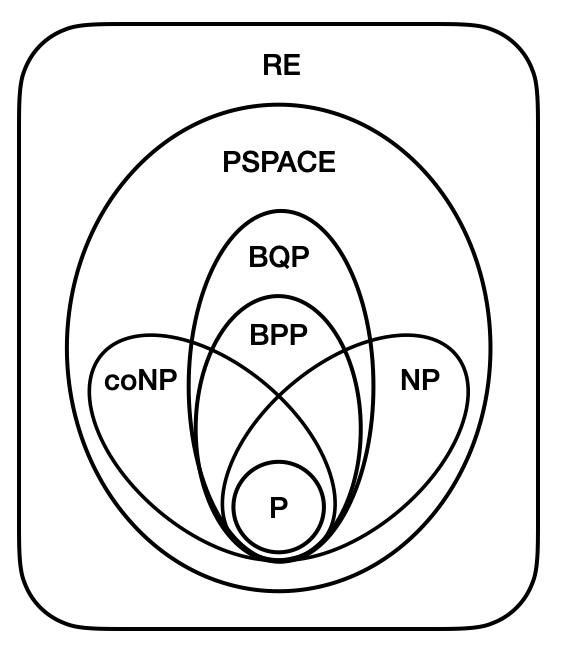
以上這些類別,包含了各式各樣常見的計算問題。由於多提供一些計算資源還是可以計算使用較少資源的問題,所以這些類別之間有著以下的包含關係($A\subseteq B$就是指$A$類別被完全包含在$B$類別中):
$\textsf{P}\subseteq\textsf{NP}\subseteq\textsf{PSPACE}\subseteq\textsf{EXP}\subseteq\textsf{NEXP}\subseteq\textsf{EXPSPACE}$
在這些包含關係中,我們目前只知道$\textsf{P}\neq\textsf{EXP}$、$\textsf{NP}\neq\textsf{NEXP}$和$\textsf{PSPACE}\neq\textsf{EXPSPACE}$,其他的包含關係(例如$\textsf{P}\subseteq\textsf{NP}$)我們還不知道是嚴格的包含(也就是說$\textsf{P}\neq\textsf{NP}$)還是等價的(也就是說$\textsf{P}=\textsf{NP}$)!
P vs. NP問題
在本章的最後,讓我們用理論電腦科學學界中最重要的聖杯問題來做結尾:P vs. NP問題。
這是牛津大學的克萊數學研究所(Clay Mathematics Institute)的千禧年七大數學問題(每解開一個將會獲得一百萬美金)中,唯一和電腦科學相關的問題。而在我們花了這麼多的篇幅建立圖靈機、非確定性、漸進分析和複雜度類別的概念之後,這個問題的數學定義就非常容易描述了:到底$\textsf{P}=\textsf{NP}$還是$\textsf{P}\neq\textsf{NP}$?
為什麼這個問題如此重要?為什麼這個問題困擾理論電腦科學家這麼多年?這個問題又和一般人的生活有什麼關係?
雖然我們是用數學的方式在問P vs. NP問題,不過根據之前提到非確定性計算和靈感之間的關聯,我們可以姑且將這個問題改寫成以下的日常生活版本:
P vs. NP問題的非正式版本:靈感與創意是否可以被機械化?
一個人能夠容易地品嚐出美食的優劣,是否代表也能夠輕易地創作出美食?一個人能夠迅速地鑑賞藝術品的價值,是否代表也能夠信手捻來一幅佳作?我們可以在各個其他的行業/領域中問出類似的問題,而在現在這個人工智慧突飛猛進的時代轉捩點,這些問題更是尖銳的要我們捫心自問,到底靈感、創意、天才是不是都可以被(確定性的)機械化的計算取代?(在之後關於機器學習和人工智慧的章節,我們會再更深入地做討論)
這樣對生活版P vs. NP問題的詮釋也許有點過於沈重,從數學的角度上來看,P vs. NP問題的解決與否以及最終答案為何,很大的機會上並不會對現實世界造成太大的影響。讓我們來開開腦洞,想像P vs. NP問題的兩種可能結果,各自會帶來什麼樣的影響。
首先,假如有人證明了$\textsf{P}\neq\textsf{NP}$,那麼這樣的結果可以說是符合預期、皆大歡喜。然而由於$\textsf{P}\neq\textsf{NP}$是個「最壞情況(worst-case)設定」的結果,其數學證明八九不離十會是用到了複雜的數學工程,其中討論到的計算問題和問題實例將會與實際可能會出現的差距甚多。
再來,假如是$\textsf{P}=\textsf{NP}$被證明出來了,那麼就代表找到了一個多項式時間的確定性演算法取代非確定性。乍聽之下非常可怕,如此一來許多密碼學系統將會被破壞(下一個章節中將會更深入介紹),幾年前Matt Ginsberg的一本小說『Factor Man』中,就使用了一個類似於$\textsf{P}=\textsf{NP}$的場景,想像世界會變得怎麼樣,是個空閑時可以輕鬆閱讀的小品。不過持著和上一段一樣的理由,如果真的有人證明了$\textsf{P}=\textsf{NP}$,我敢打賭這樣的演算法將只會是一個數學藝術品,無法在現實世界中實現。
也許,P vs. NP問題既是個理論世界中的聖泉,滋養並孕育出抽象境界的鬼斧神工,也是個現實世界中的隱喻,叩問我們踩在自由意識邊界的哪一邊。
總結
在本章中,我們看到了許多演算法的例子、兩種不同的計算模型、以及兩種常見的計算資源。從之中,我們可以感受到圖靈機的數學架構替分析和討論帶來很大的便利性。相對應之下,我們使用了漸進分析以及階層近似,關注計算資源隨著問題輸入大小成長時的變化為多項式還是指數。如此一來複雜度類別的概念很自然地浮現,開啟了計算複雜度理論的大門。
在下一章,我們首先會學到近代理論電腦科學最重要的工具:歸約方法(reduction method),然後承接本章走入計算複雜度理論之門,看看如何將許多對計算不同面向的討論,轉化為具體的數學形式,並發現一些出乎意料的關聯。最後,我們將從歷史發展的縱深來認識當今火紅的機器學習與人工智慧。
延伸閱讀
教科書與其他教材:
- S. Arora and B. Barak. Computational complexity: a modern approach. Cambridge University Press, 2009.
- A. Wigderson. Mathematics and computation: A theory revolutionizing technology and science. Princeton University Press, 2019.
科普書籍或小說:
- L. Fortnow. The Golden Ticket: P, NP, and the Search for the Impossible. Princeton University Press, 2013.
- M. Ginsberg. Factor Man. Zowie Press, 2018.