$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



第3章

歸約方法與近代發展





Every new body of discovery is mathematical in form, because there is no other guidance we can have.

所有新的發現都是以數學的形式出現的，因為我們並沒有其他引路的明燈。

Charles Darwin

目前為止，我們看到了各式各樣的演算法、計算模型和計算資源，並透過計算複雜度比較它們之間錯綜複雜的關係。例如身為七大千禧年數學問題的“P vs. NP”問題，就是在詢問“非確定性”是否可以替一般的計算模型帶來巨大的加速。在本章中，我們將延續之前打下的根基，進一步學習理論電腦科學的核心技術：「歸約方法(reduction method)」，並從五花八門的具體例子中熟悉如何從歸約的角度思考。最後，我們將簡單一瞥電腦科學在近年來最迅速成長的子領域：機器學習與人工智慧，從歷史與理論的縱深省思現況和展望未來。

歸約方法

在路上隨便攔一個人，問他加法和乘法哪個比較簡單，相信大部分人都會說加法比較簡單。如果你也這麼覺得的話，可不可以試著解釋一下為什麼覺得加法比乘法簡單呢？尤其是，為什麼你可以用比較快的速度算出加法呢？

最直覺的方法可能是拿出以前學過如何計算加法和乘法的方法，然後比較它們所需的計算步驟。這樣子的確就可以很明顯看出來，計算兩個$n$位數的加法只需要$O(n)$個計算步驟，然而學校裡通常學到的乘法卻要用到$\Omega(n^2)$的計算步驟。所以在固定所使用演算法的情況之下，我們的確可以很容易地比較不同計算問題之間的難易程度。

但如果現在我們考慮的是“任意”的演算法呢？我們該如何排除存在更快乘法演算法的可能性呢？事實上，兩個$n$位數的乘法其實有個$O(n\log n)$時間的演算法！不過雖然如此，人們目前還是無法排除存在一個$O(n)$時間的乘法演算法。說到底，要在數學上證明“不存在複雜度小於XXX的演算法”是個極度困難的事情。想像一下，這就像是要你證明人類跑百米不可能比現在的世界紀錄(博爾特(Usain Bolt)在2009年締造的9.58秒)還快一樣！雖然總覺得應該不可能再更快了，但還是無法排除未來出現一個新的賽跑天才(或是新的乘法演算法)的可能性！

這樣聽起來好像有一點喪氣，如果“證明計算問題沒有更有效率的演算法”是個這麼困難的數學問題，那麼理論電腦科學家到底在研究些什麼呢？有沒有什麼辦法可以讓我們能“間接地”理解一個計算問題的複雜度呢？

從“比較簡單”到“沒有比較難”

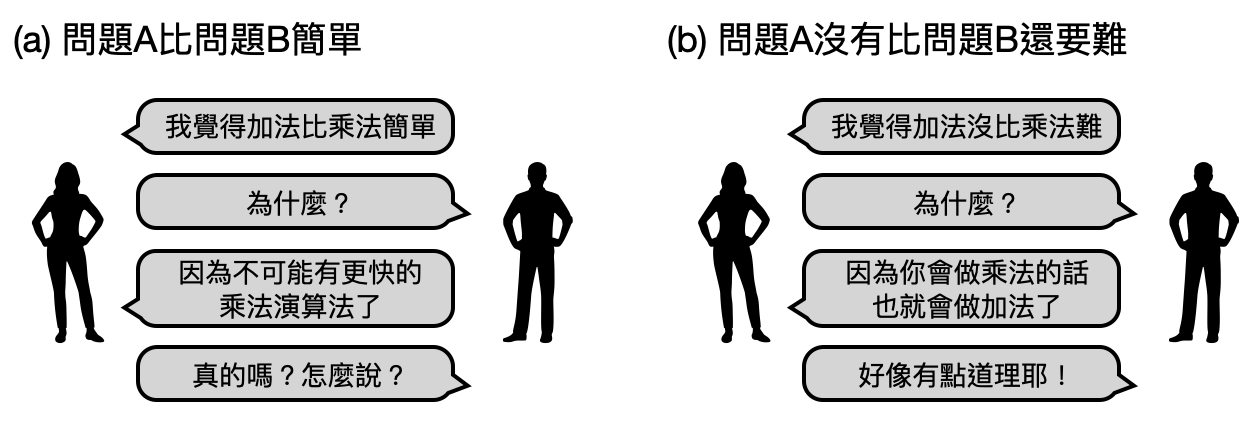
從之前的討論，我們發現如果想要證明問題A比問題B還簡單的話(如下圖(a))，需要排除掉問題B存在一個快速演算法的可能性。“排除掉任何快速演算法”造成了數學上的困難，如果我們考慮另外一個方向：“證明問題A沒有比問題B還要難”，會不會在數學上比較容易處理呢？

首先，什麼叫做“問題A沒有比問題B還要難”(如下圖(b))？直覺上，一個很合理的定義可以是，如果問題B有個快速的演算法，那麼問題A也會有個快速的演算法。也就是說，一旦問題B是簡單的，那麼問題A也會是簡單的，所以問題A沒有比問題B還要難！

從想要證明“比較簡單”到“沒有比較難”，有讓事情變得比較容易嗎？有的！注意到現在我們不再需要去“排除”任何神秘演算法的存在，我們反而是先假想如果有個問題B的演算法，該如何幫問題A設計一個複雜度差不多的演算法！這樣探討計算問題之間複雜度關係的方法，又被稱為歸約方法(reduction method)，是計算理論中最核心的數學技術。

如果「問題B有個快速的演算法」代表「問題A也會有個快速的演算法」，那代表問題A可以被(快速地)歸約到問題B。符號上計為問題A$\leq_p$問題B。其中下標p指的是多項式時間。

該如何證明問題A可以被歸約到問題B呢？有兩個常見的方法：Karp歸約法(Karp reductions)和Turing歸約法(Turing reductions)。

Karp歸約法

Richard Karp是位理論電腦科學領域的先驅，生於雙親皆為哈佛大學校友的家庭，Karp也在哈佛大學完成了學士、碩士、及博士的學位。雖然帳面上看起來Karp拿的是應用數學的學位，在那個電腦科學還尚未完全自立門戶的年代，Karp在時代的浪潮之下成為了領域的先行者。

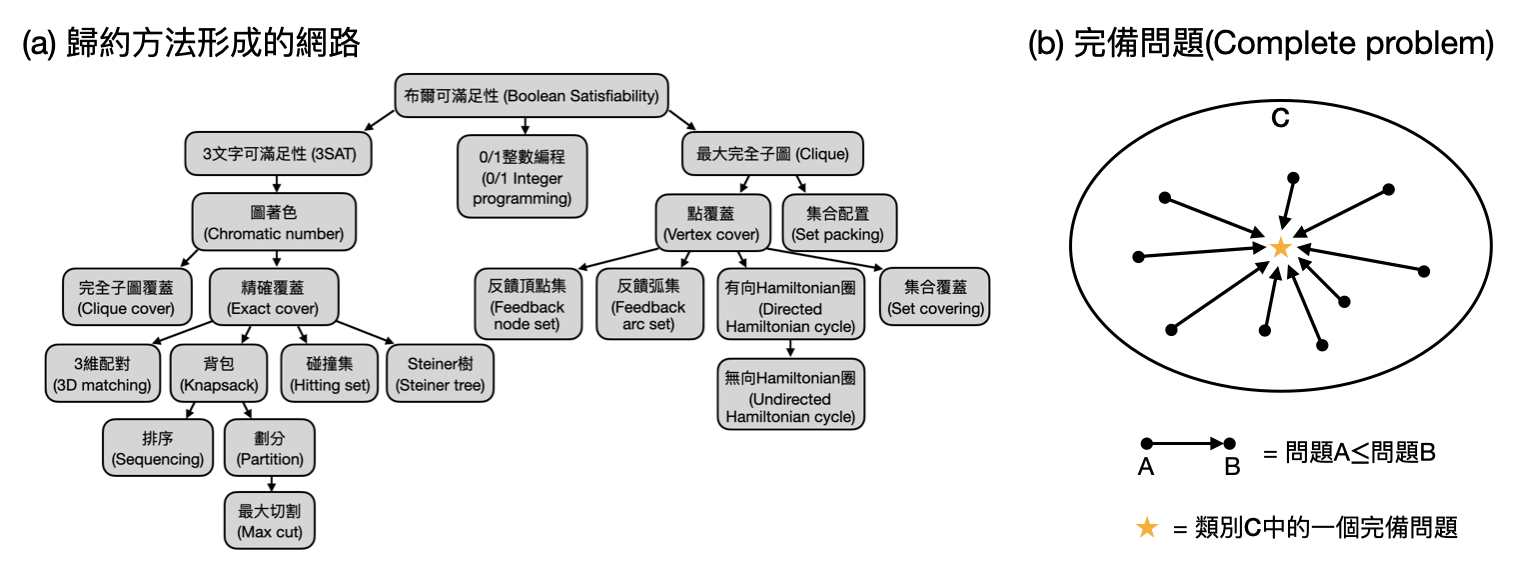
在1972年，Karp發表了篇可以說是理論電腦科學界中最重要的論文之一：「Reducibility Among Combinatorial Problems(組合問題之間的歸約關係)」。在之中Karp證明了21個組合問題是所謂NP完備問題(NP complete problems)，也就是說，所有NP內的問題都可以在多項式時間內歸約到這些問題(在本章後段將更深入探討完備問題是什麼)。而在這篇論文中，Karp精湛地使用各種數學巧思，設計出五花八門的歸約手法。這些歸約方法的共通點則是，它們都是將一個問題A的問題實例，有效率地(在多項式時間內)轉換成問題B的一些問題實例，並且保證如果能將問題B的這些問題實例解出來的話，就可以得知原本問題A的問題實例的答案！為了紀念Karp的貢獻，人們於是將這一類的歸約技巧稱為Karp歸約法(Karp reductions)。

Karp歸約法：將問題A的問題實例有效率地轉換成問題B的問題實例。

讓我們用以下的例子來實際感受一下Karp歸約法。

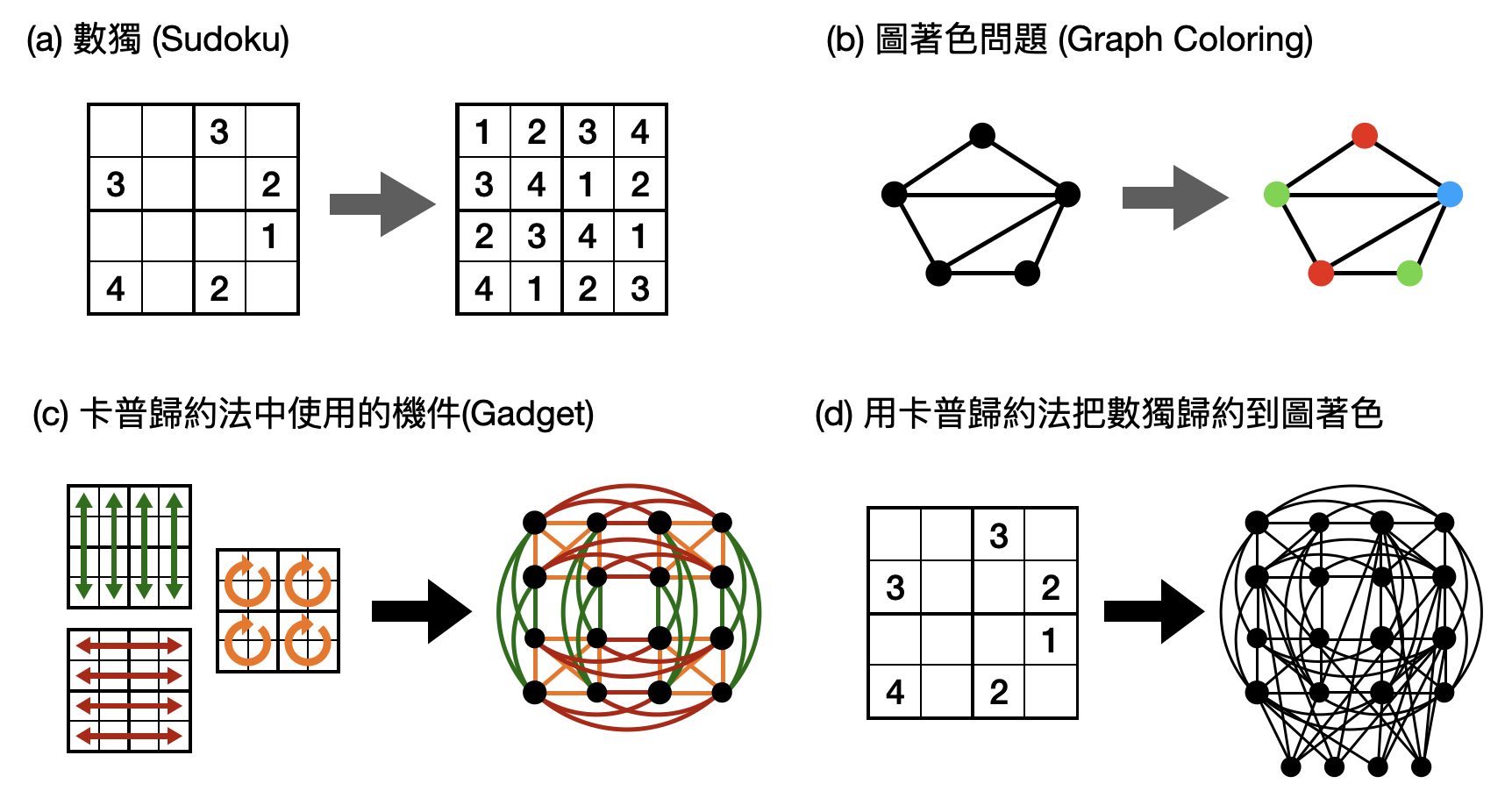
考慮問題A為老少咸宜的數獨(sudoku)問題，在下圖中為了方便我們使用4*4而非常見的9*9版本。在數獨問題中，我們要在方格裡填入1到4之間的數字，並保證每一行、每一列、以及每一個2*2區域內都沒有重複的數字(如下圖(a))。

問題B則讓我們考慮理論電腦科學中常見的圖著色(graph coloring)問題：問題輸入是一堆使用線條(edge)相連的點(vertex)，以及一個數字告訴你可以用幾種不同的顏色。一個合法的圖著色需要將每個點塗上顏色，並且確保被線條相連的點沒有被塗到一樣的顏色。例如在下圖(b)中，我們可以用三個顏色找到一個合法的圖著色，但無論如何都沒辦法只用兩個顏色達成合法的圖著色。

現在，我們想透過Karp歸約法把數獨的一個問題實例，轉換成圖著色的問題實例。首先，把每個方格字都轉換成一個點，並且假想點的顏色對應到了方格被填的數字。接著，每一行、每一列、以及每一個2*2區域對應的數字限制條件，可以轉換成不同的線條，變成為顏色需要不同的條件。以下圖(c)為例，2*2區域給的數字限制條件被對應到了橘色的線條。這些不同顏色的線條，對應到了原本數獨問題中不同的限制條件，術語上又稱為歸約法中使用到的機件(gadget)。最後，針對一個具體的數獨問題實例，我們可以透過之前提到的機件，將其轉換成一個圖著色的問題實例。例如在下圖(d)中，我們再額外多加了四個點(在最下方)，分別潛在的代表了四個不同的數字(由左到右潛在的代表1到4)，並且把已經有數字的方格對應到的點，連到下方的一些點上。例如左下角的方格已經填了4，

那麼我們就需要把相對應的點連到下方四個點中的前三個，來確保不能將其著色成4對應到的顏色。

Turing歸約法和神諭

Karp歸約法的核心精神在於轉換不同計算問題的問題實例，有如將問題揉來揉去改變形狀一樣。在某些類型的計算問題中(例如Karp研究的組合學問題)，這樣的歸約技巧可以很符合直覺、很好操作。但在一些情況，要把問題實例精準地轉換過去可能會變得太過複雜。同時，如果往後退一步重新思考歸約法的本質，會發現我們只需要能夠使用問題B的演算法來解決問題A就好了。也就是說，我們可以把問題B的演算法看成一個如同「神諭(oracle)」一般的存在，假想這個神諭可以正確地幫我們解決問題B，我們可以拿它作為幫手來設計問題A的演算法嗎？這樣的歸約方法又被稱為Turing歸約法(Turing reductions)。(注意到Karp歸約法是Turing歸約法的一個特例！)

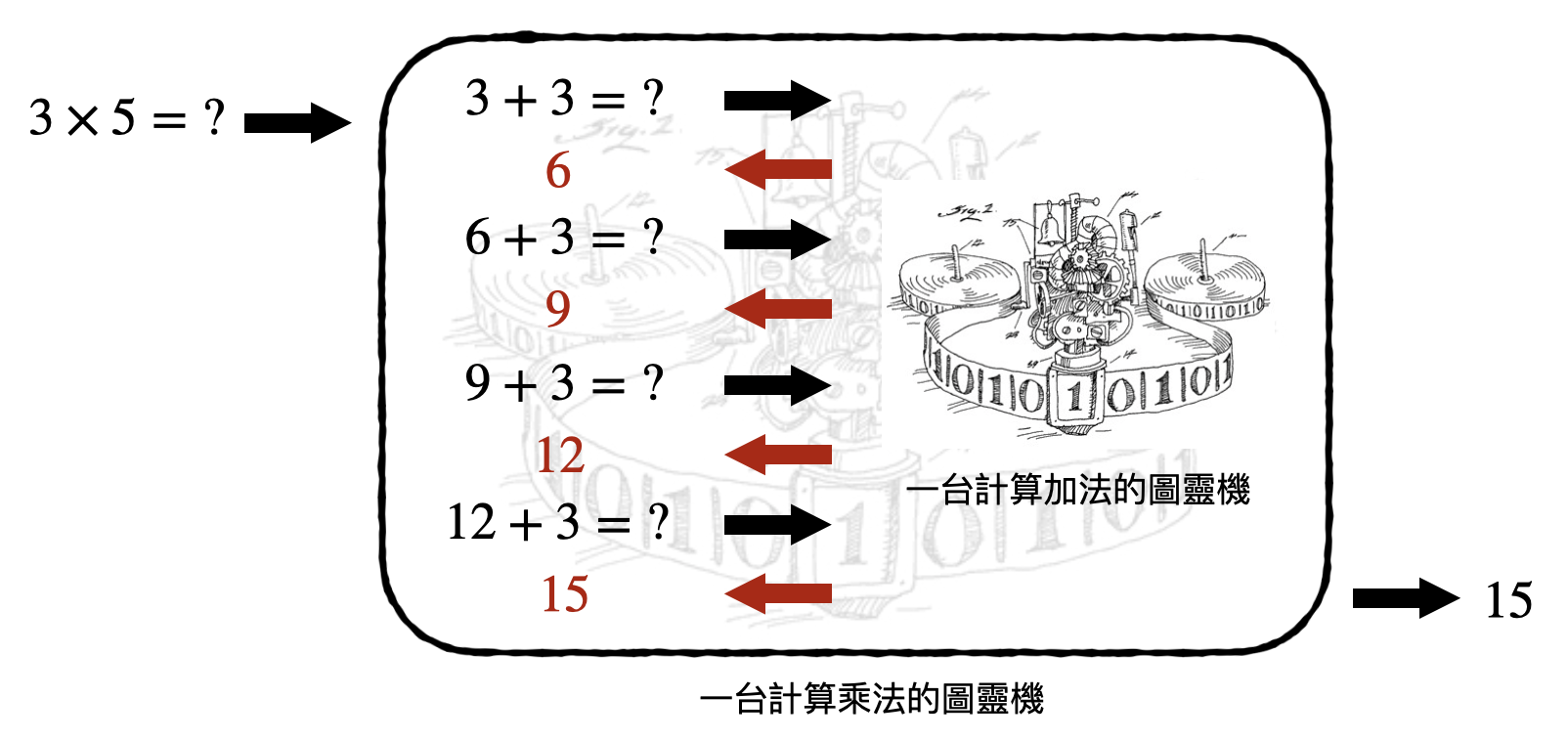
讓我們用一個非常蠢的例子來感受一下Turing歸約法和神諭：該如何將(整數)乘法歸約到(整數)加法呢？

想像你現在只能使用加法(和檢查兩個數字是否相同)來做計算，可以如何計算乘法呢？在計算$a\times b$時，一個最簡單粗暴的方式就是把$b$加了$a$次(或是把$a$加了$b$次)，如此一來只要不斷把現有的數字，使用計算加法的神諭把它和$b$相加，直到總共加了$a$次，就可以得到$a\times b$的答案了。如此一來，我們就用Turing歸約法將乘法歸約到加法了！(不過這邊其實還有個小小的技術點：該如何在演算法中確保我們剛剛好加了$a$次呢？是不是也可以利用加法的神諭(和檢查兩個數字是否相同的神諭)來確認呢？)

「神諭」這個名稱乍聽之下好像很玄妙複雜，不過其實概念上就只是將一個問題的演算法當成一個黑盒子，不去管這個黑盒子所需要用到的計算資源有多少。這樣就可以專注在如何將這個黑盒子當成一個小工具來使用。如此「模組化」的思考方式，在其他電腦科學的子領域也非常普遍！

完備問題

介紹完兩類常見的歸約手法後，希望讓讀者對於歸約方法的概念有些感覺了。在幾個段落之前，我們提到歸約方法主要的貢獻是在於可以說明「問題A沒有比問題B還要難」。因此，我們可以透過歸約方法將許多困難的計算問題串聯在一起，雖然無法直接證明它們無法擁有快速的演算法(如同前面說的，要排除任意的多項式演算法太難了)，但是歸約法可以告訴我們，這些被串在一起的計算問題，要嘛全部都很難，要嘛全部都很簡單！

(a)歸約方法可以將數個計算問題串成一個網絡。圖中的計算問題又被稱為Karp的21個問題，是最早一批被Karp證明為NP完備的計算問題。(b)一個複雜度類別C中的完備問題會被C中所有的問題歸約到。

挑一個你最喜歡的計算複雜度類別$C$(如果沒有特別喜歡的話，就選$\textsf{NP}$吧)，假設你可以在其中找到一個計算問題$L$，並且把$C$裡面所有的計算問題都歸約到問題$L$，那麼這代表了什麼？沒錯，這代表如果有個快速的演算法計算$L$的話，就可以對複雜度類別$C$裡任何的計算問題設計出快速的演算法！對於這樣的計算問題$L$，我們又將其稱為$C$的完備問題(complete problem)。在直覺上，一個複雜度類別$C$的完備問題，就是$C$裡面最難的問題之一。

完備問題存在嗎？該如何證明一個計算問題是某個計算類別的完備問題？

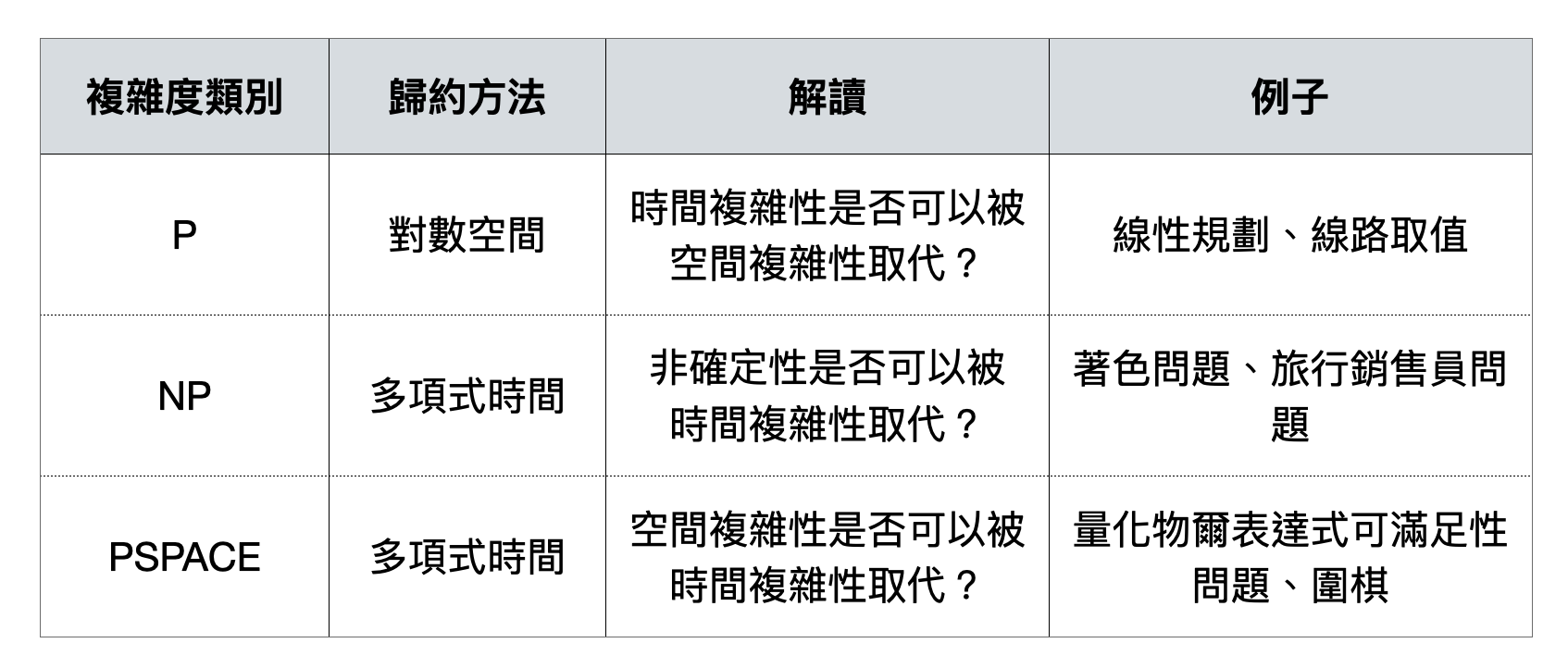
在定義完備問題時，歸約方法使用到的計算資源量也需要被仔細考慮。以複雜度類別$\textsf{P}$(包含了所有多項式時間內可以被解的計算問題)為例，如果我們讓歸約的過程也可以使用多項式時間的話，那麼就會得到一個不太有意思的結論：所有$\textsf{P}$裡面的計算問題都是$\textsf{P}$的完備問題。於是理論電腦科學家在定義$\textsf{P}$的完備性時，一般會限制歸約的過程只能使用「對數空間(logarithmic space)」。換句話說，這個定義下的$\textsf{P}$完備性刻畫的是$\textsf{P}$和空間複雜度類別$\textsf{L}$(包含了所有對數空間可解的計算問題)的差距。

NP完備性和Cook-Levin定理

關於完備問題最重要的課題就是NP完備性(NP-completeness)。顧名思義，一個計算問題$L$具有NP完備性，代表$L$是個NP的完備問題。由於多數的專家學者都相信$\textsf{P}\neq\textsf{NP}$，一個NP完備的計算問題可以被解讀為大家相信是困難的問題。除了用對於$\textsf{P}\neq\textsf{NP}$的信念來為NP完備性的困難度背書之外，另一個讓理論電腦科學家對NP完備性如此著迷的原因是在於，有大量在實務上困難的計算問題，都被證明具有NP完備性！

俗話說英雄所見略同，在二戰後到蘇聯解體(1991)之間的科學史大概就是最好的見證了吧！在理論電腦科學的初期發展階段，也有許多這樣有趣的例子，其中最出名的莫過於Stephen Cook和Leonid Levin在70年代初期不約而同發現第一個NP完備問題的事蹟。雖然兩人的切入角度略有不同，甚至因此有些學者傾向將貢獻只歸於Cook，不過大部分人還是將這項重要的里程碑稱為Cook-Levin定理(Cook-Levin theorem)。

Cook-Levin定理：所有NP裡的問題都可以在多項式時間內被歸約到布爾可滿足性問題(Boolean satisfiability problem)。由於布爾可滿足性問題在NP之內，因此布爾可滿足性問題是NP完備的。

Cook-Levin定理本身就像是個NP問題：從定理的敘述中感覺它很難，然而一看完證明後就豁然開朗，會覺得“不過就如此呀”。但隨著對計算有更多的接觸和思考後，Cook-Levin定理將會帶來越來越多的深刻體悟。從歷史的角度說起，Cook-Levin定理發現了第一個NP完備的計算問題，從此打開近代理論電腦科學的大門。不過，要證明一個計算問題$L$是NP完備需要將$\textsf{NP}$中“所有”的計算問題都歸約到$L$，到底該如何一次歸約複雜度類別中所有的計算問題呢？

這時候，圖靈機在數學定義上的方便性就派上用場了。如果對圖靈機地印象有點模糊，請回到之前相關的章節簡單複習一下！

使用布爾式來檢查圖靈機做計算的步驟：當圖靈機在做計算的時候，每一個步驟都只會更改到紙帶上位於指針附近的格子。因此，就算具有了非確定性，我們依然可以透過使用「布爾式(Boolean formula)」來偵測目前圖靈機正在使用哪個步驟，以及該步驟有沒有正確地照著規則做。舉個非常簡單但暫時和圖靈機無關的例子：假設現在有三個布爾變數$x,y,z$，而且有兩種可能性是可以接受的結果，(i)當$x=0$時，如果$y=z$；(ii)當$x=1$時，如果$y=\neg z$(這邊$\neg z$指的是將$z$的變數由1變成0或由0變成1)。我們可以透過以下兩個的布爾式來分別檢查變數們有沒有符合規則：

\begin{equation*} \phi_1:\ (\neg x)\wedge(y=z) \end{equation*} \begin{equation*} \phi_2:\ x\wedge(y=\neg z) \end{equation*} 這邊$\wedge$指的是布爾的「和(and)」，也就是說$x\wedge y$的值只有在當$x=y=1$的時候才會是1。另一個相關的符號是$\vee$，代表了布爾的「或(or)」，也就是只要$x$和$y$其中一個的值是1的時候，$x\vee y$就會是1。如此一來，我們就可以用$\phi_1\vee\phi_2$來表示只要這兩種可能性之一發生就好。

布爾可滿足性問題(Boolean satisfiability problem) 則是指以下的計算問題：輸入為很多個布爾式(例如上面提到的$\phi_1$和$\phi_2$)，問是否存在一種變數的取值使得所有布爾式都滿足(也就是值為1)。以上述的例子，$x=y=z=0$就是一個皆滿足$\phi_1$和$\phi_2$的取值方式，因此對應的布爾可滿足性問題是個對的(Yes)問題實例。

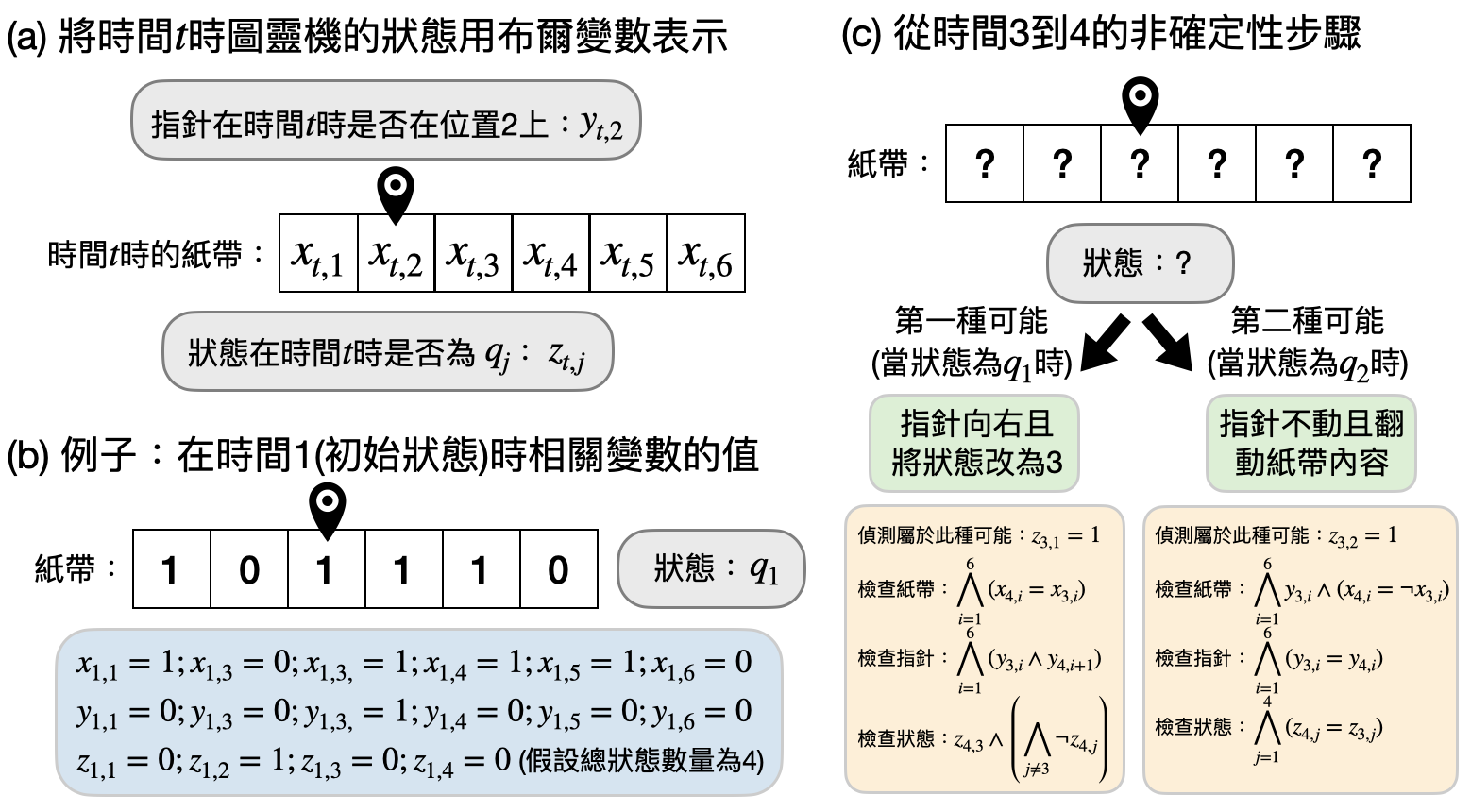
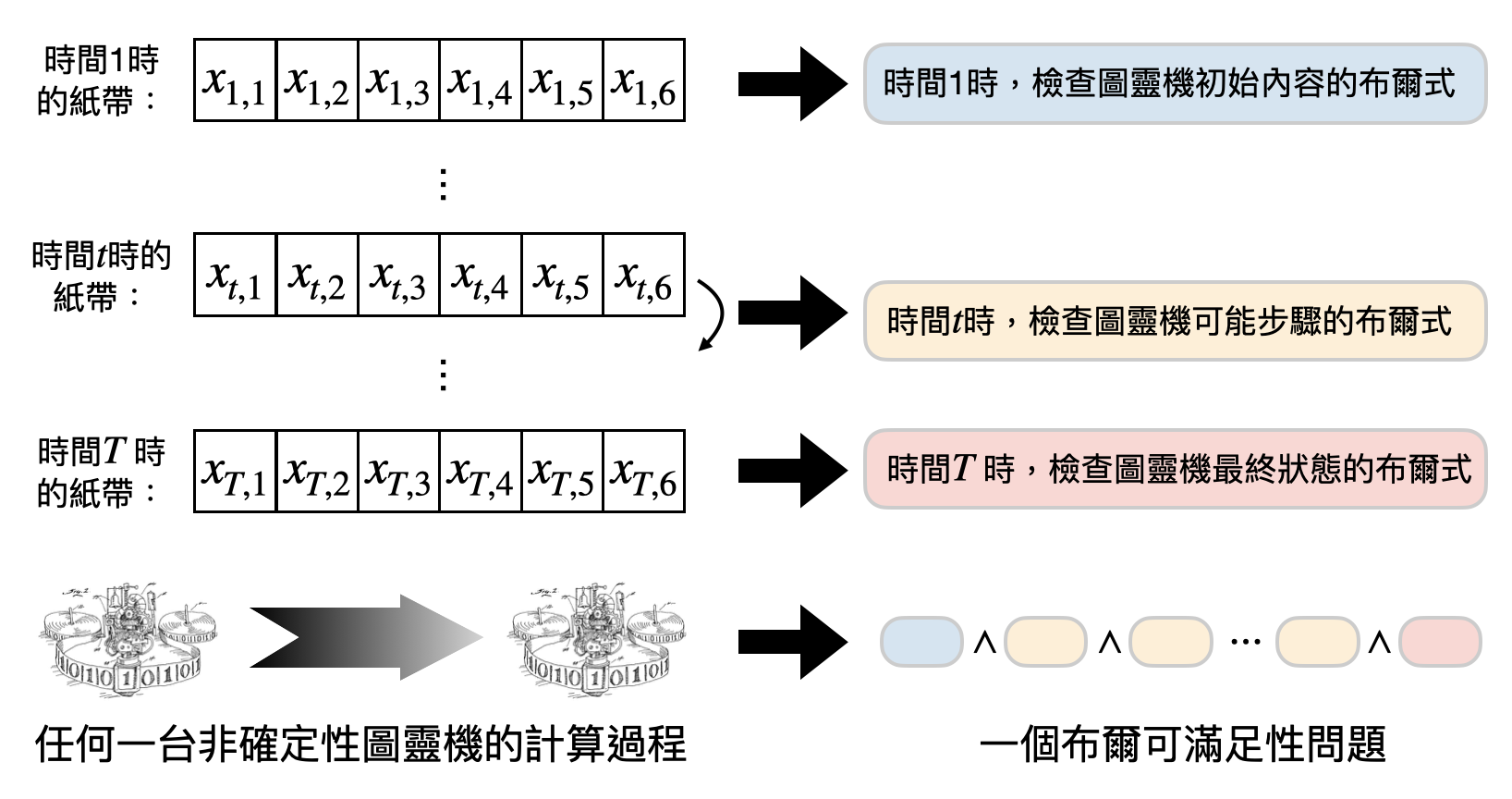
利用上述的概念，我們可以應用在圖靈機的非確定性步驟上，用布爾式來偵測和檢查一台圖靈機的每一個非確定性步驟是否合法。下圖解釋了基本的概念，為了讓圖能盡可能的清晰，有些細微的技術細節將會被省略，歡迎感興趣的讀者仔細思考看看圖中還缺少了什麼！

(a)首先將各個時間點t時圖靈機的紙帶內容、指針位置、和狀態用布爾變數(也就是0/1)來表示。(b)例如，在初始時間t=1時，例子中圖靈機的內容是如何對應到相關變數的值。(c)從每個時間點到下個時間點時(例子中用時間3到4)，可以純粹用變數來表示可能的轉換方法。最終的布爾可滿足性問題將會包含所有橘色的布爾式，下一張圖將會統整個步驟得到的布爾可滿足性問題。

Cook-Levin定理的重要性主要有兩點。首先如之前一再強調的，Cook-Levin定理找到了第一個NP完備的問題，打開近代理論電腦科學的大門。再來，Cook-Levin定理也是第一個將“動態的計算”和“靜態的計算”嚴謹地聯繫起來的數學證明。在這邊動態指的是像圖靈機在做計算時，會不斷地更改狀態、紙帶的內容、和指針的位置等等。而靜態指的是像布爾可滿足性問題，透過各個布爾式將計算刻入問題實例的輸入中。兩種計算方式的差別，就好比在中學數學考試時，有的人會從頭到尾推導公式來解題。有的人則是把所有可能會用到的公式背起來，現場帶入看看時答案是否正確。之後到了物理相關的章節後，我們將會看到更多Cook-Levin定理的影子。

Cook-Levin定理將任何一台非確定性圖靈機的計算過程問題(計算是否有一條計算路徑通往Yes的結束狀態)，歸約到一個布爾可滿足性問題。

至於為什麼之前提到的Karp的21個NP完備問題如此的重要？想像一下你身在電腦處於強褓中的年代，當時理論界中除了Turing的圖靈機和計算不完備定理之外，另外比較重要的就是Cook-Levin定理，說明了有一個計算問題是NP完備的。看到NP完備那樣奇特的數學定義，以及Cook-Levin定理中歸約出來的布爾滿足性問題，你可能會不自覺得猜想，也許並不會有那麼多NP完備的問題吧？要說明計算問題之間的難易關係看起來也太難了吧。這時候，你讀到了Karp的21個NP完備問題，看到21個新證據擺在眼前，你還會覺得證明完備性是個很困難的事情嗎？Karp就這樣開啟了計算複雜度理論的新頁。

近代理論電腦科學家研究的課題

圖靈機讓計算有了扎實的數學架構，Cook-Levin定理和Karp的21個NP完備問題聯手開啟了對於計算複雜度的比較與分類，理論電腦科學逐漸形成一個探索計算極限的學科。當電腦逐漸從想像變成實際，再變成日常生活不可或缺角色，理論電腦科學家們系統性地使用數學與邏輯的分析方法，先一步往後探尋計算在不同領域和應用中潛在的角色(例如密碼學、經濟學、物理學等等)，以及摸索不同計算模型與計算資源能夠達到的邊界。

在這一個小章節中，我們將從四個不同的角度：複雜度下界、偽隨機性、密碼學以及不同子領域之間的關聯來一窺近代理論電腦科學家探索的宇宙。

複雜度下界

在介紹歸約方法之前，我們提到如果想要證明一件事情A比另外一件事情B還要“簡單”，會需要解釋為何B無法有個簡單的解決辦法。由於“排除掉存在簡單解法”不是件容易的工作，於是理論電腦科學家才漸漸著重在使用歸約方法來證明事情A不會比事情B還要難。而我們也看到這樣的思路也的確成功地將許多困難的計算問題串聯成一個網絡(如某一張圖中Karp的21個NP完備問題)，一旦能夠證明其中一個完備問題是困難的，就等於證明所有的完備問題都是困難的！也就是說，如果能夠證明其中一個NP完備問題不在複雜度類別$\textsf{P}$裡面，那就等於證明了$\textsf{P}\neq\textsf{NP}$。

如此直接面對計算問題困難與否的研究課題，被稱為「複雜度下界(complexity lower bound)」，顧名思義就是要在沒有任何額外假設(unconditionally)的情況下，直接證明一個計算問題是困難的。這是不是一聽就很難呀！讓我們用個比較生活化的計算模型來舉個例子。

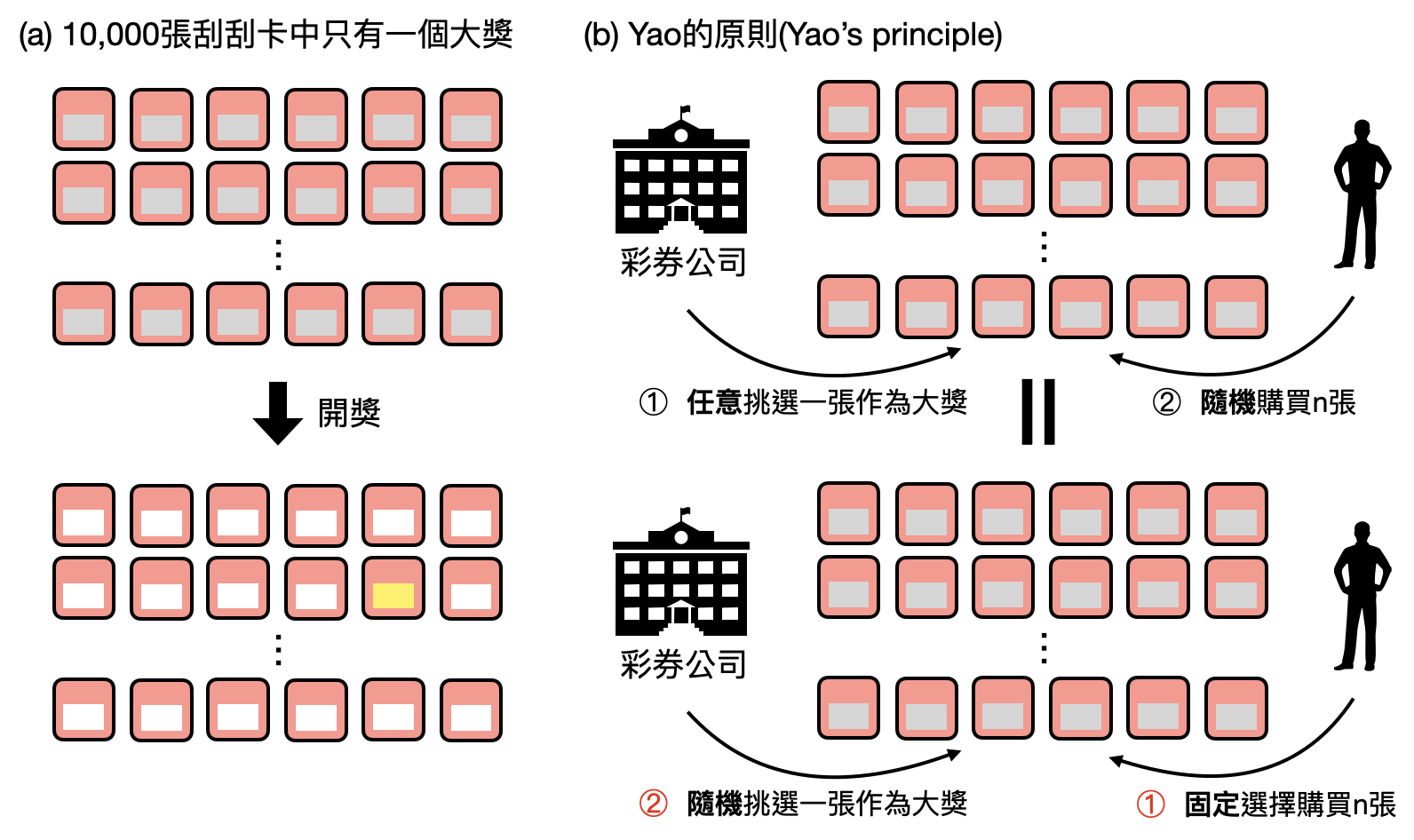
(a)數張刮刮卡中只有一張是大獎。必須要刮開(對應到計算理論中的“詢問”)才能看到是否中獎。(b)根據Yao的原則(Yao's principle)，一個隨機演算法的表現結果，將會等於一個確定性演算法對任何隨機輸入的表現結果。

農曆新年到了，你想要去買刮刮樂試試手氣。彩券行發行了10,000張刮刮卡，但只有一張是最大獎，如果想確保自己有很高的機率能夠刮中最大獎，那麼你大約需要刮幾張呢？沒錯，基本上要把這10,000張刮刮卡都試過才行！“需要刮幾張卡”在數學上會以「詢問複雜度(query complexity)」來描述。於是，說明清楚到底需要刮幾張卡才能有99%的機率刮中唯一的大獎，就是一個詢問複雜度下界的研究課題。下圖提供了一個圖像化的證明，這樣你還會想買刮刮樂嗎？

去除隨機性

在之前介紹各種計算模型和計算資源的章節中，我們看到了隨機性可以如何加快計算速度。然而，在歷史上有許多計算問題在擁有快速的隨機演算法(換句話說，這個計算問題被放進了多項式隨機性時間複雜度類$\textsf{BPP}$)沒過多久後，就被發現即使不使用隨機性，也可以被快速地解決(換句話說，這個計算問題被放進了$\textsf{P}$)。最經典的例子莫過於“質數判定問題”：上個世紀末，在演算法界其中一個重要的里程碑就是找到如何在多項式隨機時間內，判斷一個數字是否為質數。專家們一直無法取得共識是否能將演算法中的隨機性拿掉，直到2002年，兩位來自印度理工大學Kanpur分校的大學生Neeraj Kayal和Nitin Saxena，在修課期間挑戰了這個經典問題，最後和他們的老師Manindra Agrawal一起發表了論文『PRIMES is in P』，如標題所述將質數判定問題放入了$\textsf{P}$之中。

於是，一個很自然的問題就浮現了：隨機性真的可以為我們帶來本質上的加速嗎？或換句話說，具有隨機性的複雜度類別，是否等於相對應但沒有使用隨機性的複雜度類別？例如，$\textsf{BPP}$會不會其實等於$\textsf{P}$?這一類的研究課題，被稱為「去除隨機性(derandomization)」。

該如何思考隨機性在計算中扮演的角色呢？從演算法的角度來看，我們會在計算的步驟中不斷地擲一些骰子，並根據結果繼續做計算。這樣的過程，其實等價於我們先準備好許多骰子的結果，然後將這些結果用0/1的字串表示，並作為演算法的輸入。如此一來，我們把演算法中的隨機性全部轉移到輸入的部分，在計算的過程中就變成沒有隨機性了！

但當然，這樣還沒有完全將隨機性去除，不過上述將隨機性轉移到輸入的概念，已經可以提供一個大方向的思路來去除隨機性了：假設演算法需要使用到1000個骰子的結果作為隨機性，我們有沒有辦法自己另外產生一些長度為1000的0/1字串，讓使用它們作為演算法的輸入和使用真正的1000個骰子具有差不多的功效呢？最笨的做法，是將1000個骰子所有可能的結果都拿來作為演算法的輸入，然後再將結果取平均。不過如此一來，我們將需要執行演算法$2^{1000}$，這遠比宇宙的年齡還要大呢！有沒有辦法只選擇少量長度為1000的0/1字串，然後拿它們放入演算法後得到的結果取平均，作為一個好的估計呢？這種少量0/1字串的集合，又被稱為「碰撞集(hitting set)」(參考下圖(c)的例子)。

如果我們對所要去除隨機性的演算法一無所知，那麼不應該癡心妄想能夠靠這樣偷吃步成功。然而，如果現在我們知道這個演算法在做什麼，或是知道它是個處於比較低複雜度類別的演算法，那麼有沒有機會大幅降低需要拿來測試的0/1字串數量呢？

(a)計算三角形的最大切割。(b)之前的隨機演算法使用了三個隨機比特，等價於隨機選一個長度為三的0/1(黑/白)字串，並計算其相對應的切割值。(c)可以透過將第三個比個設為前兩個比特的XOR(也就是只有當兩者洽有一個是1的時候，第三個比特才會是1的)，或得相同的成效。由於現在只要使用兩個比特，總共只會對應到四個長度為三的0/1(黑/白)字串，這些字串組成的集合又被稱為一個碰撞集。

答案是，目前對於一些特定的演算法和比較弱的複雜度類別，理論電腦科學家們已經知道該如何產生還不錯的碰撞集，能夠在少量的確定性時間內產生0/1字串來取代隨機性，進而將演算法中的隨機性移除。不過對於是否能去除所有多項式時間隨機演算法(對應到複雜度類別$\textsf{BPP}$)中的隨機性，我們仍在努力中。在上圖中，我們將看到一個簡單的例子，展現如何將某個演算法中需要的三個骰子數量，降低到兩個！如此用兩個真正隨機的骰子產生出的三個結果，又被稱為「偽隨機(pseudorandomness)」。

密碼學

隨著電腦和資訊科技的普及，現代人幾乎人手一台智慧手機，並擁有各式各樣的網路帳號(從銀行到購物平台等等)。同時，每隔一陣子，就會在新聞上看到某某企業或政府機構的個資遭到駭客入侵而外洩，資訊安全的重要性也因此水漲船高。到底這些資安系統是如何讓駭客不容易破解？在沒有人為疏失的情況之下，我們如何建立對加密系統的信任？

這一切背後的藏鏡人，就是密碼學(Cryptography)。

在古代發生戰爭時，將軍們之間沒有網路通訊，而是需要依靠飛鴿傳書或是信使傳遞訊息，才能更有效率和安全地戰鬥。然而，飛鴿和信使都很有可能被敵人攔截，因此傳遞的書信內容勢必需要做一些加密，好讓敵人即使看到了內容也摸不著頭緒。

一個最簡單的做法是將每個字母/字符根據一個將軍們之間已經溝通好的方式做轉換，例如將A改為C，將U改為W等等。如此一來，在不知道轉換規則的情況之下，敵人看到的將是一堆亂碼。然而，這其實也不是個太好的加密方法，一旦敵人攔截了足夠多的信件，很有可能可以根據字母/字符出現的頻率，找出你們暗藏的轉換規則！像是英文字母中最常出現的是E，如果敵人在信件中發現K出現最多次，那麼很有可能你們的轉換規則就是將E轉為K。

如此“設計加密方法，然後被破解”這種貓捉老鼠的遊戲，是密碼學演進的常態。連當年電腦科學的祖師爺Turing，也是因為在二次世界大戰中英國對於加密系統的急迫需求，加速了電腦發展的進程。

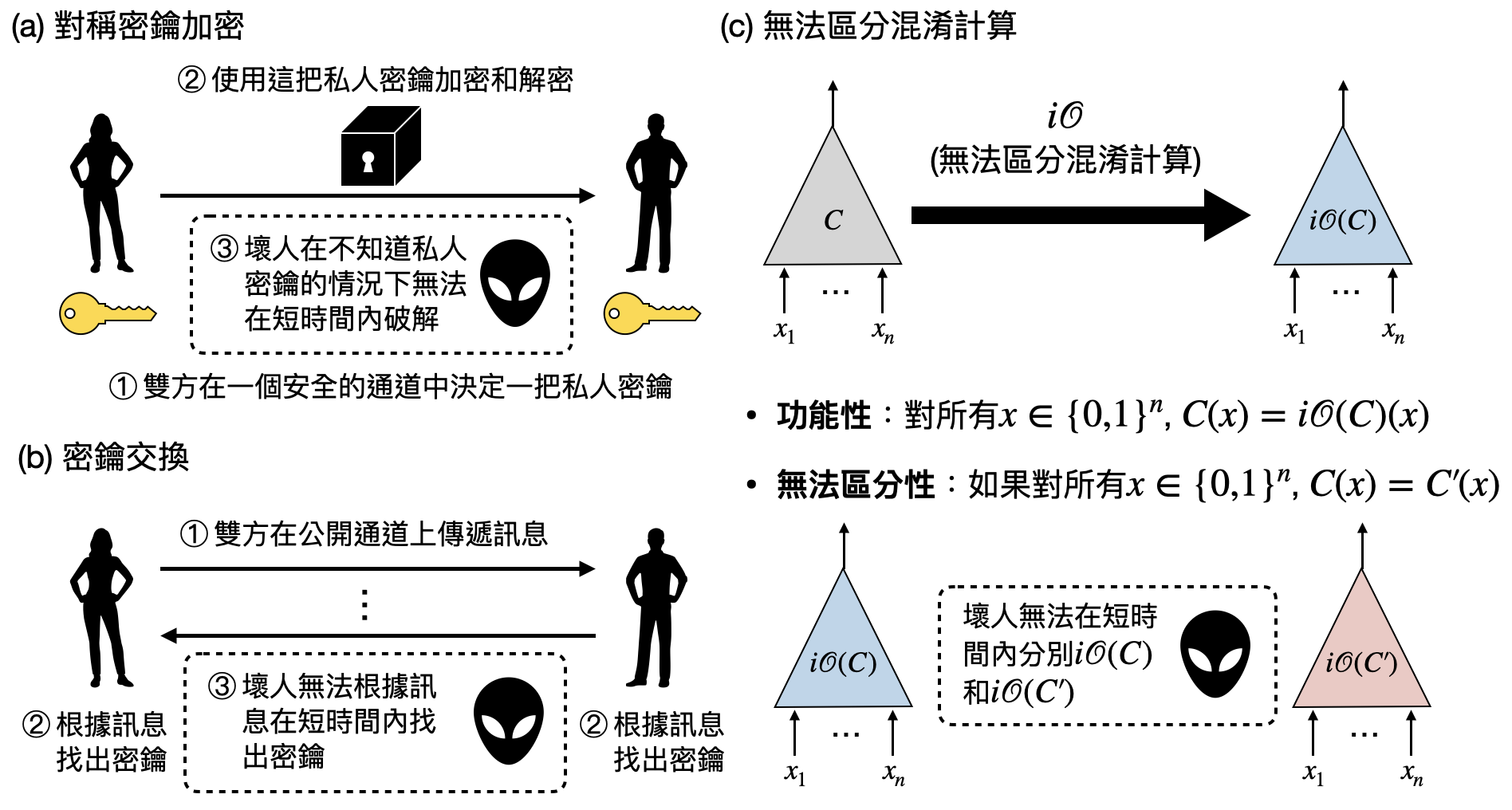
近代密碼學的發展，則是更進一步分工為許多部分，從如何設計有用的密碼基礎設施(cryptographic primitive)，到如何保證其安全性，然後接軌現實中的應用。以上述古代將軍傳信的例子來說，就是在替「對稱密鑰加密(Symmetric-key encryption)」這個密碼基礎設施設計一個安全的協議(參閱上圖(a)看看對稱密鑰加密的定義)。而現在的密碼學者，已經提出了五花八門的密碼基礎設施，例如「密鑰交換(Key exchange)」(上圖(b))問如何讓同一個陣營的將軍在只能透過飛鴿傳書的情況下，安全地產生一組共同擁有的密鑰(在數學上就是一個隨機的0/1字串)。有些密碼基礎設施在被研究多年後已經具有公認安全的協議，並在實際的情景中廣泛使用，例如用橢圓曲線(elliptic curve)做出的公鑰加密(public encryption)系統。有些則仍處於純理論階段，其安全性和實現能力都還在檢視當中，例如近年取得重大突破的「無法區分混淆計算(indistinguishability obfuscation)」(上圖(c))和「量子密碼學(quantum cryptography)」。

不同子領域之間的關聯

介紹完上面這幾個理論電腦科學的前端研究課題之後，乍看之下讀者可能會覺得它們各是不同的子領域，可能就這樣隨著時間的演進而漸行漸遠。不過在實際上，理論電腦科學中各派武功的路數其實常常可以融會貫通！透過歸約方法的角度，有大量的工作闡釋了不同子領域之間的關聯，以下讓我們品嚐幾個例子：

困難性與隨機性(Hardness vs. randomness)： 在前幾個段落中，我們認識了“複雜度下界”的目標是要找到一個複雜度很高的問題，以及“去除隨機性”的目標是將隨機演算法中的隨機性拿掉。從定義上兩者看起來沒什麼關聯，沒想到它們之間竟然有著緊密甚至接近等價的關係！

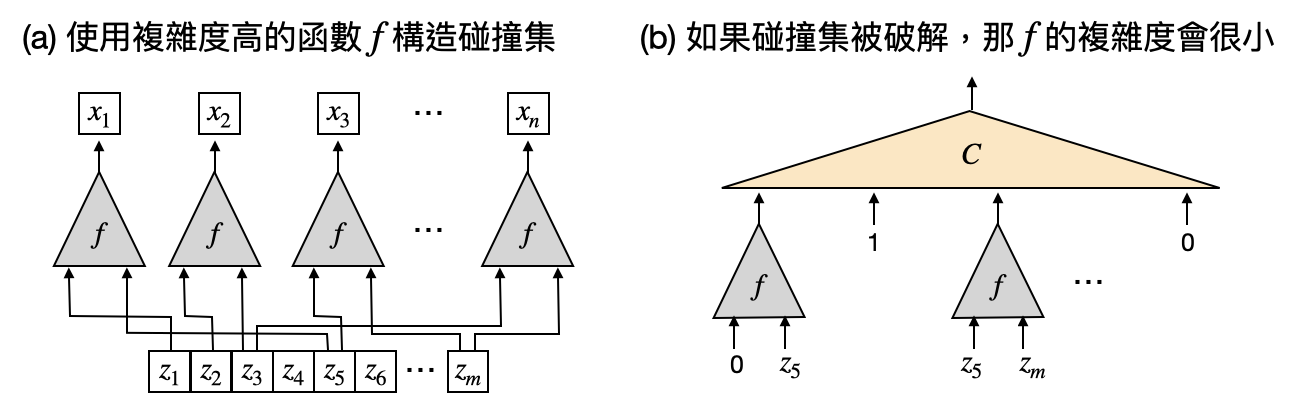
在這邊讓我們著重在其中一個方向：困難性如何取代隨機性。什麼是一個困難的計算問題呢？直覺上就是說看到了輸入後，很難立即知道輸出是什麼。換個角度想，這代表我們很難“預測”這個計算問題的輸出是什麼。同時，隨機性最大特色就是難以預測性。綜合以上兩個觀察，如果現在讓我們把一個困難計算問題的輸出作為隨機比特，會不會讓一個隨機演算法跑得很好呢！？下圖將會從“碰撞集”的角度將這邊抽象的想法轉化為實際的構造。

困難性與隨機性在計算中的等價，似乎也遙遙呼應著生活中的哲學：一旦能迎刃而解各種難事，生活中看似隨機混亂的鳥事，往回看似乎都早已命中注定。

(a)目標是要將隨機比特個數從n個降至m個。首先，將這m個比特(在圖中用z來表示)切出n個長度為k(大約是m開根號)的子集，並且確保它們兩兩之間只有很小的重疊。接著對於每個子集，都將相對應的z比特餵入f作為輸入，於是得到n個比特，這些就將是要來使用的偽隨機比特。(b)如果這樣的構造不是一個碰撞集，那麼代表有個小的線路C可以將其產生的偽隨機比特與真正隨機的比特做區分。接著，使用一些標準的證明手法，將可以把這個線路C轉換成一個小的線路來計算f，因此代表f的複雜度很小。如此一來，這和原本f複雜度很高的假設矛盾，於是這個構造應該是個好的碰撞集。

近代密碼學與計算複雜度： 在先前的段落中，我們看到密碼學家提出了各式各樣的密碼基礎設施，勾勒出資安世界的藍圖。除了功能性之外，這些密碼設施最重要的性質就是安全性(security)。例如在對稱密鑰加密中，我們希望第三方的“壞人(adversary)”沒辦法在看到密文後，短時間內破解其中的內容(這邊只要求短時間，是因為壞人總是能夠把所有可能的密鑰都試一遍，但這樣很花時間)。當提出一個密碼設施或是密碼構造(也就是針對某個密碼設施所設計出的一個具體實現方案)之後，該如何保證其安全性呢？

一個可能的方式就是看哪個密碼構造撐得比較久，還沒有被破解掉。就像是個貓捉老鼠的遊戲，構造密碼系統的人和破解的人相互軍備競賽，一來一回透過時間來證明某個密碼構造的安全性。

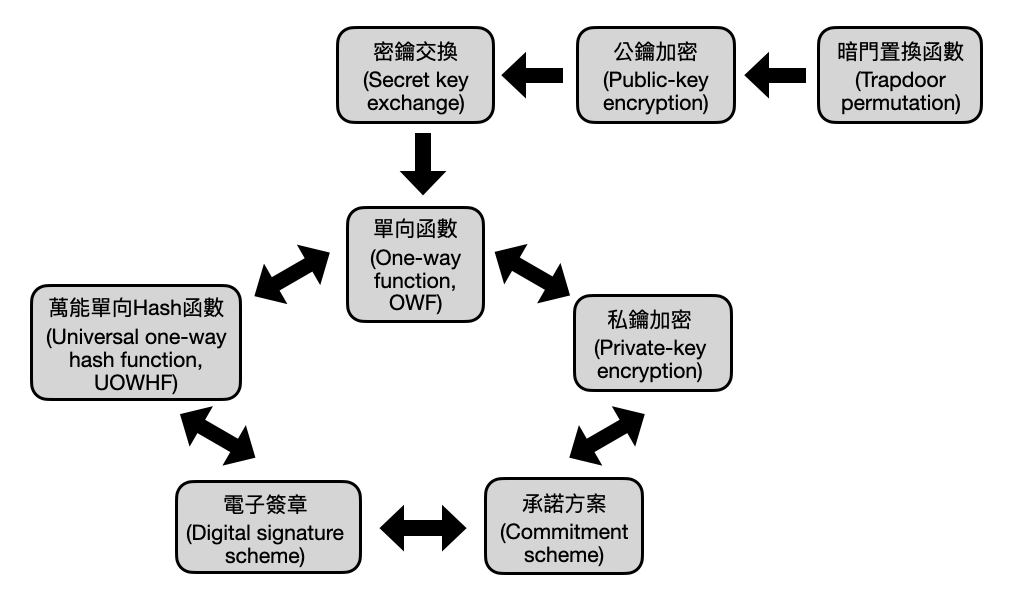
在理論密碼學的世界，學者們更注重密碼設施的安全性。如果說具體的密碼構造是蓋一棟大樓，那麼密碼設施就像是個建築草圖。在構建草圖的階段專家們會更希望能夠快速的檢驗一些新的想法和靈感是不是合乎道理的。因此，假使繼續使用這種貓捉老鼠的方式來檢視密碼設施的安全性，將會非常曠日費時。於是，理論密碼學家受到計算複雜度理論的影響，使用之前介紹的歸約方法，將不同密碼設施的安全性串接成一個大網路。如此一來，只要確保歸約網路中最底層的密碼基礎設施是安全的，那這些透過歸約方法建構在其之上的密碼設施也將會是安全的！

在理論密碼學中，學者們研究不同密碼學設施之間的關係。在圖中如果從A有個箭頭往B，就代表可以利用密碼設施A來構建密碼設施B。如果是雙箭頭，就代表可以互相建構。很可惜的是，在這些常見的密碼設施中，沒有一個是可以在不需要任何假設的情況下就成立。因此，密碼學家總是需要先假設某些密碼設施存在，例如單向函數(one-way function)，然後再透過歸約方法來構建其他的設施。

密碼學與計算複雜度理論，由歸約方法拉出千絲萬縷的和弦，依傍著磅礴的密碼學應用，共譜出動人的二重奏。

機器學習與人工智慧

人類許多的發明和學問時常來自對自身以及大自然的觀察，當我們成功把“計算”這個概念形式化，並在理論與實務上開花結果後，下一個很相關的目標就是：學習。

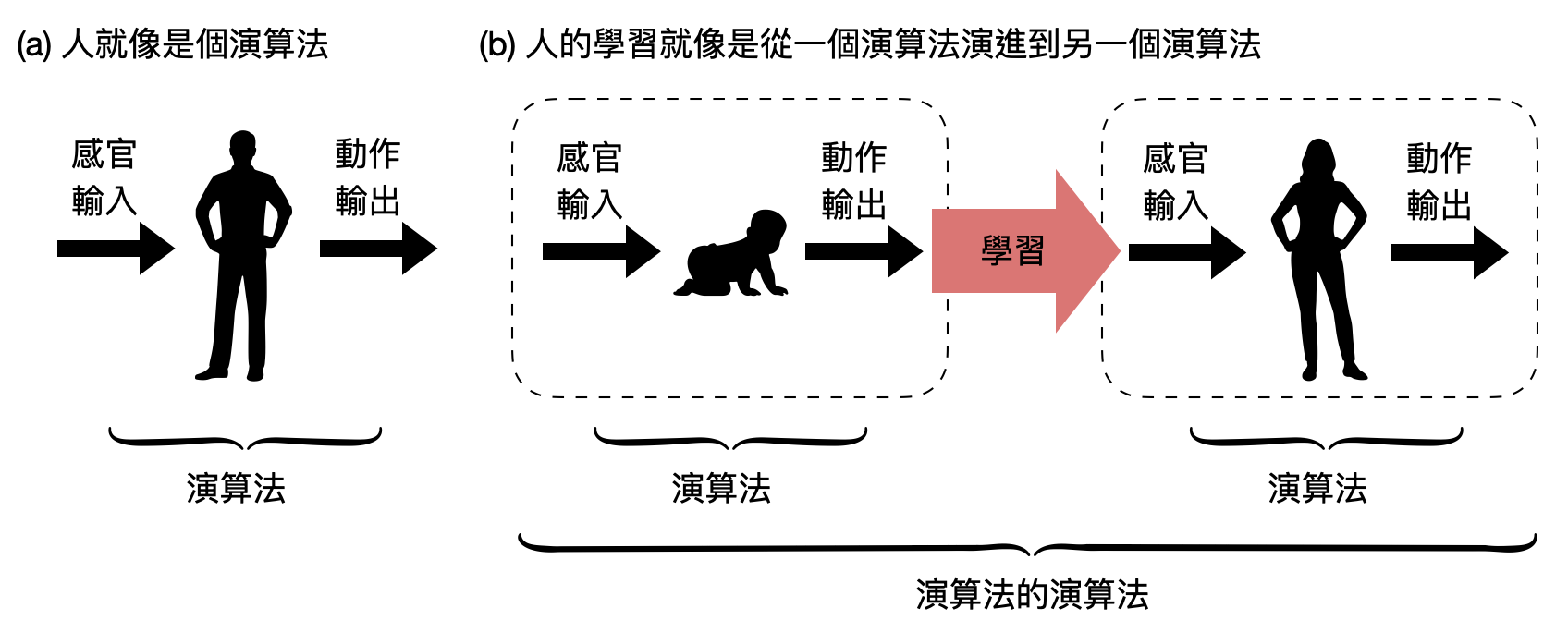
什麼是學習呢？如果把一個人在某個時刻的整體，抽象成將感官輸入對應到動作輸出的一個演算法。那麼學習將會對應到這個演算法的改變。換句話說，學習某種程度是個“演算法的演算法”(或是“計算的計算”)！

(a)一個人根據感官輸入做出動作反應，就像是個演算法一樣。(b)人的成長和學習，會改變所使用的演算法。於是，學習就好像是個演算法的演算法。

該如何將這個抽象的想法形式化呢？我們可以讓機器也會學習嗎！？學習的目標是什麼？是要將目前的計算過程轉換到什麼樣子的計算過程？又或是，學習並沒有那麼明確的目標！？

學習的數學定義

由於學習和計算有著糾纏不清的關係，電腦科學家當仁不讓地在上個世紀末就著手嘗試將“學習”這個概念形式化，試著重現我們在研究“計算”時得到的成功。以下讓我們看看三個常見的數學理論架構：約略近似學習、經驗風險最小化、以及強化式學習。

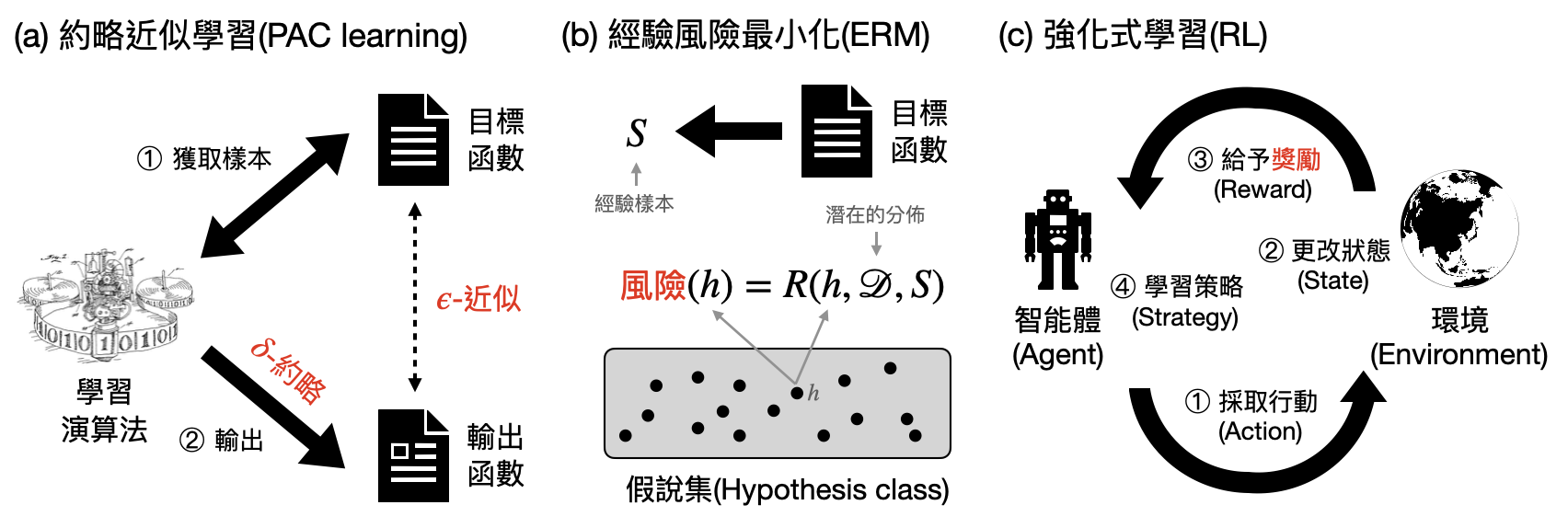
約略近似學習(PAC learning, Probably Approximately Correct learning)源於計算學習理論(computational learning theory)，其核心著重學習時所需要花費的計算資源(參考下圖(a))。就像我們在準備考試時，只有有限的時間可以刷題準備，該如何讓自己有很高的機率考出高分呢？

經驗風險最小化(ERM, Empirical Risk Minimization) 可以說是統計學習理論(statistical learning theory)的基礎公設，其關注的重點是需要蒐集多少資料(data)/樣本(sample)才能達到好的學習效果(參考下圖(b))。假設你第一次考試考砸了需要重考一年，於是有非常多的時間可以好好地吸收所有考古題地精華，該使用什麼樣的答題技巧才能夠在下一次的戰場上脫穎而出呢？

強化式學習(RL, Reinforcement learning) 考慮的是智能體(agent)能夠和環境(environment)互動的設定。環境根據智能體的行動而給予的獎勵，智能體則根據獎勵調整其狀態甚至是策略，目標在未來能夠獲得更多的獎勵(參考下圖(c))。當你加入了一個從未玩過的桌遊，在不知道規則的情況下，該如何透過幾輪遊戲的勝負邊玩邊學，逐漸提高獲勝率？

(a)在約略近似學習的架構中，我們假想有個目標要學到的函數，並且擁有一些樣本及目標函數在這些樣本上的取值。最後的目標是在有限的計算資源下輸出一個函數使得有很高的機會此輸出函數與目標函數非常相似。(b)在統計學習理論中，我們假想有個目標要學到的函數、一個函數的假說集(hypothesis)、以及一個關於樣本(也就是函數輸入)的潛在分佈。最後的目標是找到一個函數能夠在這個樣本潛在分佈下，與目標函數越接近越好，接近的程度則會被一個風險函數給刻畫。而經驗風險最小化是一個準則，會選擇假說集中具有最低經驗風險假說函數。(c)強化式學習透過給予獎勵，以及最大化期望的獎勵數量，來讓智能體學習應對環境狀態的策略。

機器學習模型與學習演算法

有了數學架構之後，就可以開始思考該如何教導機器學習了！電腦科學中逐漸茁壯一個子領域：「機器學習(machine learning)」，就是在專門研究怎麼讓機器也可以和人一樣學習。

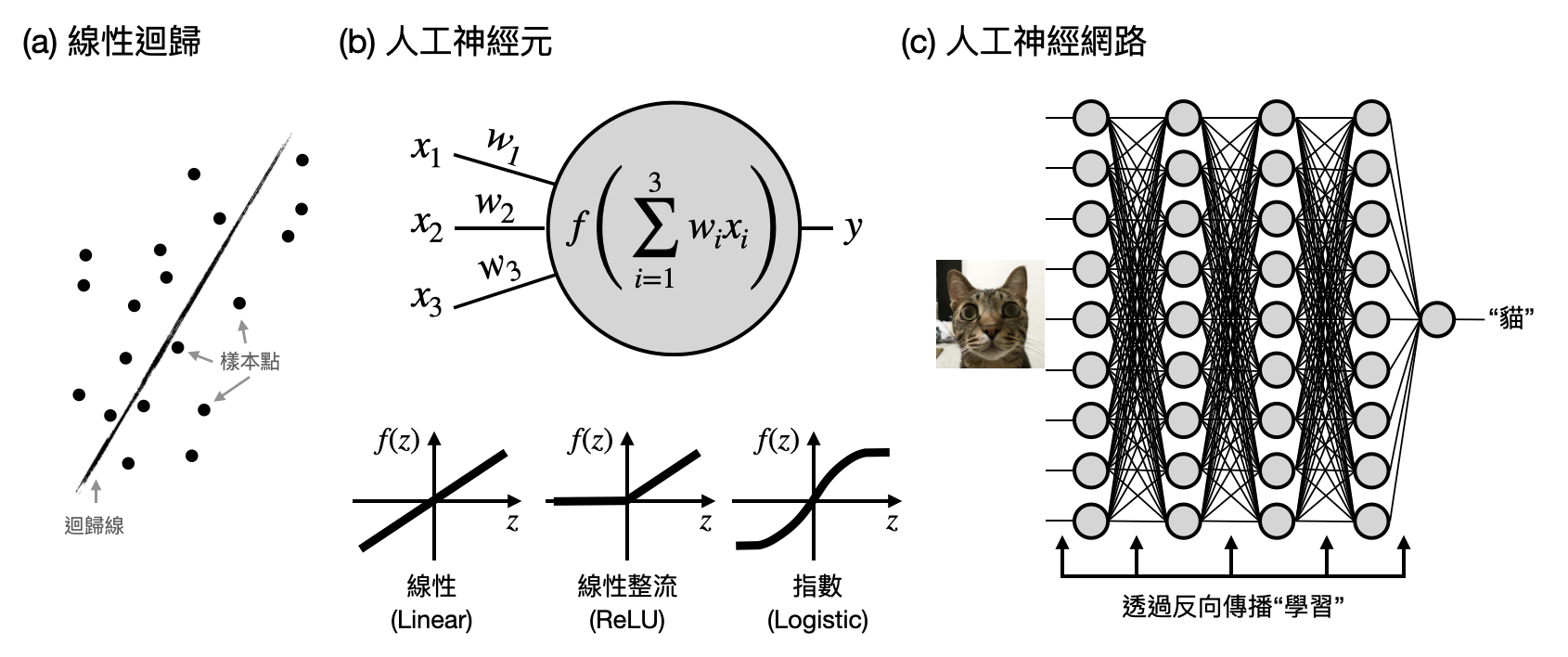
由於學習最終的“輸出”是一個計算過程，所以在機器學習中的研究通常會包含兩大元素：(i)機器學習模型以及(ii)學習演算法。前者提供了輸出的數學形式，後者則是描繪了學習的過程。下圖將提供兩個常見的例子：線性迴歸(linear regression)與人工神經網路(ANNs, Artificial Neural Networks)，讓讀者感受一下。

(a)線性迴歸的目標是從資料的樣本點中，找出一條線可以刻畫這些點的整體趨勢。(b)一顆人工神經元會將輸入值依照不同的比重做線性加總，並餵入一個啟動函數(activation function)作為其輸出。常見的啟動函數有線性、線性整流(ReLU)、及Logistic。其中後兩者因為具有非線性，所以能夠帶來更豐富的表現能力。(c)人工神經網路，或稱類神經網路，就是將許多類神經元連接起來，因而形成了一個函數。例如圖中的類神經網路可以將一張輸入的圖轉化為其物種作為輸出。透過使用大量的訓練資料，學習演算法會根據類神經網路的正確與否來改動連接線的權重(weight)，進而達到學習的效果。

圖靈測試與人工智慧

一旦學習之後，就擁有智慧了嗎？在回答這個問題之前，也許我們先該問問自己什麼是智慧？會打掃家裡是智慧嗎？通過考試是智慧嗎？還是悟出人生的真理才是智慧？

Turing早在機器學習、人工智慧、神經網路等名詞出現之前，就已經在思索類似的問題了。如同他發明圖靈機的先知灼見，Turing在他1950的論文『Computing Machinery and Intelligence』中，提出了“模仿遊戲(imitation game)”的概念，嘗試提出一個標準來判定機器是否有智慧。雖然後世漸漸改用「圖靈測試(Turing test)」來稱呼這個概念以紀念Turing的貢獻，模仿遊戲一詞更是在2014年被使用成為一部關於Turing的電影的片名。

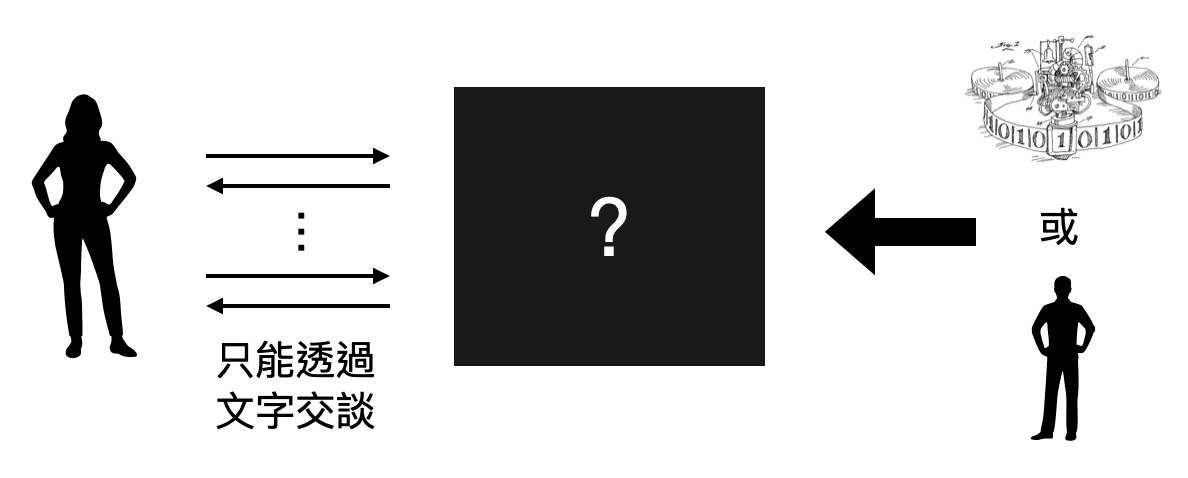
想像有一個審問官(interrogator)只能透過文字和某個不知名的物體交談，他能辨別對方是一個真的人還是一台機器嗎？Turing認為，一旦審問官無法辨別機器與人，那麼機器就已經具有了一定程度的智慧。後來有許多學者提出不同版本的圖靈測試。

在這個聊天機器人一天比一天厲害的年代，你是否曾經懷疑過和你聊天的朋友到底是真人還是機器人！？Turing在七十多年前就想像出這樣的場景，並且提議用此作為判定機器是否有智慧的標準。如果人工智慧能在智力測驗和圖靈測驗上贏過大多數的人類，你會怎麼看？

大模型中湧現的智慧？

數大就是美，難道數大也是有智慧？近年來隨著電腦科技以及資料蒐集數量的大幅提升，電腦科學家們發現只要把神經網路弄大弄深，其表現能力就可以跟著提升，而且看似沒有明顯的天花板！到底如此“湧現”的智慧是怎麼做到的？我們對大模型中湧現的智慧了解有多深？在下圖中讓最近火紅的ChatGPT來解釋一下吧！

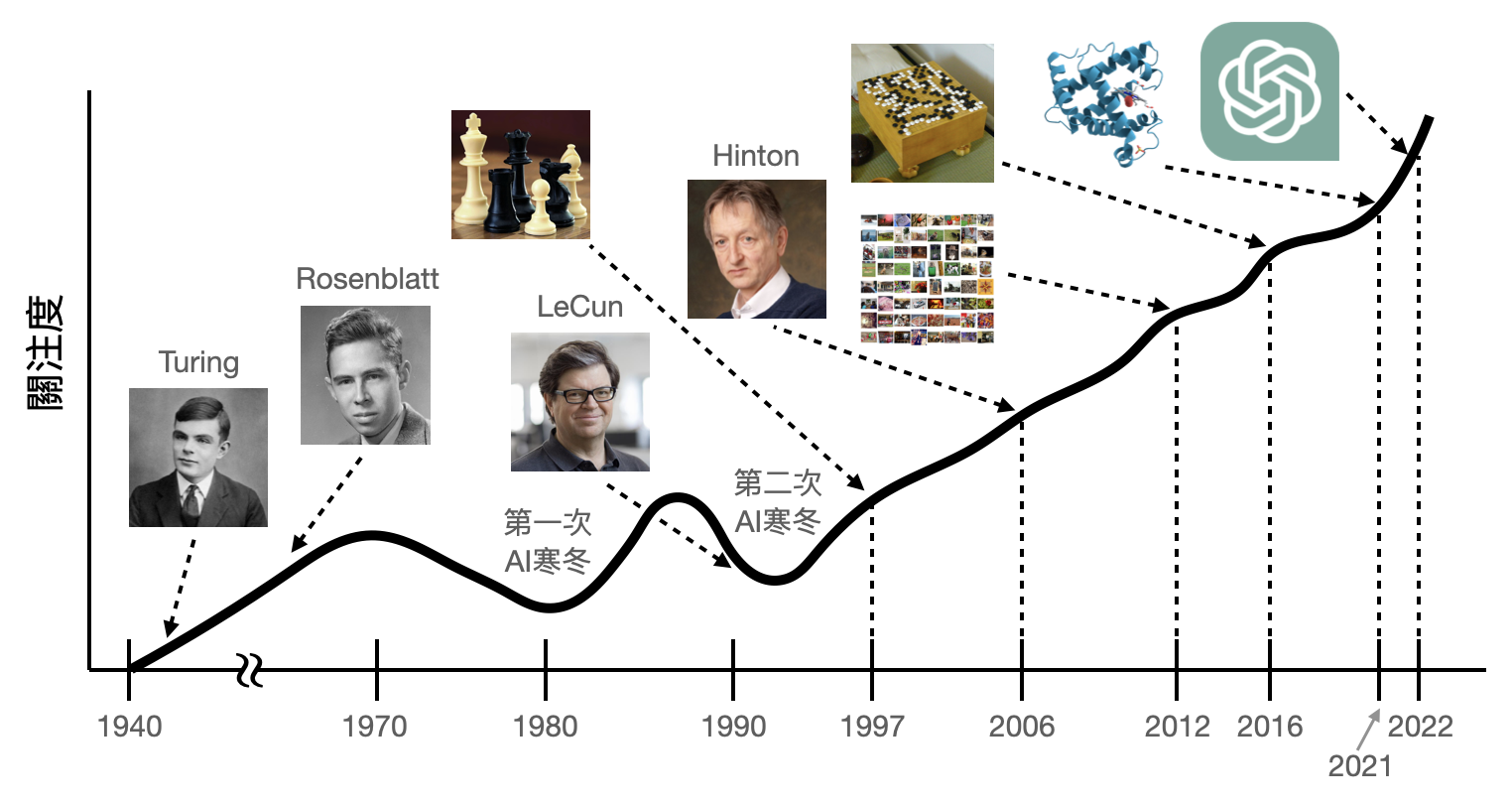
人工智慧帶給我們的下一個驚奇會是什麼？在大模型湧現的能力之外，是否還有其他潛力等著我們發覺？最後讓我們退一步，在下圖中回頭重新咀嚼人工智慧在過去70年間的奇幻之旅。

自Turing在1950年提出了圖靈測試後，越來越多先驅投入人工智慧早期的探索，其中以Frank Rosenblatt在1958年建造出的感知器(perceptron)最為出名。然而，在1970到1980年這段時間，由於電腦硬體尚未成熟，許多理論還沒辦法實現，因此人工智慧的研究進入了第一次寒冬。後來隨著計算能力的提升，人工智慧與機器學習再次浮上檯面。然而，由於演算法和資料的缺乏，在80年代末期90年代初期間人工智慧的研究進入了第二次寒冬。不過Yann LeCun頂著嚴寒，仍然持續開發如卷基式神經網路(CNNs, Convolutional Neural Networks)等在未來重要的人工神經網路模型。在1997年，IBM的深藍(Deep Blue)擊敗了當時的西洋棋世界冠軍Garry Kasparov。在2006年，Geoffrey Hinton提出了深度神經網路(DNNs, Deep Neural Networks)的概念並著手實現。在2012年，Alex Krizhevsky、Ilya Sutskever、與Hinton實作的AlexNet(用到了CNNs和DNNs的概念)，在ImageNet圖像辨識大賽獲得空前的勝利，震撼全世界。隨後，DeepMind的AlphaGo在2016年擊敗頂尖圍棋好手李世石，DeepMind在2021年的AlphaFold在蛋白質結構問題上取得重大突破。在2022年末，OpenAI公布的ChatGPT讓全世界的用戶驚豔於其湧現的強大語言能力。在下一個五年十年，AI會帶來什麼呢？

總結

在本章中，我們看到了理論電腦科學的一個核心技術：歸約方法。透過計算問題、甚至不同計算模型之間的轉換，我們可以將大量看似繁雜不同的事物，歸約到少量的關鍵點上。Cook-Levin定理打開了NP完備理論的大門，再由Karp承接並大規模地展示了NP完備問題的普及性，接著歸約方法被廣泛用在理論電腦科學的各個子領域、遍地開花，最後驀然回首大家又發現不同子領域之間有著極度緊密的連結。

然而，當歸約方法將計算世界牽成了一個大網絡之後，在網絡最中心處的核心計算問題仍是遲早要正面面對的。筆者認為理論電腦科學目前正進入了“巴洛克時期”，各式各樣壯碩華麗的數學構造在令人敬佩之際，是不是也讓人眼花撩亂、迷失了方向？

至於人工智慧這一端，從當年理論學家熬過漫長的寒冬，提出前瞻性的模型與學習演算法，終於在近年來隨著硬體與資料量的爆炸性成長，跟著湧現令人瞠目的表現。如今實務反過來超車理論，在如此令人興奮的時代，計算與學習理論的下一步要往哪裡走？

延伸閱讀

教科書與其他教材：

內文提及的論文：

科普書籍：