Chapter 4
A Bottom-Up Determinism - Classical Mechanics
Nature is pleased with simplicity. And nature is no dummy.
Isaac Newton
物理是門研究自然世界的學科,關注物體的組成、運動、時間和空間等等。如果真要用一句話來總結,我會說物理的核心思想是在找尋和理解事物的“本質”。而什麼是“本質”呢?可能每個人心中想的或多或少都不太一樣,而身為最古老的科學領域,物理學用幾百年的時間建立了一些物理學家們公認的價值系統,這些系統又以數學模型的方式被呈現。然而和數學不一樣的是,物理根本的目標還是在於建立對世界的理解,衍生出來的數學再怎麼漂亮華麗,終究還是得回歸現實。
在近代科學發展中,尤其是電腦的計算能力在21世紀崛起後,許多物理學家漸漸開始跨界到其他的科學領域。對非物理專業訓練出生的人來說,物理學家思考和呈現研究結果的方式可能會看似“沒什麼用”或是“不知道該如何解讀”。同樣的,當提及計算和物理糾纏的關係時,如果不先試著建立一些物理學的審美觀,就很容易落得霧裡看花。
物理作為理解世界的模型
在之前的章節中,我們提到了數學是個嚴謹的形式語言,可以幫助人們抽象地分析和思考各種事物。於是很自然的,物理學中許多理論都是建構在數學語言之上。透過從物理世界獲得的啟發,甚至還能夠讓人發明/發現新的數學系統。然而和數學不一樣的是,物理根本的目標還是在於建立對世界的理解,衍生出來的數學再怎麼漂亮華麗,終究還是得回歸現實。那物理學到底是用什麼方式來理解世界呢?所謂“物理模型”又到底是什麼意思?這些理解和模型跟計算又有什麼樣的關係?讓我們跟隨歷史發展的脈絡,一步一步走進物理的世界。
牛頓與他的前輩
在中學的時候,很多讀者可能都學過牛頓三大定律,說不定有些人可能還深受其計算所擾吧!然而,不知道你的高中老師有沒有講過到底為何牛頓定律如此重要?為什麼到大學之後牛頓力學卻逐漸從檯面上消失了?
在認識牛頓力學的重要性以及它和“計算”的關聯時,我們需要先來瞥一瞥相關的歷史發展。
在古希臘時其實就已經有許多先驅在研究和思考物理世界的運作機制,例如著名的大思想家亞利斯多德(Aristotle, 384BC-322BC)。細節這邊就先不論,單從結果來說,這些世紀前對物體運動的理解大多還停留在臆測階段,而且跟近代科學最本質的差別就是他們尚未建立一套系統,可以清晰地了解系統內發生的狀況,並從中對現實世界做推論。
一直到中世紀的哥白尼(Copernicus, 1473-1543)和伽利略(Galileo, 1564-1642),人們才開始對某些特定的課題(例如天體運行、自由落體等等)有了一些初等的理解。和之前完全不同的是,哥白尼和伽利略都能夠提供一種“機械性的理解”,只要照著一些數學規則做運算,就可以很精準地預測物體的運動軌跡。
牛頓(Newton, 1642-1727)曾說過:「如果我能夠看得很遠,是因為站在了巨人們的肩膀上」。如今,牛頓自己也成為了現代物理巨人中的巨人。而他在物理學中最重要的貢獻之一,就是牛頓定律。
為什麼牛頓定律很重要呢?他和之前哥白尼及伽利略的理論相比有什麼見長之處?我個人認為牛頓定律有兩個在思想層面重要的意義:
嘗試對力學有個統一的理解: 牛頓定律嘗試去解釋的是“任何”物理系統的運作,當然在應用時會需要做許多理想化的假設,但不像哥白尼和伽利略專注在研究天文領域或是某些特定現象,牛頓提出的架構沒有針對過於特定的系統,可以套用在非常廣泛的應用場景上。換句話說,牛頓定律本身可以被解讀為一個假設,認為“所有”物體的運作可以被簡單幾個規則解釋,不需要每次遇到一個新的問題就重新設計模型。(看過之前數學部分章節的讀者,有沒有覺得這和圖靈機的願景似曾相似?)
公設化的理論系統: 如前所述,牛頓提供的大統一理解奠基在幾條簡單的“公設”,一旦遇到不同的現象時,再把這些規則套用上去做計算。如此從“第一原理(first principle)”的方法論出發,可以把現實世界和抽象世界乾淨地劃分開來。也就是說,一旦假設並且相信這些基本公設正確地描述了物理世界,人們便可以直接在理想的數學模型中做各種運算和預測,最後再回來和現實情況作比較。
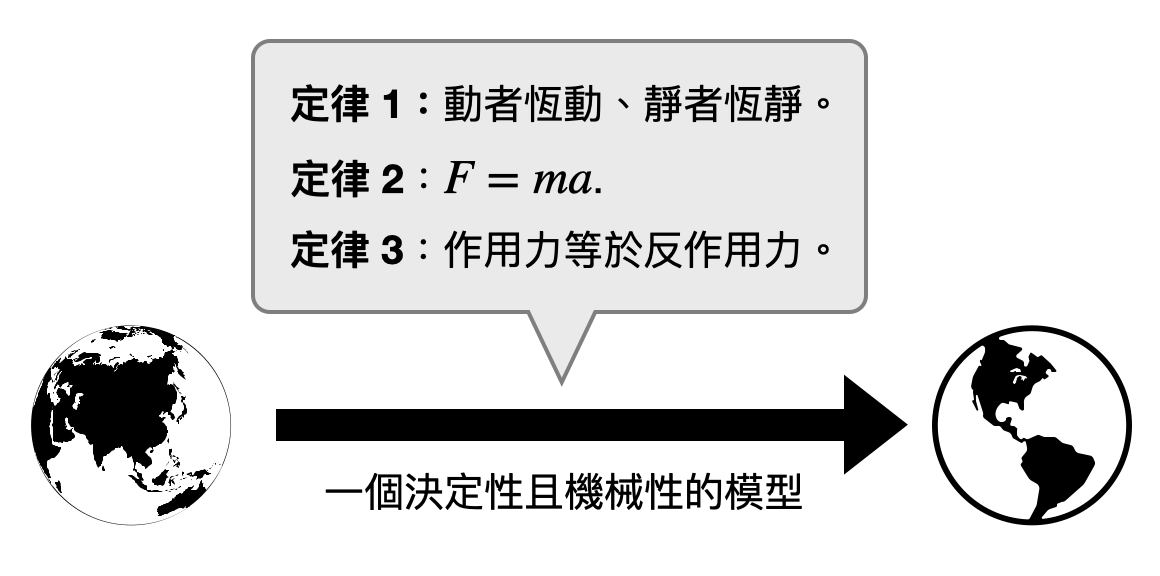
牛頓定律在日常生活中甚至是工程領域中,都能提供非常精準的描述和預測。更進一步,牛頓做的貢獻在本質上提供了一個“計算模型”來理解物理世界。一旦給定了一個系統的初始狀態,透過不斷套入三大定律(或是一些額外的定律像是萬有引力定律),並解開所有相關的方程式,我們就可以預測這個系統中所有物體的運動軌跡。而這正是中學物理考試中不斷出現的計算題!
這樣看起來哥白尼、伽利略、牛頓等人已經成功地把對物理世界運行的理解,轉換到相對應的計算模型。只要透過一系列機械性的操作,帶入公式和化簡,就能夠完整描述一個系統。如此的“理性之夢”或是說“機械之夢”是故事的結局嗎?從現在往回看,很顯然這只是一切的開端而已!
物理模型與計算:以力學為例
什麼叫做「一個力學理論」呢?在研究一個物理系統時,裡頭會有我們感興趣的物體,這些物體會隨著時間演化改變狀態,同時我們又擁有一些觀測方式可以獲得關於物體狀態的一些資訊。於是,一個力學理論需要替這些元素建立相對應的數學模型/描述:(i)系統狀態的數學模型、(ii)系統演變的數學規則和(iii)觀測的數學模型。
例如在牛頓力學中,一個物體被抽象成一個「點」,可以在三維的歐式空間中移動。接著,給定系統的初始狀態,牛頓定律告訴了我們系統中的物體回如何改變位置、速度等等的狀態。最後,我們可以對各種系統的狀態(例如位置、速度等等)有精確的測量。
也就是說,一個力學理論(或是更廣義的來講一個物理理論)提供了一個描述世界的數學模型,以及其中狀態改變的規則。一旦給定了初始狀態,我們就可以直接照著這些規則來計算系統的演化過程。如此一來,一個力學理論是不是很像一個演算法呢!?
不過和演算法很不同的地方在於,力學理論中的演化規則是在設計完理論架構的當下就被決固定了,如果你拒絕牛頓三大定律然後自創一些新的規則,那麼接下來你建構出的物理理論就不再屬於牛頓力學。而如果又有人拒絕你的物理理論並另創門派,那將又會是另一個新世界。於是,對於物理學家來說,創立新的力學/物理理論固然重要,相同重要的是去仔細研究一些常見的系統狀態設定,並了解它們在一個力學系統中詳細的演化過程是怎麼一回事,有沒有符合實際情況?有沒有出現一些新奇的物理現象?
力學理論和計算之間有什麼異同之處呢?再更深入探討這個問題之前,先讓我們學習四個物理理論(古典力學、統計力學、量子力學、重力理論)的基本概念,希望藉此可以讓讀者建立一些心理圖像,替之後的討論打下一些共同基石。在這四個物理理論中,古典力學和統計力學相對比較基礎,但是其中的世界觀對於物理和計算之間的連結非常關鍵。至於量子力學和重力理論,則是對近年來理論計算機的發展注入了不少啟發。
由於本書並不是物理教科書,所以勢必會省略許多細節,甚至在某些部分可能會有些不精確之處,歡迎來信給予任何指正和建議!
古典力學
古典力學(或稱經典力學, classical mechanics)泛指處理一般日常尺度(相較於量子理論處理極度微觀的世界,和重力理論處理極度宏觀的世界)的力學理論。以下,讓我們從牛頓力學開始,試著以和演算法做比較的角度來重新認識物理理論。
牛頓力學
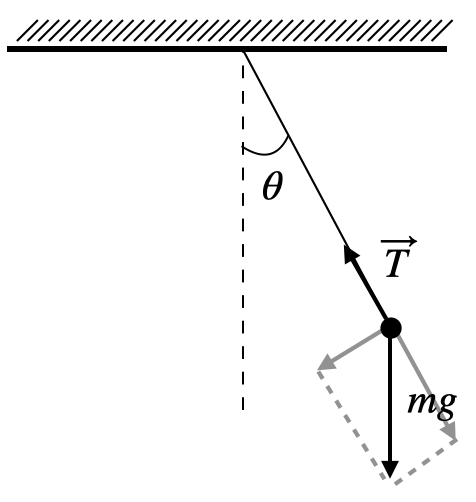
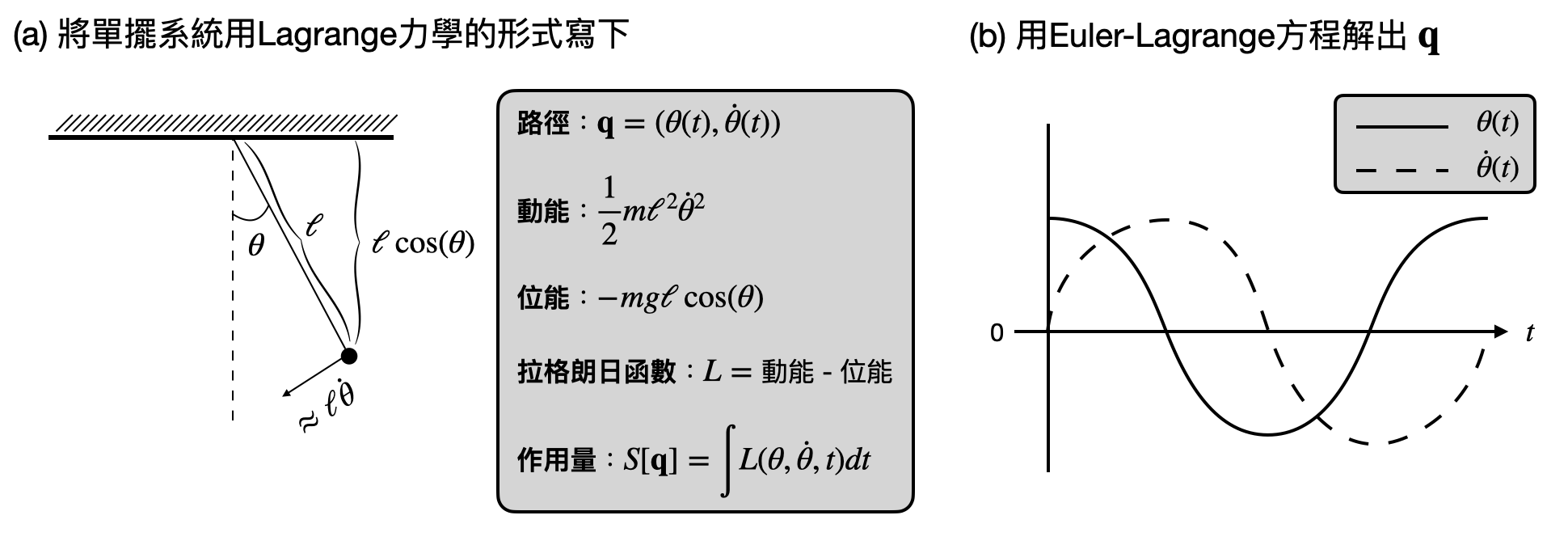
在這邊讓我們將牛頓以及其之前(例如伽利略)的力學發展通稱為牛頓力學,在一個我們感興趣的系統中,物體會被數學描述成(三維)歐式空間中的一個點。而系統的演化過程則會被牛頓定律以及重力理論等等描述。以常見的單擺為例,我們知道物體受到了重力以及繩子的拉力,由於物體只會沿著切線方向移動(要不然繩子會產生形變),所以我們可以根據物體目前所在位置的角度,計算出重力與繩子拉力之間的關係,進而推導出切線方向的外力為何。接著,一旦知道外力的大小和方向,根據牛頓第二定律就可以算出物體的加速度為何。最後,帶入物體的初始狀態,我們就可以計算出在任何一個時間點物體的位置、速度和加速度。
如果上一段的討論讓你暈頭了,不用太擔心,這邊主要的目的只是讓讀者感受一下使用牛頓力學的過程。現在讓我們往後退一步,想想看牛頓力學到底給了我們什麼。
我們可以發現到,牛頓力學提供了一個“動態”的計算過程來認識一個系統的演化。也就是說,給定一個當下狀態,我們可以透過規則計算出下個瞬間系統會演化到什麼狀態。是不是跟圖靈機非常相似呢!?如此動態的描述,透過將時間切成許多小區間,我們就可以透過模擬一個系統從每個小時間區間的起點會走到哪個終點,進而獲得系統完整的演化過程。為了得到系統演化的公式解,牛頓甚至發明了微積分來處理將時間切成無限小區間之後的計算。
然而,當系統中物體的個數變多時,在牛頓力學的框架下計算系統變化將會變得非常複雜。這也是為什麼到了大學後,物理系學生立刻需要學一套新的力學理論:「拉格朗日力學(Lagrangian mechanics)」。
拉格朗日力學
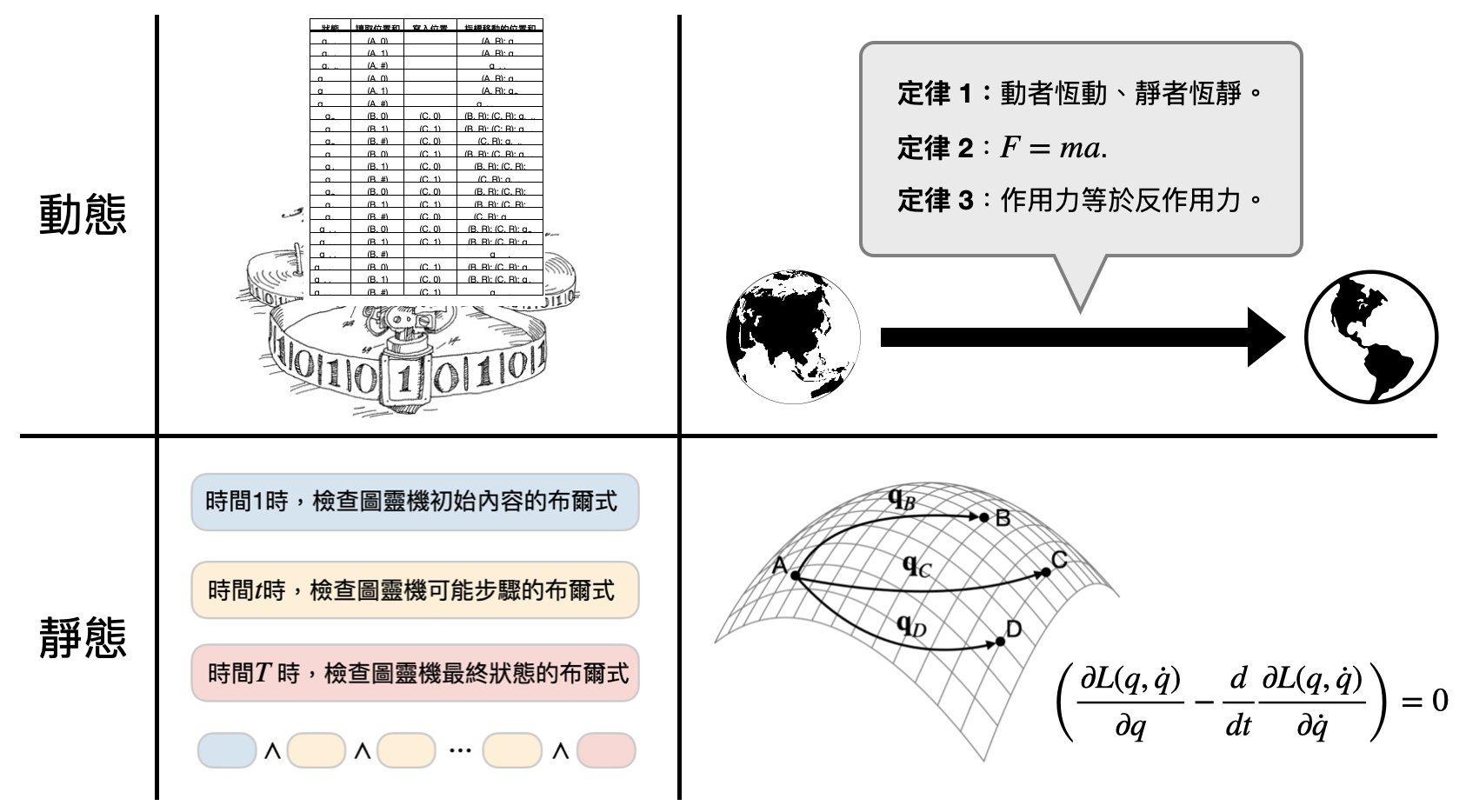
相對於“動態”的牛頓力學,拉格朗日力學可以說是個“靜態”的力學理論。在好好解釋“靜態”指的是什麼意思之前,讓我們廢話不多說直接看看拉格朗日力學的世界觀是什麼吧!
之前我們提到一旦系統中有很多的物體後,牛頓力學的計算將會變得過於複雜。主要的原因在於牛頓把不同的物體當作獨立的角色,因此必須很詳細的紀錄物體之間互動造成的影響。而在拉格朗日力學的數學模型中,我們將不再把系統中的物體分開討論,而是將它們共同的位置、速度等等放在一起討論,把整個系統的狀態當作一個高維度空間的一個點!
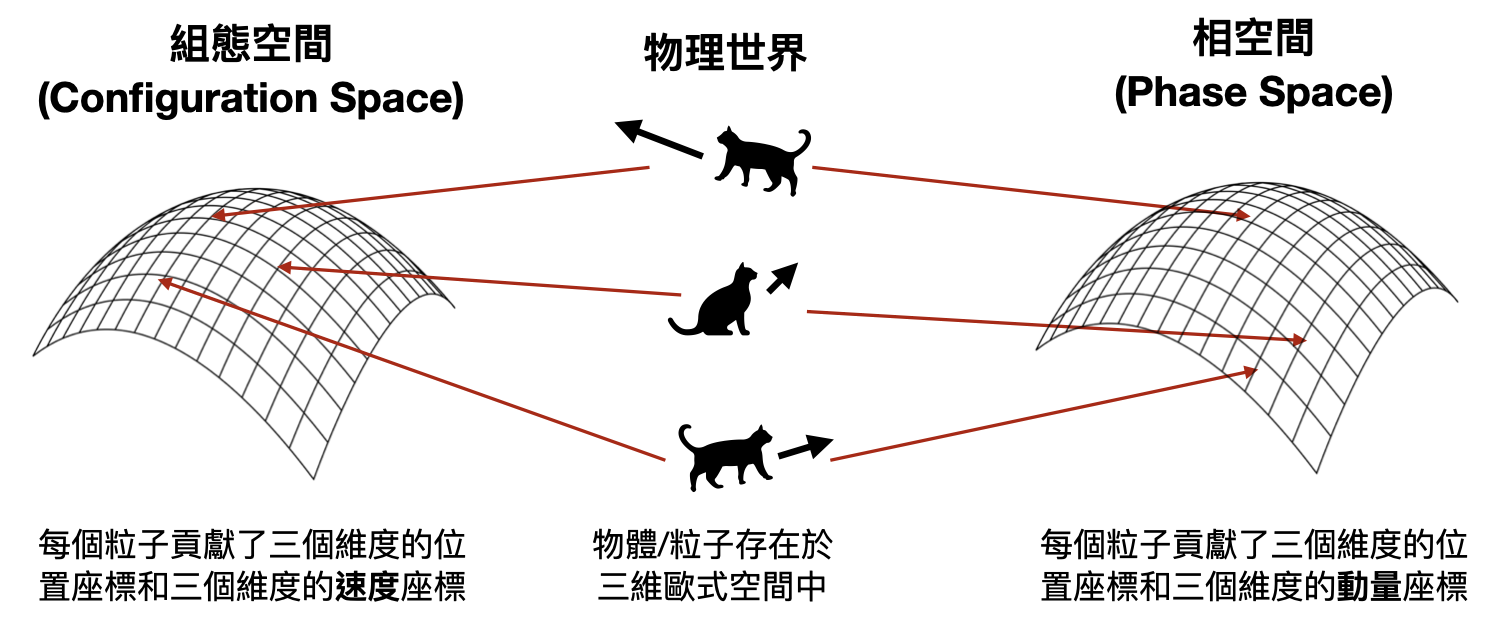
具體來說,考慮有$N$個物體的系統,假設每個物體被六個變數刻畫著:三維空間的位置坐標以及三維空間中的速度向量(位置和速度在古典力學中被假設維互相“獨立”的變數,就像在牛頓第一定律中一樣)。於是整個系統的在某個時間點的狀態,可以對應到某個$6N$維空間的一個點。於是,系統狀態的演化就被這個$6N$維空間中的點的變化所描述。這個$6N$維空間又被稱為「組態空間(configuration space)」。
那麼這個$6N$維空間中的點是如何演化的呢?注意到,雖然在物理世界中同時有許多粒子在變化,然而在組態空間中,對應到的只是一條路徑而已。當牛頓力學著重在描述系統中下一個狀態為何的時候,拉格朗日力學則告訴我們應該直接關注系統在一段時間內的演化路徑!
更令人讚嘆的是,在拉格朗日力學中,竟然只要一個函數就可以完整的刻畫系統的演化了!而這個函數又被稱為「拉格朗日函數(Lagrangian)」。
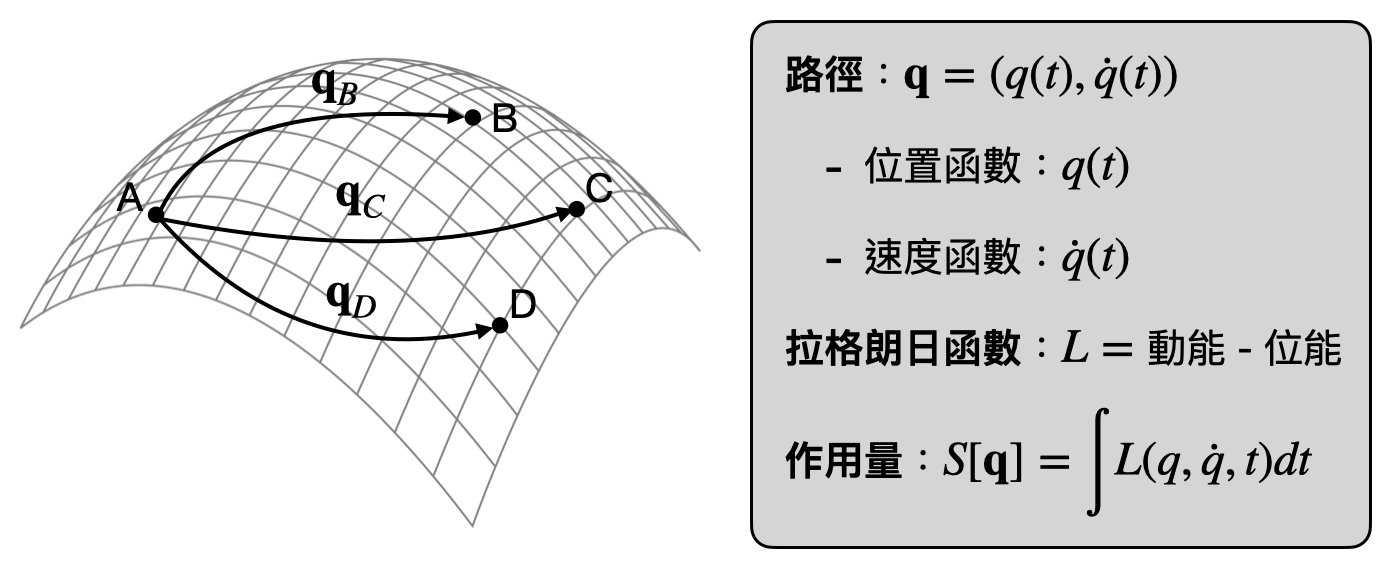
拉格朗日函數將每個組態空間中的點都對應到一個數值。具體來說,一個狀態的拉格朗日函數值,是被定義為系統中的動能減去位能。對於組態空間中的一條路徑來說,我們可以根據拉格朗日函數計算出這個路徑所需個作用量(action)。也就是說,如果系統照著這個路徑演化的話,會需要消耗(獲得到)多少的能量(如上圖)。
拉格朗日力學:理解一個系統的動力學可以透過拉格朗日函數來研究演化路徑的作用量。
最後,拉格朗日力學的核心定律就是,系統會選擇使用最小作用量的路徑!這又被稱為「最小作用量原理(principle of least action)」或漢米爾頓原理(Hamilton’s principle)。
最小作用量原理(Principle of least action):系統的演化會根據作用量最小的路徑。
於是,在拉格朗日力學的體系中,計算系統的演化過程變成只需要(1)設定好初始狀態(每個粒子的位置和速度),(2)寫下拉格朗日量,(3)寫出路徑的作用量,(4)計算出作用量最小的路徑。當在牛頓力學中我們需要動態地刻畫每個物體的演化,在拉格朗日力學中,我們只需要靜態地算出最小作用量的路徑就好了。
拉格朗日力學的世界觀:(1)設定好初始狀態,(2)寫下拉格朗日量,(3)寫出路徑的作用量,(4)計算出作用量最小的路徑。
該如何算出最小作用量的路徑呢?在物理中常見的做法是,算出一條“穩定的路徑”。
變分分析與Euler–Lagrange方程式
當給定了一個系統的拉格朗日量之後,該如何計算出系統演化的路徑(也就是作用量最小的路徑)呢?不像電腦科學家總是想要找到一個能夠處理所有可能情況的方法,對物理學家來說,他們著重在所謂“符合物理的情況”,這些情況通常相對容易處理,並且可以透過一些也許不是在數學上完全嚴謹的方式,得到在物理上正確的理解。
其中一個最常見的分析方式,就是「變分分析(variational analysis)」,讓我們來看看它可以如何幫助我們計算古典力學中的演化路徑。
在拉格朗日力學的架構中,系統的作用量$S$是定義在每一條可能的演化路徑上。於是,我們也可以把作用量看作是一個將路徑對應到一個數值的函數。由於路徑本身也是一個函數(將時間對鏡到一個空間中的位置/狀態),所以作用量$S$這種類型的函數在數學上又會被稱作為一個「泛函(functional)」。因此,找出系統的演化路徑,將會等價於找出一個泛函的最小值。
變分分析的核心概念,是考慮一條“任意”路徑$q$,考慮其“任意”微小變化(也因此得名“變分”)$\delta q$的作用量$S[q+\delta q]$。如果$q$是條作用量最小的路徑,那麼我們應該會得到$S[q+\delta q]\geq S[q]$。注意到,這邊我們考慮了所有可能的微小變化$\delta q$,參考下圖(a)的幾何圖像。
所以現在我們的目標變成是要找到一條路徑$q$,使得對於所有的微小變化$\delta q$,都有$S[q+\delta q]\geq S[q]$。這樣看起來怎麼好像讓問題變得困難了?此時數學分析的神妙之處就大展身手了!以下的「Euler–Lagrange方程式(Euler–Lagrange equation)」是個確保$S[q+\delta q]-S[q]=0$的“充分條件”(本小節末附有詳細說明)!
Euler–Lagrange方程式(Euler–Lagrange equation):$\left(\frac{\partial L(q,\dot{q})}{\partial q}-\frac{d}{dt}\frac{\partial L(q,\dot{q})}{\partial \dot{q}}\right)=0$。
總結來說,古典力學的新世界觀告訴我們不必再像牛頓一樣忙碌地追蹤著系統中物體時時刻刻的變化,只要寫下拉格朗日函數,接下來只要面對幾條Euler–Lagrange方程式,解出滿足其條件的路徑$q$就好了。
同時,拉格朗日力學和牛頓力學其實是在數學上“等價”的!也就是說,對於同一個物理系統,同一個初始狀態,牛頓力學和拉格朗日力學會給出一樣的預測。兩者的差異只在它們各自是如何描述和計算系統的演化。
面對同一個世界,如果改變自己的世界觀,從此可能海闊天空。
由於我們只考慮在$q$附近非常微小的路徑變化,所以$S[q+\delta q]-S[q]$可以被以下乾淨的方程式近似的很好!(以下式子是針對一維系統,對於其他更高維度的系統可以針對每個維度各自寫下這個方程式)
\begin{equation*} S[q+\delta q]-S[q] = \int dt \left(\frac{\partial L(q,\dot{q})}{\partial q}-\frac{d}{dt}\frac{\partial L(q,\dot{q})}{\partial \dot{q}}\right) \delta q \, . \end{equation*}
對於微積分不熟悉的讀者不用害怕,讓我們來解讀一下上面這個式子的直覺含義。
首先式子的左邊是路徑$q$在做了$\delta q$變化後,系統作用量的變化,也就是我們希望這個變化量是非負的。再來,式子的右邊則是一個對時間的積分,從路徑起始之際開始計算在每個時間點系統作用量的變化為何。而這個方程式告訴了我們每個瞬間系統在$q$和$q+\delta q$之間作用量的差距是和某個偏微分式子(也就是大括號中的那些東西)相關。在這邊還沒學過微積分的讀者可以先相信我們,這個偏微分式子是非常容易從拉格朗日函數$L$算出來的。
最後重點來了,雖然要算出總共作用量變化$S[q+\delta q]-S[q]$是否非負在最廣義的情況下還是不容易,然而從這些式子和討論中,我們可以看到一旦上面公式右手邊大括號中的數值一直都是0的話,那就可以保證$S[q+\delta q]-S[q]\geq0$了,這個想法被上述的Euler–Lagrange方程式刻畫。於是,只要算出Euler–Lagrange方程式的一個解$q$,就可以確保$S[q+\delta q]-S[q]=0$,因此路徑$q$會是系統的一個穩定狀態。
混沌與Liouville定理
古典力學的世界觀,似乎暗示我們一旦只要知道一個系統(甚至是我們所處的世界)的初始狀態,就可以根據一些基礎的數學公式,推導出系統會如何演化。那為什麼到現在天氣預報還是常常不準?為什麼幾乎不太可能預測地震發生的時間?
在使用複雜的科學哲學論述探討物理理論和現實的差距之前,光是在抽象的數學層次我們就已經可以解釋上述這兩個問題了:那就是混沌現象(chaotic phenomena)。
在日常語境中時常提到的“蝴蝶效應”,說到一隻南半球的蝴蝶拍一拍翅膀,可能會引起北半球的一場颶風。在數學和物理上的混沌現象和此概念有點相似,而且更豐富!
混沌(chaos):就算初始的狀態可以完全決定了未來的狀態,近似的初始狀態將無法近似未來的狀態。
在直覺上,某隻蝴蝶拍翅與否(系統的初始狀態)可能造成完全不同的天氣結果(系統的未來狀態)。或是氣象觀測數據和地質測量結果的些微誤差,將可能導致最終預測與實際情況的巨大差別。如此一來,就算系統完全遵照古典力學的規則在運作,一旦沒辦法無比精準地測量初始狀態,就不可能準確計算和預測出未來的狀態。
在物理上,如何定義混沌(尤其是量子混沌)至今可以說仍尚未完全取得共識(感興趣的讀者可以參考延伸閱讀)。不過在數學上,我們可以從兩個角度來加強對混沌現象的理解。
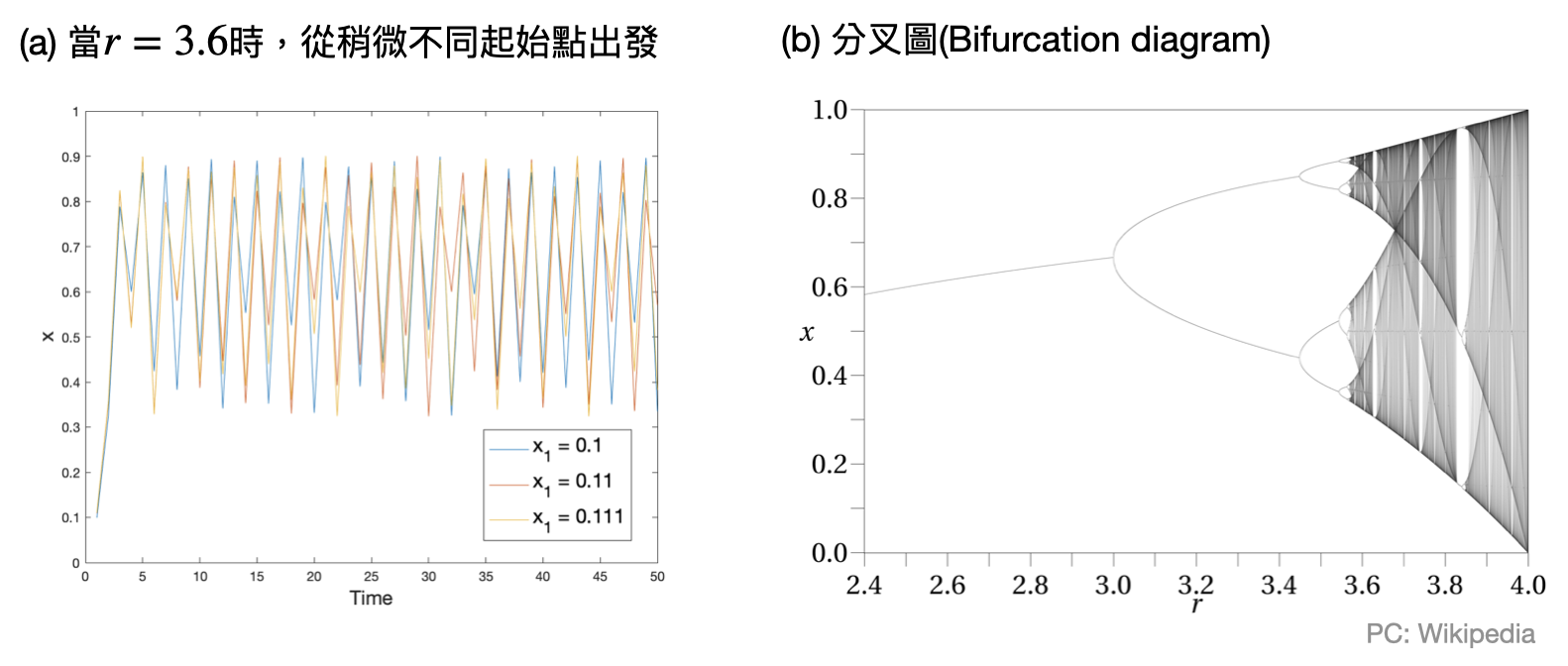
首先,即使是很簡單的一維動力系統(dynamical system),都有可能具有混沌現象。例如,單峰映射(logistic map),其定義如下:從介於0和1之間的起始值$x_0$開始,對於所有的時間$t=1,2,\dots$定義$x_t=rx_{t-1}(1-x_{t-1})$,其中$r$是個在0到4之間可以調整的參數(為了確保$x_t$可以維持在0到1之間)。
直覺上來說,我們可以把$x_t$想成介於0和1之間的數,代表在時間$t$時,系統中人口數相對於最大人口數(例如100億)的比例為何。在單峰映射$x_t=rx_{t-1}(1-x_{t-1})$中,我們可以將公式解讀為下個時間點$t$的人口比例$x_t$會受到兩種因素的影響:(i)$x_{t-1}$對應到人口的繁殖速率和當下人口數成正比,以及(ii)$(1-x_{t-1})$對應到當人口接近最大負荷量時,可能會造成饑荒而使接下來的人口數下降。對於不同的$r$值,單峰映射將會具有很不一樣的性質!例如當$r$介於0和1之間時,不管初始的$x_0$為何,最後當$t$很大的時候,$x_t$都會趨近於0。然而當$r$是3.6時,那麼單峰映射將具有混沌性質,也就是說對於兩個不同但是非常接近的初始值$x_0$,當$t$很大的時候,各自對應的$x_t$將可能會不太一樣。
第二種思考混沌的數學角度則是著重在幾何的觀點。之前我們曾約略提過除了拉格朗日力學之外,古典力學中另外有個漢米爾頓力學的形式,能夠提供一個更清晰的幾何圖像。當拉格朗日力學討論的是組態空間時,漢米爾頓力學考慮的是所謂的相空間(phase space)。簡單來說,兩者的差別在於,組態空間的各個坐標軸對應到了各個粒子的位置維度或速度維度,而相空間的各個坐標軸則是對應到各個粒子的位置維度或“動量(momentum)”維度。由於動量和位置的共軛關係(根據Noether定理,動量是位置平移對稱性相對應的守恆量),相空間將具有所謂的辛幾何(symplectic)結構。這邊我們當然不可能也不打算一一解釋前幾句出現的一堆看起來可怕的數學名詞,不過我們可以用以下這個重要的Liouville定理來讓讀者感受漢米爾頓力學和相空間的美妙,並且順便從幾何的觀點體會(多體系統的)混沌現象。
Liouville定理(Liouville's theorem):在漢米爾頓力學中,系統的演化不會改變相空間中體積的大小。
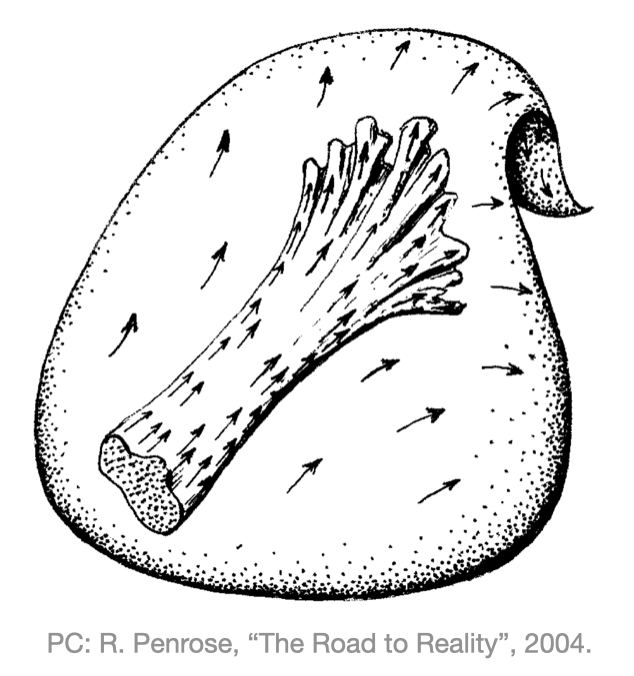
從Liouville定理與相空間的視角,我們便可以將混沌具象化如下:一個系統在演化時,從相空間的一隅,在保持體積的情況下,逐漸擴散至整個相空間。那隻蝴蝶是否知道,它幽雅的舞姿有可能攪和某個風平浪靜的高維空間?
古典力學與計算
恭喜讀到此處的讀者已經完成一趟小小的古典力學之旅,接下來我們將利用這些剛學會的“世界觀”,來看看一些古典物理世界和計算的關係。
在本章剩餘的篇幅中,我們將看到四個不同的小主題:
- 牛頓力學到古典力學(尤其是拉格朗日力學)的進程和Cook-Levin定理的相似之處。
- 多體問體如何挑戰延伸版的Church-Turing論題。
- 混沌和隨機性及偽隨機性的曖昧關係。
- 拉格朗日力學和某個重要演算法的關聯。
重新回顧Cook-Levin定理
還記得第一個NP完備的計算問題是怎麼來的嗎?Cook-Levin定理透過將圖靈機的動態計算過程,轉換成一個靜態的計算問題,檢查是否存在一條合法的計算路徑。如此在動態與靜態計算之間的轉換,是不是和牛頓力學與拉格朗日力學(以及漢米爾頓力學)有著異曲同工之妙呢!?
這樣的關聯,不只是古典力學僅有的,在之後章節將會看到的量子力學中,也會出現如此動態與靜態之間的轉換。有了這個觀察,可以幫助我們在不同的情境之下,根據方便性,選擇合適的視角來檢視人工世界和物理世界的計算。
延伸版Church-Turing論題與多體問體
如果說Church-Turing論題為計算理論打下了根基,那麼延伸版Church-Turing論題(extended Church-Turing thesis)則是在替計算理論的近代發展背書。
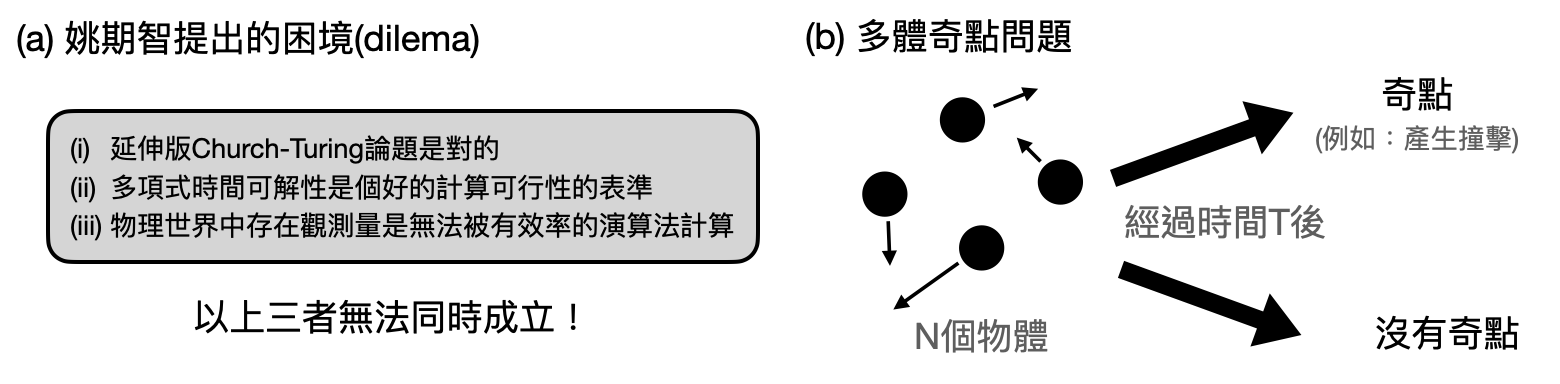
延伸版Church-Turing論題:所有現實世界中可行的計算方法,都可以被一台圖靈機在多項式時間以內的超支中模擬。
換句話說,延伸版Church-Turing論題猜想圖靈機不但可以用來討論現實中的可否計算性,還可以進一步將複雜度分析的結果延伸至物理世界中的計算。也就是說,如果$\textsf{P}\neq\textsf{NP}$,那麼在延伸版Church-Turing論題的保證下,也不會存在一個物理世界中的計算方式能夠快速地解決NP完備問題!
那專家們對於延伸版Church-Turing論題抱持著什麼樣的信念呢?不像原版的Church-Turing論題,理論電腦科學家普遍對於延伸版Church-Turing論題沒那麼有信心,甚至在一些量子演算法(下一章將會深入探討)被提出之後,很多人漸漸對延伸版Church-Turing論題抱持著懷疑。不過即使在古典力學的範疇內,延伸版Church-Turing論題可能就已經不是那麼有說服力了?
著名的華人理論電腦科學家、圖靈獎得主姚期智曾經就此撰寫過一篇論文『Classical Physics and the Church–Turing Thesis』,試圖以古典力學中的多體問題,喚起大家對延伸版Church-Turing論題的省思。
牛頓其中一個著名的力學成果,就是將只有兩個物體的力學系統,完全地用數學描述清楚。也就是說,給定(太空中)兩個物體的初始狀態和時間$T$,牛頓可以有個公式直接告訴你在時間$T$之後這兩個物體的位置和速度為何。然而,一旦現在有了三個物體,至今仍沒有人能給出類似的數學公式,這又被稱為三體問題。
同時,我們可以在實驗室中架設好環境,將物體們設置在初始狀態,並讓其自然演化長度$T$的時間,在觀測最後的結果。這樣容易做出來的實驗,不就輕鬆地幫我們解決了一個“計算問題”!?甚至在更開腦洞想下去,如果我們可以透過Cook-Levin定理和古典力學的關聯,將任何的計算問題都轉換成一個相對應的多體力學問題,那是不是就可以在物理實驗室中快速地計算任何問題了?這些充滿物理、計算、與哲學的問題,至今仍然沒有令人滿意的答案。
混沌、隨機性與偽隨機性
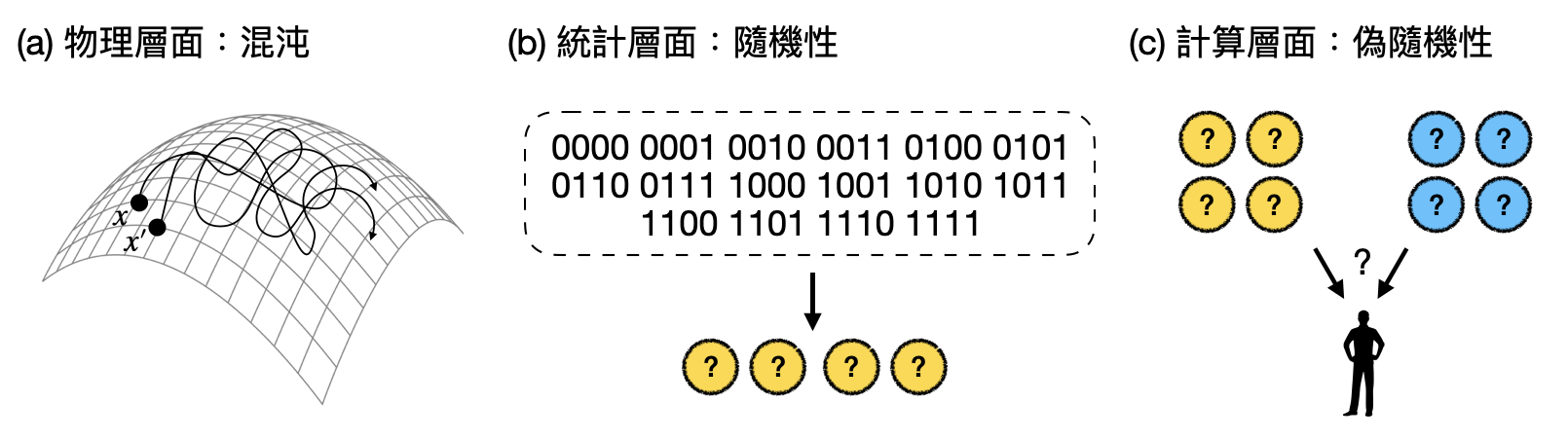
乍看之下,混沌似乎和隨機性息息相關:前者關乎物理演化過程中的難以預測性,後者則是著重在統計層面上的難以分辨性。另外一個相關的概念則是電腦科學中重要的偽隨機性(pseudorandomness),其考慮的課題是如何使用少量的隨機性產生出更多讓人無法和完美隨機性分辨的結果。
在目前理論研究的前緣,混沌仍是個具有一些公認物理特性,但缺乏乾淨數學定義的概念。某些混沌現象可以用統計上的完美隨機來近似刻畫。例如,路徑的平均和標準差(二次統計量)與完美隨機性的平均及標準差很接近。然而,“接近完美隨機性的平均及標準差”這個條件並不代表一個動力過程是混沌的。近年來在量子重力學的領域有些研究開始試著將混沌與計算理論中的偽隨機性作連結,也許透過計算模型的數學刻畫,可以幫助物理中的混沌現象找到新的數學定義?
拉格朗日力學與凸優化中的斜率下降演算法
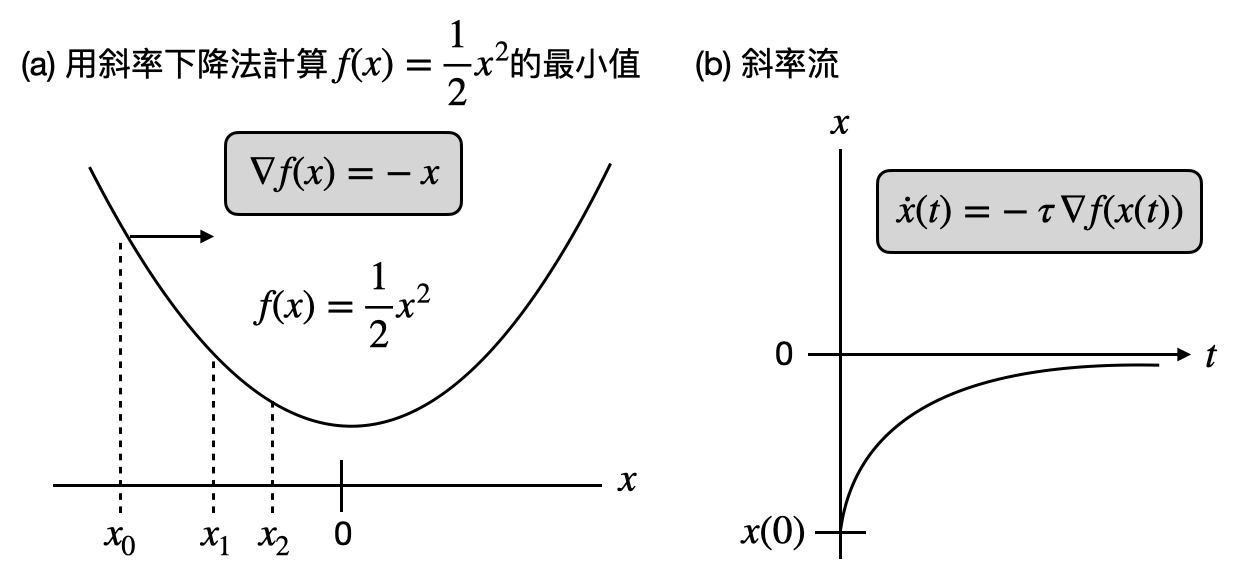
在第二章中,我們曾經提到凸優化問題並且宣稱它是個簡單的計算問題。而其中一個常見解凸優化問題的演算法是「斜率下降法(或稱梯度下降法, Gradient descent)」,其概念很容易用圖片解釋如下:
直覺上來說,想像你身在一個山谷,目標是要走到最低點,四周可能充滿了樹木讓你分不清方向,這時候你可以怎麼做呢?最簡單直接的辦法就是,跟隨當下所處地方的坡度來走,看哪個方向最傾斜向下,就往哪邊走!一旦這個山谷的地形夠友善(convex),不會有一個局部的小谷底(local minimum),那麼照著這樣做就一定可以讓你走到谷底。等等,這樣跟隨地心引力走的策略,聽起來是不是很有物理圖像呢?
讓我們把這個物理直覺和之前提到的拉格朗日力學做連結!假設我們要最小化一個函數$f(x)$,斜率下降法將會從一個起點$x_0$開始,然後在第$t$個時間點從$x_t$進展到$x_{t+1}=x_t-\tau\nabla f(x_t)$,其中$\nabla f(x)$是函數$f$在點$x$的斜率,$\tau>0$則是一個決定“步伐大小”的參數。如果將時間從離散變成是連續的,斜率下降法將會定義出一個路線函數$x(t)$,這個連續化的版本通常又被稱作「斜率流(gradient flow)」。在時間$t$瞬間,$x(t)$變動的方向為 \begin{equation*} \dot{x}(t)=-\tau\nabla f(x(t)) \, . \end{equation*} 以上由斜率下降法給出的路徑$x(t)$,將會是以下的Lagrangian系統,當把參數$m$逼近$0$時選擇走的路徑(也就是最小作用量路徑)! \begin{equation*} L(q,\dot{q},t) = e^{t/m}\left(\frac{1}{2}\dot{q}^2-\frac{\tau}{m}f(q)\right) \, . \end{equation*} 感興趣的讀者可以使用之前學到的Euler-Lagrange方程式來驗證一下。
這可不是巧合,一些其他斜率下降法的變形,也都可以被寫成某個Lagrangian系統的最小作用量路徑(感興趣的讀者請參考延伸閱讀)。這個連結更不只限定於古典力學,統計力學中的Langevin動力系統也和隨機版本的斜率下降法有深刻的連結,並且幫助機器學習研究者分析學習演算法的極限表現。原來不只物理可以被描述為優化問題,凸優化問題也能夠有很自然的物理圖像!
總結
古典力學帶給了世人一個機械性的世界觀:只要知道了一個物理系統的初始狀態及演化規則,就可以一步一步計算出系統未來的演化過程。這樣的視角不但開啟了近代物理學的蓬勃發展,也更是埋下了物理和計算之間糾葛關係的伏筆。
在本章中,我們首先從歷史的脈絡重新體悟牛頓力學的重要性。接著更進一步看到拉格朗日力學如何將牛頓的“動態”模型轉化為“靜態”的模型,使用最小作用量原理作為世界運行的公理,。從此,物理就和優化問題脫不了關係了。最後,我們看到幾個古典力學和“計算”在不同層面的連結,從重要的Cook-Levin定理和Church-Turing論題到偽隨機性與凸優化演算法。物理和計算互相提供靈感,相輔相成,這將會在未來幾個章節中不斷出現。
延伸閱讀
教科書與其他教材:
- J. R. Taylor. Classical Mechanics. Sausalito, Calif. :University Science Books, 2005.
- A. Deriglazov. Classical mechanics: Hamiltonian and Lagrangian Formalism. Springer International Publishing, 2016.
- J. Gleick. Chaos: Making a new science. Penguin, 2008.
內文中提及的論文:
- C. A. Yao. Classical physics and the Church–Turing thesis. Journal of the ACM, 2003.
- A. Wibisono, A. C. Wilson, and M. I. Jordan. A variational perspective on accelerated methods in optimization. Proceedings of the National Academy of Sciences, 2016.
科普書籍或小說:
- S. Weinberg. To Explain the World: The Discovery of Modern Science. Harper/HarperCollins, 2015.