$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



第7章

宇宙至暗處：重力理論



Black holes are where God divided by zero.

黑洞是上帝被除以零之處。

Albert Einstein


浩瀚的宇宙，一直是人類在科學與藝術上靈感的泉源。從哥白尼、克卜勒、伽利略到牛頓等人，透過了解星球運轉軌跡時，催生出古典力學理論以及之後輝煌的發展。當二十世紀初愛因斯坦創造出相對論後，這樣的榮景卻突然主客易位：相對論中的數學反過來暗示著宇宙遠比我們原本想像的還要豐富精彩。Schwarzschild在1916年預言的黑洞，超過一百年後才被天文學家“觀測”到。霍金在上個世紀後期預言的黑洞輻射，不知道在我們有生之年有沒有機會被實驗證實？

和直接感受與觀察物理世界很不一樣的是，如今這些“重力理論”被數學牽著走，因此許多預測在第一時間其實很違反直覺。如果想要“感受”這些物理直覺，那勢必要先建立一些相關的數學語言和架構。雖然會有一段長路要走，但可以確信的是，這將會是趟很有意思的旅程。

重力理論

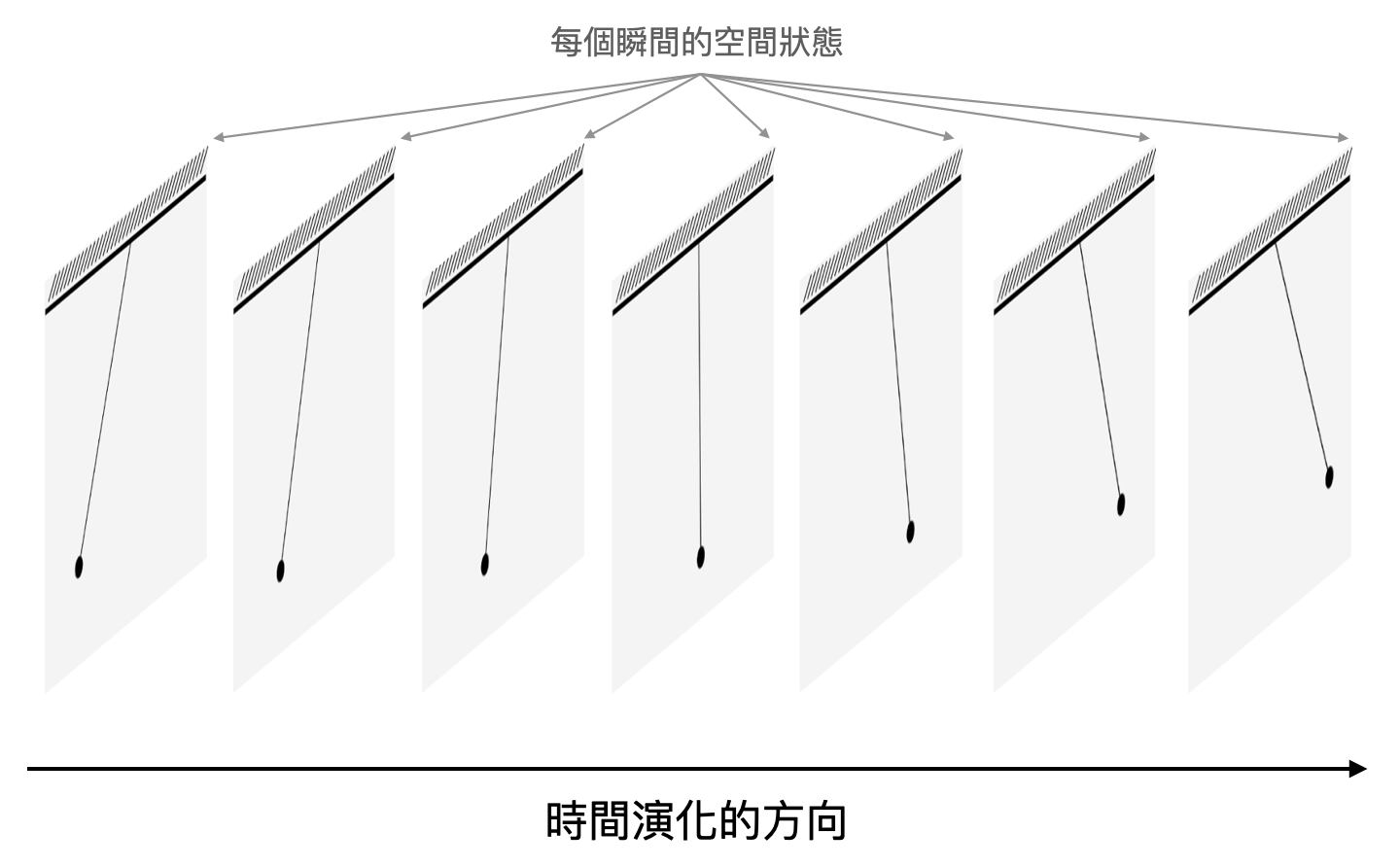
從牛頓(和伽利略)建立在三維歐式空間的世界觀、古典力學考慮的組態空間或相空間到量子理論中的希爾伯特空間，全部都是將想研究的物理系統，獨立描繪成一個客觀的(數學)世界。物理世界的運轉就像是切換一幀一幀的電影鏡頭，每一幀鏡頭都是世界在某個瞬間的剪影。而物理學家們就像是群看電影的觀眾，從旁觀的角度欣賞和講評電影中的高潮迭起。

不過等一下，物理學家和我們都是這個物理世界的一份子，沒有道理應該一直站在上帝視角看這些電影。如果我們走進電影的世界中，這些建立好的物理世界觀會有什麼改變呢？

走進電影世界中：重新思考時空的幾何

一旦失去了看電影的上帝視角，我們再也無法同時知道男女主角對彼此的愛慕之情，也無法來去自如地切換角色們在過去與未來的不同時刻。從物理上來說，在走進電影的那刻我們失去了一個重要的東西：時鐘。

假使某個遙遠的星系中也存在著文明，在你閱讀這段文字的當下，那邊的居民同時在做些什麼呢？在回答這個問題之前，如果宇宙沒有一個客觀的時鐘(或是你喜歡的話可以稱其為上帝的時鐘)，該怎麼定義什麼是“同時”？

從前我們站在螢幕外時，每一幀電影鏡頭都定義了一個“同時”的瞬間，從幾何的角度來看，就像是將無限多個三維歐式空間依照時間的方向疊在某個四維空間中(如下圖的降維版本)。如今我們身在電影之中，再也沒有一個客觀的時鐘，時間和空間共同背後共享的幾何會是什麼？

Minkowski時空與狹義相對論

「既然無法控制別人的想法，不如好好關心自己吧」，這不僅僅是句人生雞湯，也是「Minkowski時空(Minkowski spacetime)」的核心思想：與其糾結於如何定義一個適用於空間中所有點的共同時鐘，不如專注於描繪每個點各自身邊的時空演化。

Hermann Minkowski(1864-1909)是個英年早逝(在44歲時因為闌尾炎突然過世)的物理學家，愛因斯坦(Albert Einstein, 1879-1995)在蘇黎世聯邦理工學院求學時曾經上過許多他開授的課，或多或少促進了之後愛因斯坦在1905年提出的狹義相對論。Minkowski也在狹義相對論(special relativity)提出之後，從幾何的觀點用Minkowski時空重新詮釋狹義相對論，這個角度更是在愛因斯坦之後於1915年提出的的廣義相對論(general relativity)中扮演著重要的引路人。

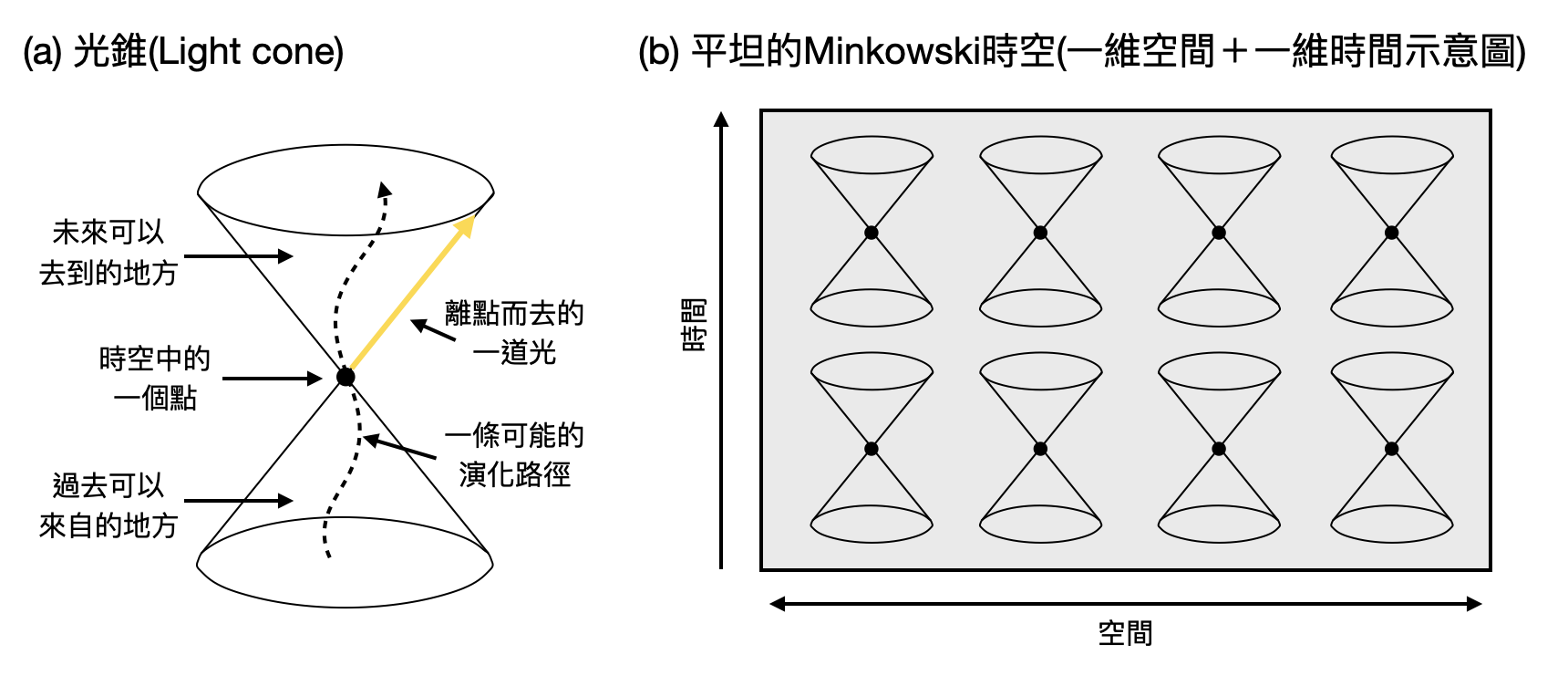
狹義相對論其中一個重要的公設是「光速有限且不變」(另一個是等效原理，由於之後將不會用到所以在這邊就暫時略過)。由於光承載了信息的傳遞，從時空幾何的角度，我們可以將這個公設理解為空間中每個點在有限的未來都只能看到周圍有限的空間，並稱這些能夠看見的未來(以及過去)為這個點的「光錐(light cone)」(如下圖(a))。

(a)由於在狹義相對論中假設了光速是有限的，於是時空中的一個點並不能任意的移動到另外一個點，我們可以將其能夠到達的點以及過去能夠到達它的點蒐集起來，並稱之為光錐。一個粒子在時空中的演化必須進行在光錐內。本圖以及未來的圖片都將三維空間簡化為二維空間以方便理解。本圖將空間與時間的尺度調整到讓(離點而去的)光速在光錐中會沿著45度角的方向前進。(b)狹義相對論對應到了平坦的Minkowski時空，在裡面每個點的光錐都是平行均勻地擺放著。

從Minkowski時空的觀點來重新解讀狹義相對論的世界觀，光錐將會均勻地擺放在時空中，並且使用所謂的「Lorentzian度量(Lorentzian metric)」來定義時空中的“距離”。如此一來，在電影世界中，時空的幾何決定了物體的移動與演化，物理學家們便可以方便地計算與討論物理觀測量的值(例如時間的流逝)以及事件的因果關係。

愛因斯坦場方程式與廣義相對論

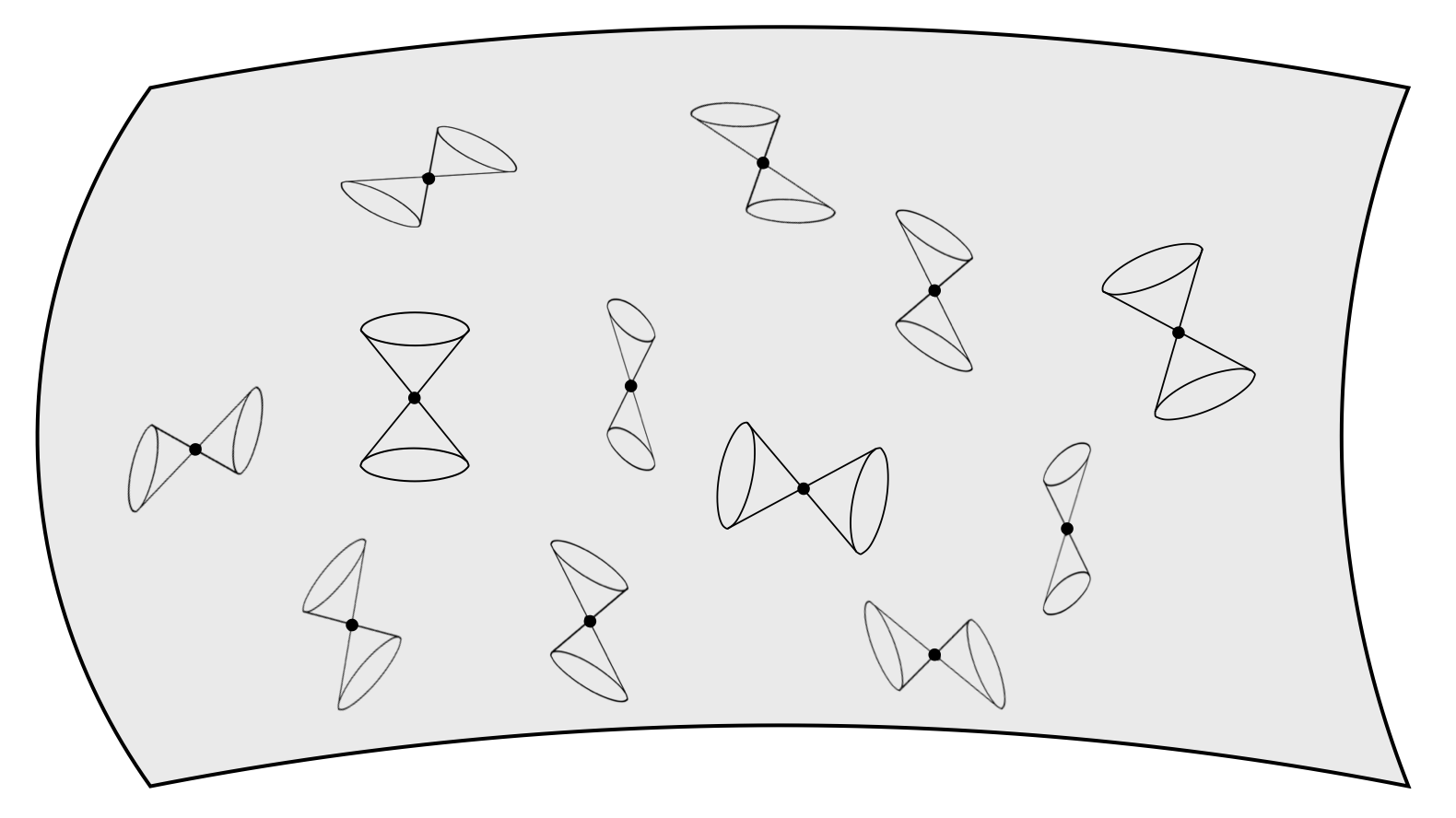
狹義相對論中的Minkowski時空，使用著一個“平坦的”Lorentzian度量。直覺上來說，就像是一張空白均勻的畫布。當我們開始加入一些東西到畫布上之後，其幾何形狀會保持一樣嗎？如果加入的東西非常重，畫布會不會凹陷下去？愛因斯坦在廣義相對論中告訴我們，沒錯，時空並不是平坦的，很重的物體可以扭曲時空的幾何！最震撼人心的是，愛因斯坦只用了一條公式就描述了時空幾何與物質之間的糾纏關係，這個重要的公式於是被稱為「愛因斯坦場方程式(Einstein field equations)」。

\begin{equation*} R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R=\frac{8\pi G}{c^4}T_{\mu\nu} \, . \end{equation*}

如果都讀到此處了，不多花個兩三分鐘試著一瞥愛因斯坦場方程式背後的含義，實在有點可惜。廢話不多說，就讓我們從“字面上”來感受愛因斯坦場方程式的氣魄與美麗。

首先，愛因斯坦場方程式中的變數“只有”四個：$R_{\mu\nu},R,g_{\mu,\nu},T_{\mu\nu}$，其他的符號都是宇宙中的常數($G$是重力常數、$c$是光速、$\pi$是圓周率)。在這四個變數中，身在左手邊的前三個($R_{\mu\nu},R,g_{\mu,\nu}$)對應到了時空的結構(例如幾何上的曲率、因果關係等等)，而身在右手邊的最後一個($T_{\mu\nu}$)則是對應到時空中物質的性質(例如密度、能量、通量、動量等等)。也就是說，愛因斯坦場方程式的確反映了之前提到的直覺圖像：

Space-time tells matter how to move; matter tells space-time how to curve.

時空告訴物質該如何移動，物質告訴時空該如何彎曲。

John Wheeler

在廣義相對論中，愛因斯坦場方程式中的時空度量g刻畫了時空的幾何，因此時空可以不再像平坦的Minkowski時空，尤其物質的性質可以影響時空彎曲的程度。

於是，當物理學家說要“解”愛因斯坦場方程式，意思是要找到一組具體的($R_{\mu\nu},R,g_{\mu,\nu},T_{\mu\nu}$)並滿足方程式中的等式。

最後，必須承認之前偷偷隱瞞了讀者，其實愛因斯坦場方程式不只有一條公式，$R_{\mu\nu},g_{\mu,\nu},T_{\mu\nu}$下標中的$\mu$和$\nu$各自有四個軸向(一個時間軸，三個空間軸)，因此愛因斯坦場方程式其實對應到了16條公式！此外，$R_{\mu\nu},R$和$g_{\mu\nu}$是由某些非線性偏微分方程式所牽制住。因此，找出一個愛因斯坦場方程式的解是件非常不簡單的事情！整個廣義相對論的研究可以說就是在尋找和分析各式各樣愛因斯坦場方程式的解，有興趣的讀者歡迎參考延伸閱讀中推薦的教科書。

Schwarzschild與黑洞

愛因斯坦當年提出愛因斯坦場方程式時，其實並沒有找到一個解。他甚至一度懷疑需要很多年後才會有人能找出一個解，畢竟光是解一條非線性偏微分方程就夠頭疼了，現在竟然要一次要解16條！

沒想到，愛因斯坦發表廣義相對論沒過幾個月後，還正在第一次世界大戰前線戰鬥的天文學家Schwarzschild(Karl Schwarzschild, 1873-1916)，就透過書信在1916年初發表了第一個愛因斯坦場方程式的解。為了紀念他的貢獻，後人將這個解稱為「Schwarzschild解」。然而另人難過的是，同年五月Schwarzschild就死於戰火的煙硝中了。

就像理論電腦科學家相信$\textsf{P}\neq\textsf{NP}$，還沒看到Schwarzschild解之前，大家都覺得解愛因斯坦場方程式太困難了，但是一看到Schwarzschild給出簡單又乾淨的式子，就連一般人都能略品其精妙。在這邊讓我們暫且省略一些細節，從Schwarzschild解的時空度量$g_{\mu\nu}$感受彎曲的時空： \begin{equation*} g_{\mu\nu} = \begin{pmatrix}1-\frac{2GM}{r}&0&0&0\\
0&-\frac{1}{1-\frac{2GM}{r}}&0&0\\
0&0&-r^2&0\\
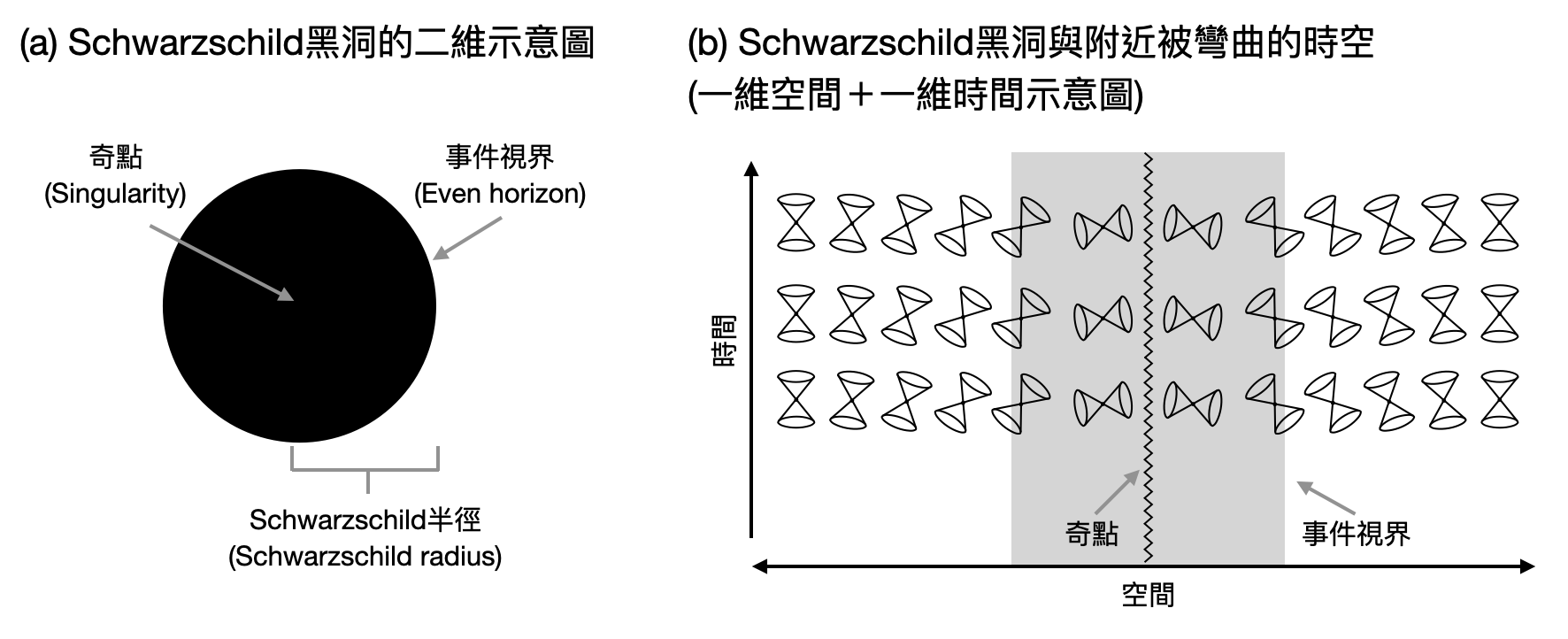
0&0&0&-r^2\sin^2\theta \end{pmatrix} \end{equation*} 其中$r$和$\theta$是空間極坐標的參量，$r$對應到了離某個質量為$M$的物質的距離。即使是在沒有更多背景知識的情況之下，我們就已經能夠從以下兩個觀察中，在數字上感受到Schwarzschild解的物理圖像：黑洞(black hole)。

(a)在黑洞的簡化圖像中，有三個重要的性質：(i)事件視界，一旦任何物體進入事件視界之後，引力將會大到無法讓其離開。(ii)黑洞中心的奇點，在此處的引力在數學上發散到無窮大，至今物理學家仍尚未釐清奇點可能的物理圖像。(iii)Schwarzschild半徑，是奇點到事件視界的距離。(b)透過之前學到的Minkowski時空及光錐來視覺化黑洞附近的引力變化，可以看到引力越大光錐會越傾斜，並在跨越事件視界的時候超過45度角。

通往大一統理論之路：量子重力

量子力學(以及其進階版本，量子場論)描繪了極度微觀世界的模型，廣義相對論(或是更廣義來說重力理論)則建立了極度宏觀世界的架構。對於追求美感的物理學家來說，一個再自然不過的問題就是：是否有個大一統理論能夠同時整合這兩個理論？走到這個夢想中的大一統理論之前，一個必經之路就是「量子重力(quantum gravity)」。

顧名思義，量子重力就是將量子世界與重力世界整合的理論，不過目前為止仍然還沒有一個公認的量子重力理論。更明確地來說，理論物理學家們從過去的經驗中，知道量子重力“應該”具有某些性質，然而不像其他的物理理論(例如古典物理有拉格朗日的最小作用力原理、統計物理有Boltzmann分佈、量子力學有薛丁格方程式、廣義相對論有愛因斯坦場方程式)，量子重力的世界觀尚未建立完成。

於是，在探索量子重力的路上，理論物理學家們便開始嘗試各種小模型來找尋靈感以及建立更好的物理直覺。黑洞身為愛因斯坦場方程式的特殊解(除了Schwarzchild解之外還有許多不同形式的黑洞解)，便理所當然的成為大型練武場。在剩餘的篇幅中，我們將看到兩個近年在量子重力研究中黑洞與計算相關的故事。

黑洞與計算複雜度

珍奶都可以做到pizza上面了，這樣相比起來，計算複雜度能在黑洞的研究中參上一腳，似乎也沒有太令人意外？不過，這兩者之間的連結可不是像珍奶愛好者看到什麼就把珍珠放上去，我們需要從目前為止建立的背景知識下，沿著歷史的發展繼續往前走。

霍金輻射(Hawking radiation)

霍金(Stephen Hawking, 1942-2018)也許是二十一世紀初期最廣為人知的理論物理學家，其科普著作(例如『時間簡史』等)將許多複雜的物理概念與理論用淺顯的故事或比喻深植人心，吸引了無數年輕心靈嚮往浩瀚的時空。除此之外，他在量子重力探尋之路的早期更是有著極為重要的貢獻：「霍金輻射(Hawking radiation)」。

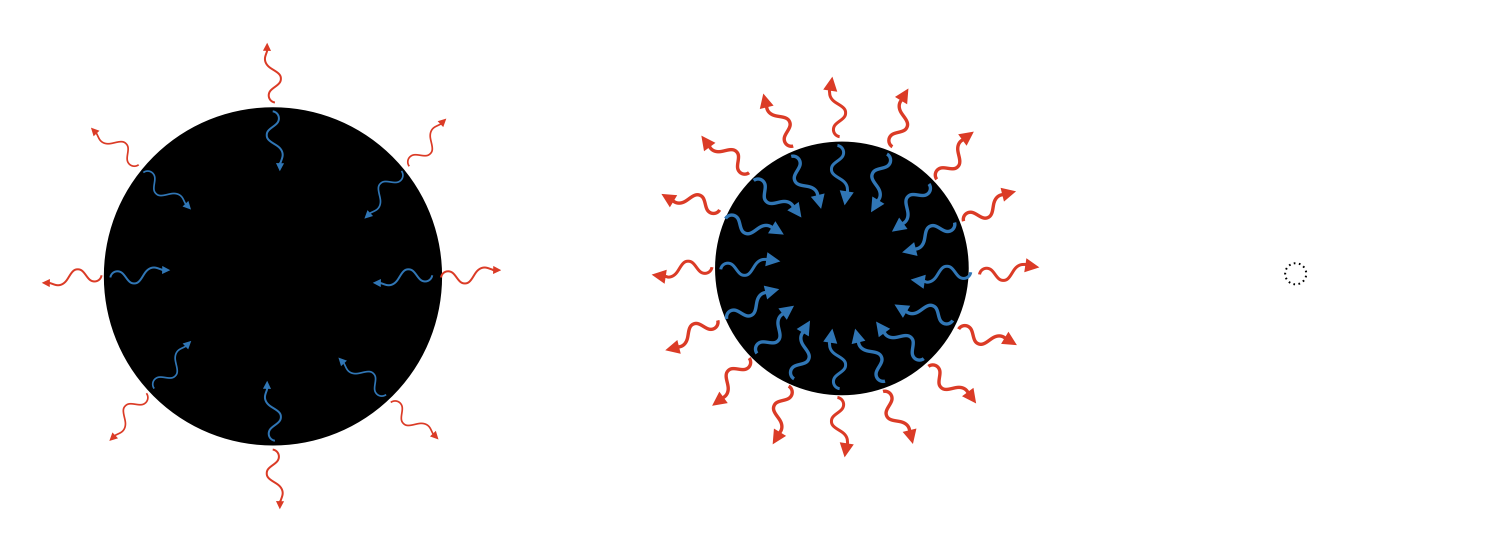
在物理學中，著名的黑體輻射(black-body radiation)告訴我們就算是再怎麼黑的物體，只要溫度不是絕對零度，仍然會產生輻射。而物理學家們普遍認為黑洞具有非零的溫度，甚至還可能蠻燙的！這代表黑洞也會向外輻射嗎？如果會的話，有沒有違反了事件視界不能讓物質返回的原則(除非超光速)？

在1974年，霍金直接用數學論證將證據擺在眾人面前：當在黑洞中考慮了量子效應，那麼其內部能量將會隨著時間減少，事件視界的半徑也會漸漸縮小。同時，黑洞會向外輻射！

霍金將量子場論用半古典計算引入黑洞中，發現黑洞會以某種方式向外輻射，並且不斷縮小。輻射的速率會和Schwarzschild半徑成反比，也就是越小的時候輻射速率越快。當黑洞只剩下奇點時，目前對於會發生什麼事情尚未有共識。

霍金是如何在黑洞中討論量子效應的呢？他使用了所謂的「半古典(semiclassical)分析」： \begin{equation*} R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R=\frac{8\pi G}{c^4}\langle\hat{T}_{\mu\nu}\rangle \, . \end{equation*} 也就是考慮量子化的物質場(在式子右邊將原本的$T$變成量子算符)，但是維持時空的古典性(式子左邊保持原樣)，並且在愛因斯坦場方程式中將量子的物質場取期望值使得兩邊形式相同。霍金只考慮半古典分析的主要原因是，當我們將時空放在一起討論時，該如何量子化就變得沒有那麼直接，有些不同數學形式的選擇以及許多數學計算的困難。

黑洞阻止了任何物質的逃脫，同時卻又以霍金輻射向外發出能量。這兩個現象之間聽起來怎麼好像有點相互矛盾？具體來說，之前章節出現過的“熵”出事了！

信息悖論(Information paradox)

根據天文學家的估計，和太陽差不多大的黑洞大約具有$10^{60}$的熵，在銀河系中央的黑洞則大約具有$10^{88}$的熵，而目前所知最大的黑洞則約有$10^{96}$的熵。簡單做個比較，天文學家估計整個宇宙的原子數量大約在$10^{80}$的層級附近。乍看之下，黑洞實在是個巨大的信息儲存器呢！

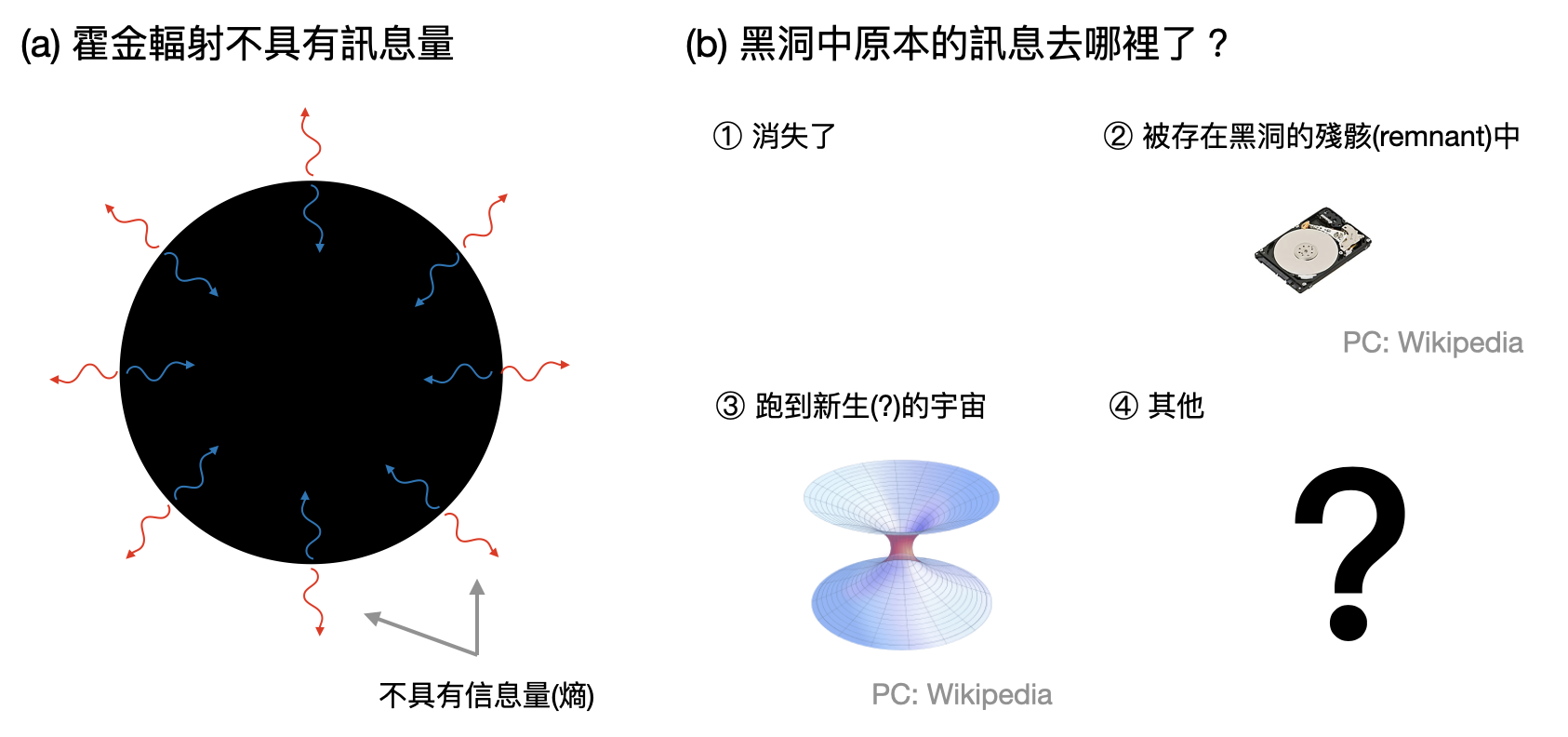
不過，霍金推導出來的輻射乍看之下是一種“熱輻射(thermal radiation)”，從傳統熱力學的角度來看，熱輻射最大的特性就是不含任何信息。當這些熵如此之高的黑洞蒸發完畢後(雖然要花很久的時間，以太陽大小的黑洞來說約要$10^{67}$年)，裡面的信息消失了嗎？如果是的話，消失到哪裡去了？

信息悖論：根據霍金輻射，蒸發完的黑洞看似流失其所有的熵值，於是黑洞中原本的信息憑空消失。

同時，在傳統的物理價值體系中，即使是在量子的世界中，一個封閉系統的信息量是會保持不會的。想像你在做麵包時偷偷在麵粉中加了一些珍貴的金粉，在麵團揉捏的過程中，這一小撮金粉將會和大量的麵粉、水和酵母混合。然而只要你有足夠的時間和心力，在原則上是可以從麵糰中分離出一開始加入的金粉，也就是說金粉這個“信息”並不會憑空消失！

霍金的半古典計算錯了嗎？還是黑洞在蒸發結束的瞬間會有什麼未知的事情發生？又或是黑洞與量子世界的接軌並沒有這麼單純？與其説信息悖論是個邏輯上的悖論，倒不如將它想成是量子重力理論的引路人？

(a)乍看之下霍金輻射似乎不包含任何信息量，因此理論物理學家們便開始思考黑洞事件視界中原本巨大的熵去哪了，這個問題又被稱為信息悖論。(b)人們對於黑洞中原本的信息去哪有幾個不同的猜測。有人覺得黑洞和一般物理系統很不一樣，不一定具有信息守恆的性質，所以信息有可能就這樣憑空消失了。也有一派說法覺得當黑洞蒸發完後，所有信息會被保留在奇點，成為一個極度稠密的殘骸(remnant)。另外也有些科幻的提議，例如信息跑到了其他的新生宇宙。

黑洞互補性

也許黑洞在本質上和我們日常習慣的物理系統實在太不一樣了，所以信息是可能憑空消失的？因為研究電弱交互作用的量子結構獲得諾貝爾物理學獎的Gerard ‘t Hooft，和著有多本暢銷科普書的弦論(以及量子場論等等)學家Leonard Susskind，是兩位堅信信息量應該守恆的理論物理學家，從信息悖論被提出以來，不斷努力嘗試各種方式要將看似消失的信息“找回來”。從’t Hooft早期提出的S-矩陣(S-matrix)到Susskind天外飛來一筆的「黑洞互補性(Black Hole Complementarity)」。經過將近三十年來和霍金陣營(認為信息在霍金輻射時消失了)之間的“戰爭”，現在專家們終於漸漸傾向接受黑洞中的總信息量還是以某種方式與霍金輻射和平共存。感興趣更深入了解這段故事的讀者，筆者在這邊推薦閱讀Susskind在2008年出版的科普著作『The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics』。

在這邊我們將不會深入戰事，而是只著重在Susskind陣營中關鍵的反攻號角：黑洞互補性。在講解之前，可以先讓我們短暫跳到結論以免之後迷失在細節：雖然目前來說大家仍對黑洞互補性是否提供了真實的圖像存疑，不過它激起的漣漪引發了眾多對黑洞信息悖論的深刻討論，並且催生了之後要提到的火牆悖論與黑洞和計算複雜度的關聯。

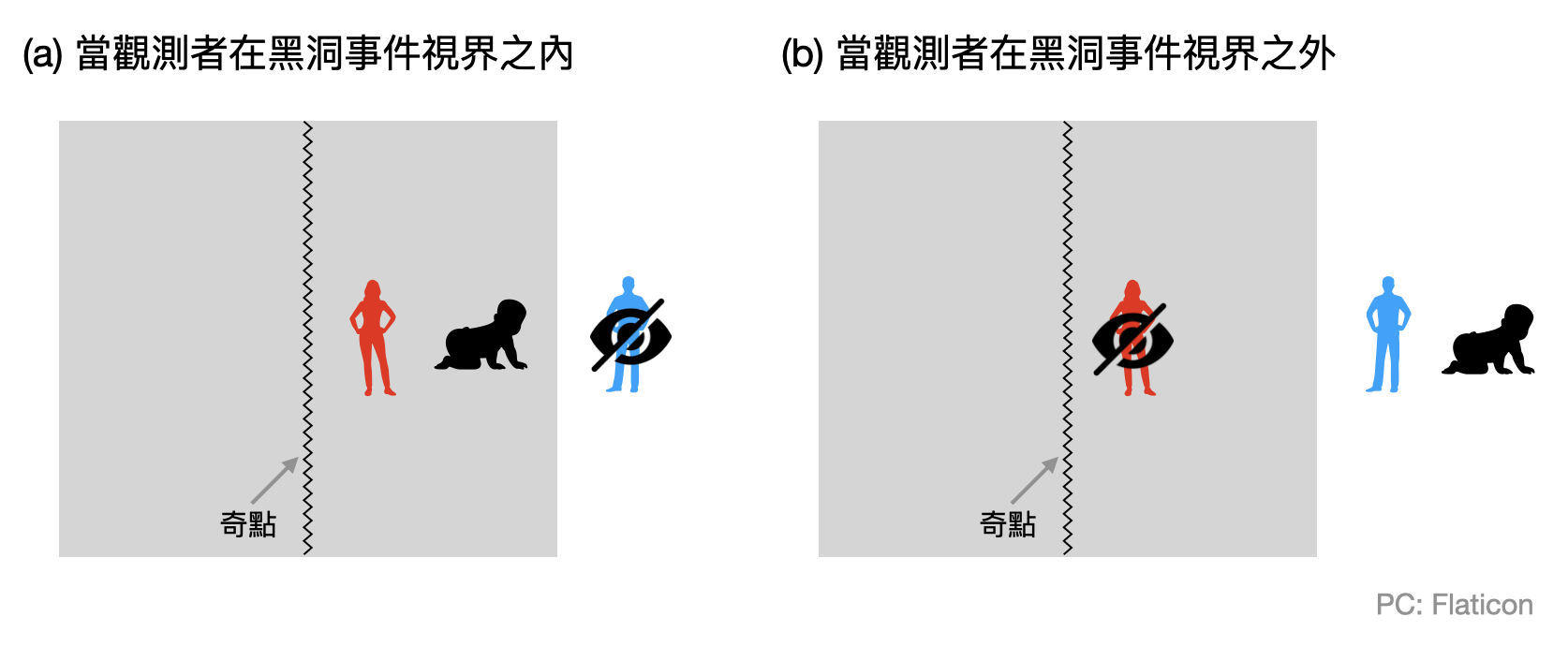
Susskind與合作者觀察到在信息悖論的一些具體數學版本中，都默認黑洞內外的世界處在同一個希爾伯特空間中，也就是說整個黑洞和其事件視界外的系統可以共同被一個量子態描述。而這個隱形的假設，正恰恰是在數學上可以被用來推導出矛盾的關鍵。於是Susskind大膽地提議：也許黑洞內和黑洞外是兩個世界(也就是兩個獨立的希爾伯特空間)，不可能有一個觀測者能夠同時觀察到兩邊的狀態！如同在量子力學中Heisenberg和Bohr告訴我們不能同時準確的測到粒子的動量和位置，並稱之為互補性，在黑洞事件視界的兩側，也許我們並不能同時觀測到兩邊，這，就是黑洞互補性。

信息悖論的設定中將黑洞內外的世界用同一個希爾伯特空間描述。黑洞互補性理論則猜測黑洞事件視界內外是兩個獨立的希爾伯特空間(圖(a)和圖(b))，觀測者並不能同時描述這兩個空間。

火牆悖論

2012年的夏天，來自美國加州Santa Barbara的四位理論物理學家Ahmed Almheiri, Donald Marolf, Joseph Polchinski, James Sully在網路上放了一份只有二十出頭頁的論文，名為『黑洞：互補還是火牆？(Black Holes: Complementarity or Firewalls?)』。他們提出了一個新的思想實驗，並且在一系列的邏輯推演之後說道：如果霍金輻射符合量子理論中的么正演化，而且同時如果黑洞互補性也是對的，那麼最有可能的情況就是黑洞邊界應該會有個「火牆(firwall)」將穿越黑洞視界的觀測者燒死。由於大部份物理學家是絕對不會相信這樣的火牆會出現在黑洞視界上面(基於對愛因斯坦「等效原理」的信仰)，因此，這個思想實驗得名「火牆悖論(Firewall paradox)」。以下讓我們用個簡化版的小故事讓讀者感受一下火牆悖論中邏輯的糾纏：

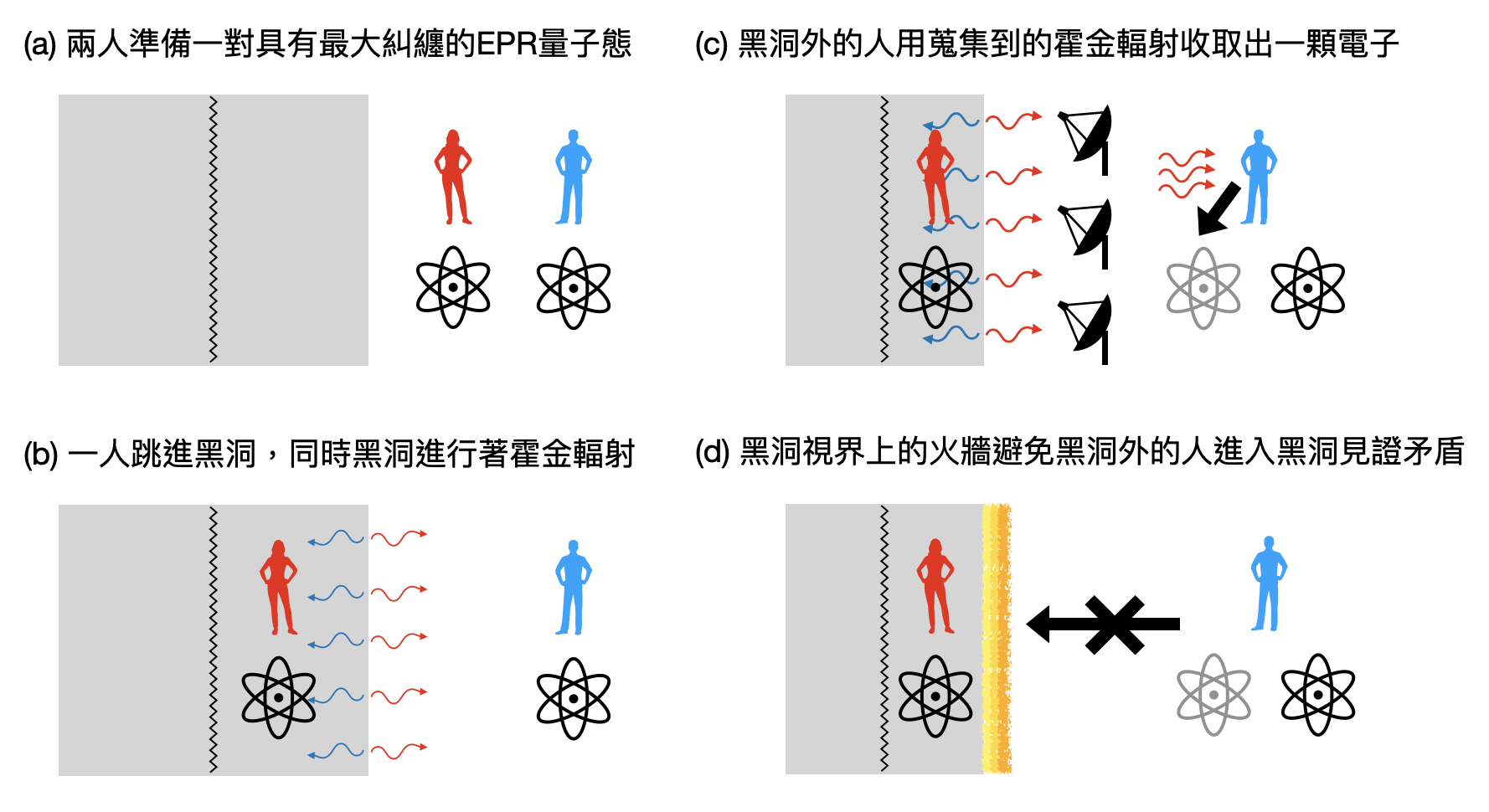
想像你在黑洞事件視界外和你的情人分別，在離別之際，你們將一對EPR量子態(最大的糾纏態)的兩個電子各取一個，並封印在你們的戒指上。接著你的情人便頭也不回地進入黑洞中。滄海桑田，黑洞也有蒸發的一天，如果黑洞的演化和蒸發是么正的話，那麼總有一天你的情人和她戒指上的電子也會以某種方式被輻射出來。從黑洞的斷簡殘瓦中，你在理論上可以萃取出屬於她的那顆電子，雖然無法再次相遇，曾經分離的電子卻可以重新強烈地相互糾纏著。然而對於進入黑洞的她來說，她和戒指上的電子都已經踏上了一條不歸路。即便時間流逝，在黑洞內部的她並不會感受到黑洞輻射的影響，畢竟根據黑洞互補性，輻射是事件視界外的人才能觀測到的事情。

(a)在這個思想實驗中，兩個人準備了一對具有最大糾纏的EPR量子態，並各取一個其中的電子。(b)接著其中一人進入黑洞的事件視界，同時黑洞進行霍金輻射。(c)在黑洞外的人用儀器搜集所有的霍金輻射，經過足夠久的時間之後，所搜集到的霍金輻射將足以讓黑洞外的人萃取出ㄧ個和他原本手中電子具有強烈量子糾纏的新電子。(d)如果黑洞外的人可以拿著原本的電子和新的電子跳入黑洞和裡面的人會合，那將會見證糾纏態一夫一妻制的矛盾。於是AMPS提議在黑洞外會有個火牆將試圖進去的觀測者燒死。

現在假設你從霍金輻射中萃取出情人的那顆電子之後，突然決定跳入黑洞。破鏡重圓之際，你戒指上的電子將會同時與你萃取出的電子、以及情人戒指上的電子達到極大的量子糾纏。但在同時，根據量子物理中的么正演化規則，將會推導出所謂的「糾纏態一夫一妻制(monogamy of entanglement)」，也就是一顆電子不能同時和另外兩顆電子最大的糾纏著。

於是，這邊就出現邏輯的矛盾了！一旦觀測者(你)可以自由地穿越事件視界進入黑洞內的希爾伯特空間，就算這在黑洞互補性的觀點下合情合理，但是將會與量子物理中的基礎原理產生矛盾。於是，AMPS(火牆論文四位作者的姓名縮寫)長嘆一聲表示，他們覺得最保守的猜測就是黑洞視界上會有個火牆，把試圖跑進去和情人會合的你燒死！

上述的思想實驗雖然提供了比較直覺的圖像，然而在嚴謹的物理討論中將會需要把故事中的一些時間尺度和實際糾纏情況等等講清楚，例如在原始的“火牆論文”中，AMPS使用了有關黑洞蒸發速率的「Page時間(Page time)」等進階概念，感興趣的讀者歡迎參考延伸閱讀中更嚴謹的版本。

Harlow-Hayden解碼問題與計算複雜度

火牆悖論ㄧ上市，就立刻引起領域內一陣騷動，各方陣營馬上拿出渾身解術，試著尋找邏輯中的漏洞或是修補黑洞互補性，盛況堪比當年由信息悖論引起的第一波戰火。隔年一月，Daniel Harlow和Patrick Hayden的一篇論文，將看似不相干的計算複雜度理論拉入了混戰之中。

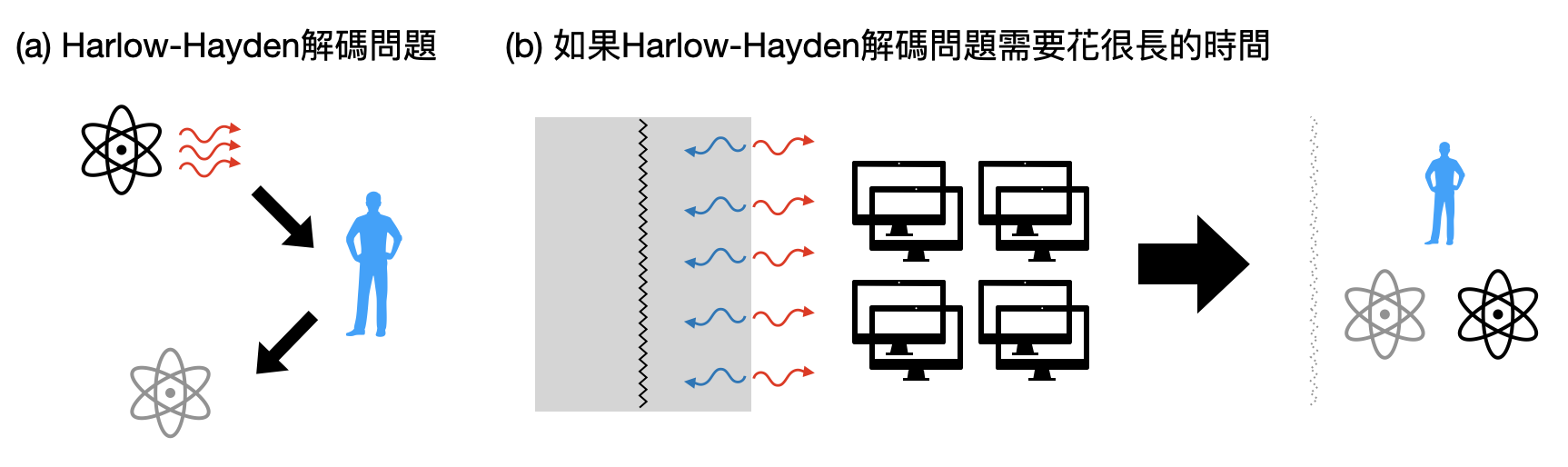
Harlow和Hayden將火牆悖論中的思想實驗，想成了一個量子計算問題：身在黑洞外的你，想要從霍金輻射中萃取出進入黑洞的電子，如此一來才能拿著這顆電子跳進去和情人會合。這時候Harlow和Hayden很煞風景地問説：如果從霍金輻射中萃取出電子需要花很多時間，甚至比黑洞完全蒸發的時間還要久，那你是不是就來不及跳進黑洞見證“糾纏態一夫一妻制”的矛盾了呢？

更進一步來說，如果將黑洞想成一個巨大的量子攪拌器(具體來說學者們考慮了隨機量子線路，或是量子單向函數等等)，會將所有進去黑洞的東西都混在一起，然後再透過霍金輻射緩慢地釋放出部份的信息。身在黑洞外的你，如果可以透過儀器錄製所有已經出來的霍金輻射，倒底能夠多迅速地從被攪混的殘骸中萃取出那顆珍貴的電子？這樣的一個計算過程又被稱為「Harlow-Hayden解碼問題」。

由於火牆是個不太合理的存在，物理學家們便開始思考有沒有其他的可能。(a)Harlow與Hayden首先將上圖(c)中，黑洞外的人萃取新電子的過程描繪成一個計算問題，又被稱為Harlow-Hayden解碼問題。(b)接著，他們利用計算理論的技術，試圖解釋Harlow-Hayden解碼問題在一些常見的計算複雜度假設之下，會需要花很多時間才能夠達成。因此，當黑洞外的人萃取出新的電子時，可能黑洞早就蒸發完畢了。

於是，一個潛在能夠排除火牆悖論的論述便出現了：如果黑洞像是個密碼學中的單向函數(曾在本書第三章中出現)，那麼計算複雜度中類似於“P vs. NP”的困難度假設，便可以用來提供證據顯示Harlow-Hayden解碼問題在現實中可能無法在黑洞完全蒸發之前完成，於是身在黑洞外的你，將不會有足夠的時間萃取出電子，並進入黑洞見證矛盾。

火牆究竟是否存在於事件視界上？信息是如何遊蕩在黑洞兩側？黑洞互補性是不是物理世界中的本質原則？現在似乎還沒到了能夠下定論的時間。與其說Harlow與Hayden用理論電腦科學家對困難問題的漸進式信仰，在黑洞的論爭中滅火，回頭看看，這個連結也許更像是給了兩個不同的理論領域一個認識彼此的窗口。未來將會擦出什麼樣的火花，值得令人期待。

黑洞與量子糾錯碼

在市場買水果的時候，有經驗的婆婆媽媽們總是能透過觀察水果的表面、聞一聞氣味，就判斷出這顆蘋果或是那顆西瓜甜不甜。理論物理界近25年來引用數目最高的論文，竟然和此有異曲同工之妙！？在本章的最後一個主題中，我們將看到電腦科學中的“錯誤糾正(error correction)”如何在黑洞研究的前線提供彈藥。

AdS/CFT對偶

來自阿根廷的Juan Maldacena，是位具有一雙深邃棕色眼睛的理論物理學家。在那無懼眼神的背後，是許多人夢寐以求的犀利物理直覺。在1997年當眾人還在霍金蒸發的泥沼中摸索量子重力學的方向時，Maldacena如同哥倫布發現新大陸一般，直接畫出了一幅新世界的地圖：AdS/CFT對偶(AdS/CFT correspondence)。

Maldacena的想法有點像是個進階版的婆婆媽媽水果甜度判別法，他先將某種類型的重力時空(AdS)描述為水果的內部，再把某個量子理論(CFT)作為水果的表皮，並寫下一連串表皮資訊和內部性質的對應關係。例如香氣對應到甜度和軟硬對應到成熟度等等。不過，就像婆婆媽媽的方法尚未有嚴謹的科學根據，Maldacena最初的AdS/CFT對偶也像是一張工程藍圖或一本字典，於是讓理論物理學家們在之後的幾十年有工作可以試著把其中的一些對應關係在數學和物理上嚴格化。

AdS/CFT對偶是個極度複雜深刻的理論，需要多年的學習才有機會自如地遊走於兩個世界之間。以下我們將提供一些過度簡化的圖像直覺，一來希望讓非專業出生的人(包括筆者本人)能建立基本概念，幫助理解之後和“錯誤糾正”的關聯。二來希望激起一些讀者的興趣，之後可以再進一步鑽研延伸閱讀的內容。

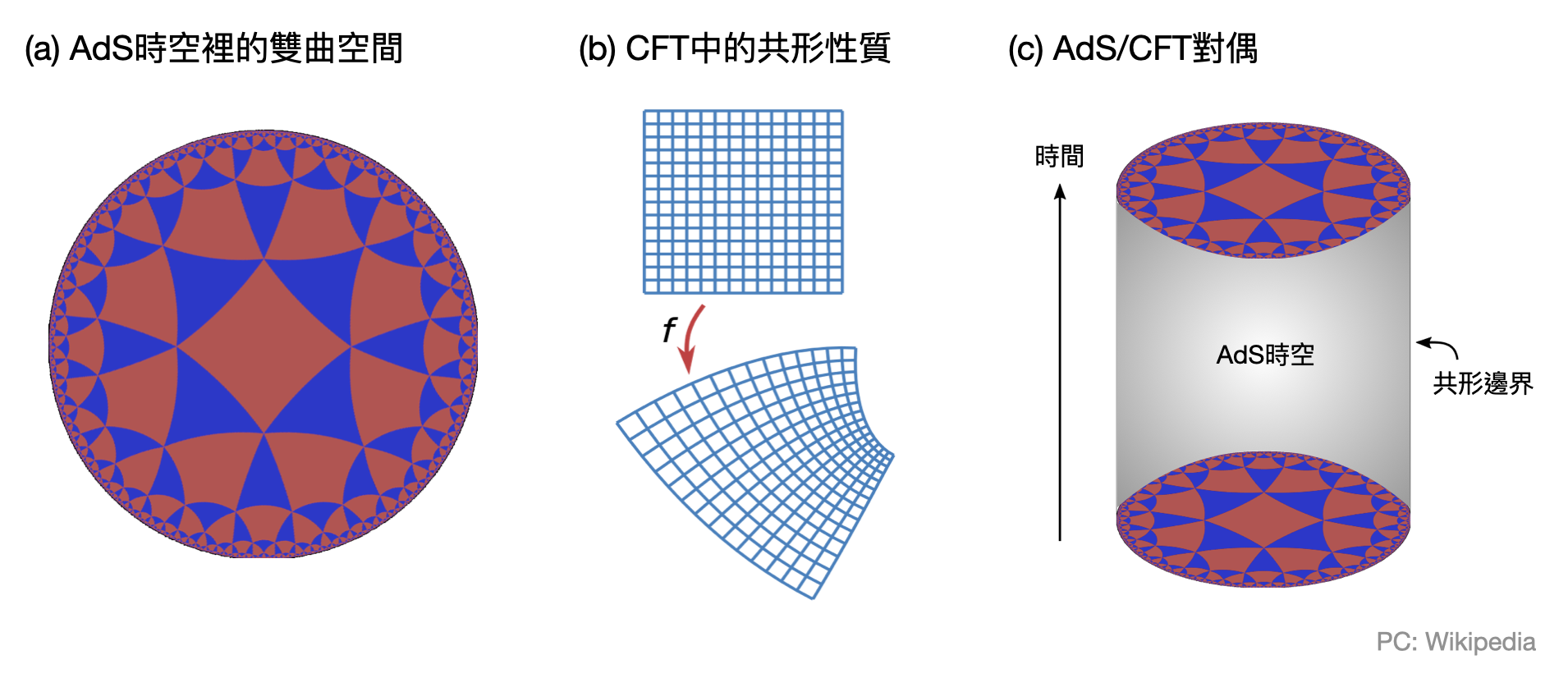
Anti-de Sitter時空(AdS, Anti-de Sitter space)指的是愛因斯坦場方程式中，一類特殊的時空解。AdS宇宙中的真空能量是負的，造成其內部空間幾何是雙曲的，因此不會像我們所處的宇宙一樣會不斷擴張(如下圖(a))。

共形場論(CFT, Conformal Field Theory)指的是一種特殊的量子理論，其特性是在「共形轉換(conformal transformation, 或稱保角轉換)」下會維持觀測量的不變。這個性質也讓共形場論具有「量子態-算符對應(state-operator correspondence)」，讓我們可以透過一些主要算符(primary operators)的算出各個(內部)點對應的局部算符。

基於上述AdS和CFT類似的數學性質，Maldacena提議將一個AdS時空的邊界用一個(低一個維度的)CFT來描述(如下圖(c))。

(a)AdS時空的幾何具有雙曲結構，本圖呈現二維版本的示意圖。一個和我們所處的宇宙很不一樣的性質是，在AdS空間中，當你向外發射一到光的時候，將會在有限的時間之內就看到這道光抵達無窮遠的地方。(b)CFT中的性質將會在共形轉換下被保持不變。共形轉換又稱保角轉換，顧名思義，就是指空間中兩條直線間的角度在轉換後仍維持一樣。例如本圖中直線之間的角度在轉換前和轉換後都是90度。(c)一個將2+1維(2維空間+1維時間)的AdS空間對應到2維CFT的示意圖。

表面重構與AdS/Rindler謎題

在完善AdS/CFT對偶的路途中，很重要的一步是「表面重構(bulk reconstruction)」。想像你要買的水果是顆巨無霸西瓜，直接對整個西瓜表面做觀察太麻煩了，於是你只能一次在某個小塊的表皮上做實驗，然後根據幾次實驗(可能在不同位置表皮)的結果，來推測巨無霸西瓜的內部性質。這樣雖然可能無法得知西瓜內部的所有資訊，但如果你只想知道某個內部小區域是不是甜的，能夠透過這些在表面上有限制的實驗做到嗎？

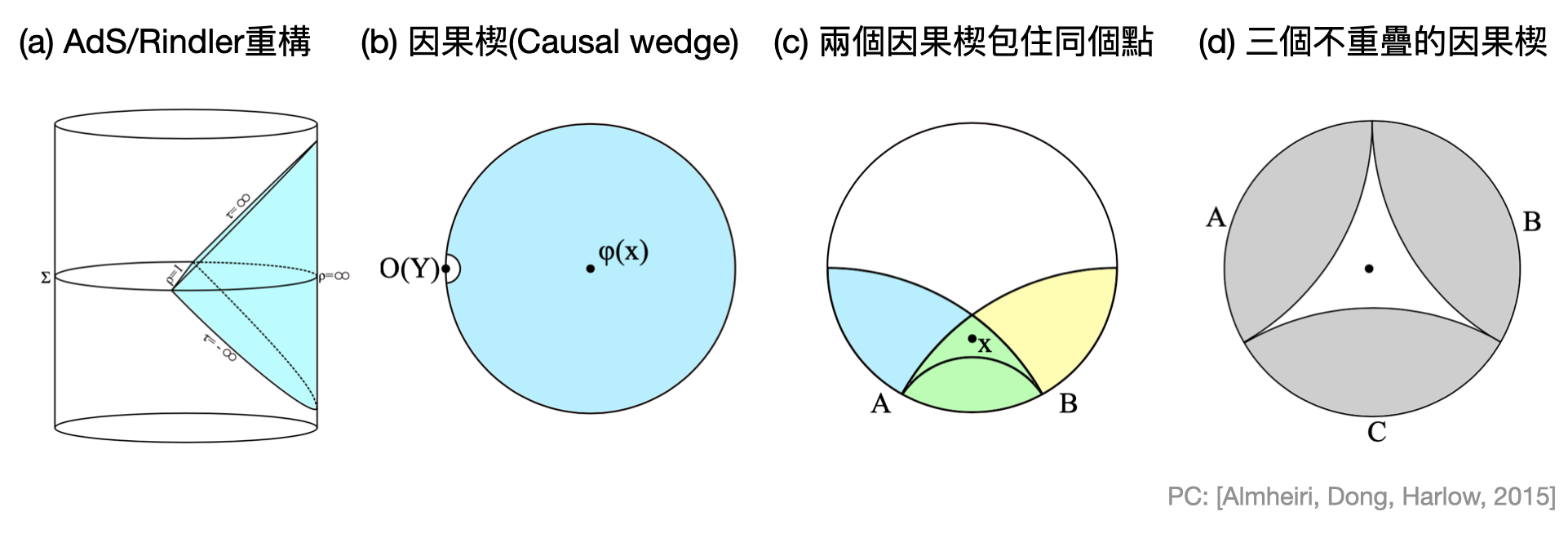
在AdS/CFT中，答案是正面的：「AdS/Rindler重構理論」告訴當我們停在一個時間點，並且想要研究AdS時空內部的點時，一旦這個點落在觀測表面的「因果楔(causal wedge)」中，那就可以經由表面測量到的資訊重構這個點的一些性質！這樣只需要局部表面就能重構的性質在AdS/CFT中又被稱為「內部局部性(bulk locality)」。這邊提到的因果楔有點類似之前在Minkowski時空出現的光錐，不過實際的定義需要多知道一些相關背景知識，所以在這邊我們將只用下圖來提供圖像直覺。

(a)圖中藍色區域又被稱為一個Rindler楔(Rindler wedge)，一旦知道其表面的CFT資訊，就可以用來重構內部某個點的性質。(b)讓我們專注在一個固定的時間切片(又稱Cauchy切片)上，其和Rindler楔的交集被稱為因果楔。只要知道一個因果楔邊界的CFT資訊，就可以用來重構因果楔內AdS空間中一個點的性質(例如圖中的x)。(c)如果現在考慮比較小塊的因果楔，可能會出現圖中的情況：A和B兩個因果楔都包含了點x，但是A和B相交後的邊界再定義出來的因果楔將不會包含x。如此一來，因果楔A和B到底是描述了x什麼樣的性質呢？(d)如果AdS中的點x比較接近中心的話，甚至可能出現許多因果楔互不相交，又不包含x的情況。這些特殊情況當時另一些物理學家不知道該如何理解Rindler重構出來的資訊。

從上圖中(例如圖(b))我們可以發現一個內部的點可以同時在許多不同的因果楔裡面，因此，對於任何一個包住它的因果楔，其表面都將具有足夠的資訊可以告訴我們一些關於這個點的性質。乍看之下，CFT用了一種非常容錯的方式在表面紀錄AdS內部的資訊，這樣聽起來不是很棒嗎！？

但別忘了，我們現在想吃的是一顆巨無霸“量子”西瓜，有許多奇怪的限制會違反原先的物理直覺！類似於在第6章提到的不可複製定理，在AdS/Rindler重構理論中的「時間切片公設(time slice axiom)」將會要求不同的因果楔對於同一個被包含住的內部點，有不一樣的重構結果(正確的來說，是不一樣的“局部觀測算符(local operator)”)！以巨無霸西瓜的例子來說，對於內部同一個地方，在不同表面觀測及重構，可能有些會顯示是甜的，有些顯示是不甜的，甚至有些顯示會是酸的！那到底該聽誰的？要如何從這些零散的重構資訊中，得知真正的資訊？這又被稱為「AdS/Rindler謎題」。

量子糾錯

AdS/Rindler謎題告訴了物理學家在AdS/CFT對偶中，雖然有個字典能夠將表面CFT的觀測對應到內部的資訊，然而這個對應極度複雜且混亂。如果只觀測部份的表面，那麼將只能獲得部份資訊，而這些部份資訊和表面的關係是什麼呢？

之前在火牆悖論出現過的兩位熟面孔Ahmed Almheiri和Daniel Harlow，以及當時在Stanford大學的Xi Dong，三位年輕的博士後研究員在2014年底共同發表了一篇名為『Bulk locality and quantum error correction in AdS/CFT』的論文。其中標題裡的“quantum error correction(量子糾錯)”正是在第6章後半部提到量子計算機實現方法時，用來實現容錯定理的關鍵理論技術。

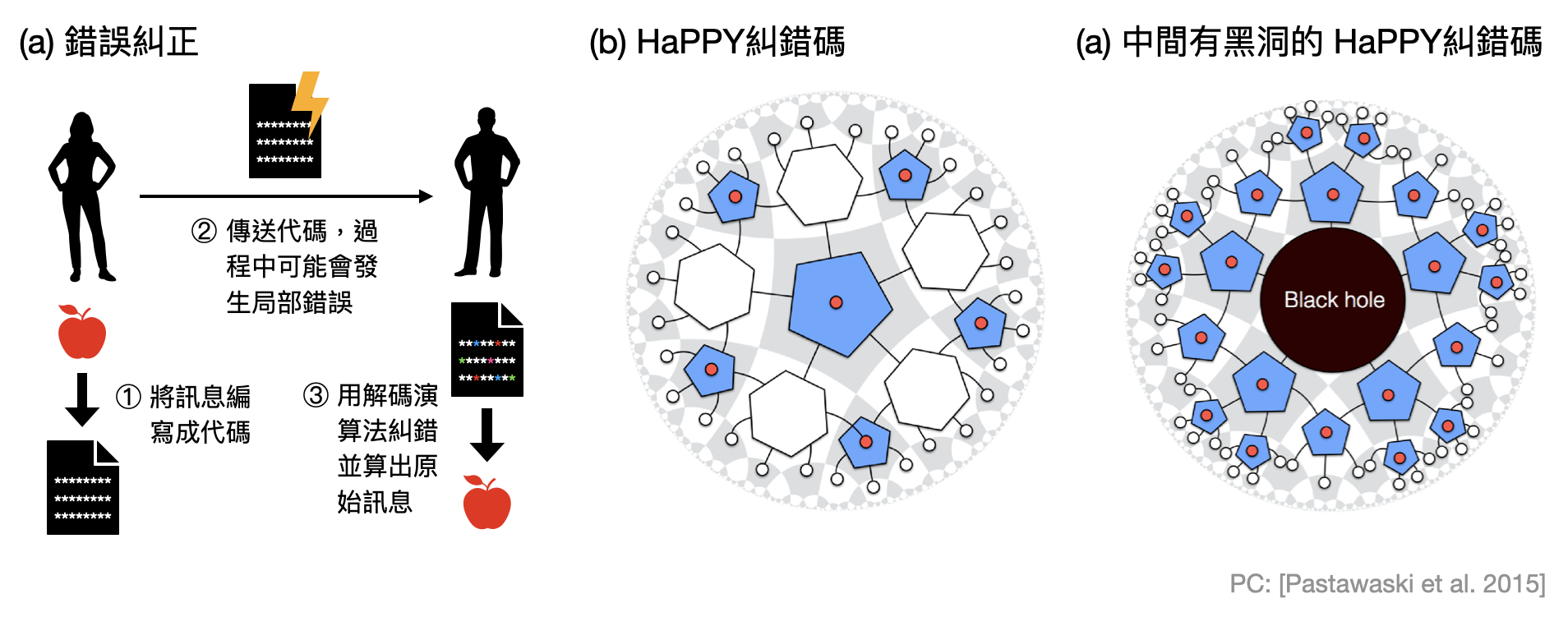
在量子糾錯(以及傳統的訊息錯誤糾正)中，訊息的傳遞者會用一個編碼演算法，將原始的資訊(例如一個量子態)加入一些冗余資訊，轉換成為一個“代碼(codeword)”，並將代碼傳算給接收者。在傳送的過程中也許會有些外在因素導致傳遞的訊息在局部發生一些錯誤。如果傳遞的是原本的資訊，那麼這些錯誤將會讓接收者無法得知原始訊息。然而如果傳遞的是糾錯代碼，那麼接收者就可以透過糾錯系統的解碼演算法成功算出原始訊息為何。

Almheiri、Dong和Harlow三人提議將AdS到CFT的過程想成是一個量子糾錯碼：AdS的內部量子態為想要傳送的訊息，CFT的表面則是其對應的糾錯代碼。如果只觀測部份的CFT表面，相當於糾錯代碼中在這個表面以外的部份都遺失了。因此，在巨無霸量子西瓜外的觀測者，需要測量足夠多的表面，然後就可以透過相對應量子糾錯碼的解碼演算法重構AdS內部某個點的資訊。

(a)錯誤糾正包含了兩個演算法：編碼演算法與解碼演算法。傳送者用編碼演算法將訊息轉為代碼，並傳給接收者。接收者則用解碼演算法揪出潛在的錯誤，並獲得原始訊息。(b)圖中為[Pastawaski et al. 2015]提出的HaPPY糾錯碼，圖中的紅色點點代表AdS空間中的位置，最外圈的白色點點則是CFT的量子態。從量子糾錯的角度可以將所有的紅色點想成是要傳送的訊息，將白色點點想成是糾錯代碼。表面重構則是將CFT解碼回AdS的過程。(c)也可以將一個黑洞放入HaPPY糾錯碼並研究其性質。例如，再加入黑洞之後，黑洞事件視界上將會多出許多新的紅點點。根據AdS的雙曲空間性質，越大的黑洞將會引入越多的紅點點。

透過量子糾錯的視角，AdS/Rindler謎題中看似雜亂無章的局部重構資訊，得以被一套乾淨的演算法描述。像這樣由計算帶來的操作型數學語言，是否能在AdS/CFT對偶未完待續的字典中做出更多貢獻？

總結

自從愛因斯坦帶領我們進入重力理論的新世紀之後，在實驗技術還沒跟上之前，理論物理學家們只能靠著數學美感和物理直覺，在一片漆黑中摸索前往量子重力的道路。霍金輻射引發對信息量的重新省思，以及雙曲與共形性質在AdS/CFT對偶間的共舞，雖然尚未帶來物理學家心中的聖杯理論，但是往回看，多年來的努力仍然激盪出許多全所未見的新理解。同時，計算的視角和語言，也悄悄地在這個理論物理的最高殿堂中參上了一腳。接下來量子重力會往哪裡走？能否從計算的角度獲得更多新觀點？讓我們繼續看下去。

延伸閱讀

教科書與其他教材：

內文提及的論文：

科普書籍：