第6章
微觀新世界:量子物理
Nobody understands quantum mechanics.
沒有人懂量子力學。
Richard Feynman
當物理學家進入了原子的尺度,古典力學開始無法解釋他們眼前看到的景象。這些“量子現象”不但催生了量子物理(quantum physics)這幢摩天大廈,其湧現的精妙數學結構更是豐富了近代理論電腦科學的發展。不過,雖然身為二十世紀以降物理學的瑰寶,量子物理仍然有著許多謎團。隨著科學的普及,越來越多冠上“量子”頭銜的語彙浮現在日常生活中,到底“量子”是什麼呢?跟計算又有什麼關係呢?
量子物理
在二十世紀初,物理學家們開始在微觀實驗中發現許多古典力學無法解釋的現象,從物理量的離散性到光的波粒二重性等等,這些“量子現象”督促著理論學家建構一個全新的物理架構來理解微觀世界。於是,在無數頂尖頭腦(例如愛因斯坦、海森堡、波爾)的激盪之下,最終眾人合力建立了全新的數學理論。這些理論不但解釋了各種五花八門的量子現象,還預測了許多新穎的物理,甚至進一步引領出創新的數學和計算理論!不過,量子理論在本質上與古典力學很不一樣的世界觀,仍然困擾著物理學家和哲學家到底該如何詮釋這些數學架構與現實世界的關聯。在本章中,我們將著重在介紹幾個經典的量子現象、基本的量子理論、以及量子物理與計算之間的糾葛。
量子現象與波粒二重性
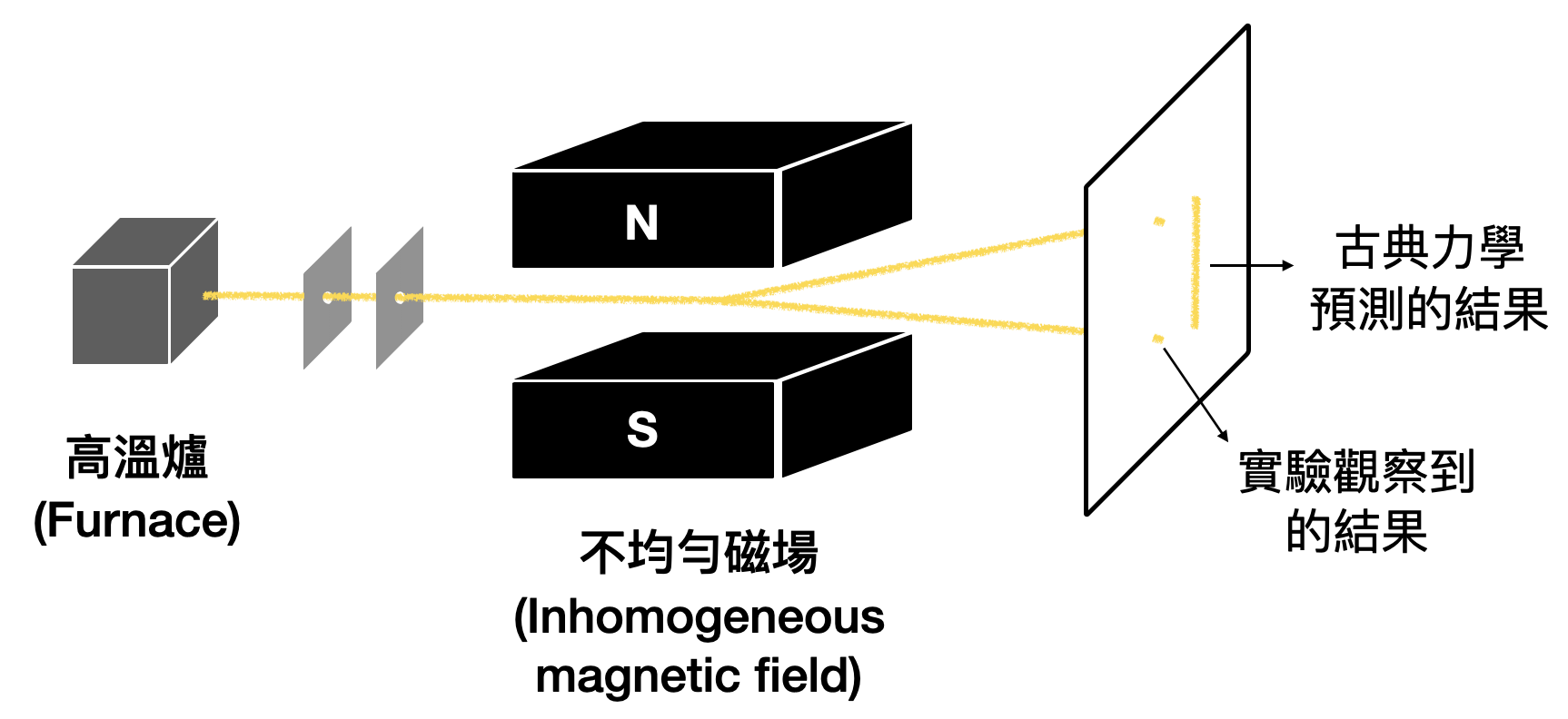
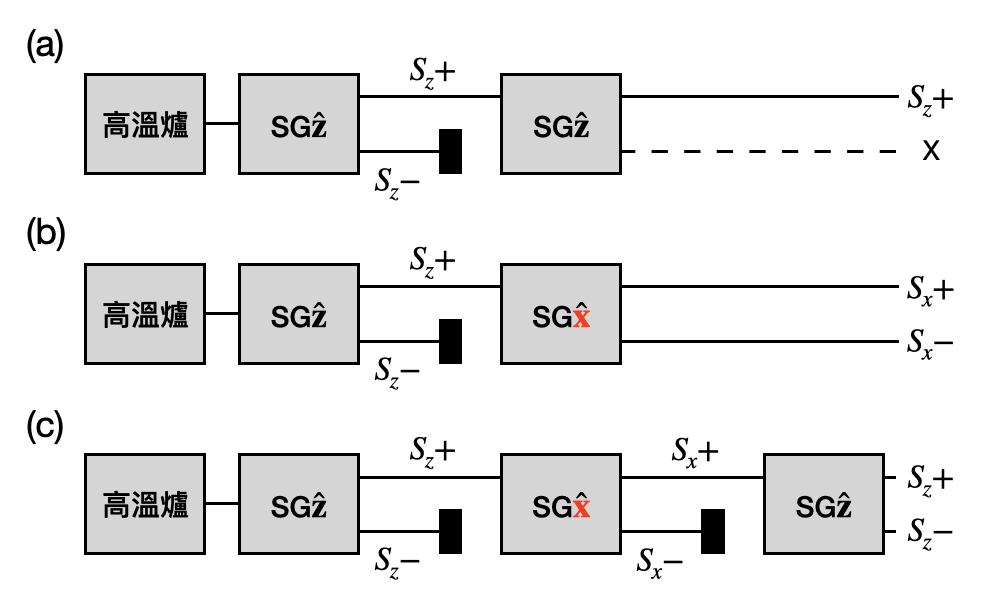
量子現象: 在古典力學的架構中,我們將許多物理量用“連續(continuous)”的變量來描述。例如,一個球的速度$v$可以是10公尺/秒,也可以是0.1公尺/秒,或是0.0001公尺/秒,也就是$v$的大小可以是任意接近於0的數字。然而,隨著實驗技術的提升,物理學家漸漸發現許多物理量竟然無法擁有任意的數值!如此只能擁有非連續數值的物理量,又被稱為「量子化(quantized)」的物理量。例如在著名的斯特恩-革拉赫實驗(Stern–Gerlach experiment)中,展示了角動量是量子化的。在下圖的詳細解說中,並不需要具有太多相關的物理知識就可以感受和理解。
波粒二重性: 提到了波和粒子,我們腦中的圖像可能是一條抖動的線和一顆小球。在物理中,波和粒子被更廣義化和抽象化為物理性質的基礎特性。「波(wave)」刻畫了具有震盪且可以相互疊加的物理性質,例如兩個不同頻率的聲波碰在一起時,可以疊加成為一個具有新的頻率的聲波。「粒子(particle)」則是對應到具有確切數值的物理性質,例如物體的質量。在古典物理的世界中,一個物理性質要嘛可以用波來描述,要嘛可以用粒子來描述。然而,在一些實驗中,物理學家漸漸發現許多物理性質竟然同時具有波和粒子的特性!這又被稱為波粒二重性(wave–particle duality)。當我們將前面提到的斯特恩-革拉赫實驗設置稍加延伸之後,就可以展示角動量具有波粒二重性!
量子物理速成班:建構量子的數學世界觀
著名的物理學家費曼(Richard Feynman, 1918-1988)曾說過:「沒有人懂量子力學(nobody understands quantum mechanics)」。在進入對量子力學比較具體的數學架構之前,必須先強調一下,量子物理中許多基本設定很難從第一原理的物理直覺去理解和解釋。在很多時候,先接受定義再透過例子慢慢感受和理解量子物理的深邃會是個更有效率的學習方式。以下我會稍微補充一些具體的數學形式,略去不看並不會影響理解,所以讀者可以根據自身的學習背景決定如何品嚐。
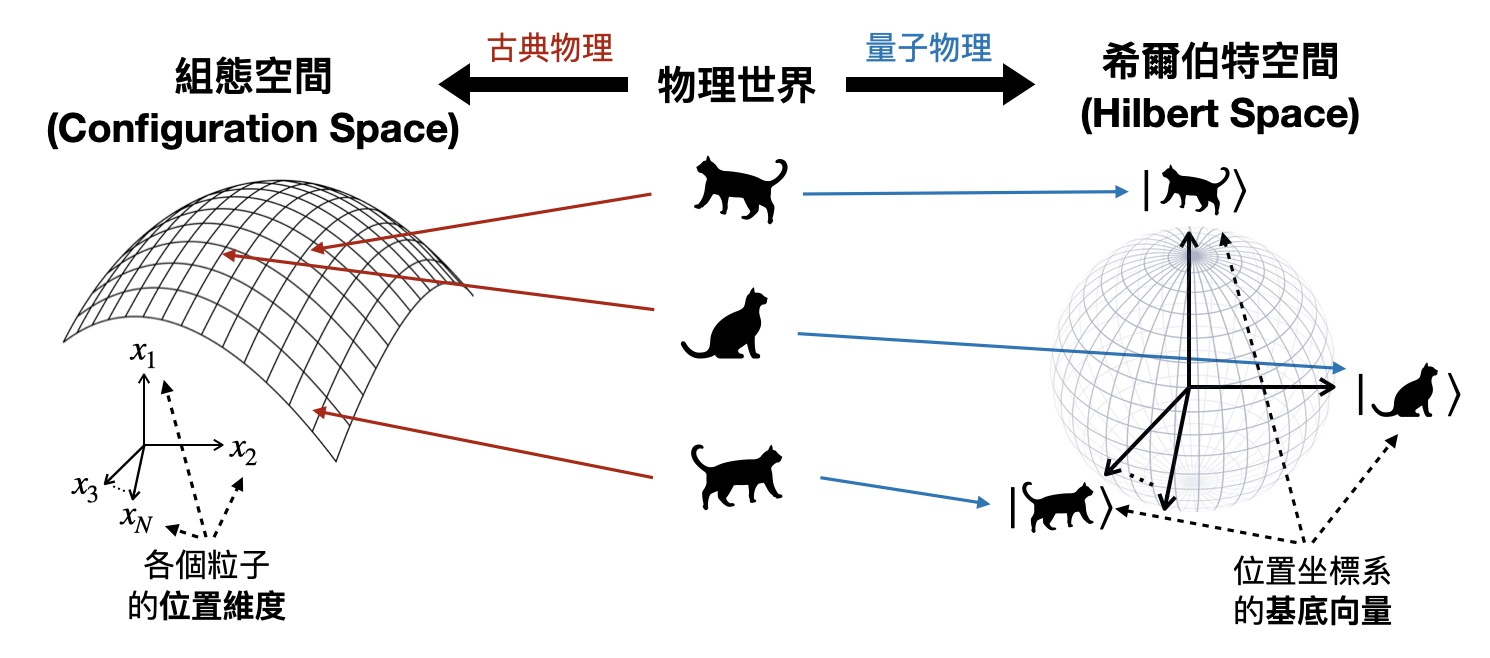
在上一章中,我們學到了牛頓力學使用三維歐式空間,而古典力學則進一步將每個粒子的座標和動量分開討論而考慮了高維度的組態空間(或是相空間)。在量子物理中,我們將移動到一個無限維度的希爾伯特空間(Hilbert space)。
為什麼要考慮無限維度的空間呢?什麼是希爾伯特空間?每個維度又代表了什麼?
在古典力學中,一個核心的假設就是物體的位置和速度是「獨立(independent)」的兩個參數。在數學上,“獨立”指的是位置和速度(和動量)在組態空間(以及相空間)中是「線性獨立的(linearly independent)」。如果讀者尚未接觸過或是不熟悉線性代數,“獨立”在這邊的物理意義是指位置和速度(和動量)是「可交換的(commutative)」。也就是說,在計算拉格朗日值、漢米爾頓值等等的時候,當需要知道物體的位置(因為需要計算位能)和速度(因為需要計算動能)時,無論先測量位置或是先測量速度都不會影響最終的結果。然而,在量子物理中,由於位置和速度(和動量)是「不可交換的(non-commutative)」觀測量,於是在數學上我們無法假設它們是獨立的,進而需要一個新的架構來描述這些量子現象。
希爾伯特空間簡單來說可以想成是歐式空間的延伸,是個能夠定義“坐標系”的無限維度空間。每個觀測量(例如位置或是動量),都會對應到一個相對應的坐標系。
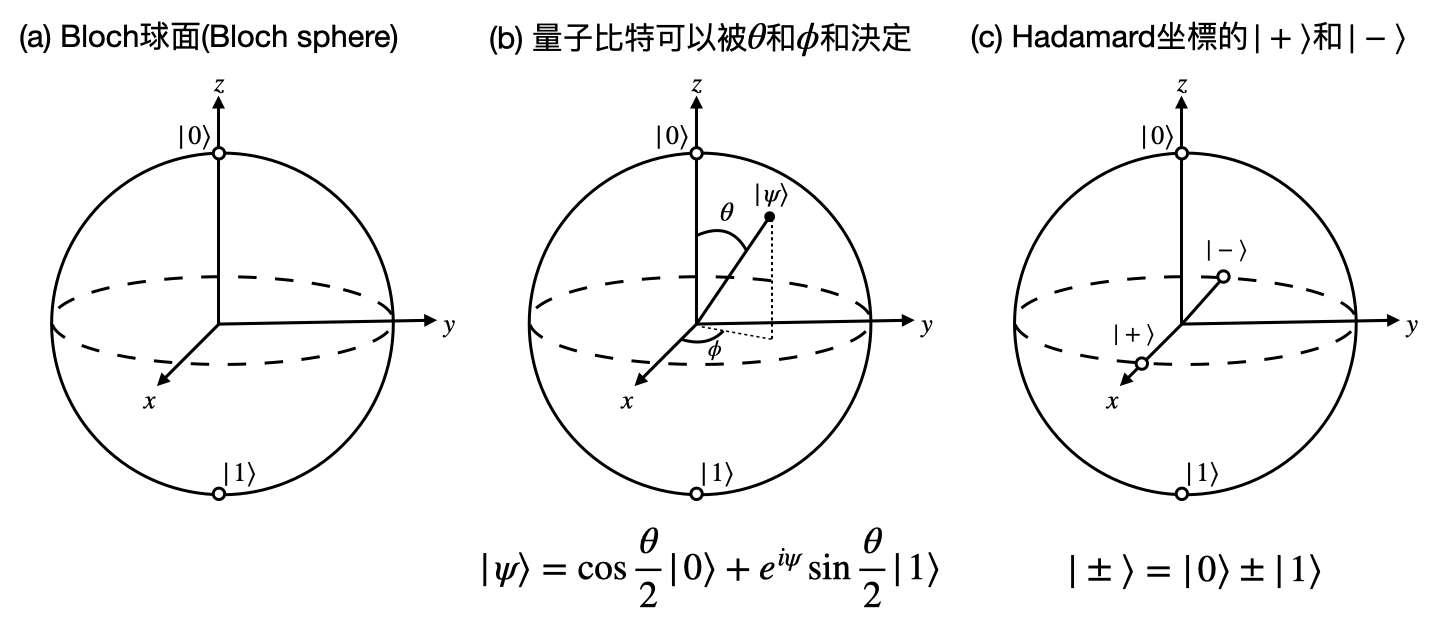
量子態(Quantum state)與bra-ket符號: 希爾伯特空間中的一個單位長向量(也就是離原點距離為1的一個點),被稱為一個量子態,將會對應到系統的一個狀態。符號上一般會使用所謂的bra-ket符號(“bra”對應到$\bra{\ }$,“ket”對應到$\ket{\ }$),例如一個系統的量子態在一般情況下我們會標記為$\ket{\psi}$。
可測量、算符和特徵態: 可測量(observable)指的是在我們關注的系統中,可以透過實驗獲得的資訊。在量子系統中,一個可測量將會對應到希爾伯特空間中的一個算符(operator),兩個常見的算符分別為位置算符(position operator)和動量算符(momentum operator),在接下來的討論中,讓我們用位置算符$\hat{X}$作為例子(並且考慮一個粒子在一維空間中的位置)。
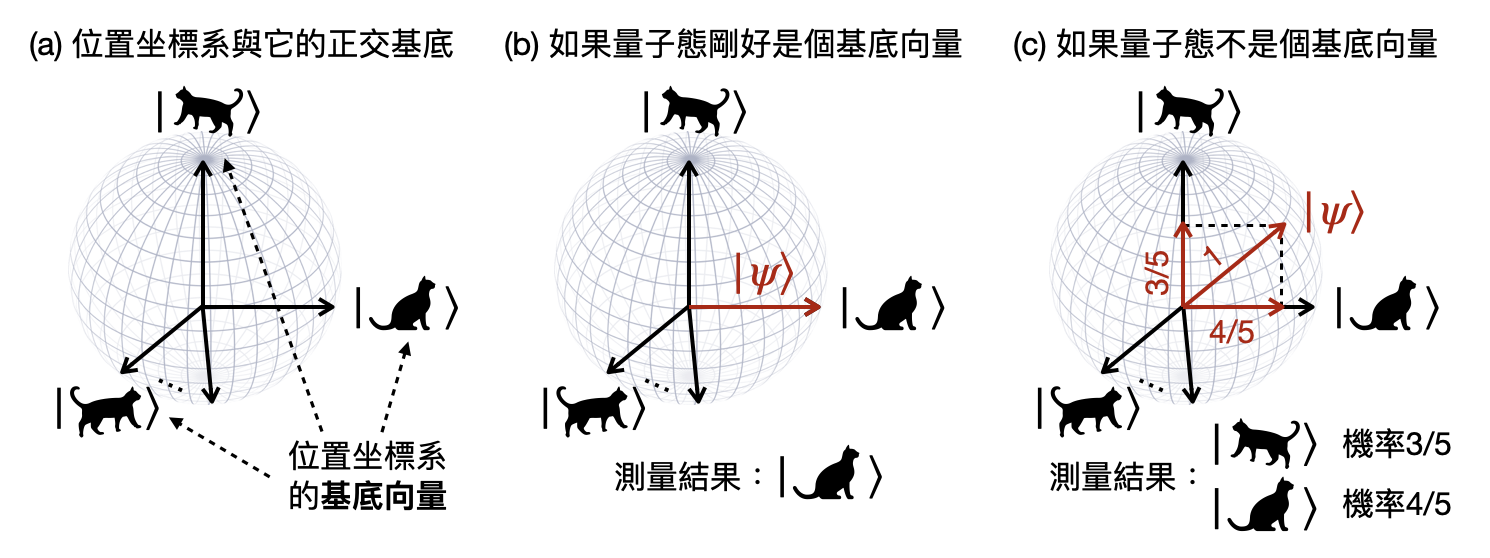
一個量子系統的可測量,對應到的是一組(無限多個)特徵態,每個特徵態對應到一個可能的測量結果。在數學上,這些特徵態將會組成希爾伯特空間的一組正交基底(orthonormal basis),幾何圖像上就是希爾伯特空間的一個坐標系,每個基底向量(在這邊就是一個特徵態)都是互相垂直的。
當測量位置時,我們會獲得的是一個數值$x$,告訴我們粒子現在的位置坐標是多少。而位置算符$\hat{X}$的功用,就是在數學操作上實現這件事情!具體來說,如果量子態$\ket{\psi}$是對應到一個正在位置$x$的粒子,那麼我們將會有以下這個式子。 \begin{equation*} \hat{X}\ket{\psi}=x\ket{x} \, . \end{equation*} 左式$\hat{X}\ket{\psi}$代表將算符$\hat{X}$作用在量子態$\ket{\psi}$上面,右式$x\ket{x}$則代表獲得的觀測結果為$x$,然後量子態變成$\ket{x}$。其中$\ket{x}$是位置算符的一個特徵態(eigenstate),代表說使用算符$\hat{X}$作用在它上面並不會改變這個量子態。在上面的例子中,其實原本的量子態$\ket{\psi}$就是這個特徵態$\ket{x}$。
波恩規則(Born rule): 如前面提到的,一個觀測量會對應到一個測量坐標系,而測量這個動作,則會對應到把量子態(也就是希爾伯特空間中的一個單位長向量)投影到坐標系的基底向量(也就是其中一個特徵態)上面。如果量子態剛好就是其中一個特徵態,那麼測量的結果就直接會是這個特徵態對應到的特徵值(例如下圖(b))。但如果量子態$\ket{\psi}$不是其中一個特徵態,那麼我們將會根據$\ket{\psi}$和各個特徵態$\ket{x}$之間的重合長度$\braket{x}{\psi}$,依照比例按機率來決定要投影到哪一個基底向量(例如下圖(c))。這種投影的方式,又被稱為波恩規則(Born rule)。
純態(Pure state)與混合態(Mixed state): 目前為止我們討論到的量子態,無論是否為某個測量坐標系的基底向量,都是一個純態。一旦測量了一個並不是基底向量的純態,根據波恩規則,測量的結果將可能是數個基底量子態的其中之一(例如上圖(c))。也就是說,測量的結果是許多純態的機率分佈。這樣一個參雜“(古典)機率”的測量結果,又被稱為混合態。
重新審視量子現象:測不準原理與互補原理
講了這麼多次“位置和動量是不可交換的觀測量”,在數學上這被不可交換的矩陣算符描述,而在物理實際中則是對應到觀測準確度的極限。具體來說,Werner Heisenberg(1901-1976)精準地用「測不準原理(uncertainty principle)」告訴了物理學家同時觀測任意兩個可測量時,兩個數值測量準確度的下界:
測不準原理:$\sigma_A\sigma_B\geq\frac{1}{2}|\langle[\hat{A},\hat{B}]\rangle|$。其中$\sigma_O$是相對應算符$\hat{O}$測量時的標準差,另外$[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}$是(i)先觀測B在觀測A和(ii)先觀測A在觀測B,這兩種測量順序得出的結果之間的差距。最後,$\langle\hat{O}\rangle$則是測量$O$的期望值。
乍看之下,測不準原理是個數學定理。雖然的確符合實際在微觀尺度發生的現象,但是該怎麼從物理的角度理解呢?
著名的丹麥物理學家Niels Bohr(1885-1962)曾經是Heisenberg的老師,在讀了Heisenberg關於測不準原理的草稿後,Bohr指出他在對量子力學所提倡的哥本哈根詮釋中,就已經用「互補原理(principle of complementarity)」替測不準原理提供了一個帶有哲學風味的物理解讀。
就像之前在量子現象章節時提到的波粒二重性,我們既能夠觀察到光作為波所蘊含的性質,也能測量到其身為粒子時具有的特性。但是,我們沒辦法同時見證這兩個觀點,只能透過重複在這兩種觀點反覆地實驗,讓它們各自的結果互補對方視角的缺失。如此兩種視角互補的現象,Bohr認為是物理世界中的原則,而且並不是只有在光的波粒二重性中出現,位置和動量的測量,以及測不準原理中一對相互不可交換的算符,都是互補原理下的相互輝映的影子。
The opposite of a fact is falsehood, but the opposite of one profound truth may very well be another profound truth.
一個事實的反面是謬誤,但是一個深刻真理的反面也很有可能是另一個深刻的真理。
Niels Bohr
量子世界的演化規則:薛丁格方程式
現在我們知道在量子力學中,一個物體(或是一個系統)的狀態對應到了希爾伯特空間中的一個單位向量,於是探討物體的變化將會等價於研究這個向量是如何演化的。如同在牛頓力學,三大定律告訴我們該如何計算系統下一個時間點的狀態,在量子力學中,著名的薛丁格方程式(Schrödinger equation)則告訴我們一個量子系統是如何演化。
薛丁格方程式:$i\hbar\frac{\partial}{\partial t}\ket{\psi} = \hat{H}\ket{\psi}$。
第一次看到薛丁格方程式的讀者先別害怕,以下我們將先從高觀點的視角了解其背後的操作型定義。感興趣的讀者歡迎從本小節末的延伸內容理解每個符號的意思以及整個方程式背後的直覺意義。
在薛丁格方程式$i\hbar\frac{\partial}{\partial t}\ket{\psi} = \hat{H}\ket{\psi}$中,方程的左式是關於量子態演變的方向(並且被兩個常數稍微做單位的調整),而方程的右式則是關於量子態當下的能量。也就是說,薛丁格方程式本質上是告訴我們,量子態演化的方向,是根據當下的能量來決定的。
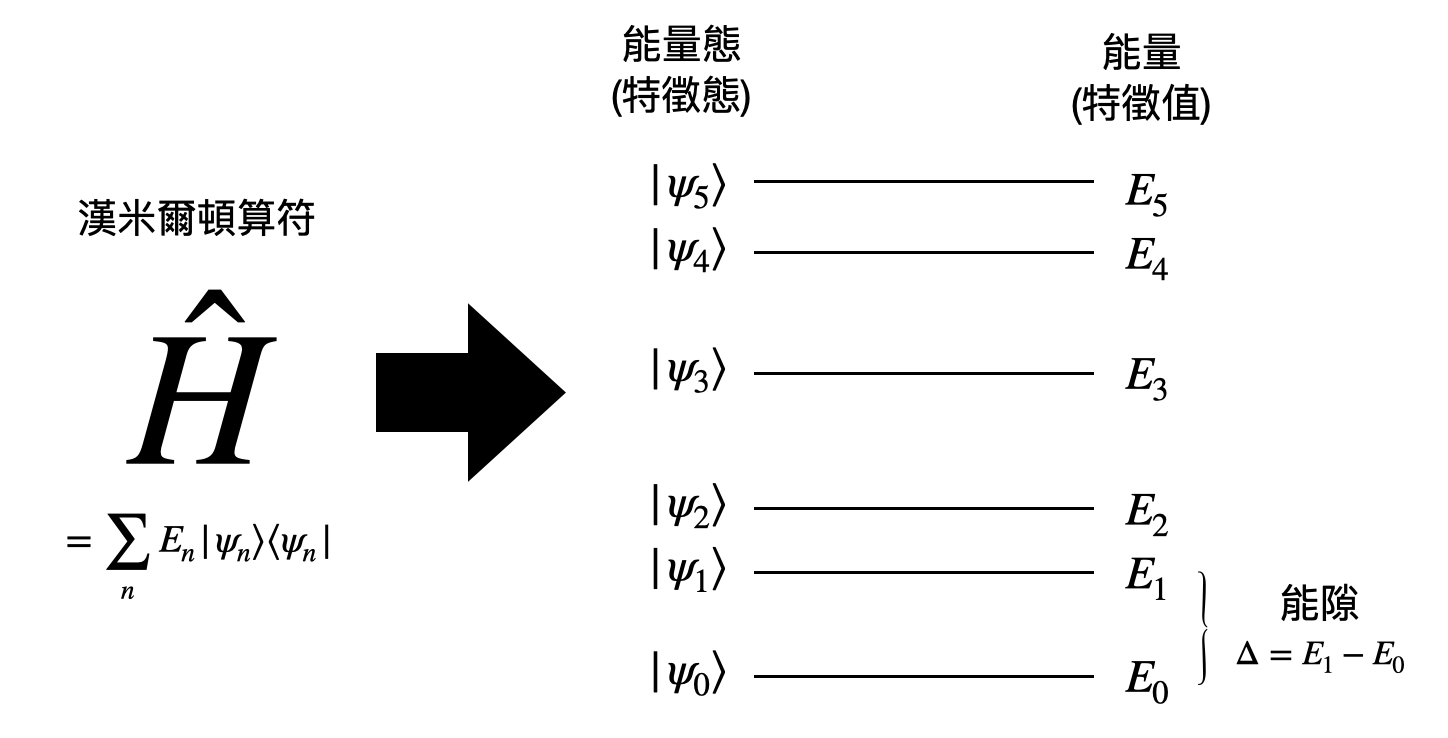
而系統的能量是被所謂的漢米爾頓算符(Hamiltonian operator)$\hat{H}$刻畫。漢米爾頓算符中記錄了所有可能的“標準狀態”,或是術語上又被稱為特徵態。直觀上來說,如果說漢米爾頓算符刻畫了社會的運行方式,那這些標準狀態就像是社會中的各種職業,例如棒球員、音樂家、老師、法官等等,對於非常專一的人(量子態)來說,漢米爾頓算符會指引他們走一個非常特定的路徑,讓他們一直在自己想走的道路上(也就是個特徵態)。而對一般人來說,也許對好幾個不同的職業都感興趣,於是成為了這些職業的一個疊加態,並在漢米爾頓算符的指引下載浮載沉。
量子力學的世界觀:(1)定義一個系統的漢米爾頓算符,(2)解相對應的薛丁格方程式。
首先,$i$是虛數(imaginary number),是$-1$的平方根,也就是說$i^2=-1$。虛數在數學中有著極重要的地位,然而受限於篇幅和主題,在此我們無法深入探究其精妙之處。不過在這邊可以簡單提一個關於虛數重要的特性:在薛丁格方程式中,虛數$i$保證了量子態$\ket{\psi}$在演化的過程中可以一直維持相同的長度,以數學的專業術語來說,虛數$i$(以及$\hat{H}$的性質)讓量子態的演化是么正的(unitary)。
再來,$\hbar$是約化普朗克常數(reduced Plank constant),其數值大約是$1.055\times10^{34}J\cdot s$。約化普朗克常數和普朗克常數($h=2\pi\hbar$)是量子物理中的重要常數之一,它們刻畫了量子世界中的尺度大小。對於首次接觸量子物理的讀者來說,可以先將$\hbar$和$h$想成是非常小的一個數字,會在各種量子物理的基礎方程式中扮演著調整尺度的角色。
接著,$\frac{\partial}{\partial t}$指的是對量子態$\ket{\psi}$對時間做偏微分。直覺上的意義是在探討$\ket{\psi}$在某個瞬間會往哪個方向移動,類似於平常我們所說的“速度”。於是,薛丁格方程式在數學上其實就是個一階偏微分方程式。如此與本質上為二階偏微分方程的古典力學的差異處,使量子力學的演化具有線性疊加的性質:兩個符合薛丁格方程式的波函數相加後,仍然會符合薛丁格方程式。這個特殊的性質,我們將會在後面的段落好好探討。
最後,$\hat{H}$是所謂的漢米爾頓算符。在之前關於古典力學的章節中,我們提到漢米爾頓量$H$刻畫了一個系統的能量。而在量子物理中,$\hat{H}\ket{\psi}$代表了從系統$\ket{\psi}$中提取出能量。稍微深入一點來說,漢
米爾頓算符是個厄米性(Hermitian)的算符(有時候又被稱為是自伴性(self-adjoint)的),於是會保證其特徵值(eigenvalue)都是實數的。而漢米爾頓算符的特徵值可以被解讀為相對應特徵向量(eigenvector)的能量。於是,$\hat{H}\ket{\psi}$可以被理解為,先將量子態$\ket{\psi}$根據漢米爾頓算符$\hat{H}$的特徵基底(eigenbasis)做分解,在根據相對應的能量做拉伸。
如果漢米爾頓算符$\hat{H}$不會隨著時間改變(time independent),而且初始態可以被能量態(參考上圖)展開為$\ket{\phi}=\sum_jc_j\ket{\psi_j}$,那麼$\ket{\phi}$經過時間$t$的演化後,將可以被寫成 \begin{equation*} e^{i\hat{H}t/\hbar}\ket{\phi_0} = \sum_j e^{-iE_jt/\hbar}\ket{\psi_j} \, . \end{equation*}
從數學架構中發現的新性質:量子疊加與量子糾纏
一提到“量子”,五花八門的行業諸如量子波動速讀、量子占卜、量子農業等等,在坊間打著量子物理的旗幟招搖撞騙。這些“偽科技”不外乎使用一些量子力學中的基本概念,移花接木套用到毫不相關且無科學根據的事情上。而最常被使用的概念大概就是「量子疊加(quantum superposition)」和「量子糾纏(quantum entanglement)」了!在更進一步理解量子物理和計算之間的關聯前,我們必須先建立對這兩個概念的基本認識,同時也希望能讓讀者在未來遇到量子騙術時,能夠識破其中的誤曲!
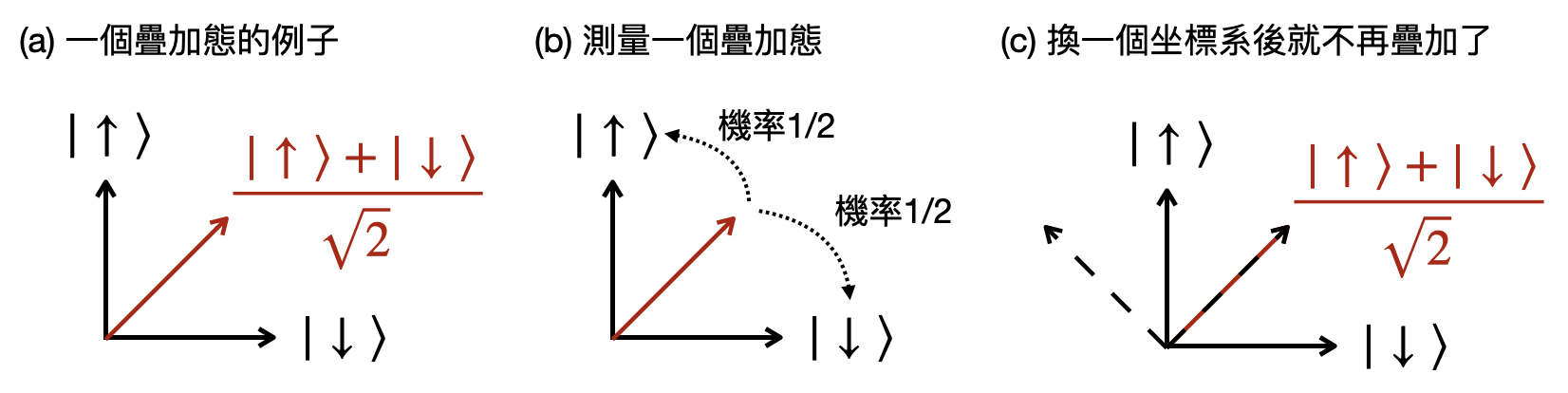
量子疊加: 一個對疊加態常見的小誤解是:把量子疊加想成就是結果有超過一種的可能性。這樣的理解可以算是半對半錯。對的地方在於,一個疊加態在某些測量坐標系之下,的確會有超過一種可能的測量結果。錯的地方則在於,一旦換了測量坐標系,將可能只會有一種可能的測量結果。除此之外,當擲了一個硬幣後,在缺少足夠資訊的情況之下,硬幣的結果既可能是正面的也可能是反面的,但這不代表此時硬幣是處在一個疊加態!也就是說,“有超過一種的可能性”只是量子疊加的一個性質而非它的定義!
那疊加態到底是什麼呢?和機率的關係又是什麼?
首先,掌控量子力學中動力演化的薛丁格方程式是「線性的(linear)」。也就是說,考慮兩個量子態的演化$\ket{\psi(t)}$和$\ket{\phi(t)}$,它們兩個的線性疊加(也就是$\ket{\psi(t)}+\ket{\phi(t)}$然後除上一個常數確保結果是單位長的)也將會是個合法的量子態演化過程!注意到這樣的疊加性質是在古典力學中所沒有的!
那我們該如何理解這樣的疊加性質呢?在量子物理的基本設定中,我們學到了物體的一個狀態在希爾伯特空間被表示為一個單位向量,而測量這個狀態的某個物理性質則是對應到選取一個坐標系並將量子態根據波恩規則投影上去。當一個量子態是多個特徵態的疊加時(也就是沒有和其中一個座標軸平行),將會有超過一種可能的測量結果。
總結來說,疊加態本身是一個量子態,並沒有任何機率牽扯其中。只有當測量之後,其測量結果才會有隨機性產生。另外,一旦換了一個測量坐標系,疊加態就很有可能不再是疊加的了(例如下圖的例子)!
量子糾纏:在量子物理早期的研究階段,有個著名的EPR悖論(Einstein–Podolsky–Rosen paradox),困擾了包括愛因斯坦在內無數的物理學家。而其中的關鍵就是所謂的量子糾纏。在具體的解釋量子糾纏為何之前,先來看看EPR悖論是什麼吧!
讓我們先從建立一些基礎的概念開始。在電子(electron)中,有個重要的性質叫做自旋(spin),一個電子的自旋值可以是“朝上$\uparrow$”或是“朝下$\downarrow$”。所以我們可以使用$\ket{\uparrow}$和$\ket{\downarrow}$來分別表示一個自旋朝上和自旋朝下的電子狀態。現在讓我們考慮具有兩個電子的系統,根據四種可能的自旋組合,系統可能處於以下四種量子態或是它們的疊加:$\ket{\uparrow\uparrow},\ket{\uparrow\downarrow},\ket{\downarrow\uparrow},\ket{\downarrow\downarrow}$,其中的兩個箭頭分別表示了兩個電子各自的自旋方向。
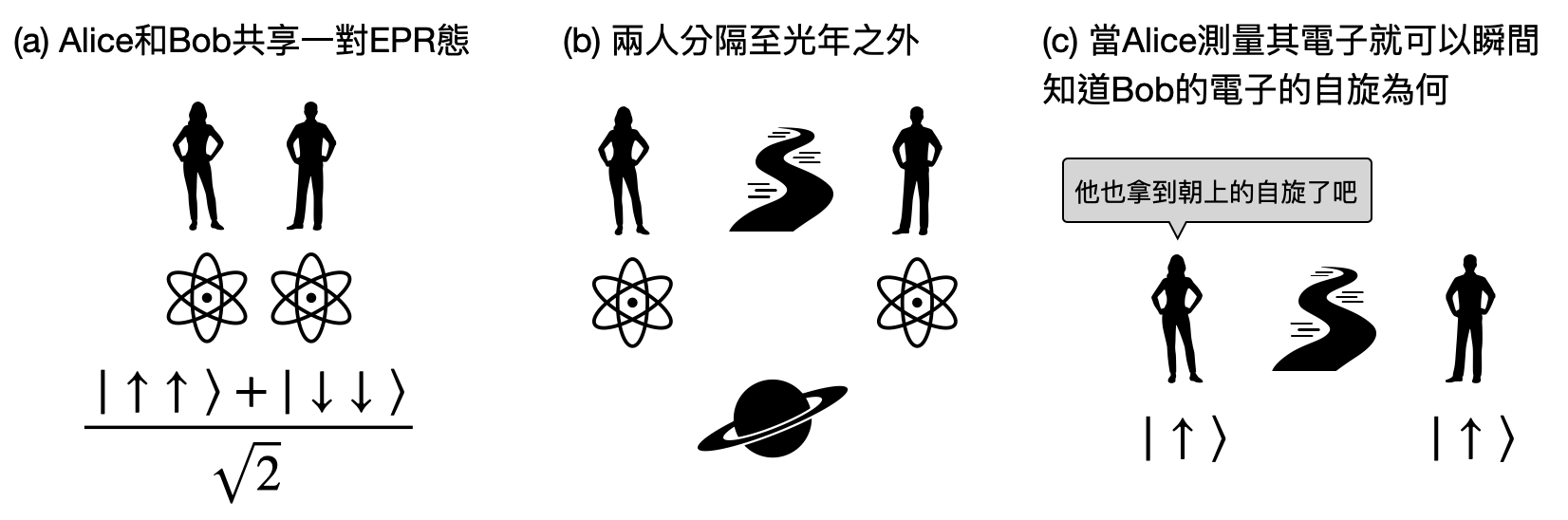
EPR悖論考慮了以下這個有趣的思想實驗:首先,準備具有疊加態$(\ket{\uparrow\uparrow}+\ket{\downarrow\downarrow})/\sqrt{2}$的兩個電子。為了紀念三位發現量子糾纏的科學家,這個特殊的量子態又被稱為「EPR對子(EPR pairs)」。接著,將兩個電子之間的距離拉得非常非常遠,然後測量其中一個的自旋方向。根據波恩規則,我們知道測量的結果有50%的機率是得到朝上的自旋$\uparrow$,以及有50%的機率得到朝下的自旋$\downarrow$,更特別的是,根據這個疊加態的取法,我們知道兩個電子的自旋方向會是相同的!當年愛因斯坦等人發現這個情況時,曾經因此覺得量子力學的設定是錯誤的:如果可以藉由得知其中一個電子的自旋方向而“立刻”知道另一個電子的自旋方向,那豈不是可以超越光速的傳遞訊息了!?
不過在物理學家們多年的討論之下,現在我們已經對EPR悖論有了更深入的理解。簡單來說,雖然在測量了其中一個電子的自旋方向後,我們就可以立刻知道另一個電子的自旋方向,然而由於我們無法掌控自旋測量的結果(根據波恩規則),所以我們其實並不能透過這個疊加態來傳遞訊息!
如果再更進一步探討下去,EPR悖論中的這個特殊疊加態$(\ket{\uparrow\uparrow}+\ket{\downarrow\downarrow})/\sqrt{2}$,是個無法被表示成兩個“獨立”的量子態的合併(專業術語上稱為直積態(product state))。而這種類型的量子態又被稱為具有量子糾纏。這是只有在量子物理中才會有的狀態,許多有趣的量子現象也都是和量子糾纏息息相關。
量子糾纏的威力:Bell定理和CHSH遊戲
目前為止,我們看到了量子力學在量子疊加和量子糾纏上面有著和古典力學很不一樣的現象。不過除了這些表象的差異之外,有沒有什麼事情只有在量子的世界做得到而在古典的世界做不到呢?
John Bell(1928-1990)是個粒子物理學家,長年在著名的歐洲核子研究組織(CERN)工作。1963他休假來到了史丹佛大學,並在隔年回CERN返工之後,發了一篇和他平常研究不太一樣的論文『On the Einstein–Podolsky–Rosen paradox』。沒錯,論文標題中就是之前提到的EPR悖論!在這篇不尋常的工作中,Bell拓展了EPR悖論的想法,提出了一個實驗想法,可以用來挑戰量子力學是否可以被古典理論解釋。
具體來說,論文中提出的Bell定理,或稱Bell不等式(Bell’s inequality),用數學證明了古典理論(以及更廣義一點的局部隱變數理論)在Bell實驗中的最佳表現有個上界,同時在理論上可以透過使用EPR態超出這個上界。不到二十年的時間,數位實驗學家相繼展示如何用量子實驗突破Bell不等式的上界,成功告訴了全世界,量子世界無法被古典的理論解釋。其中Alain Aspect、John Clauser和Anton Zeilinger在2022年獲得了諾貝爾物理學獎。
那現在讓我們來看看Bell定理到底在說些什麼吧!以下我們將使用一個簡化的版本,又稱為CHSH遊戲(CHSH game)。
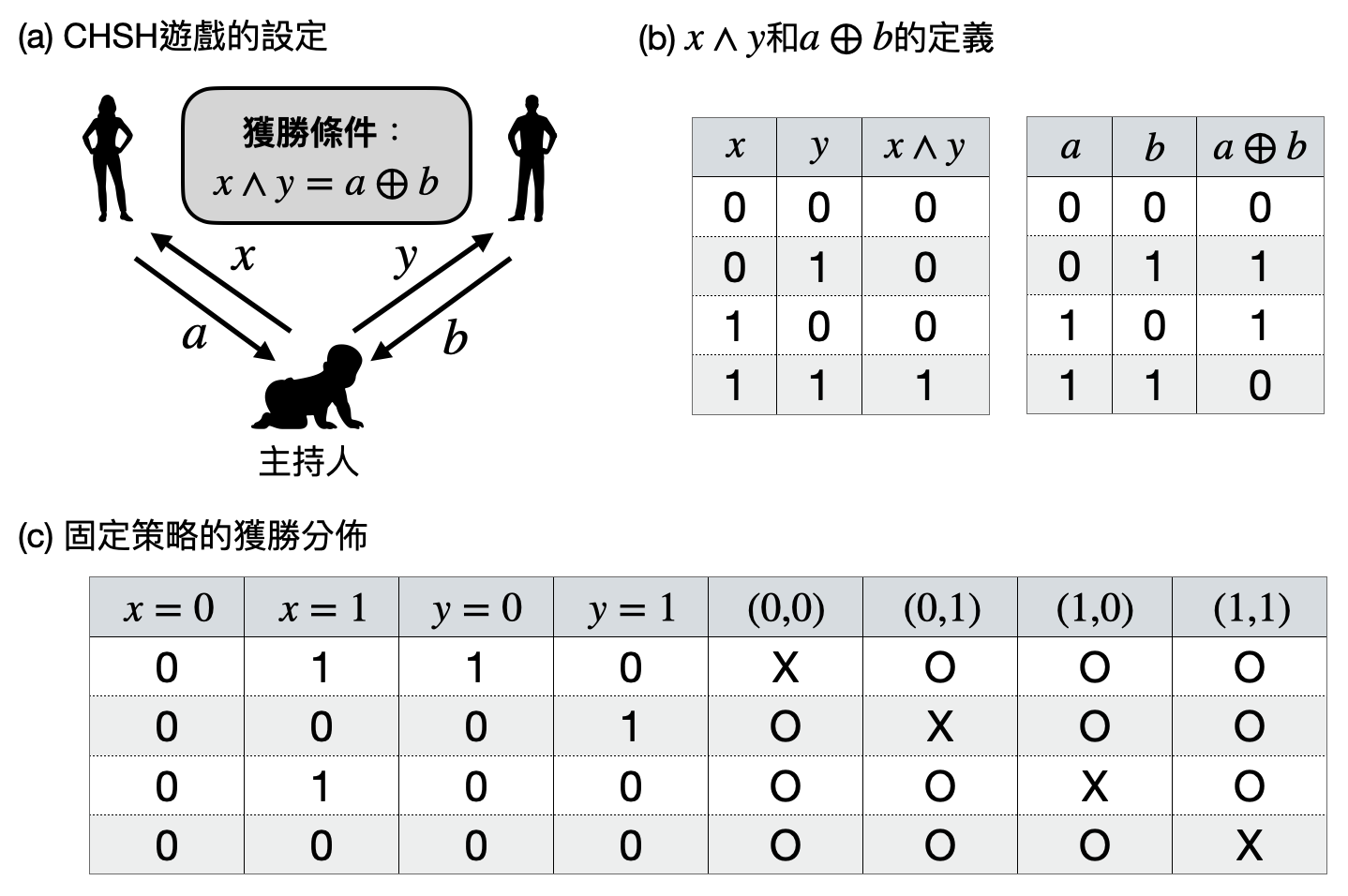
想像你和一位朋友去參加一個考驗默契的遊戲。首先,主持人準備了一個雙色的硬幣,一面是黑色、一面是白色,而且原本是黑色那面朝上擺著。接著,主持人分別給你們黑色或白色的顏料,然後要求你們在無法討論的情況之下回覆決定各自是否想要把那個硬幣翻面。如果最後硬幣根據你們的決定翻面完後的顏色,和分送給你們的顏料混合後的顏色相同,那你們就贏了。
讓我們進一步用符號來簡化之後的討論:用$x$和$y$來表示你們各自收到顏料的顏色(其中取值為1時代表白色,取值為0來時代表黑色)。另外用$a$和$b$來表示你們各自是否想把硬幣翻面(取值為1是翻面,取值為0則是不翻面)。那麼獲勝的條件等價於$x\wedge y=a\oplus b$,其中$x\wedge y$指的是“$x$和$y$”也就是$x\wedge y=1$當且僅當$x=y=1$。而$a\oplus b$指的是$a+b$除2的餘數。
什麼策略可以讓你們的勝率很高呢?
如果你們使用的是一個“固定策略”,也就是你們事先溝通好看到什麼顏色的顏料($x$和$y$)後,分別要回答什麼($a$和$b$),那麼經過一些簡單的驗算之後,可以發現只少會有一種可能的$(x,y)$值會讓你們無法獲勝。例如你總是取$a=x$而你的朋友總是取$b=1-y$,那麼只有當$(x=0,y=0)$時你們才會輸掉(如下圖(c)的第二行)。於是,如果主持人均勻地隨機選取$x$和$y$的值,那麼這個策略將會帶給你們75%
的勝率。然而,一旦主持人知道你們的(固定)策略,就可以故意選取相對應的$(x,y)$讓你們總是輸掉。
那如果可以使用“隨機策略”呢?在下圖(c)中,有四個固定策略分別只會在不同的$(x,y)$值輸掉,於是如果你們均勻地從這四個固定策略中隨機選一個,那麼就算主持人知道你們要用這樣的隨機策略,你們仍然可以有75%的獲勝機率!
在對CHSH遊戲有了一些基礎的理解之後,我們終於可以來講講Bell定理倒底說了些什麼:Bell告訴我們,當玩家的策略是“古典”的時候,那麼最高的勝率將會是75%。然而,如果玩家的策略是“量
子”的時候,則可以到達大約85%的勝率!這告訴了我們,之前看到一些量子物理中神秘的現象,竟然可以被拿來玩遊戲,還玩得比古典的策略還要好!
和古典力學做比較:路徑積分表述
在進入量子計算的討論之前,最後讓我們看看薛丁格方程式之外,另一個(等價的)描述量子系統演化的方式!
對之前古典力學篇章還有印象的讀者來說,可能還記得所謂的「最小作用量原理」,講述一個物理系統會選擇作用量最小的那條路徑來演化。在量子世界有沒有相對應的原理呢?量子物理的路徑積分表述(Path integral formulation)就正是對這個問題的回應!
和古典力學很不一樣的是,在量子世界中,並不見得只有一條路徑被選中!這其實在之前薛丁格方程式還有量子疊加的討論中,就約略提示到了:由於薛丁格方程式是線性的,將可能會有許多量子態的演化路徑都是合法的。因此,最終演化的方式將會是這些路徑的疊加!當然,如果要把路徑積分表述的細節講清楚還需要再補充許多背景知識,因此在這邊讓我們直接欣賞結論,有興趣的讀者可以參考章節末推薦的延伸閱讀。
\begin{equation*} \bra{\psi}e^{i\hat{H}t}\ket{\psi_0} = \int Dq(t)e^{iS[q,\dot{q}]} \end{equation*} 其中$\int Dq(t)$會將所有起點為$\ket{\psi_0}$和終點為$\ket{\psi}$的路徑做加權平均,而每條路徑$q(t)$的權重(或更準確來說,是$q(t)$的相位)則是複數$e^{iS[q,\dot{q}]}$。$S[q,\dot{q}]$是在古典力學部分提到的作用量。
從量子物理的路徑積分表述中,我們可以更深刻的感受到量子世界和古典世界的不同:後者根據最小作用量原理,會選擇作用量最小的路徑。而前者則是會考慮所有的路徑,並根據各自的作用量,做一個加權(相位)平均!如此“平行”的演化,也正呼應了之前特別強調的量子疊加。
量子計算
從Bell定理和CHSH遊戲中,我們看到了量子物理中的特性(像是量子疊加、量子糾纏)如何做到一些古典物理世界做不到的事情。那我們是不是可以利用這些量子的特性,在計算上面做得比(古典的)圖靈機還快呢?
從1960年代開始,就有物理學家開始醞釀建構使用了量子物理的計算系統。直到了1980年代,經過數名物理學家、數學家和計算機科學家開創性的研究,終於逐漸定型出「量子圖靈機(quantum Turing machine)」和「量子線路(quantum circuit)」的理論定義。建立在這些數學模型之上,越來越多人開始設計各種「量子演算法(quantum algorithm)」,試圖理解量子的特性是否可以在某些計算問題上提供加速。在一連串精彩的研究發展之下,最終由Peter Shor在1994年提出的Shor演算法(Shor algorithm)引起了全世界對量子計算的關注:Shor發現量子電腦在理論上可以很快速的破解一大類密碼學核心的計算問題,也就是說,如果大規模的量子電腦可以被實作出來,那麼許多現實生活中使用到的金融密碼系統將不再安全!
量子計算如今常出現在日常對話中,並且容易被有心人士拿來誤導民眾。同時,學習量子計算需要具有物理、計算機科學與數學的相關知識,因此常常令人望之卻步,或是中途放棄。如果讀者已經撐過了本書目前為止的篇章,那麼其實已經具有一些背景可以試著淺嚐量子計算的風韻。在本章剩餘的篇幅中,我們將會先看到量子電腦的基礎理論設定,了解其和古典計算模型有何不同。屆時,之前學習到量子物理的特性也會馬上派上用場。接著,我們將會從兩個量子演算法中,看到量子計算和古典計算的不同,以及前者是如何達到加速。最後,我們將簡單討論量子電腦目前和實作相關的情況。
量子訊息與量子通訊
在討論計算之前,我們同樣需要先從底層的語言說起。
古典比特(classical bit)與量子比特(qubit): 在之前的章節中,我們看到在古典的計算世界中,所有計算都是建構在0與1的二進位語言之上:計算問題的輸入與輸出是用0與1組成的字串來表示的,最基礎的單位是一個比特(bit),為了和之後量子的設定做區別,有時候我們又稱之為古典比特(classical bit)。在數學上比特是一個取值為0或是1的變數,在工程上則是被一個電晶體實現,用其電位的高或低來表示1或是0。而計算的過程,就是不停地將0與1的字串,透過一連串的簡單操作修改達成。
在量子計算的世界中,最基礎的元件則是量子比特(qubit)。在數學上,和古典比特不同的是,量子比特不再是一個取值為0或是1的變數,而是個在二維希爾伯特空間的量子態。在實作層面,我們則可以想成是一個自旋可以為上或是下的電子。看到這邊,相信許多沒接觸過量子計算的讀者應該已經有點暈頭轉向了,讓我們用比較操作性的定義再來好好介紹量子比特一遍。
一個量子比特在數學上會被一個二維向量表示,例如$\alpha\ket{0}+\beta\ket{1}$,其中$\alpha$和$\beta$又被稱為這個量子比特的波長(amplitude),它們的取值都是複數(complex number),並且$|\alpha|^2+|\beta|^2=1$。也就是說一個量子比特是個單位長的二維複數值向量,其中$\ket{0}$和$\ket{1}$形成了這個量子比特所處的希爾伯特空間中的一個(正交)座標。然而,我們並不能直接讀取一個量子比特的波長(也就是$\alpha$和$\beta$),唯一獲取關於這個量子比特信息的方式只能透過「測量(measurement)」。和之前量子物理中的測量一樣的是,我們首先需要選擇一個坐標系,然後將這個量子比特投影到這個坐標系上。最終測量後獲得的結果,將會根據投影的長度決定。舉例來說,如果用$\ket{0}$和$\ket{1}$組成的坐標系來測量$\ket{0}/\sqrt{2}+\ket{1}/\sqrt{2}$,將會有50%的機率得到$\ket{0}$以及50%的機率得到$\ket{1}$。另外一個常見的測量坐標系為Hadamard坐標系,其基底態為$\ket{+}=\ket{0}/\sqrt{2}+\ket{1}/\sqrt{2}$和$\ket{-}=\ket{0}/\sqrt{2}-\ket{1}/\sqrt{2}$,對於剛才提到的量子比特$\ket{0}/\sqrt{2}+\ket{1}/\sqrt{2}$來說,用$\ket{+}$和$\ket{-}$組成的Hadamard坐標系來測量將會有100%的機率得到$\ket{+}$。
多個量子比特: 那如果有很多個量子比特呢?之前我們提到一個量子比特是個活在二維希爾伯特空間的單位長向量,而當一個系統中有$n$個量子比特時,這整個系統則是個活在一個$2^n$維的希爾伯特空間的單位長向量。也就是說,$2$個量子比特對應到$4$維的希爾伯特空間、$3$個量子比特對應到$8$維的希爾伯特空間、$4$個量子比特對應到$16$維的希爾伯特空間等等。為什麼當我們增加量子比特的個數時,希爾伯特空間的維度是指數型成長呢?
這就跟希爾伯特空間的坐標系有關了!當我們擁有$2$個量子比特時,相對應的希爾伯特空間中,最自然會使用的坐標系將會是$\ket{00},\ket{01},\ket{10},\ket{11}$。其中$\ket{x_1x_2}$中的$x_1$對應到第一個量子比特的兩個坐標$0$或$1$,$x_2$對應到第二個量子比特的量個坐標$0$或$1$。以此類推,當我們有$n$個量子比特時,坐標系的坐標向量將會長得像$\ket{x_1x_2\cdots x_n}$,其中每個$x_i$的取值都是$0$或是$1$,於是總共會有$2^n$個不同的坐標向量,因此相對應的希爾伯特空間將會是$2^n$維。
量子比特和古典比特的比較: 量子比特和古典比特雖然在測量後的取值都是在0/1之間,然而由於量子比特在尚未被測量前可以具有相位,這不經讓人思考其是否可以存取更大的訊息量呢?讓我們直接說答案:雖然量子比特看似擁有更大(甚至可以說是無限大)的相位空間,然而我們可以讀取的訊息量其實並不會比古典比特可以給得多。具體來講,量子訊息和量子通訊中很重要的Holevo定理告訴我們量子比特其實並沒辦法比古典比特傳遞還要多的訊息量!
Holevo定理:$n$個量子比特,最多只能傳送$n$個比特的訊息量。
量子傳態(quantum teleportation)與量子超密編碼(superdense coding)更進一步展示了在擁有量子糾纏的情況之下,一個量子比特能夠存取的訊息量大約是兩個古典比特可以存取的訊息量。
量子傳態(Quantum teleportation):透過分享一對EPR pair和傳送兩個古典比特,便可以傳送一個量子比特。
量子超密編碼(Superdense coding):透過分享一對EPR pair和傳送一個量子比特,便可以傳送兩個古典比特。
不可複製定理(No-cloning theorem): 最後,量子訊息和古典訊息一個很大的不同就是,前者是不可複製的!在古典的世界中,由於讀取古典比特時並不會破壞其狀態,所以一旦知道這個古典比特的數值,我們就可以輕易地大量複製相同的古典比特。
然而,在量子的世界中,由於讀取量子比特將會迫使其坍縮至$\ket{0}$或是$\ket{1}$(根據波恩原則),於是我們並無法輕易地獲取一個量子比特完整的資訊(也就是它的震幅)。在數學上我們可以更進一步的證明,不存在一個方法可以在不知道量子態為何的情況下將其複製!
不可複製定理(No-cloning theorem):不存在一個方法可以在不知道量子態為何的情況下將其複製!
量子計算模型
建立好量子比特的概念之後,我們就可以開始討論如何在之上進行計算。
量子線路(Quantum circuit)與量子閘(quantum gate): 在之前的章節中,我們曾經學到了“線路”這一類的計算模型。雖然線路和圖靈機同樣都是一次只在少數幾個比特(或是所使用的符號)上做操作,然而線路會預先設定好要使用的操作是什麼,圖靈機則是根據當下的狀態來決定。
在量子計算的世界中,我們同樣能夠很自然地定義出相對應的量子線路模型以及量子圖靈機模型。然而,由於量子態在沒有被測量的情況下,可以進行的操作非常的局限(數學上來說,只能進行所謂的正夭轉換)。所以造成量子圖靈機的定義遠比古典的圖靈機還要複雜,使用上也比較不直覺。於是,人們便主要集中注意在量子線路上。
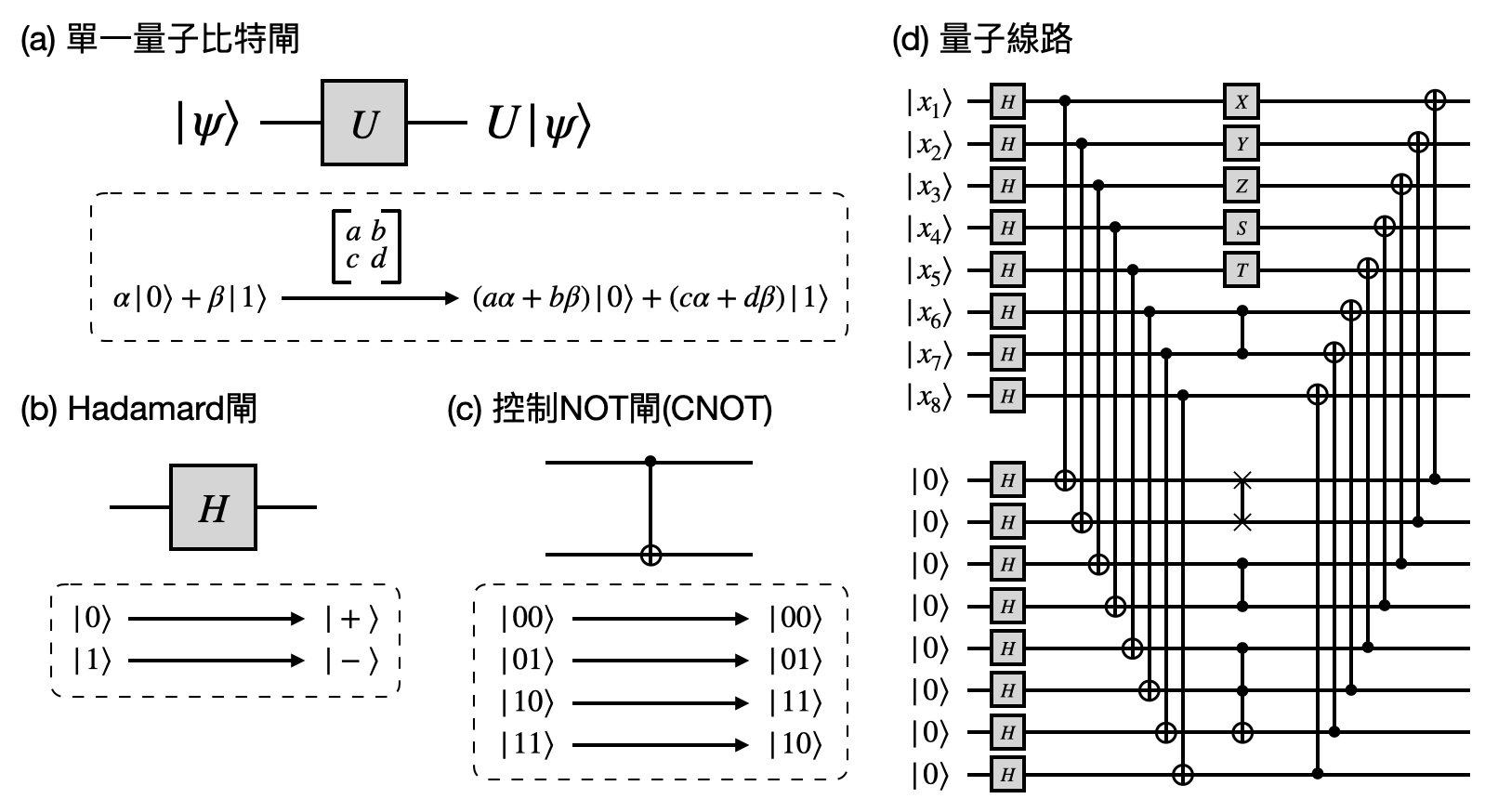
在量子線路中,基本的計算單元又被稱為量子閘(quantum gate),可以針對少數幾個量子比特做轉換。如上一段提到的,受限於量子力學的設定,量子閘必須符合特定數學型式,不能像古典的邏輯閘一樣可以是任意的函數。簡單來說,直覺上量子閘必須保存所有的訊息,而在數學上這對應到了所謂的“可逆性(invertible)”(或稱“么正性(unitary)”)。以下是幾個常見的量子閘(根據作用的量子比特個數分類)。
那我們是如何用量子線路做計算的呢?基本上可以被描述為以下三個步驟:
- 設計好量子線路。注意到一個量子線路的描述本身是個古典的訊息,也就是說可以用古典的電腦做設計和表示。
- 將計算問題實例的輸入準備成為一個量子態,並且接上量子線路相對應的輸入端。注意到通常我們還會在輸入端多加入一些被設置為全$0$的「輔助量子比特(ancilla qubit)」。
- 執行量子線路,並測量輸出端獲得一個輸出的量子態。如果是個決策型計算問題,我們通常就只會看第一個輸出的結果為何。
在不久後的段落中,我們會具體看到如何使用量子線路實現一些量子演算法,解決有趣的計算問題!
量子絕熱演化(Quantum adiabatic computing): 量子線路是個將古典線路量子化的計算模型,我們能否利用量子物理本身的演化方法來做計算呢?也許這在現實中更容易實現?量子絕熱演化就正是這樣的計算模型!
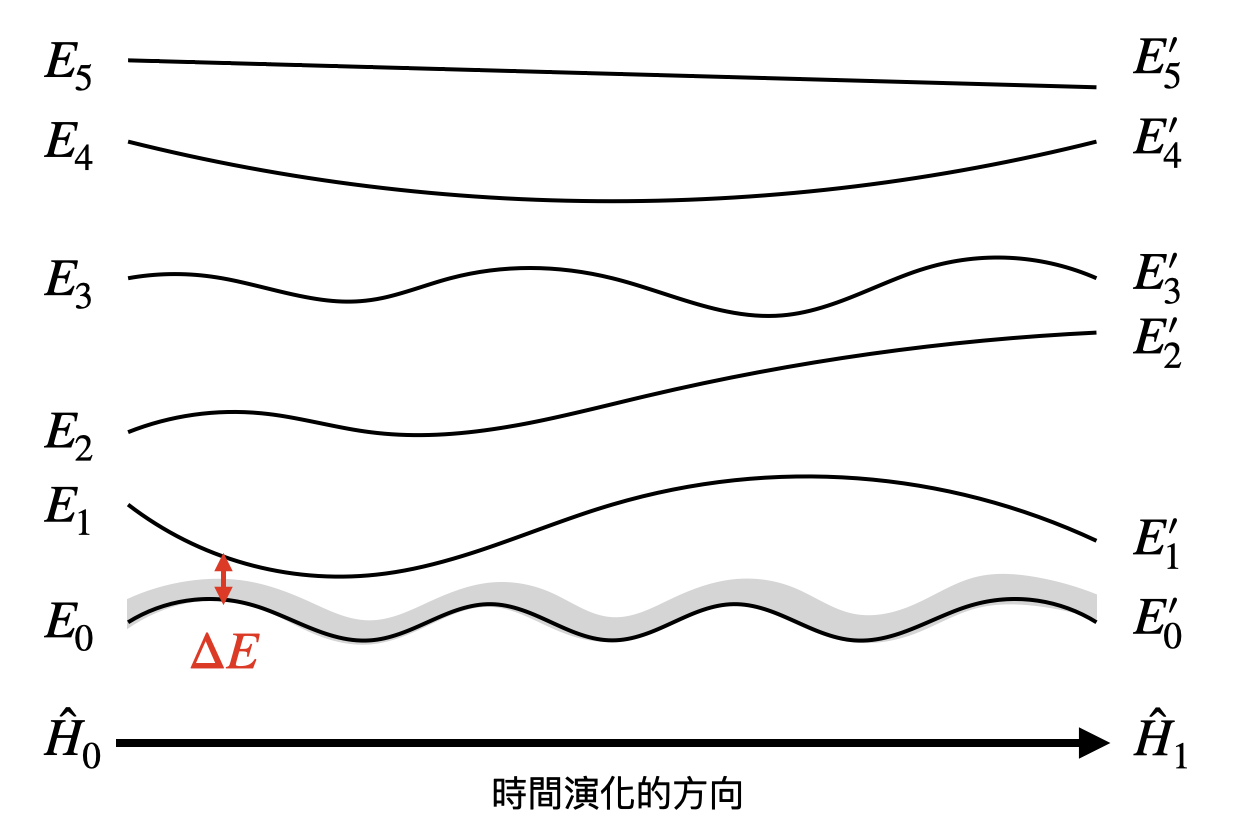
回顧一下,在薛丁格方程式$i\hbar\frac{\partial}{\partial t}\ket{\psi} = \hat{H}\ket{\psi}$中,我們看到了漢米爾頓算符$\hat{H}$扮演的重要角色。另外在路徑積分表述的段落中,我們也看到了量子態演化的疊加性。現在讓我們來考慮漢米爾頓算符的特徵態,並根據其特徵值的大小做排序。假如我們從一個漢米爾頓算符$\hat{H_0}$的基態(ground state, 也就是特徵值最小的特徵態)出發,並慢慢的把$\hat{H_0}$調成另外一個漢米爾頓算符$\hat{H_1}$,我們有沒有辦法讓這個量子態的演化是一直停留在基態呢?
如果可以的話,那麼我們將可以用以下的方式來做計算:將$\hat{H_0}$取為一個簡單的漢米爾頓算符,使我們很清楚地知道其基態為何。接著,根據想要解的計算問題,來設定$\hat{H_1}$,使得其基態為這個計算問題的解答。根據類似Cook-Levin定理的論述,這樣的計算方式是圖靈完備的!
不過這邊有個很關鍵的點:在從$\hat{H_0}$轉換到$\hat{H_1}$的時候到底需要多慢才能確保量子態的演化是一直停留在基態?量子絕熱演化定理(quantum adiabatic theorem)告訴我們這個轉換的速率將會和基態與第一個激發態的能隙(energy gap)有關,能隙越小,所需要的速率將會越慢。直覺上來說,如果移動太快的話,將會注入系統一些額外能量造成基態有可能被激發到其他的特徵態。這也是為什麼這樣的計算方式被稱為“絕熱演化”!
比較接近電腦科學的量子演算法
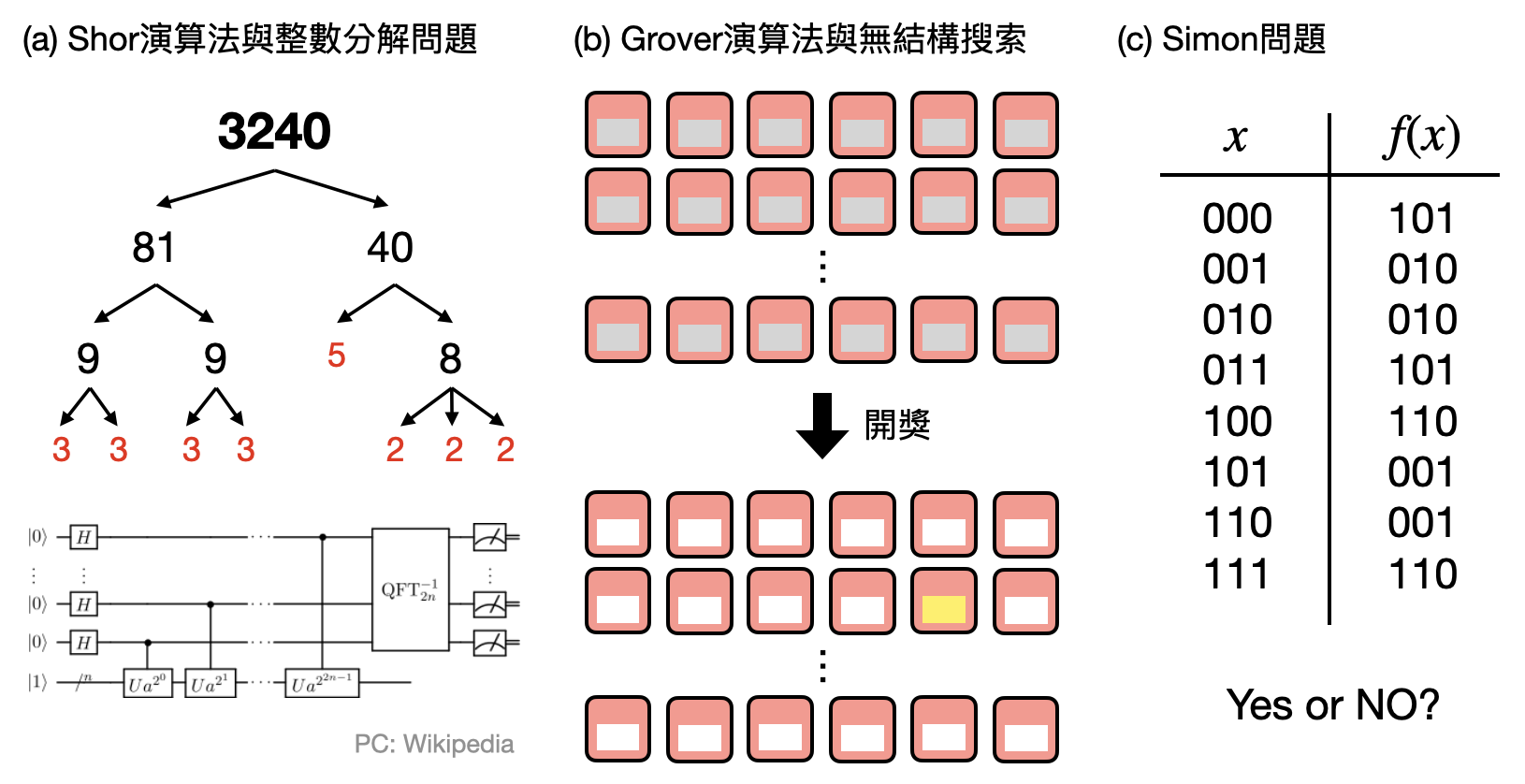
接下來,我們將看到兩個最常見的量子演算法:Shor演算法(Shor’s algorithm)和Grover演算法(Grover’s algorithm)。我們不會進入演算法的細節,而只會著重在講清楚這兩個演算法能夠做到的事情是什麼,以及澄清幾個常見的誤解。對於感興趣知道一些技術細節的讀者,我們將用和Shor演算法非常相關的Simon演算法,讓大家體會一下量子演算法設計和分析中的巧思。
Shor演算法(Shor's algorithm): 在之前的篇章中,我們看到了密碼學中的安全性是建立在假設某些計算問題是困難的。整數分解(integer factoring)問題和離散對數(discrete logarithm)問題是兩類在早期公鑰密碼學發展時常被拿來使用的計算問題。有趣的是,這些當年讓近代密碼學一飛沖天的計算問題,也是讓量子計算開始受到世人關注的推手!
不過雖然說是推手,實際上可能更像是個箭靶,因為量子計算中最著名的Shor演算法正是展示了量子計算在理論上可以在整數分解問題和離散對數問題提供指數的加速!也就是說,專家們一般相信這兩個計算問題在古典計算模型中並沒有多項式時間的演算法(甚至可能最快只能有接近指數時間的演算法),然而,Shor演算法卻可以在量子多項式時間內解決它們!這個在1994由Peter Shor提出的量子演算法,既是量子計算的重要里程碑,也容易被行外人誤用,所以在簡單介紹其背後的原理之前,先讓我澄清兩個重要的事實。
- 由於整數分解問題和離散對數問題都不是NP完全問題(但是它們都在NP裡面),所以Shor演算法並沒有説量子計算能夠給任何常見的計算問題加速。
- 實際上如果真的想要拿Turing演算法來破解現實生活使用的密碼系統,至少需要兩千顆(能夠糾錯的)量子比特,這個數字離目前(2023年)的科技還有些距離。
Grover演算法(Grover's algorithm): 在介紹Shor演算法時,我們強調了其核心概念利用到了整數分解和離散對數的代數結構,因此並不能對任意的計算問題加速。有趣的是,當一個(搜索型)計算問題毫無特殊結構時,Grover演算法告訴我們量子計算也可以提供一些簡單的加速!
還記得在和“複雜度下界”相關的章節中刮刮樂的例子嗎?假如彩券行發行了10,000張刮刮卡,但是只有一張是最大獎。如果想要確保有很高的機率能夠刮中最大獎,那麼基本上需要把這10,000張刮刮卡都試過才行。
那現在想像彩券行跟流行發行了一種量子刮刮樂,每次你要刮的時候,都可以選擇這10,000張刮刮卡的一個疊加態來刮。當你刮了一個疊加態時,你不會馬上知道結果,而是拿到了一個“被刮過的疊加態”,並且可以對這個態做一些操作之後再刮一次。在這樣量子的設定之下,Grover告訴我們,竟然可以有種量子刮卡方式,可以只要刮大約$\sqrt{10,000}\approx100$次就可以有高機率找到那個唯一的大獎!
注意到Grover演算法其實是個黑箱子(black-box)算法,它並不會利用到計算問題的結構(就像刮刮卡會不會中獎基本上是沒有結構的)。另外,它能夠提供的加速只有把“某個函數執行(例如刮卡)的次數”開根號而已。因此Grover演算法可能在實際上做不到太大的加速(畢竟將量子電腦從理論實現到現實的時候會有許多額外的消耗)。
最後,上述刮刮樂的例子只是為了提供讀者簡單的心理圖像,要講清楚什麼叫做“刮一個量子態”必須再多深入定義一些東西,因此在這邊可以暫時將刮一個量子態理解為,一旦知道怎麼刮普通的刮刮樂以及有了夠強的量子電腦後,就可以很容易做到的一件事情。所以在這個設定下,我們在意的計算資源是總共刮了幾次。
和Shor演算法一樣,Simon演算法也是針對某個計算問題的特殊結構來達到指數型的時間加速。不過Simon使用的問題就沒有像整數分解和離散對數那樣自然,他考慮的計算問題某種程度是個簡化版的整數分解問題(他們都是一種“隱藏子群問題(hidden subgroup problem)”),又被稱為Simon問題,定義如下。
現在有個未知的函數$f:\bit^n\to\bit^n$可以讓演算法詢問一個$n$量子比特的量子態$\ket{\psi}$,並且將函數的結果存在多餘的量子比特上。例如如果詢問的態是$\ket{x}\otimes\ket{0^n}$,那麼將會獲得$\ket{x}\otimes\ket{f(x)}$。Simon問題是要演算法透過越少越好的詢問次數,來分辨未知的函數$f$是屬於以下哪個類別的:
- Yes情況:存在一個非零的$s\in\bit^n$,使得每個$x\in\bit^n$,都有$f(x)=f(x+s)$,其中$x+s$指的是在每個比特上做二進位加法(也就是說$1+1=0$)。
- No情況:$f$會把每個不同的輸入$x\in\bit^n$都對應到不一樣的$f(x)$。也就是當$x\neq y$時,$f(x)\neq f(y)$。
Simon演算法分為三個步驟:
- 準備一個好用的疊加態$\ket{\psi_1}=\frac{1}{\sqrt{2^n}}\sum_{x\in\bit^n}\ket{x}\otimes\ket{0^n}$,這可以透過將Hadamard閘作用在前$n$個初始為$\ket{0^n}$的量子比特達成。
- 詢問$\ket{\psi_1}$,並且獲得$\ket{\psi_2}=\frac{1}{\sqrt{2^n}}\sum_{x\in\bit^n}\ket{x}\otimes\ket{f(x)}$。
- 將Hadamard閘作用在最後$n$個量子比特,並且獲得:
\begin{align*}
{\small \ket{\psi_3}} &= {\small\frac{1}{\sqrt{2^n}}\sum_{x\in\bit^n}\left[\frac{1}{\sqrt{2^n}}\sum_{y\in\bit^n}(-1)^{x\cdot y}\ket{y}\right]\otimes\ket{f(x)}}\\
&{\small= \frac{1}{2^n}\sum_{y\in\bit^n}\sum_{x\in\bit^n}(-1)^{x\cdot y}\ket{y}\otimes\ket{f(x)}}
\end{align*}
這邊$x\cdot y$指的是$x$和$y$的內積,也就是$x\cdot y=\sum_{i=1}^nx_iy_i$,其中$x_i$和$y_i$分別是$x$和$y$的第$i$個比特,而且式子中的加法是一個比特的二進位加法。
現在讓我們來分析一下在兩種不同的可能情況之下,最終的量子態$\ket{\psi_3}$會長什麼樣子:
- Yes情況:在這個情況下,存在一個特殊的非零$s\in\bit^n$,並且$f$可能的輸出值只有$2^n/2$種,讓我們用$\textsf{Im}(f)$來表示這個集合。對於每個$z\in\textsf{Im}(f)$,都恰有兩個$x_z,x_z’\in\bit^n$使得$f(x_z)=f(x_z’)=z$。不失一般性讓我們令$x_z$是其中排序比較小的那個,於是$f(x_z)=f(x_z+s)=z$。現在讓我們進一步把$\ket{\psi_3}$化簡如下:
\begin{align*}
{\scriptsize \ket{\psi_3}} &= {\scriptsize \frac{1}{2^n}\sum_{\substack{y\in\bit^n}}\sum_{\substack{z\in\textsf{Im}(f)\\\ f(x_z)=f(x_z+s)=z}}(-1)^{x\cdot y}+(-1)^{(x_z+s)\cdot y}\ket{y}\otimes\ket{z}} \\
&{\scriptsize = \frac{1}{2^n} \sum_{\substack{y\in\bit^n\\\ {\color{red}y}{\color{red}\cdot}{\color{red} s}{\color{red}=}{\color{red}0}}}\sum_{\substack{z\in\textsf{Im}(f)\\\ f(x_z)=f(x_z+s)=z}}2\cdot(-1)^{x_z\cdot y}\ket{y}\otimes\ket{z}} \, . \end{align*} 注意到,從第一行到第二行的過程中,一旦$y$和$s$內積為$1$,那麼所有$x_z$和$x_z+s$的相位都會互相消去掉!也就是說一旦我們測量$\ket{\psi_3}$的前$n$個量子比特,每次觀測到的$y$都會和$s$內積為$0$。
- No情況:在這個情況下,$f$的輸出值有$2^n$種可能,所以不會像情況Yes一樣出現互相消去的現象。對於每個$z\in\bit^n$,令$x_z$為$f(x_z)=1$的唯一解。因此,$\ket{\psi_3}$可以被化簡如下: \begin{equation*} \ket{\psi_3} = \frac{1}{2^n}\sum_{y\in\bit^n}\sum_{z\in\bit^n}(-1)^{x_z\cdot y}\ket{y}\otimes{z} \, . \end{equation*} 於是每次觀測$\ket{\psi_3}$前$n$個比特都會獲得完全隨機的$n$比特字串。
總結一下,Simon演算法利用到了Simon問題中獨特的數學結構,在準備量子態$\ket{\psi_3}$的過程中巧妙地將某些相位相消,使得在情況Yes的時候前$n$個比特的測量結果會透露隱藏字串$s$的訊息。因此只要重複整個過程$10n$次,就會有很高機率發現是否有隱藏字串,進而區分兩種不同的情況。反觀古典計算模型,我們可以證明對於任何演算法,都需要至少約$2^{n/2}$次的詢問才有可能高機率地解決Simon問題。雖然這個證明並不複雜,但仍然需要一些篇幅,感興趣的讀者歡迎參考延伸閱讀。
比較接近物理的量子演算法
雖然Shor演算法燃起了眾人對量子計算加速的希望,在現實中我們距離能夠實現Shor演算法還非常遙遠。主要的癥結點是在量子電腦實作中,各種物理和工程上的挑戰。因此,另外也有一群學者研究著如何用“比較物理”的方式來進行量子計算,也許和之前看到的演算法相比,這些比較接近物理的演算法比較有機會在不久的將來實現?
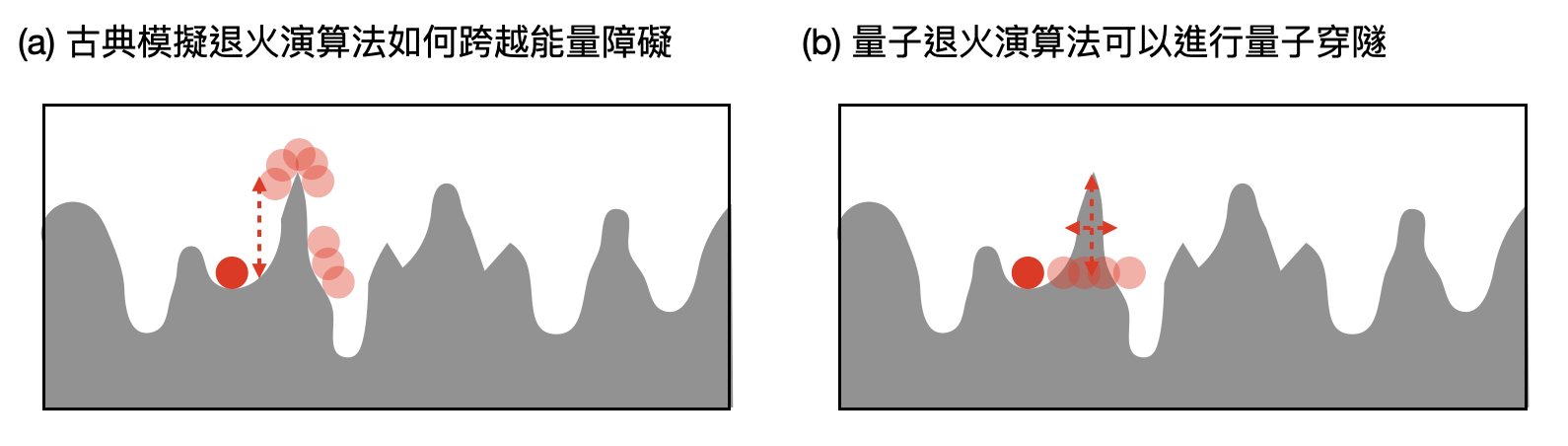
量子退火演算法與量子穿隧效應: 在關於統計力學的章節中,我們曾經看到“模擬退火演算法”是如何透過不同降溫速度調控的方式,來解決最佳化問題。同樣的想法也可以直接搬到量子世界來做,而且在某些情景下量子也許可以表現得更好!?
簡單回顧一下,在退火演算法中,我們想像在一個複雜的能量地貌上尋找最低點。當溫度高時,我們的移動速度比較快,因此較有可能攀爬比較高的能量障礙(energy barrier),進而跨越附近的高山。當溫度低時,則會減緩速度,趨向附近能量最小的地方。在古典的退火演算法中,跨越能量障礙所需的溫度是和能量差距成正比(如下圖(a))。然而對量子退火演算法來說,穿越能量障礙所需的溫度只和其“體積”相關(如下圖(b))。也就是說,如果眼前的能量高山薄薄地弱不經風,那麼量子退火演算法(quantum annealing)將可以輕鬆地直接向開隧道一樣穿過去。這也是為什麼大家將這個特別的性質稱為「量子穿隧效應(quantum tunneling effect)」。
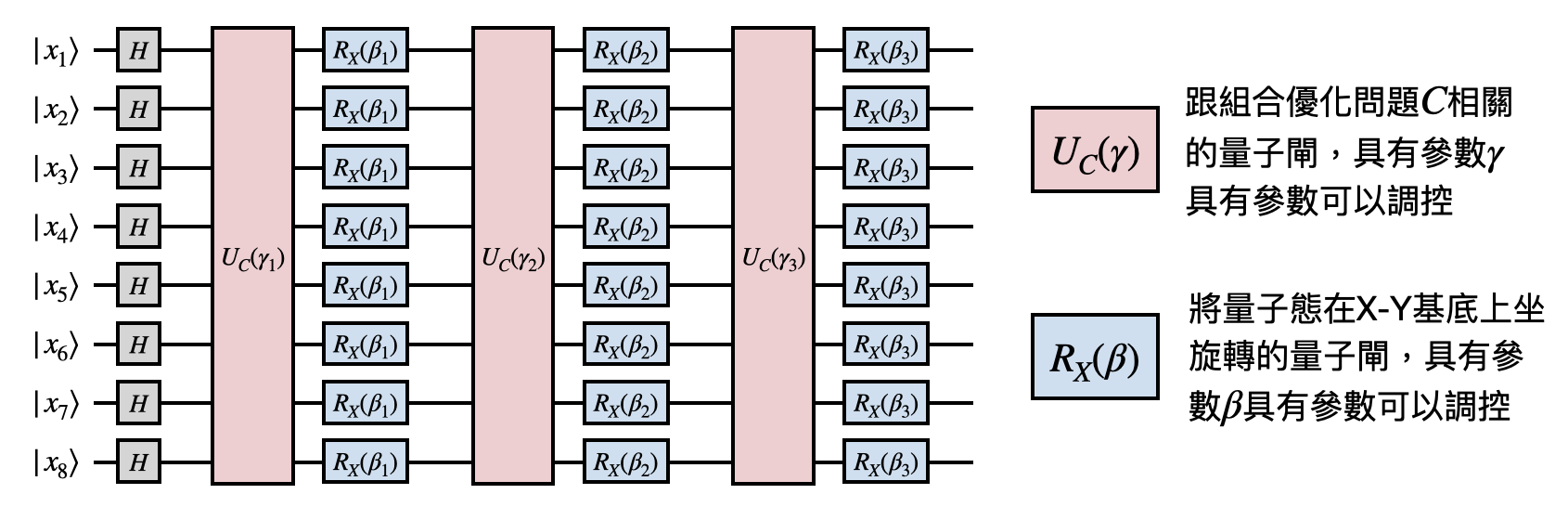
量子近似優化演算法: 量子退火演算法以及其他類似且偏向物理的量子演算法,都很適合在量子絕熱演化模型中實現。反觀之前看到的Shor演算法、Grover演算法等等,則是基於量子線路模型。有沒有什麼偏向物理(所以比較容易實作)又適合線路模型的演算法呢?
量子近似優化演算法(Quantum approximate optimization algorithm, QAOA)於2014年由三位在波士頓的物理學家Edward Farhi、Jeffrey Goldstone和Sam Gutmann提出,目標要在一些困難的組合優化問題(例如之前提到的計算最大切割問題)上,用量子線路模型表現得比某些古典計算模型還要好。和Shor演算法等很不一樣的地方在於,QAOA在理論上並沒有很明顯的量子計算優勢,然而其設計初衷讓它可以在很小規模且不完美的量子線路上就能夠實現。於是在很短的時間內QAOA就受到許多人的關注,最近還被許多開發量子電腦的團隊實現在小的組合優化問題上。不過,理論層面的劣勢讓QAOA更像是個時代背景下的練習曲,人們目前並不期待可以用QAOA做出超越古典電腦能做的事情。
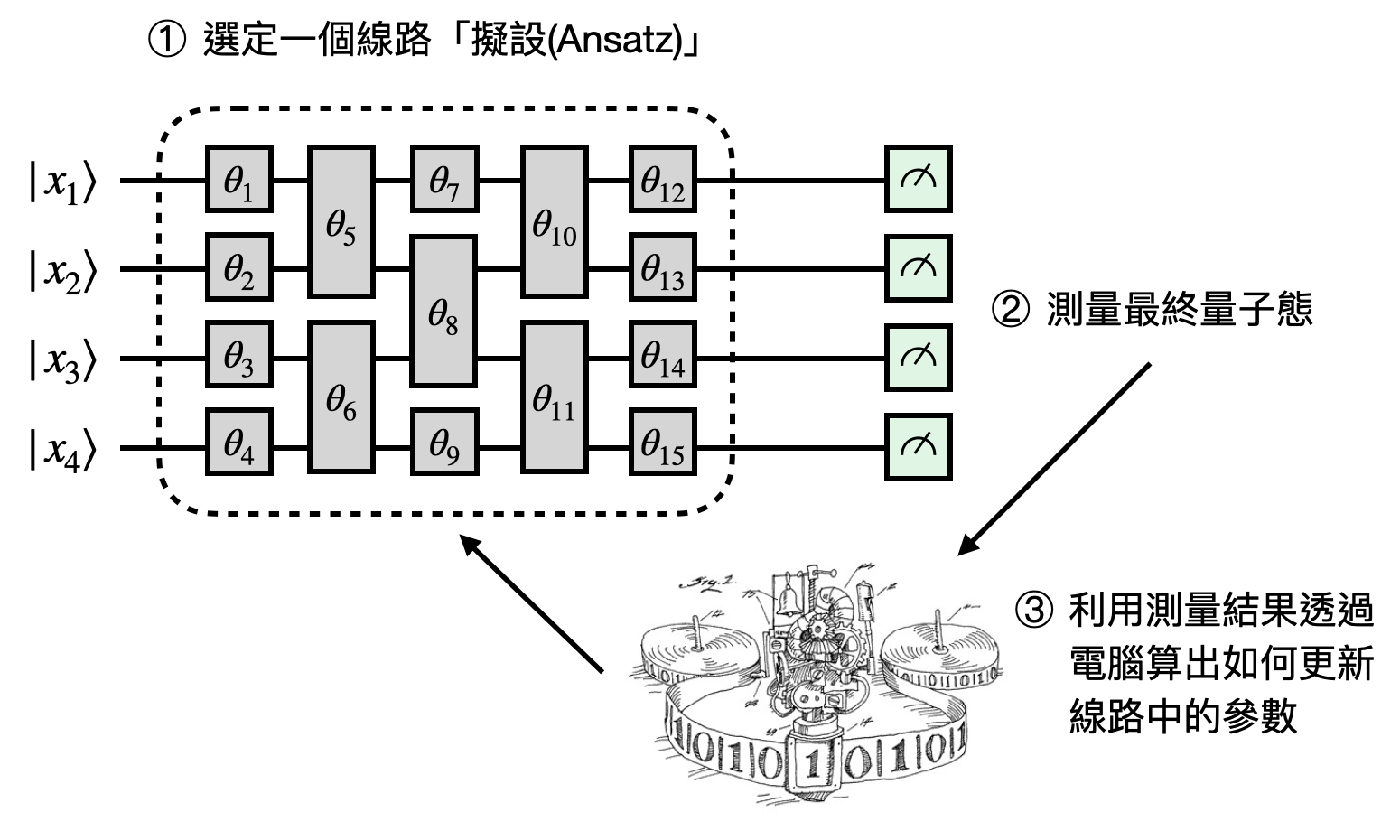
變分量子特徵態演算法: 和QAOA一樣想要在線路模型上能夠實現有用的量子計算,變分量子特徵態演算法(Variational quantum eigensolver, VQE)從組合優化問題轉換跑道,回過頭到物理中專注在考慮如何尋找一個漢米爾頓算符的基態。簡單回顧一下,漢米爾頓算符是用來描繪一個量子系統的物理模型,找到它的基態(能量最小的特徵態)就等於理解了系統在低溫時演化的終點。因此,在許多物理和化學的研究中,如果有個演算法能夠幫忙在數值上找到基態,就能幫助研究人員進一步理解所面對的複雜分子或系統。
VQE背後的概念很簡單:在量子線路中擺上許多“具有參數的量子閘”,每當固定參數後,並可以執行量子線路並獲取一個量子態。根據測量這個量子態來獲得一些資訊後,進一步更新線路中的參數。如此來回重複,直到拿到一個“很好”的量子態,或是計算資源用盡決定將演算法停下來。
因為容易上手,VQE在近年來被大量的在各種問題上面測試(在小型的量子電腦,或是一些用古典電腦做的數值模擬中),甚至和機器學習都沾上邊。不過VQE和其他物理出發的演算法(退火演算法、QAOA等等)一樣,偏向依靠經驗法則,並沒有太多理論上面嚴格的解釋和分析其表現成效。
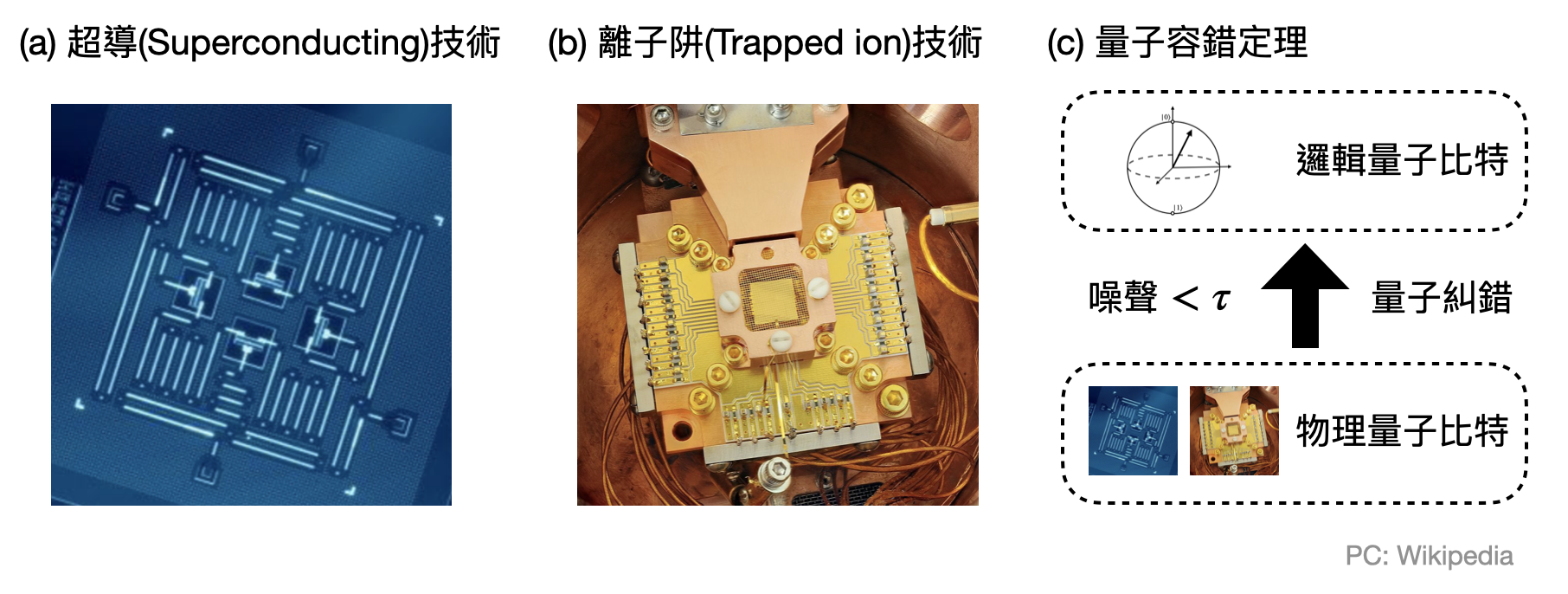
量子電腦的實作與量子容錯定理
看了這麼多關於量子計算的紙上談兵,讀者們應該已經忍不住想問到底量子電腦的實作情形到底如何?什麼時候可以看到量子電腦的成功呢?
現階段有許多基於不同物理/工程技術的量子電腦實作(如下圖(a)),各有各的優越點。但如果拿來和古典電腦發展的歷史相比,量子電腦現在大概還在40到50年代時的真空管電腦或甚至更早的階段。雖然許多實驗室已經可以實現數十數百至破千個量子比特,但是這些量子比特都是所謂的「物理量子比特(physical qubit)」,受到來自實驗儀器或是不明來源的噪聲影影響,因此可能會出現不在預期內的行為。而之前學到的演算法(尤其是接近電腦科學的演算法)都是基於所謂的「邏輯量子比特(logical qubit)」,也就是完美無瑕能夠自由進行各種數學操作的量子比特。
在「量子容錯定理(quantum fault-tolerance theorem)」中,理論學家證明了一旦能夠將物理量子比特的噪聲降至某個程度以下,那麼就可以依靠量子糾錯(quantum error correction)的技術系統性地將物理量子比特轉換成邏輯量子比特,進而將理論與實務接軌。不過,這些量子容錯的技術目前在理論上使用了非常多的物理量子比特,所以鵲橋出現的那一刻也許還需要再等一段時間。
總結
量子世界的發現源於物理學家對微觀現象無止境的好奇,隨後應運而生的物理模型更是帶來極為豐富的數學結構,並且給了人們對於新型計算模型的期待。不知道五十年後回頭看時,我們會讚嘆於這些理論演算法的先知灼見,還是已經對量子計算有了全然不同的理解?
延伸閱讀
教科書與其他教材:
- J. Sakurai and J. Napolitano. Modern Quantum Mechanics (3rd ed.). Cambridge: Cambridge University Press, 2020.
- M. A. Nielsen and I. L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition (10th. ed.). Cambridge University Press, 2011.
內文提及的論文:
- J. S. Bell. On the Einstein Podolsky Rosen paradox. Physics Physique, 1964.
- P.W. Shor. Algorithms for quantum computation: discrete logarithms and factoring”. Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. Press, 1994.
- D. Aharonov and M. Ben-Or. Fault-Tolerant Quantum Computation with Constant Error Rate. SIAM Journal on Computing, 2008.
- E. Knill. Resilient Quantum Computation. Science, 1998.
- A. Kitaev and Yu. Fault-tolerant quantum computation by anyons. Annals of Physics, 2003
科普書籍:
- S. Aaronson. Quantum Computing Since Democritus. Cambridge University Press, 2013.