第5章

由上而下的現象學：統計物理

Statistical mechanics is extremely easy and it’s extremely hard. It’s subtle. It’s fulled of surprises. It’s fulled of the applications of very simple formulas which then yield extremely surprising and powerful results.

統計力學非常簡單同時也極度困難，它很微妙且充滿驚喜，裡頭充滿著簡單乾淨的公式，且總是能找到廣泛的應用並獲得令人驚豔和強大的結果。

Leonard Susskind

雖然古典力學提供了一個強大完整的理論，讓人們可以系統性地建立物理模型來描繪一個系統。然而，混沌現象告訴我們即使有模型在手，也不代表可以方便地使用它做出有用的預測。甚至當系統只有三個物體時，混沌現象就已經可以把物理學家搞得暈頭轉向了。難道物理學的研究就這樣卡關了嗎？

統計物理

統計物理(Statistical physics)的目標是要在當系統中物體數量龐大時，縱使無法仔細追蹤所有的細節，仍然希望能夠在宏觀層面上提供一些有用的物理理解。同時，統計物理在歷史上的的發展又和熱力學(Thermodynamics)有著密不可分的關係，許多基礎概念都是先在熱力學的設定之下被發現和定義清楚的。於是，我們將會大量地運用熱力學的例子和直覺來建構各種重要觀念。

本章的結構約略可以分為三大部分。我們將從熱力學的角度出發，學習能量、熱平衡和系綜等等的概念，最終見識到Boltzmann分佈(或稱為Gibbs分佈)是如何自然地出現，並成為統計力學模型中的骨幹。接著，我們將以經典的Ising模型作為模板，展示在第一部分中推導出來的世界觀可以如何在簡單的數學模型中展現豐富的物理性質。最後，我們將看到許多統計力學和計算互相影響與成長的故事。

宏觀狀態與微觀狀態

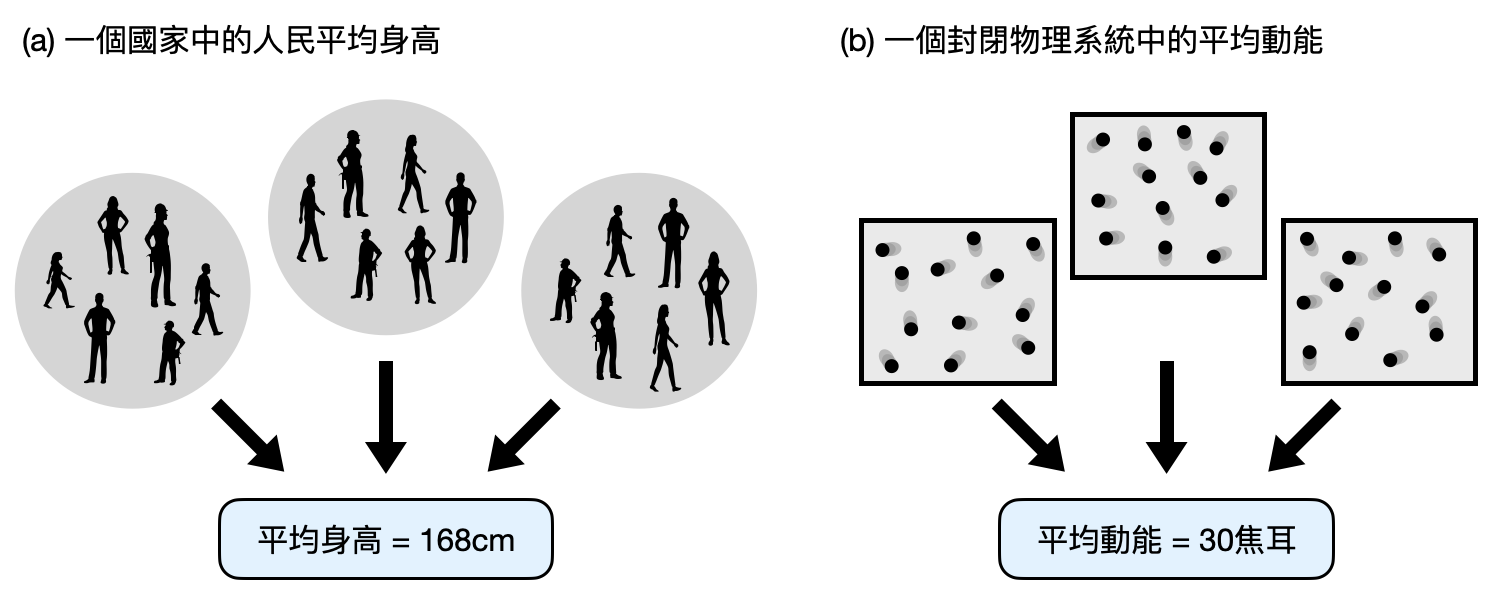
如果要測量一個國家中人民的平均身高，你會怎麼做？我相信沒有人會真的把每個民眾的身高都搜集起來再取平均，最常見的做法大概會是隨機選個幾百幾千人，然後從他們的身高中取平均作為一個估計值。國家的平均身高就像是國家這個系統的一個宏觀狀態(macrostate)，而每個人民具體的身高整合起來則是一個微觀狀態(microstate)。從這個例子中，我們可以觀察到，想要知道宏觀狀態為何，並不一定要完全掌握微觀狀態中的細節。這就是統計物理的核心理念。

統計物理：理解系統的宏觀狀態不見得需要知道微觀狀態的細節。

以比較物理味道的例子來說，假設一個系統中有$N$個粒子跑來跑去。古典力學理論告訴我們，當粒子的質量為$m$速度為$v$的時候，它的動能會是$mv^2/2$。假如系統中有$N$個粒子，且第$i$的粒子的質量是$m_i$速度為$v_i$，這時候，系統中所有粒子確切的位置和速度是系統的微觀狀態，而整個系統的平均動能$\frac{1}{N}\sum_{i=1}^Nm_iv_i^2/2$，則是系統的一個宏觀狀態。當系統中粒子數量足夠多，且沒有太奇怪的表現時，平均動能將會是個很容易測量且穩定的可觀測量(observable)。

(a)宏觀狀態：一個國家的平均身高、一個系統的動能。(b)微觀狀態：一個國家中每個人民各自的身高、所有粒子確切的位置和速度。

更多宏觀狀態的例子諸如氣溫、密度、磁矩等等，都是些在日常生活及物理討論中常聽見的概念。那該用什麼方式來理解宏觀狀態和微觀狀態的關係呢？

如前面強調的，不同微觀狀態很有可能會擁有相同的宏觀狀態。也就是說，當觀測到一個宏觀狀態時(例如氣溫為28度C)，實際上可能會有數以萬計的微觀狀態都符合這個宏觀狀態。統計物理名稱中的“統計”，就是指利用數學上的機率分佈來刻畫無法具體觀測到的微觀狀態，並且將系統中的宏觀可觀測量定義為這個機率分佈的統計量。

由於無法直接觀測到微觀狀態，在統計物理中我們用機率分佈來刻畫微觀狀態出現的比例/機率。

那微觀狀態是根據什麼機率分佈呢？為什麼系統的宏觀狀態能夠被穩定地測量出來呢？

首先，我們只會在意和實際物理相關的機率分佈，也就是在一些合理的物理情景之下推導出來的機率分佈。再來，我們會希望系統在宏觀層面達到某種「平衡(equilibrium)」，如此一來每次實驗測出來的宏觀觀測量才會非常接近。例如將一個公平的骰子擲了非常多次後，正面出現的比例將會趨向50%。於是，一旦我們能夠把“平衡”這個概念定義清楚，就能推導出微觀狀態的機率分佈，並進一步開始系統性地對宏觀狀態進行測量和研究。

所以平衡到底是什麼意思呢？讓我們先從「能量(energy)」和「熵(entropy)」這兩個關鍵概念說起。

能量與熵

在金融世界中，錢是一切的最基礎單位。每個人之間的互動、交易都是建立在錢的交換之上。整個社會的各種整體指標也都可以從金錢的分佈來推算出來。而在這個肉弱強食的世界中，俗話說富不過三代，沒有永遠的有錢人，金錢總是不停地流動，人們在不斷賺錢和花錢中消磨了歲月。

在物理世界中，能量就像是每個粒子的錢(只不過對於粒子來說它們比較希望能量低一點)，而財富分配的平均程度則可以被熵給量化。不過譬喻終究是譬喻，感興趣的讀者可以往下看看能量和熵背後的物理及數學含義。

能量(Energy) 是封閉物理系統中的守恆量(之一)，於是很自然地成為了定義何謂平衡時的關鍵角色。在物理上，大家可能聽過各種類型的能量，諸如動能、位能等等。但現在讓我們暫時拋開這些過去的物理直覺，從數學的角度來看看能量是什麼。

在數學上，能量是個將微觀狀態對應到某個數值的函數。一旦為系統定下了能量函數之後，基本上等同於設定好這個系統所有的基本物理性質，就如在古典物理中設下了拉格朗日量或漢米爾頓量一樣。直覺上，能量是個將微觀狀態依宏觀世界觀點分類時，最細微的尺度。也就是說，所有在物理實驗中可以測量和感興趣的宏觀測量值，都可以從能量推導出來。

能量是個封閉系統的守恆量、系統之間交換的最小單位以及宏觀世界中最細微的尺度。

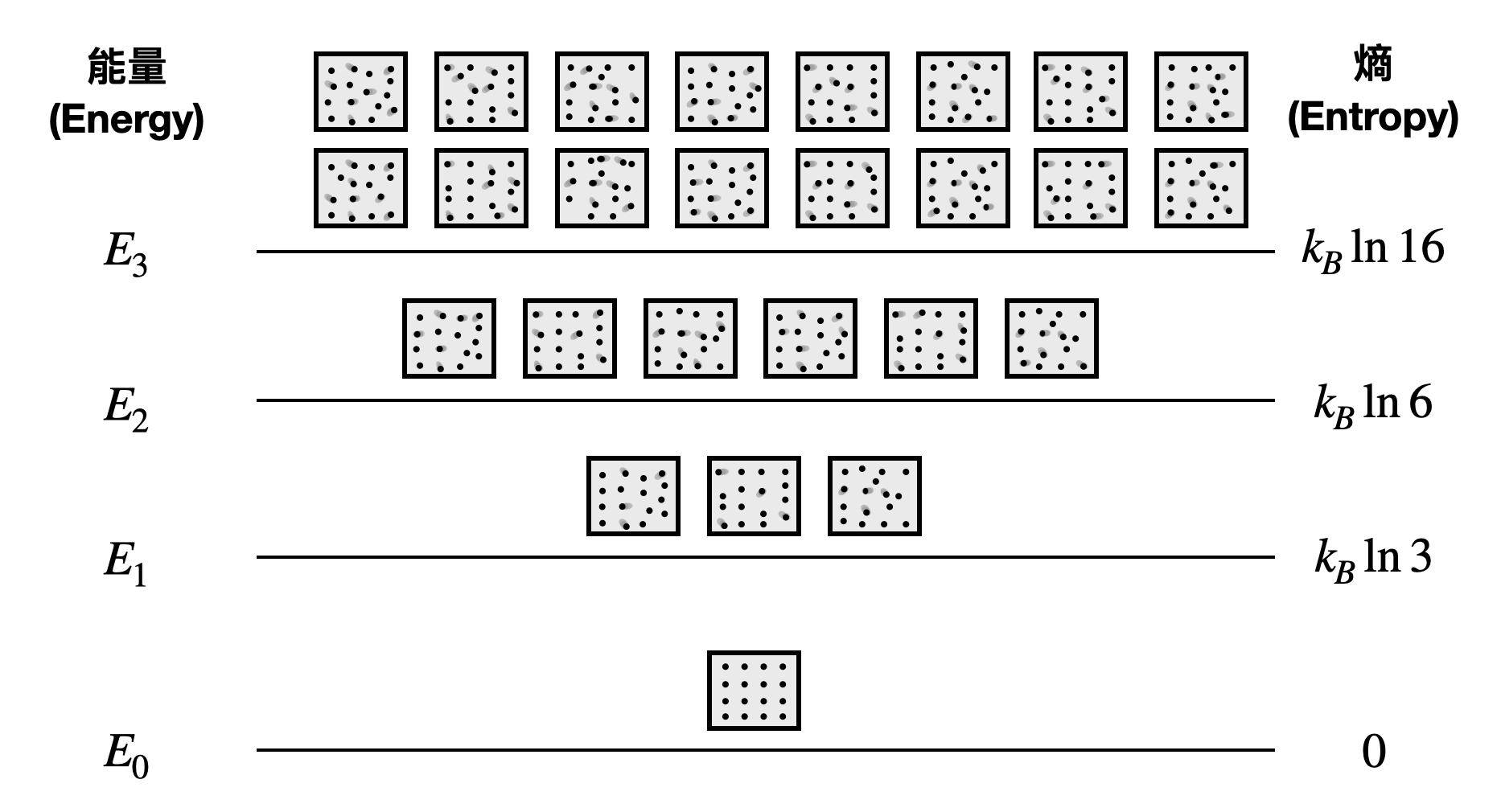
能量本身也是個宏觀觀測量，會有許多微觀狀態具有相同的能量值。當一個系統具有能量$E$的時候，對應的微觀狀態個數通常會被標示為$\Omega(E)$。當現在系統不處於單一能量，而是在不同能量之間改變轉換時，該如何定義能量呢？假設我們對於系統所處的能量有個機率分佈${p_i}$的刻畫，也就是說，有$p_i$的比例/機率會擁有能量$E_i$。這時候，系統的“平均能量”將會被定義成期望值$\mathbb{E}[E_i]=\sum_ip_iE_i$。

熵(Entropy) 是個描述一個系統有多混亂以及多接近“平衡”的數值，當熵越大代表系統越混亂，熵越小則代表系統包含比較低的信息量。在不同的地方，會有許多看似稍微不一樣關於熵的具體定義。而在熱力學和統計力學中，從第一原理出發的定義會是如下：對於一個具有能量值$E$且達到平衡的系統來說，它對應的熵被定義為

\begin{equation*} S(E)=k_B\ln\Omega(E) \end{equation*} 其中$\ln\Omega(E)$指的是將$\Omega(E)$取自然對數，$k_B$則是所謂的Boltzmann常數(Boltzmann constant)，它確切的數值對於接下來的討論沒有很重要。

和平均能量的定義類似，當我們對系統所處的能量有個機率分佈${p_i}$的刻畫時，系統的熵將會被定義成期望值$\mathbb{E}[S_{E_i}]=\sum_ip_iS_{E_i}$。

為什麼在熵的定義中要取(自然)對數呢？在直覺上，當考慮兩個互相獨立的系統$A$和$B$時，我們會希望整體的熵值是各自熵的和，也就是說$S=S_A+S_B$。於是乎，對數函數很自然地成為了一個方便的選擇。同時，如此定義熵的數學選擇，也讓後續統計力學以及其他領域的發展，深受其豐富的數學性質所滋潤。關於熵的最後一個小澄清是，熵不是個宏觀狀態(因此之後我們會看到這讓計算熵是件困難的事情)。

通常物理學家會用“能階圖”來視覺化一個系統的能量函數。圖中每條線對應到了一個可能的能量值，並且由小到大從下到上排列，整體的分佈被稱為能階。最小的能量值通常被稱為「基態(ground state)」。圖中每條線上方對應到了具有此能量的微觀狀態。

了解統計物理中的能量和熵到底是什麼後，我們就可以來討論系統的平衡是什麼了。根據考慮的物理情境的不同，相對應關於平衡的定義可能也略有差異。在熱力學中，我們使用了系綜(ensemble)的概念來訂下幾種常見的物理情境以及相對應的平衡。

系綜與平衡

對一個系統來說，通常會有無數個微觀狀態對應到相同的宏觀狀態。想像當一個國家的總資產是固定的時候，有多少種可能的財富分配方式？會是有某個富翁拿走了絕大多數的錢，還是人人財富平等？又或是財富的分配是在某些微觀狀態中不停轉換，且同時感興趣的宏觀觀測量是很穩定的？我們該如何在如此無法確定微觀狀態為何的清況之下，從實驗結果中獲得有用的資訊，進一步做有用的分析和實驗設計呢？

統計物理的一個核心概念，就是讓我們不再從單一微觀狀態這個角度來思考，而是把所有吻合宏觀狀態的微觀狀態們聚集起來，看成是一個「系綜(ensemble)」。以下這個思想實驗可能可以讓讀者更快感受到系綜的概念：假想你每天上班的路上都會順路去附近的港點店買蛋塔，他們家的師傅特別厲害，做出來的蛋塔每次吃起來都一樣好吃(宏觀測量值都是一樣的)。同時你每次都會用實驗室的神秘儀器測量蛋塔的所有原子細節(微觀狀態)，沒有很意外的，每天蛋塔的原子細節都不太一樣。在這個例子中，港點店的師傅就像是定義了一個蛋塔系綜，隨著你吃的蛋塔越來越多，蒐集到的資料逐漸給了你系綜下蛋塔原子細節的機率分佈。有了這個機率分佈，你便可以做進一步的分析和研究，例如平均加入的糖是多少克或是平均的熱量是多少卡。

言歸正傳，讓我們回到正經的物理場景設定。根據實驗中不同的環境設計，我們可能會將不同的微觀狀態納入考量，而最簡單的環境設計就是讓系統處於某種「平衡(equilibrium)」。雖然平衡一詞在直覺上聽起來很有感覺，但在數學上該如何定義呢？在一般統計物理和熱力學的討論中，有三種常見的(思想)實驗環境設定，對應到三種不同的系綜以及相對應的平衡。

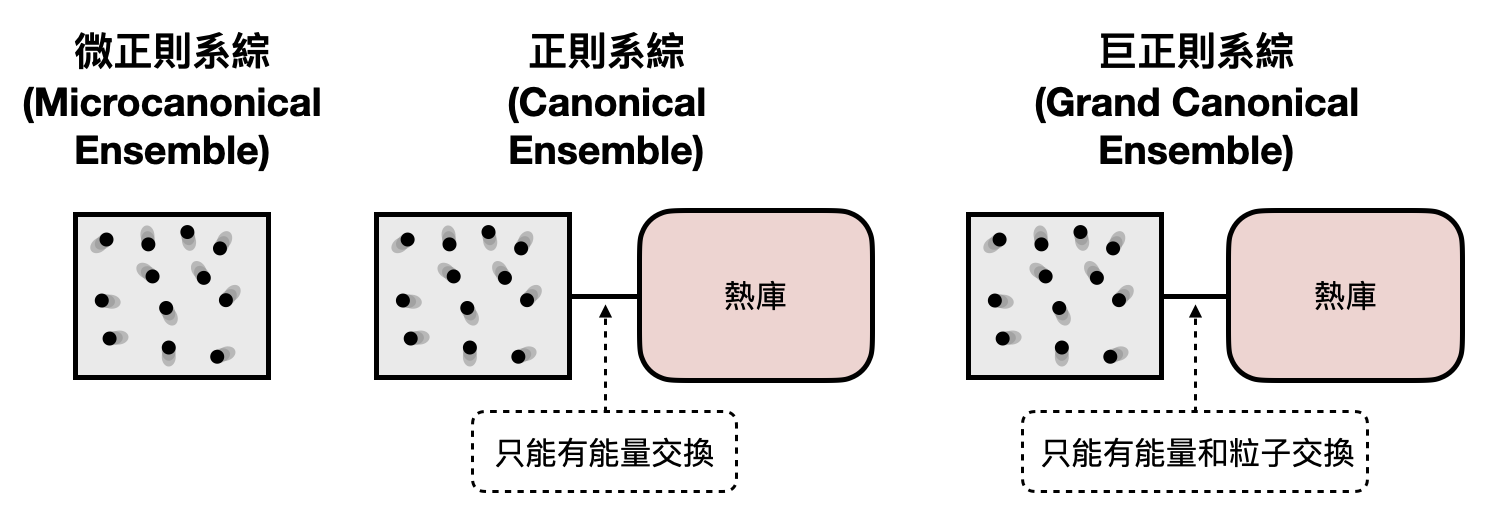
微正則系綜(Microcanonical ensemble)：考慮一個與世隔絕的物理系統，無法和系統外做任何互動與交換。也就是說，所有可能出現的微觀狀態將會具有相同的能量。於是，很直覺的，熱力學將微正則系綜中的平衡定義為當以下兩個基礎假設成立時的狀態：(1)等機率原則(Postulate of Equal a Priori Probabilities)：當系統具有能量$E$時，每個具有能量$E$的微觀狀態都有同樣的出現機率。(2)遍歷性假設(Ergodic Hypothesis)：當系統具有能量$E$時，會不斷地在各個具有能量$E$的微觀狀態之間轉換，而且每個微觀狀態所待的時間是一樣多的。

等機率原則(Postulate of Equal a Priori Probabilities)：每個具有相同能量的微觀狀態擁有同樣的機率。

遍歷性假設(Ergodic Hypothesis)：達到平衡之後，系統會遍歷所有具同樣能量的微觀狀態，且在每個微觀狀態待一樣多的時間。

正則系綜(Canonical ensemble)：考慮一個封閉但是能和穩定的熱庫(thermal reservoir)交換能量的物理系統。由於可以和熱庫做能量交換，一個系統的能量不再是一個固定的數值，只有系統的“平均能量”是固定的。這時候，熱力學就將平衡定義為系統達到最大熵時的狀態，這樣的平衡又被稱為熱平衡(thermal equilibrium)。從微正則系綜的平衡定義中，我們知道對於兩個具有相同能量的微觀狀態來說，它們出現的機率是相同的。那對於兩個具有不同能量的微觀狀態來說，它們出現的機率有什麼不同呢？我們將在下一個小章節做更深入的探討。

最大熵原則(Principle of Maximum Entropy)：當系統達到熱平衡時，將會達到(同樣平均能量中)最大的熵值。

巨正則系綜(Grand canonical ensemble)：考慮一個封閉但是能夠和熱庫交換能量和粒子的物理系統。由於粒子不平均的分佈將會產生所謂的化學勢(chemical potential)，在定義巨正則系綜的平衡時，需要在熱平衡之上多加考慮這一個因子。不過在數學結果上其實沒有太大本質上的不同，因此本書的討論將著重在正則系綜的熱平衡。

正則系統中的熱平衡與溫度

之前提到了能量是一個封閉物理系統的守恆量，而當我們考慮一個開放且與環境有交互作用的物理系統時，能量便會開始在不同的子系統之間交換。也就是說，即使整個系統達到了平衡，子系統的能量還是會有些許震盪，只有在(時間或/和系綜)平均上是固定的。

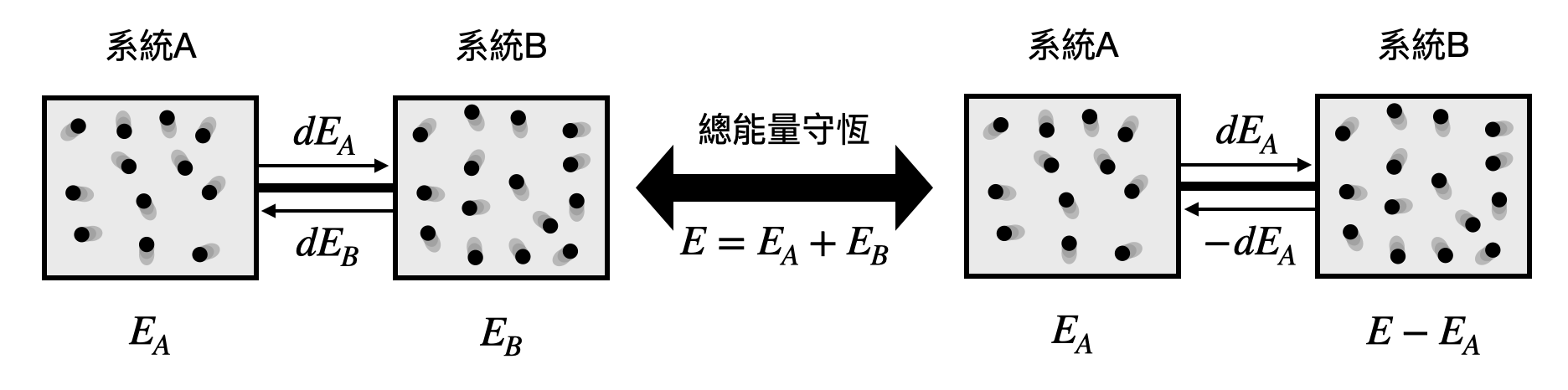
讓我們考慮兩個相連且只能做能量交換的系統$A$和$B$，並把它們的能量標記為$E_A$和$E_B$。首先，整體能量$E=E_A+E_B$是守恆的。接著，當系統達到熱平衡(thermal equilibrium)時，子系統$A$的能量變化$dE_A$和子系統$B$的能量變化$dE_B$會相互補，也就是$dE_A=-dE_B$。在這邊$d(\cdots)$對應到的是考慮$(\cdots)$的微小變化。在數學上，熱平衡的條件限制了這兩個子系統之間能量交換的速率要一樣。但是，這並沒有告訴我們速率的大小為何。我們還需要另一個額外的參數來顯示能量交換的速率！沒錯，這個參數就是溫度(temperature)。

從平常生活的語境來說，當溫度越高的時候，能量的交換速度是越快的。該如何將這個直覺和統計力學中的原則聯繫起來呢？

讓我們來看看最大熵原則可以進一步給出什麼限制條件。當整個系統的能量為$E$、子系統$A$的能量為$E_A$、子系統$B$的能量為$E_B=E-E_A$時，我們知道整個系統的微觀狀態數量將會是$\Omega(E_A)\times\Omega(E_B)=\Omega(E_A)\times\Omega(E-E_A)$。最大熵原則告訴我們系統會在熵最大時達到平衡，經過一些標準的數學推演(詳見稍後的延伸內容)，我們會得到 \begin{equation*} \frac{d\ln\Omega(E_A)}{dE_A}=\frac{d\ln\Omega(E_B)}{dE_B} \, . \end{equation*}

由於子系統$A$的熵為$S_A=k_B\ln\Omega(E_A)$，上面的公式等價於 \begin{equation*} \frac{dE_A}{dS_A}=\frac{dE_B}{dS_B} \, . \end{equation*} 也就是說，當整體系統達到熱平衡時，各個子系統中能量對熵的變化率($dE/dS$)是固定的！這個變化率恰恰回答了先前對於能量變化速率該如何表示的煩惱，我們可以將溫度定義為能量相對於熵的變化速率！嚴格來說，我們會定義溫度$T$使得$k_BT=\frac{dE_A}{dS_A}$。直覺上，溫度乘上Boltzmann常數之後(也就是$k_BT$)就像是能量和熵之間的匯率，告訴了我們想要把系統增加一單位的熵時，需要加入多少的能量！

沿用上述的設定和符號，整體系統的能量為$E$，系統$A$的能量為$E_A$，系統B的能量為$E-E_A$。如果整體系統處在最大熵的狀態，總熵值$\ln(\Omega(E_A)\times\Omega(E-E_A))$對能量改變$dE_A$的微分會是$0$： \begin{equation*} \frac{d\ln(\Omega(E_A)\times\Omega(E-E_A)}{dE_A}=0\, . \end{equation*} 根據對數函數的性質、$E_B=E-E_A$和$dE_B=-dE_A$，我們得到 \begin{align*} &\frac{d\ln(\Omega(E_A)\times\Omega(E-E_A)}{dE_A} \\
=& \frac{d(\ln\Omega(E_A)+\ln\Omega(E-E_A)}{dE_A}\\
=& \frac{d\ln\Omega(E_A)}{dE_A} + \frac{d\ln\Omega(E-E_A)}{dE_A}\\
=& \frac{d\ln\Omega(E_A)}{dE_A} - \frac{d\ln\Omega(E_B)}{dE_B} \, . \end{align*} 如前所述，最大熵原則要求上式為0，於是我們得到正文中提到的$d\ln\Omega(E_A)/dE_A=d\ln\Omega(E_B)/dE_B$。

Boltzmann分佈/Gibbs分佈

如果要請物理學家選一個統計物理中最重要的概念，那很高的機會聽到的回答會是：Boltzmann分佈(Boltzmann distribution)，或有些人會稱其為Gibbs分佈(Gibbs distribution)。沒錯，Boltzmann分佈正是物理學家拿來研究系綜中微觀狀態的機率分佈。在這邊讓我們直接切入具體的數學定義，以及如何解讀和使用Boltzmann分佈。在之後的延伸內容中我們會看到如何從正則系綜中推導出Boltzmann分佈。

當一個正則系統的溫度為$T$且達到熱平衡時，一個具有能量$E$的微觀狀態出現的機率將正比為$e^{-E/k_BT}$。例如，對於一個具有能量$E_i$的微觀狀態，Boltzmann分佈告訴我們系統處在這個微觀狀態的機率可以被寫成 \begin{equation*} \frac{1}{Z}e^{-E_i/k_BT} \end{equation*} 其中$Z$是個將機率調整為加起來恰恰為$1$的歸一化常數(normalizing constant)，又被稱為配分函數(partition function) \begin{equation*} Z = \sum_i\Omega(E_i)e^{-E_i/k_BT} \, . \end{equation*}

於是，往後統計力學中的研究基本上可以被整理為以下兩個步驟：

統計力學的世界觀：(1)定義一個系統的能量函數，(2)分析相對應的Boltzmann分佈和配分函數。

最後，讓我們用個關於名稱的小小澄清作結：Boltzmann分佈又時常被稱為Gibbs分佈，而另外還有一個機率分佈叫做Maxwell-Boltzmann分佈(Maxwell-Boltzmann distribution)。後者是前者在理想氣體中的一個特例。會有這些很相似的名稱，主要是因為Ludwig Boltzmann(1844-1906)、Josiah Gibbs(1839-1903)和James Maxwell(1831-1879)這三人都對熱力學和統計力學的基礎有著奠基性的貢獻。許多人在剛開始學統計物理的時候，常常被各種名詞搞昏了，希望讀者們不會受到這樣的困擾！

在正則系綜中，我們將熱庫想像成一個遠比所關注的子系統$A$還要巨大的系統，並且兩者的整體能量為$E$是個守衡量。現在我們將子系統的能量$E_A$視為變數，並想要知道當溫度固定為$T$時，$E_A$的機率分佈會長什麼子。

首先，子系統的能量為$E_A$的機率會正比於整體的微觀狀態數量，也就是 \begin{equation*} \Omega(E_A)\times\Omega(E-E_A) = \Omega(E_A)\times \exp(\ln\Omega(E-E_A)) \, . \end{equation*} 由於$E$遠比$E_A$大，所以我們可以用Taylor近似法將$\ln\Omega(E-E_A)$近似為$\ln\Omega(E)-E_A\times d\ln\Omega(E)/dE$。你沒看錯，$d\ln\Omega(E)/dE$根據之前對溫度的定義，就恰恰是溫度乘上Boltzmann常數後的倒數！於是我們得到 \begin{align*} \exp(\ln\Omega(E-E_A)) &\approx \exp\left(\ln\Omega(E) -\frac{E_A}{k_BT}\right) \\
&= \Omega(E)\times \exp\left(-\frac{E_A}{k_BT}\right)\, . \end{align*} 於是，系統$A$在正則系綜中具有能量$E_A$的機率將正比於$\Omega(E_A)\times\exp(-E_A/k_BT)$。

水的相變

統計力學的核心思想在於屏棄對微觀細節的精準掌控，專注在理解宏觀的觀測量。目前為止從能量、系綜到Boltzmann分佈，我們終於建立好基本架構來探究統計力學中的各種問題了！而第一個(可能也是最重要的)主題就是「相變(phase transition)」。

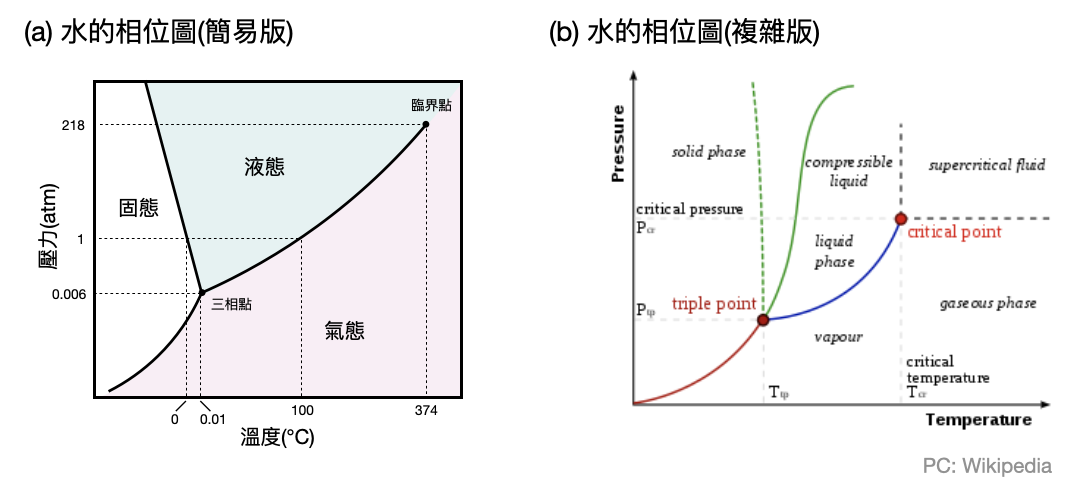
以日常生活中每天都會出現的“水”為例，在不同溫度之下，可以呈現出截然不同的三種樣貌：液態(liquid)、固態(solid)和氣態(gas)，這些宏觀狀態又被稱為水的各種相(phase)。當拿到一堆水分子時，即使無法知道詳細的微觀狀態，一般人還是能夠輕易地判斷出這堆水分子是處在哪一個相(phase)。因此，理解一堆水分子是如何在不同的相之間轉換，就成為了統計力學中最基本的問題之一。

(a)中學課本會出現的三相圖(x軸是溫度，y軸是壓力)，圖中的黑線對應到了(一級)相變，代表水的宏觀狀態會在那一瞬間突然改變。而最右邊有個點是臨界點(critical point)，代表在那邊液態和氣態已經共存且無法區分，對應到了(二級)相變。相關概念將會在介紹Ising模型後更仔細討論。(b)複雜版的相位圖。

讓我們再更進一步從日常經驗中思考水分子的相是如何變化的，在平地的大氣壓之下，當溫度很低的時候會處於固態(冰)，直到溫度超過冰點後就會轉為液態(水)，而加溫超過100度c後則會變成氣態(水蒸氣)。更重要的是，從固態到液態，以及從液態到氣態的轉換，都是在一個固定的溫度(冰點和沸點)時瞬間發生的，如此突然改變相的現象，又被稱為相變。

不過既然我們都花時間學這麼多統計力學的概念了，應該可以更深入的解釋相變以及一些相關的概念。而一切可以從統計力學中最簡單也可以說是最重要的數學模型說起：「Ising模型(Ising model)」。

Ising模型

生活中常見的鐵(Iron)或是較少聽過的鎳(Nickel)和鈷(Cobalt)，當沒有外加磁場的時候並不會展性任何磁性。一旦將一塊磁鐵靠上去之後，就會暫時被磁化(例如你家冰箱的外殼)。這樣的物理性質，被稱為「鐵磁性(Ferromanetism)」，而Ising模型就是個最經典描述鐵磁材料的抽象數學模型。但除了解釋這些具體的物理材料之外，Ising模型的重要性更在於數學上展現了豐富的物理性質，並且成為許多理論研究的起手式。

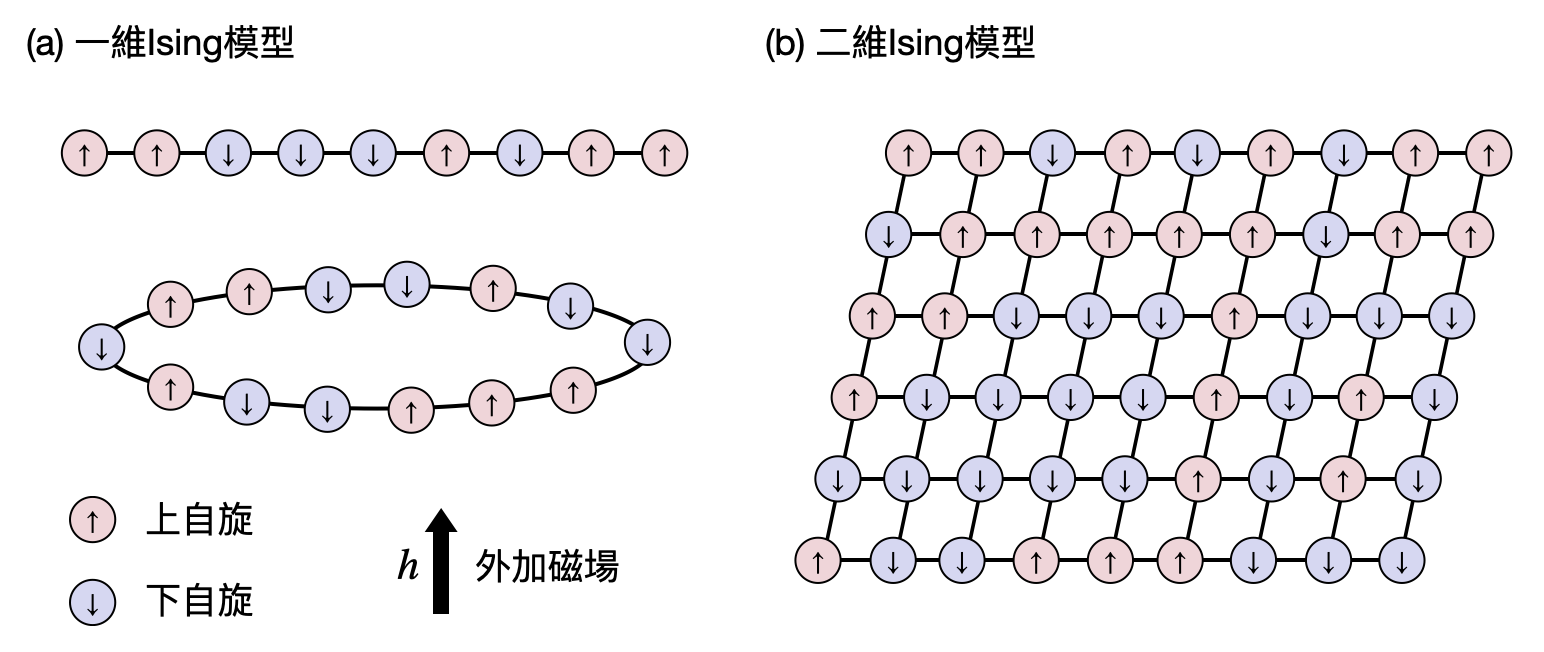
在Ising模型中，會有$N$個自旋可以為上或下的粒子，在數學上被描述為一個長度為$N$的$\{+1,-1\}^N$字串/向量，通常又會被稱為自旋態(spin state)。此外，還會有一些系統變量，定義出系統的能量(漢米爾頓量)。在最基礎的Ising模型中，一般會有兩種變量：(i)交互作用量(interaction/coupling)$J$和(ii)外加磁場(external magnetic field) $h$。一旦設定好所有粒子$i$和$j$之間的交互作用量$J_{ij}$以及每個粒子$i$的磁場$h_i$之後，整個系統的能量可以被寫成： \begin{equation*} E(\sigma) = -\sum_{i,j} J_{i,j}\sigma_i\sigma_j - \mu\sum_ih_i\sigma_i \end{equation*} 其中$\mu$是系統的磁矩(magnetic moment)，對於沒有物理背景的讀者來說，可以就把它想成是個給定的常數就好。

(a)一維Ising模型。兩種常見的變形分別是上圖的封閉性邊界(closed boundary)和中圖的週期性邊界(periodic boundary)。(b)二維Ising模型。

交互作用和外加磁場的直觀意義： 該如何理解能量函數$E$中的交互作用量$J_{ij}$和外加磁場$h_i$的含義呢？

讓我們先從比較簡單的$h_i$開始，由於系統會傾向能量低的狀態，所以當$h_i>0$時，$\sigma_i=+1$將會具有比較低的能量。反之當$h_i<0$時，$\sigma_i=-1$將會具有比較低的能量。也就是說，$h_i$的正負號會影響第$i$個自旋的方向，很符合了外加磁場的物理圖像。
至於交互作用量，當$J_{ij}>0$時，系統會傾向讓$\sigma_i$和$\sigma_j$的正負號相同。反之當$J_{ij}<0$時，系統會傾向讓$\sigma_i$和$\sigma_j$的正負號相反。因此，$J$的正負號決定了第$i$和第$j$個粒子之間是具有「鐵磁性(ferromagnetic)」還是「反鐵磁性(antiferromagnetic)」，也就是說系統是傾向讓這兩個粒子具有相同、或是相反的自旋方向。

一旦有了系統的能量函數，我們就可以直接套用前面建立的架構。對於任何的溫度$T$，任何一個自旋態$\sigma\in\{+1,-1\}^N$的機率(例如在微觀或正則系綜之下)將會是 \begin{equation*} P_{\beta}(\sigma) = \frac{e^{-E(\sigma)/kT}}{\sum_{\sigma’}e^{-E(\sigma’)/kT}} = \frac{e^{-\beta E(\sigma)}}{Z_\beta} \end{equation*} 其中$\beta=1/kT$是統計物理中慣用來替代$T$的變數，$Z_{\beta}=\sum_{\sigma’}e^{-E(\sigma’)/kT} = \sum_{\sigma’}e^{-\beta E(\sigma’)}$是系統的配分函數。

有了對微觀狀態(也就是自旋態$\sigma\in\{+1,-1\}^N$)的的機率假設之後，我們就可以計算配分函數和各種有趣的觀測量了！例如，一個常見的觀測量是「磁化程度(magnetization)」$m$，被定義為$\langle\sum_{i}\sigma_i/N\rangle$，其中$\langle\cdot\rangle$代表了用上述的Boltzmann分佈計算期望值。所以一旦能夠將配分函數$Z_\beta$寫成$J_{i,j}$、$h_i$、和$\beta$的函數，那麼就可以透過計算$Z_\beta$對$h_i$的偏微分來得到磁化程度$m$。

現在，讓我們透過以下最簡單的一維Ising模型來看看具體化以上的討論。對於數學細節沒有那麼感興趣的讀者，可以將下面出現的各個公式理解為“雖然醜陋，但是至少有個公式解”。而對自身數學能力有把握的讀者，如果還沒有計算過一維Ising模型的話，不仿試試看算一遍，看能不能抓出筆者的計算瑕疵。

考慮$n$個自旋粒子排在一條圓圈上，只有相鄰的兩個粒子會具有$J$的交互作用量，然後每個粒子的外加磁場大小為$h$，也就是

\begin{equation*} E(\sigma) = -J\sum_{i=1}^N\sigma_{i}\sigma_{i+1} - h\sum_{i=1}^N\sigma_i \end{equation*}

其中$\sigma_{N+1}=\sigma_1$。在一系列還算標準的數學計算之後，可以得到以下的配分函數 \begin{equation*} Z_\beta = \lambda_+^N + \lambda_-^N \end{equation*} 其中 \begin{equation*} {\small\lambda_{\pm} = e^{\beta J}\left[\cosh(\beta h)\pm\sqrt{\cosh^2(\beta h)-2e^{-2\beta J}\sinh(2\beta J)}\right]} \end{equation*} 以及$\cosh(a)=(e^a+e^{-a})/2$和$\sinh(a)=(e^a-e^{-a})/2$是雙曲函數。有了這個配分函數的表達式，我們就可以輕鬆地算出以下這些觀測量：

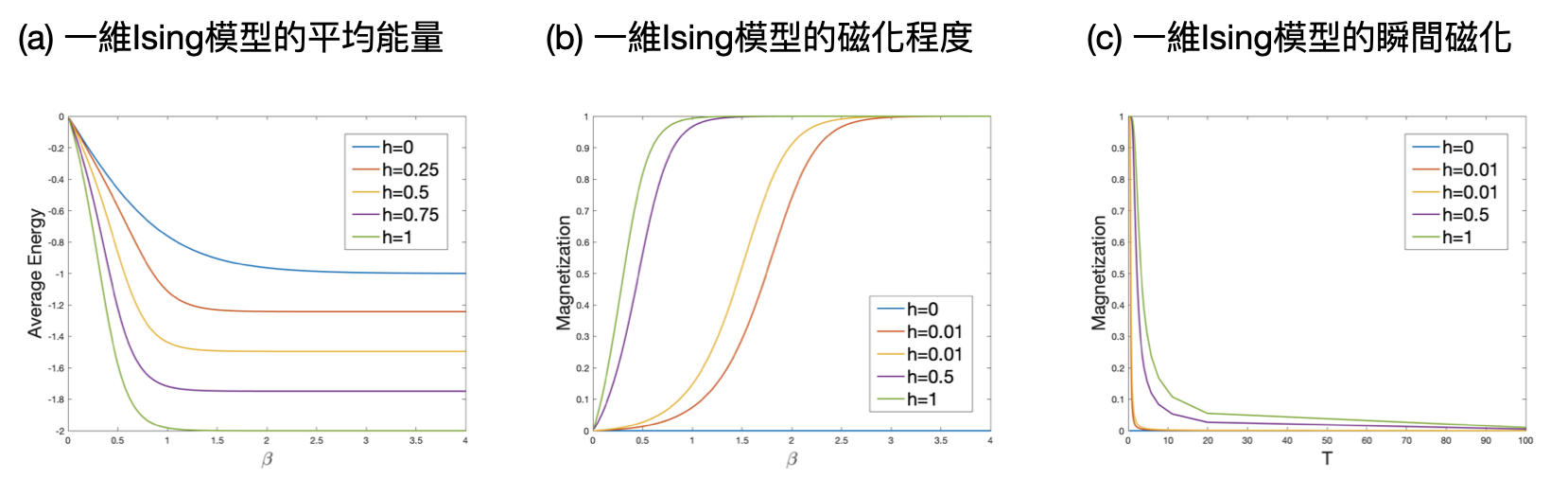
平均能量： \begin{align*} &{\small\langle E/N\rangle=-\frac{\partial \ln Z_\beta}{\partial\beta}/N}\\
{\scriptsize\approx}\ &{\scriptsize -J - \frac{e^{\beta J}}{\lambda_+}\cdot\left( h\cdot\sinh(\beta h) + \frac{h\cdot\cosh(\beta h)\sinh(\beta h)-2Je^{-4\beta J}}{\sqrt{\cosh(\beta h)^2 - 2e^{-2\beta J}\sinh(2\beta J)}} \right)} \end{align*}
磁化程度： \begin{align*} &{\small\langle \sum_i\sigma_i/N\rangle=\frac{\partial \ln Z_\beta}{\partial h}/(\beta N)}\\
{\small\approx}\ &{\scriptsize \frac{e^{\beta J}}{\lambda_+}\cdot\left(\sinh(\beta h) + \frac{\cosh(\beta h)\cdot\sinh(\beta h)}{\sqrt{\cosh(\beta h)^2 - 2e^{-2\beta J}\cdot\sinh(2\beta J)}} \right)} \end{align*}

上面這些式子乍看之下的確有點醜陋，讀者可別嚇到了，能夠有公式解總比沒有好！而寫出這些式子的主要目的，只是要讓讀者感受解一個Ising模型的意思到底是麼，除非真的很感興趣，不然沒有必要去看懂所有的推導過程。

有了公式解之後就可以直接計算並且圖像化一維Ising模型的各種性質。圖中使用J=1。(a)平均能量。(b)磁化程度。(c)當使用溫度T作為x軸，可以觀察到一維Ising模型在溫度T=0時瞬間磁化。

相變與臨界現象

從一維Ising模型的例子中，我們看到了如何從之前學到的系綜、Boltzmann分佈、配分函數等概念，將抽象的數學模型轉化為生動且量化的物理圖像。不過一維的Ising模型能展現的物理概念終究很局限，例如其“臨界現象”只能發生在溫度是零的時候。於是，一個重要的問題來了：是否能有個數學模型刻畫物理世界中在非零溫度產生的臨界現象(例如水的兩種相變都是在非零的溫度)？

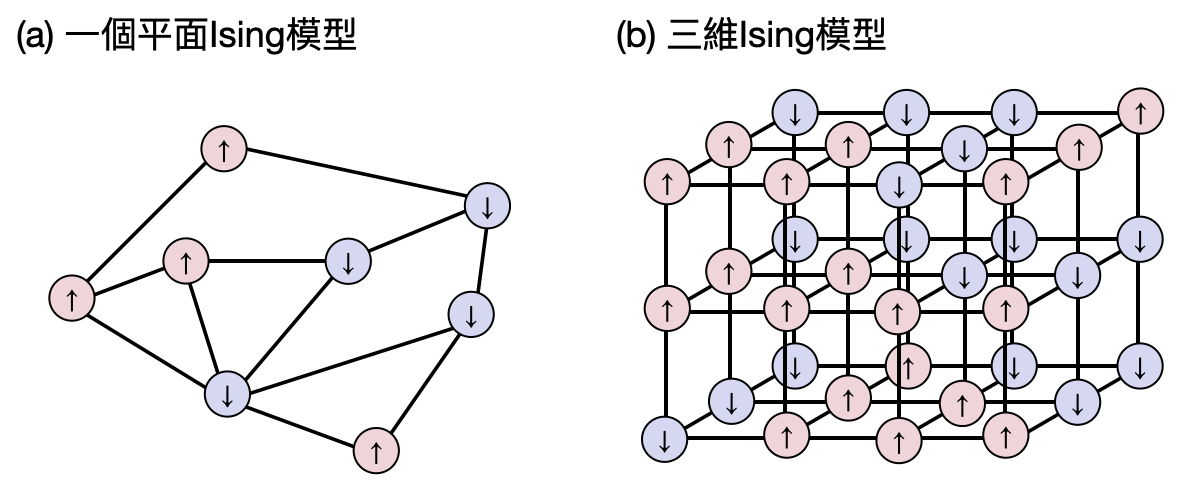
Lars Onsager是個物理與化學雙棲的挪威人，生於一戰前的1903年並在1968年獲得諾貝爾化學獎，Onsager另外一個廣為人知的重要成就，是在1944年給出了第一個(有完整數學嚴格分系的)具有在非零溫度產生臨界現象的Ising模型。他考慮的模型很簡單：二維不具有外加磁場的Ising模型(如下圖(a))。他的結果激起了許多數學家和物理學家對於Ising模型(和其他的統計力學模型)的興趣，試圖找出更多像一維和二維Ising模型一樣有完整數學解的模型。然而對於更複雜的模型例如二維具有外加磁場、三維甚至是有複雜的遠程作用力的模型，雖然我們仍然能夠寫下能量函數，但是其配分函數通常很難被寫成一個乾淨的公式，因此物理學家通常要嘛會使用電腦數值，或是透過一些猜測和數學上的省略假設來獲得近似的結果。

在這邊，為了要讓讀者以最容易又不失重點的方式學到統計物理中最核心的概念：「臨界現象(critical phenomena)」，就讓我們以二維Ising模型(具有外加磁場)為例，直接用電腦數值模擬的結果(對數學公式解感興趣的讀者請參考延伸閱讀)來闡述底下的物理直覺。

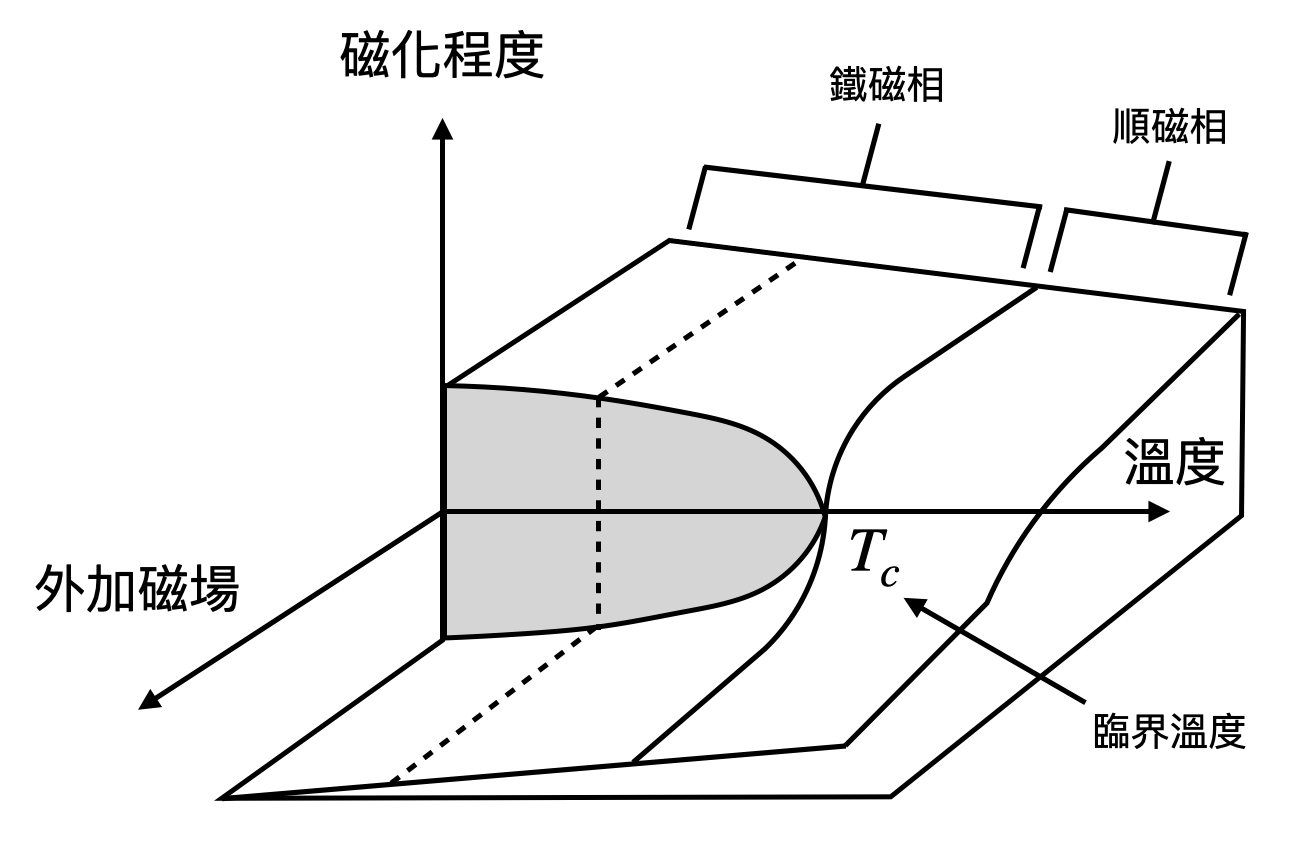
二維Ising模型的磁化程度函數。圖中三個軸分別代表溫度T(x軸)、外加磁場h(y軸)、和磁化程度m(z軸)。與一維Ising模型(參考之前的圖片)很不同的地方在於，二維Ising模型會在某個有限非零的臨界溫度(Tc)發生臨界現象。因此，當低於臨界溫度時，二維Ising模型將會發生瞬間磁化的現象，例如沿著圖中的虛線調動外加磁場的大小。

鐵磁相、順磁相與瞬間對稱性破缺： 讓我們先從沒有外加磁場的情況(也就是$h=0$)開始，這時候結果就已經和一維Ising模型很不一樣了！竟然存在一個特殊的臨界溫度(有時候又被稱為Curie溫度)$T_c>0$，一旦溫度$T<T_c$，就算沒有外加磁場二維Ising模型仍然具有非零的磁化程度！而當溫度為$T>T_c$時，如果沒有外加磁場，那麼磁化程度將會是零。

這樣的現象，讓物理學家很自然的將$T<T_c$和$T>T_c$兩個不同的溫度範圍，定義為不同的相，分別為鐵磁相(ferromagnetic phase)與順磁相(paramagnetic phase)。前者暗示著在沒有外加磁場的情況下就像個磁鐵一樣，後者則是需要有外加磁場才能順著磁場的方向產生磁性。那如果$T=T_c$呢？這就是相變發生之處，又被稱為臨界點(critical point)。現在讓我們做個思想實驗，讓我們把外加磁場固定為零($h=0$)，然後從臨界溫度$T_c$之上，慢慢將溫度$T$調低，並跨越$T_c$(如上圖的第一條粗黑線)。在這個過程中，系統的磁化程度一開始會保持為零，直到跨越$T_c$的那一刻後開始變大。更精彩的是磁化程度的方向(正負號)將會被隨機的決定，這又被稱為瞬間對稱性破缺(spontaneous symmetry breaking)。

瞬間磁化： 現在我們可以來討論外加磁場帶來的效果了！透過將磁化程度寫成溫度$T$和外加磁場$h$的函數$m(T,h)$，我們可以固定住溫度，然後討論不同強度的外加磁場帶來的效果為何(如上圖的第二條粗黑線)。

這時候有趣的現象發生了：當溫度低於臨界溫度時($T<T_c$)，磁化程度將會是不連續的！換句話說，當我們慢慢將外加磁場的大小從$h>0$慢慢地調到$h<0$時，系統的磁化程度$m(T,h)$將會突然從一個正的非零值，瞬間跳到一個負的非零值。用另外一個物理圖像來理解，如果你刻意將二維Ising模型初始在一個不具有磁場的微觀狀態，並且放置在低於臨界溫度的地方，那麼只要加一點點外加磁場，系統的磁化程度將會瞬間從零跳到一個距離零很遙遠的數值。也就是說，系統瞬間磁化(spontaneous magnetization)了！

一級相變、二級相變與有序參量： 上述在二維Ising模型的兩種相變，又分別對應到了二級相變(second order phase transition)與一級相變(first order phase transition)。後者是個離散的相變，系統在跨越相變點時會產生巨大的改變，例如水從液態變固態時就是發生了一級相變。而前者則是個連續的相變，系統的某個宏觀量在跨越相變點時發生了量性的改變。例如在二維Ising模型中，磁化程度原本一直為零，在跨越二級相變的臨界點之後才開始急遽(但是是連續的)改變。這個關鍵地刻畫二級相變在不同相位差異之處的宏觀量，又被稱為「有序參量(order parameter)」。在上述的例子中，磁化程度$m$就是個有序參量。

之前水的三相圖中那個奇怪的臨界點，也是個二級相變發生之處。由於我們生活中沒有經歷過如此高溫高壓的環境所以可能很難想像，不過從Ising模型的數學圖像說不定能反過來幫助讀者理解水的臨界點！

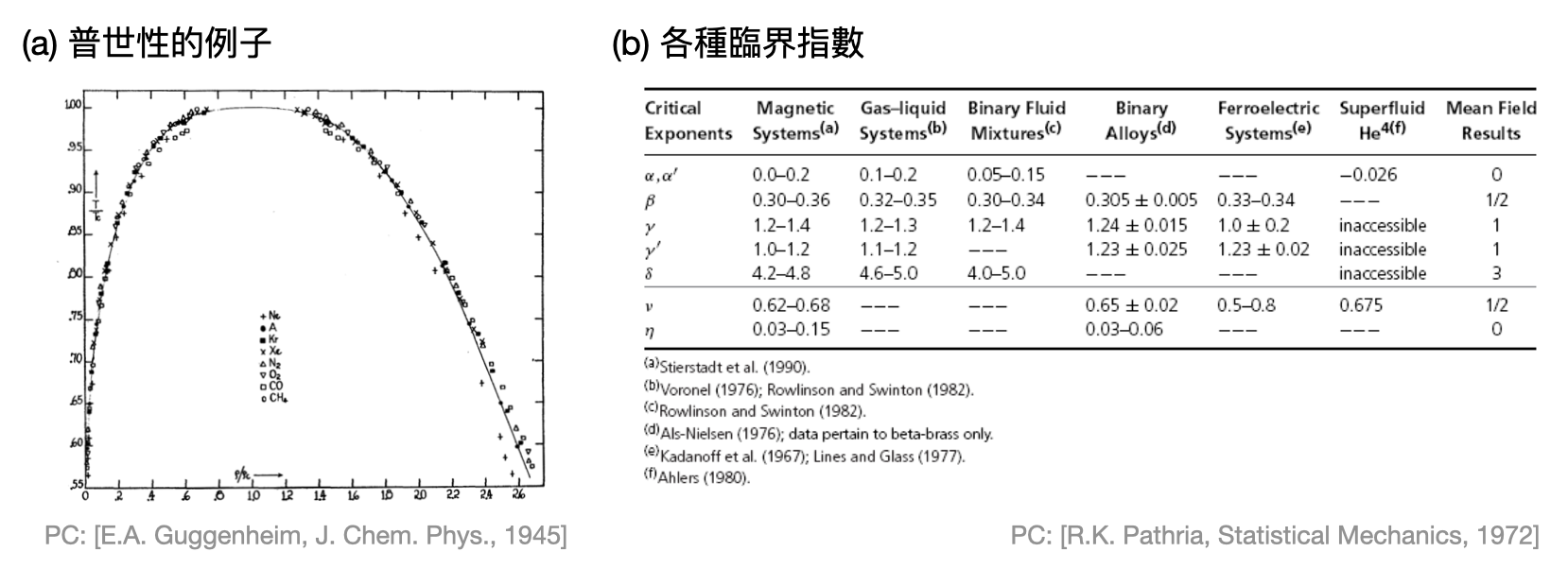
普世性與臨界指數

如果你有耐心讀到此處，心裡也許會納悶，難道每次想要研究一個物理系統的時候，都要這樣重新定義能量函數、解配分函數、計算各種觀測量找相變嗎？的確在前兩步是這樣沒錯，然而在研究相變的時候，很驚人的是，物理世界中我們感興趣的系統和現象，竟然很多時候在接近臨界點時都具有差不多的宏觀表現！這種美麗的巧合又被稱為「普世性(universality)」，而兩種物理模型/系統如果在臨界點具有類似的宏觀變化，就會被稱為處於相同的普世類別(universality class)。

(a)普世性的一個例子：八中不同分子的濃度在液態-氣態相變時，具有相同的變化速率([E.A. Guggenheim, J. Chem. Phys., 1945])。(b)各種模型的各種臨界指數([R.K. Pathria, Statistical Mechanics, 1972])。

該如何具體描述普世性呢？透過研究宏觀量(例如之前提到的有序參數)在臨界點附近的數值，我們可以計算出其值與離臨界點之間的距離呈什麼關係。以之前二維Ising模型為例，當溫度$T$低於臨界溫度$T_c$且沒有外加磁場時，磁化程度$m$的大小會正比於$(T_c-T)^\beta$，其中$\beta$是個常數(在這邊大約是1/8)，又被稱為這個系統/模型的「臨界指數(critical exponent)」。於是，物理學家將具有同樣臨界指數的系統/模型歸在同一個普世類之內。上圖(b)中展示了各式各樣常見的臨界指數。

無序與玻璃相

2021年諾貝爾物理獎的三個名額中，其中一個頒給了自旋玻璃學(spin glass)的祖師爺Giorgio Parisi。Parisi在分析自旋玻璃學中的「Sherrington–Kirkpatrick模型(SK model)」時，開創了一系列強大的數學分析工具，不但能夠給出非常精準的預測，還為許多物理現象提供了深入的圖像。

物理可以說是門研究「對稱性(symmetry)」的學科，這裡所謂的對稱性不僅僅包含生活中直覺的幾何對稱性，而是更廣義的泛指能夠保有「不變量(invariance)」的物理操作。例如，看到一顆球的時，為什麼你會覺得它很對稱呢？一個觀點是，因為不管你旋轉什麼方向，它都還是看起來沒有變。而對於一顆方塊來說，只有轉很特定的角度才會讓他看起來不變。至於一顆地上隨便撿的石頭，很高的機會將不會具有任何操作讓它看起來是一樣的。這些能夠維持一個系統的不變量的操作，又被稱為其「對稱群(symmetry group)」。一旦系統有著具有豐富數學結構的對稱群，那物理學家就很高興了，大量的數學工具將可以利用這些對稱性來剖析系統的物理性質。

然而在很多稍微複雜的物理系統中，對稱性不再容易被找到，很多時候甚至系統是沒有對稱性的，這樣的情況又被稱為「無序(disorder)」。在這樣的情況之下，該如何研究物理呢？

一個很棒的做法就是物理學家自己在模型中定義什麼是無序！在SK模型中，Sherrington和Kirkpatrick很聰明的將無序定義在粒子的交互作用量$J$上。具體來說，他們考慮一個具有$N$個粒子，兩兩都具有交互作用力的Ising模型，並且將第$i$和第$j$個粒子之間的交互作用量$J_{ij}$取為隨機的！如此一來無序被引入模型之中，讓物理學家有機會從隨機性的美好數學結構中萃取出對稱性和新發現。

不過這樣引入無序的數學方式，背後有相對應的物理圖像嗎？有的，SK模型中隨機選取交互作用量的方式，竟然對應到了製作玻璃的過程！

玻璃的主要成分是石英(二氧化矽)，在高溫時玻璃將會是處於液態，各個分子將會隨機的流動，於是分子之間因為化學鍵產生的交互作用力也會隨著相對位置的不同而隨機變化。在製作(固態的)玻璃時，標準的做法是「淬火(quenching)」：利用快速降溫使液態迅速變為固態。由於這個過程在很短的時間內完成，所以每個分子還沒來得及變動太多，就被固定住了。這代表分子間兩兩的交互作用力，也將會約略維持淬火前的大小。也就是說，SK模型在低溫(低於臨界溫度)時，對應到了玻璃經淬火後被瞬間封印的無序。這樣的「玻璃相(glassy phase)」，促使出Parisi發現了「複本對稱性破缺(replica symmetry breaking)」，並在四十年前打開了統計物理的新頁，近十幾二十年也帶給理論電腦科學許多新的視角。

統計力學與計算

在學習了這麼多熱力學和統計力學的知識後，希望讀者對於統計力學的“世界觀”有了更多的物理直覺與數學圖像。這個龐大的體系除了乘載著豐富的物理故事之外，更是不意外地和計算有著數不清的關聯。在本章剩餘的篇幅中，我們將看到五個統計力學與計算相關的面向，這必定只是兩者緊密關係間的幾個小見證而已，在未來可能還會有更多有趣的連結等著被發現。

Ising模型、最大切割問題與布爾可滿足性問題
Ising模型的可解性與計算複雜度
隨機模型與平均狀況複雜度
推論統計學
統計力學中的演算法

Ising模型、最大切割問題與布爾可滿足性問題

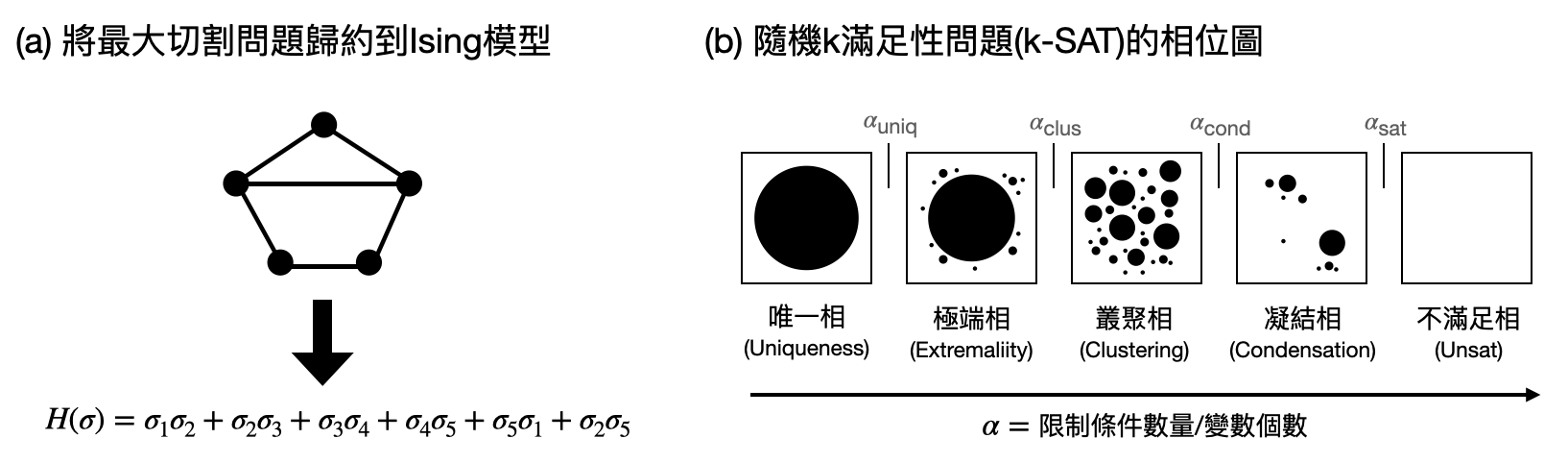
看了這麼多Ising模型的介紹，除了用來描述物理世界中各種臨界現象之外，它跟計算有什麼樣的關係呢？讓我們回顧一下之前在第二章認識的最大切割問題(Max-Cut)：給定一個圖$G$(具有一個頂點集合$V$和邊集合$E$，在符號上別和能量函數$E(\sigma)$搞混了)，找到一個將頂點分成兩堆的切割，使得越多的邊跨越切割。

現在，給定隨便一個圖$G$，並且設置一個Ising模型使得其交互作用力是根據$G$的邊來決定的。具體來說，如果點$i$和點$j$在$G$中形成一個邊，那就在Ising模型中讓$J_{ij}=1$。在物理直覺上，這就是想要鼓勵第$i$和第$j$個粒子選擇相反的自旋方向。而數學上，我們得到以下的能量函數 \begin{equation*} E(\sigma) = \sum_{(i,j)\in E}\sigma_i\sigma_j \, . \end{equation*} 仔細盯著$E(\sigma)$看，會發現這個Ising模型的基態(也就是能量最低的態)會對應到$G$中最大的切割！為什麼呢？假設$G$有$m$邊，且$\sigma$(現在想成用其+1/-1將點區分，因此是個$G$的切割)的切割大小是$k$，那麼$E(\sigma)$將會是$(m-k)-k=m-2k$，也就是當切割量越大，能量越小！

透過最大切割問題和Ising模型間如此自然的關聯，我們便可以利用統計力學的工具來分析最大切割問題了。雖然在統計力學中，物理學家不會考慮“任意”的圖$G$，但是對於某些具有物理意義的$G$，或是像SK模型對應到具有無序(隨機性)的圖，理論物理學家開發的技術就能帶來許多新的視角和結論。

而Ising模型和計算問題的關聯可不只有在最大切割問題，透過引入更廣義的作用力量，Ising模型也可以很自然的和其他之前提過的布爾可滿足性問題(Boolean satisfiability problem)產生連結：將各個限制條件寫進一個能量函數裏面。這些統計物理和理論電腦科學的交流，更是在近年激盪出許多對隨機布爾可滿足性問題中臨界現象的詳細刻畫。

(a)將最大切割問題歸約到Ising模型：把圖中每個邊都轉換成相對應兩個粒子之間的交互作用力。(b)在隨機k滿足性問題(k-SAT)中，每個限制條件會從n個布爾變數中隨機選出k個，並且隨機決定是否將其否定(negated)，然後考慮這些文字(literal)的邏輯或(logical or)。當限制條件越多，隨機k-SAT就會越來越沒有解答。而透過分析隨機k-SAT的解答空間，會發現隨著限制條件數量和變數個數的比例增加，最佳解答們(圖中黑色處)會從原本全部相互連接的狀態，到慢慢分散化群，到最後消失。對許多數學物理學家來說，找出這些相變點的具體數值是一生的志業。本圖改編自[Krzakala et al., Proc. Natl. Acad. Sci, 2007]，感興趣的讀者可以在裡面看到更多細節。

Ising模型的可解性與計算複雜度

“P vs. NP問題”困擾了理論電腦科學家與一些數學家超過半個世紀，同時，該如何將常見的統計力學模型用數學嚴謹地解開，也為難了無數聰明的理論物理學家。這兩大數學難題，竟然具有異曲同工之妙！？

先說說什麼叫做用“數學嚴謹地解開一個統計力學模型”，在術語上這又被稱為「完全可解模型(exactly solvable model)」。之前我們提到Boltzmann函數在固定一個溫度之下如何決定了系統微觀狀態的機率分佈，於是只要知道Boltzmann函數，就可以計算宏觀可測量的期望值(平均值)。在計算這些觀測量時，通常我們不需要用到整個Boltzmann函數的細節，只要能夠計算出配分函數，就能透過玩弄(取偏微分)它來算出各種可測量的期望值。例如先前提到磁化程度可以透過將配分函數對外加磁場取偏微分後得到($\frac{\partial \ln Z_\beta}{\partial h}/(\beta N)$)。於是，當我們說一個統計力學模型是可解的時候，意味著能夠將其配分函數用數學公式完整的寫下來(雖然有可能非常的巨大)。

接著來看看一些成功的例子吧！除了之前介紹的一維Ising模型(基本上是個課堂作業程度的問題)，以及Onsager解開的二維無外加磁場的二維Ising模型，後來人們又將結果推廣至所有“能夠將作用力圖畫在平面上”的Ising模型(參考下圖(a))。

(a)一個平面(planar)Ising模型的例子。(b)三維Ising模型。

然而，之後人們就再也沒有任何大的進展了，無論如何都攻破不下三維Ising模型，二維有外加磁場的Ising模型也是只能透過數值模擬研究。一直到了80年代計算複雜度開始越來越受到關注後，陸續有幾篇論文指出各種超過二維的Ising模型，以及二維有外加磁場的Ising模型，都是NP-hard的。也就是說，如果有人能夠給出其中一個模型的公式解，那就證明了P=NP。

到底三維Ising模型是否完全可解？到底NP是否被P包含住？會不會哪天有個天才不小心一次解決了這兩個問題？又或可解模型的研究終究無法逃脫計算世界的極限？

隨機模型與平均狀況複雜度

理論電腦科學是一門從「最差情況分析(worst-case analysis)」起家的學科，一個演算法必須要在所有可能的輸入上都正確才行。這樣的要求，在資訊安全或是密碼學的觀點來說很合理，畢竟我們不希望演算法有任何潛在的漏洞，更希望密碼系統可以防止任何攻擊。然而，對於一些可以稍微接受小錯誤的計算問題，或是一些我們很有把握不會出現奇怪輸入的計算場景，是否有機會可以設計出更好更快的演算法？

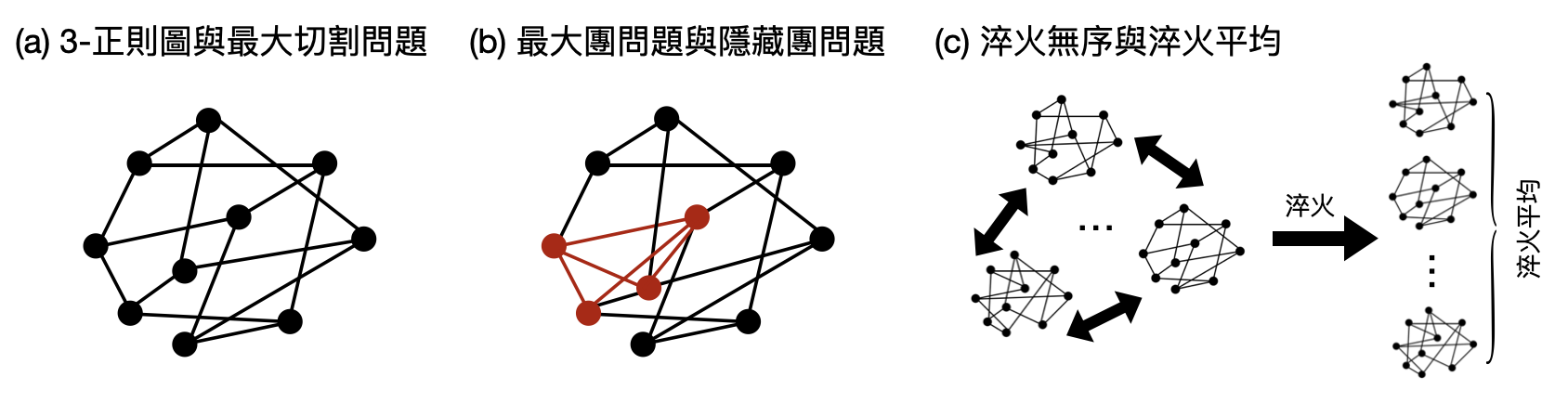
這時候，就進入了「平均狀況分析(average-case analysis)」的領地了。根據對於現實世界的認識和動機，人們設計和考慮各種不同的模型作為計算問題的輸入。例如研究最大切割問題時，考慮隨機的正則圖(regular graph)，如下圖(a)。或是研究最大團問題(maximum clqiue problem)時，考慮隱藏團問題(planted clique problem)，如下圖(b)。

(a)正則圖指的是圖中每個點具有的邊個數都是一樣的。3-正則圖指的是每個點都具有恰好三條邊。最大切割問題的一種平均狀況版本可以是考慮輸入為隨機的3-正則圖，同樣的也可以考慮4-正則圖或是5-正則圖等等。(b)隱藏團問題是另外一個常見的平均狀況複雜度計算問題，問題需要分辨兩種狀況：第一種狀況會先隨機選擇一部份的點，並且將兩兩連上邊，接著再隨機決定剩餘的邊(如圖中所示)；第二種情況則是直接隨機地決定每兩個點之間是否有邊。(c)在隨機模型中，模型的部分參數是隨機決定的(例如SK模型中的交互作用力或是隱藏團問題中哪些點先被相互連接。這些隨機性又被稱為淬火無序，對應到了當溫度高時對於輸入為何的不確定性。淬火平均則是指將觀測量根據淬火相對應的機率分佈做平均。

在考慮這些隨機模型時，通常都會有“結構(structure)”和“隨機性(randomness)”，這正恰恰落入了統計力學的範疇：當一個平均情況模型隨機產生出一個問題輸入時(例如一個隨機的正則圖)，就像是在一個統計力學隨機模型中固定住淬火無序(quenched disorder)，也就是將隨機變動的交互作用量，在瞬間降溫後凝固住了。於是，研究某個演算法在一個平均情況模型的表現好壞，可以被翻譯為研究在一個統計力學隨機模型中，某個觀測量(對應到演算法的表現)的淬火平均(quenched average)。

推論統計學

當一早出門看到地上是濕的時候，到底是半夜下了雨，還是單純有灑水車經過？如果抬頭一看是晴空萬里，大概會覺得多半是灑水車。然而如果是烏雲密佈，那可能就會覺得是下雨造成的。會有這樣直覺性的判斷，是因為從過往的經驗中，烏雲和下雨具有更強的關聯性。如此透過觀測到的部分資料對其他未知數做出推論，正是推論統計學(statistical inference)研究的主要課題。

雖然名字裡面都有統計，但這到底跟統計力學有什麼關係呢？先讓我們試著把上述的例子用一個常見的數學模型來描述：「Bayesian網路(Bayesian networks)」。

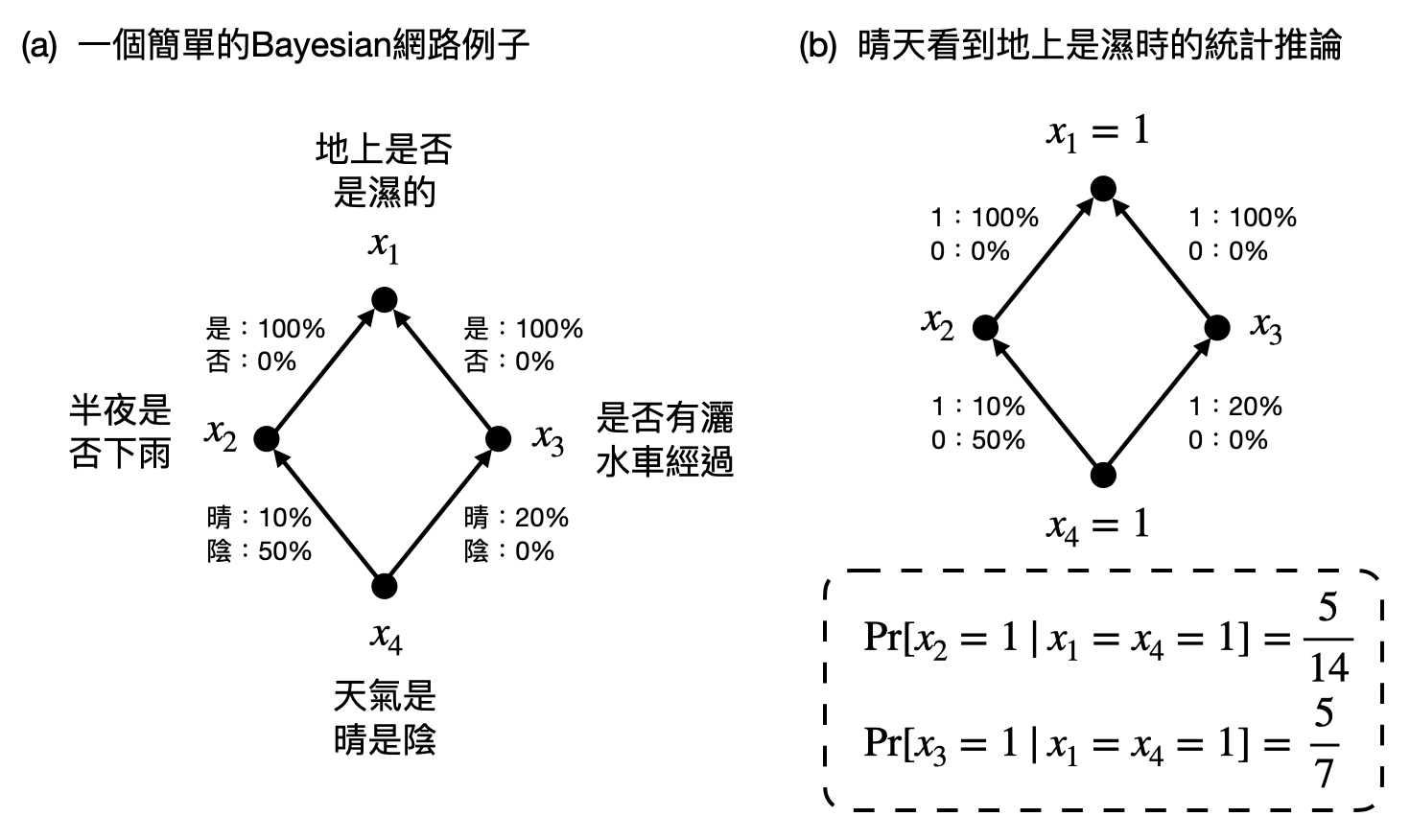
在這個例子中，有四個Boolean變數：(1)地上使否是濕的、(2)半夜是否下雨、(3)是否有灑水車經過和(4)天氣是晴是陰，這四個變數($x_1,x_2,x_3,x_4$)將具有下圖(a)的因果關係。更進一步，每條因果關係箭頭，將會具有不一樣的“強度”。例如當陰天時，可能代表有50%的機率會下雨，然而晴天時只會有10%的機率有下雨，另外有20%的機率會有灑水車經過。

(a)上述關於地上溼的原因為何的例子可以被一個Bayesian網路描述。(b)當Bayesian網路中某些數值被固定住時(例如在觀測到地上是濕的且天氣是晴的)，可以透過Bayes規則算出條件機率，作為相對應的統計推論。你能檢驗圖中的算出來的條件機率是否正確嗎？

在一個Bayesian網路中會有許多變數(variables)以及變數間的條件機率(conditional probability)，來描述具有許多因果關係的場景。如此一來，只要根據實際觀測到的數據固定住某些變數的數值後(例如在上面的例子看到地上是濕的以及天氣的陰晴就可以固定住$x_1$和$x_4$)，就可以使用Bayes規則(Bayes rule)，產生出相對應的後驗機率分佈(posterior probability distribution)。而這個分佈的在某個剩餘變數的期望值(例如$x_2$)，就將會成為我們對這個變數結果的統計推論(例如是因為下雨造成地板濕的機會)。請參考上圖(b)。

Bayesian網路很自然地就和統計力學扯上邊了：網路中的變數對應到模型中的變數，網路中的條件機率對應到模型中的交互作用力量，最終對某個變數的統計推論則對應到一個宏觀可測量！於是，統計力學用來計算宏觀觀測量數值的技術，就可以被拿來計算推論統計學模型中(除了Bayesian網路還有很多例子，像是人工神經網路(artificial neural networks))的推論值、信心指數等等。

統計力學中的演算法

在看到了這麼多統計力學和各個與計算相關領域的關聯，也許會納悶這樣的連結到底能夠帶來什麼樣的實質幫助？

首先，從統計力學到平均狀況複雜度和推論統計學，裡面考慮的數學模型和對應的計算問題基本上都是NP-hard或是#P-hard(#P是個比NP還要更難的複雜度類別)的。也就是說，理論電腦科學家不太會期待可以有什麼演算法能夠快速的處理這些問題。

然而，對(大多數的)物理學家來說，跟數學上的嚴格性比起來，他們更在意的是能否對問題有任何進展。因此，許多乍看之下會失敗且沒有太多數學保證的務實型演算法(又被稱為啟發式演算法, heuristic algorithm)就被廣泛的使用在理論分析與數值實驗中。一些常見的務實型演算法甚至在後來漸漸被嚴格地證明在某些情況下是正確的。

在本章剩下的篇幅中，我們將看看幾個統計力學中最被廣泛使用和討論的務實型演算法。

模擬退火演算法(Simulated annealing)： 在冶金或製作玻璃時，首先會需要將材料加熱到很高溫，才能方便塑形，接著再將溫度調回室溫，拿到可以使用的產品。然而，在高溫時，材料除了開始有流動性之外，也會吸收多餘的熱能，並被粒子們以應變能(strain energy)等形式儲存著。這些多餘的能量如果沒有被適當排出，當材料回到低溫時，就很容易因為一些微小的擾動導致這些能量被瞬間釋出，造成材料的破損。

於是，在冶金工業中很重要的一個步驟就是「退火(annealing)」，概念上就是希望透過比較有計劃地將高溫的材料慢慢降溫(也就是退火)，適當地在過程中釋出多餘的能量，使得最後的產品能夠比較不易碎和耐用。

透過統計物理和優化計算問題的糾纏關係，退火這樣一個物理/化工的概念，竟然可以對應到一類的演算法：「模擬退火演算法(simulated annealing)」！

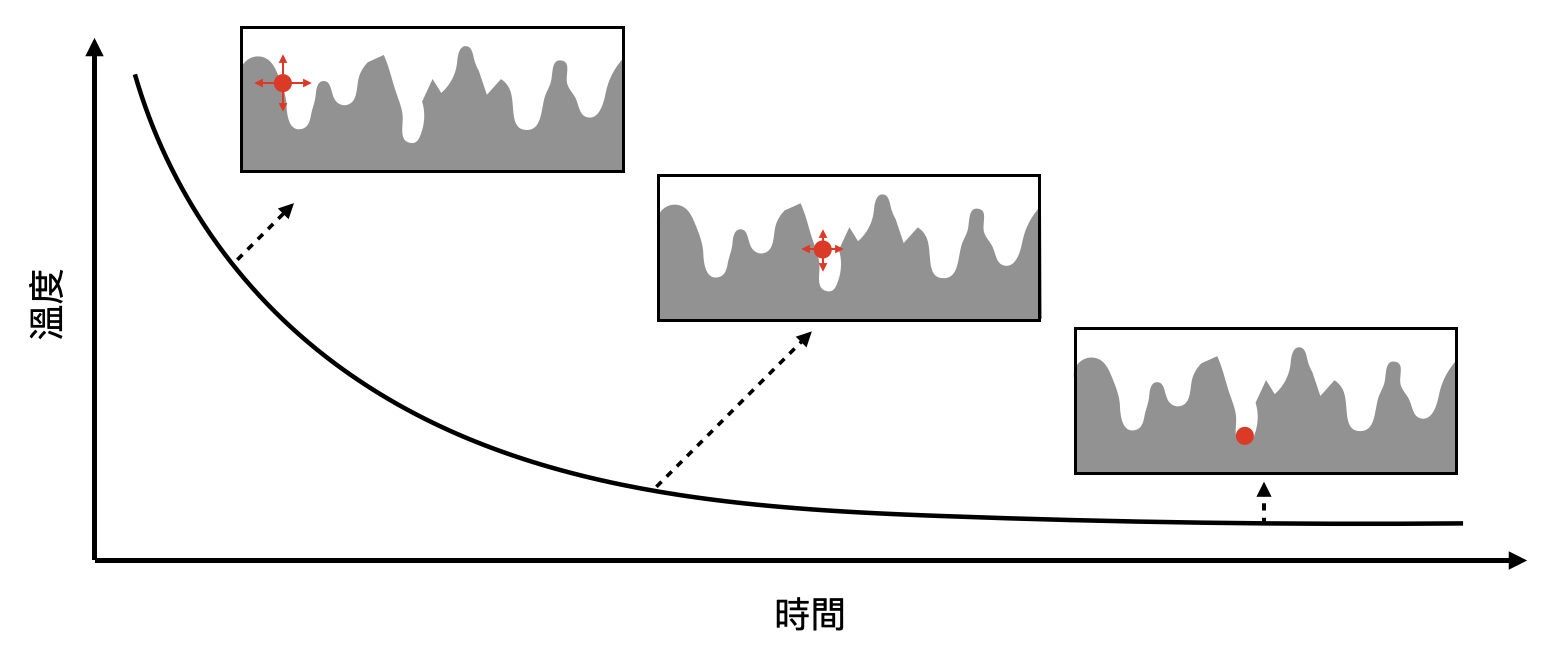
當我們想要計算一個給定的能量函數$E(\sigma)$的基態(或換句話說找到讓能量函數最小的解答)時，可以先從一個隨機的狀態開始，對應到了系統很高溫時，每個微觀狀態都具有差不多的出現機率。接著，我們可以慢慢的調低溫度參數$T$(或等價於調高$\beta$參數)，然後利用相對應的Boltzmann分佈來採樣上一個狀態附近的狀態，這對應到了退火時系統微觀狀態的改變，會比較傾向能量低的狀態。如此不斷重複降溫、採樣，最後得到一個狀態作為基態的一個近似。

模擬退火演算法在操作上就是個調控溫度的過程。當溫度高時，系統處於較興奮的狀態，於是可以在能量地貌(energy landscape, 也就是在系統狀態空間中再多加一個軸向來表示每個狀態的能量大小)上大步行走，有較高機率跳出局部最小值(local minimum)，進而探索全局最小值(global minimum)。當溫度低時，系統已經退火，所以不會再有太大的改變，只會在所處的附近走到局部能量最小的地方。

實際在使用模擬退火演算法時，人們會根據對能量函數的理解和假設，設計退火的速度、採樣的方式等等，而由於大部分的優化問題基本上都是NP-hard的，於是我們並不會期待模擬退火演算法真的會幫我們找到基態。由於模擬退火演算法非常容易實現，而且有很多設計的空間，所以在實務上通常都只是利用它來找到基態還不錯的一個近似，在理論上很難有很乾淨的數學保證。

信念傳播演算法與近似信息傳遞演算法： 還記得之前在推論統計學相關段落提到的Bayesian網路嗎(建議讀者可以往回翻去看一下附圖)？Bayesian網路讓人可以很方面地描述不同事件之間的因果/機率關係，不過其實Bayesian網路只是「因子圖(factor graph)」的一個子類別而已，更多常見的應用可以輕鬆地用因子圖來描述。

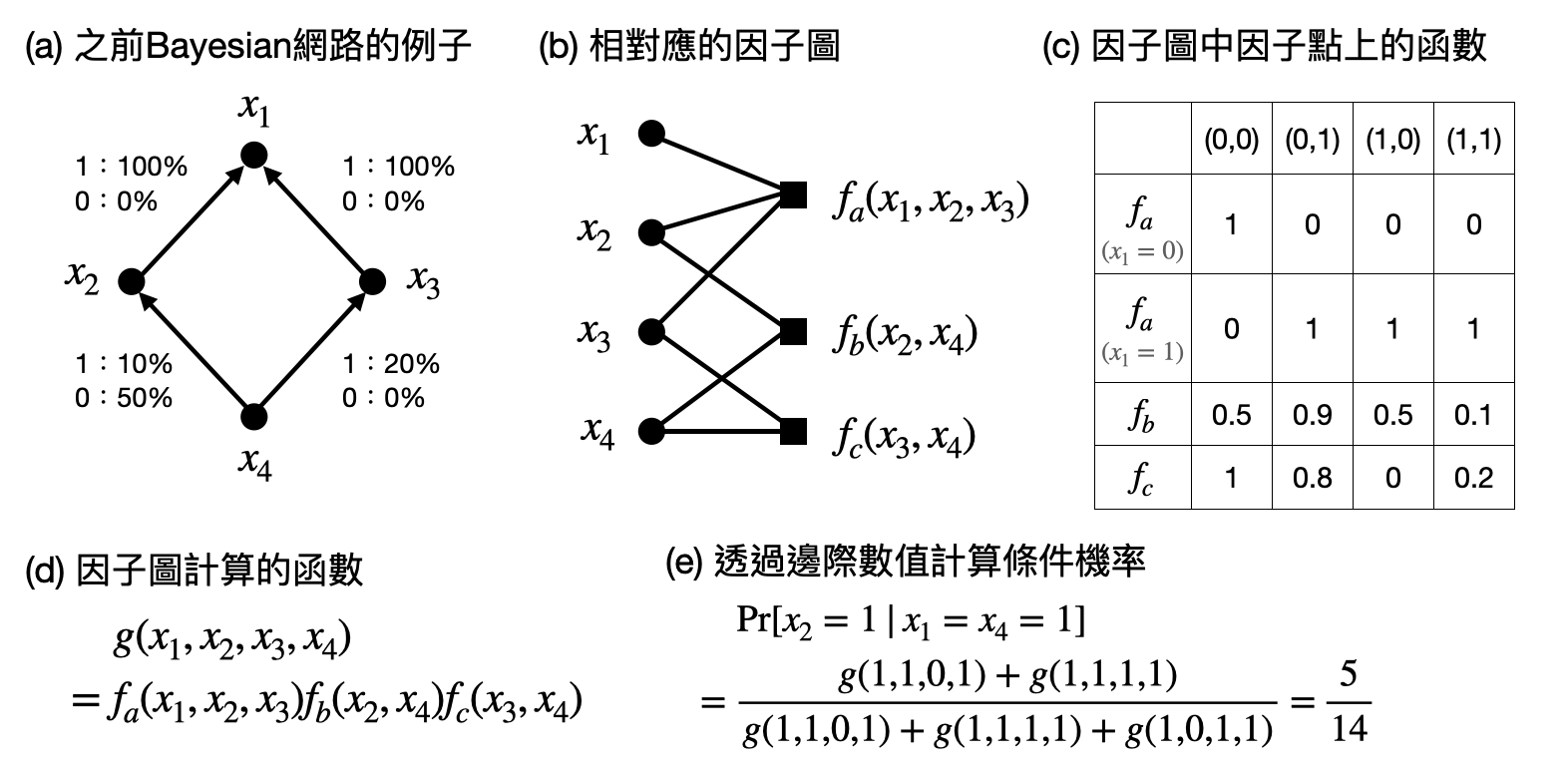
在因子圖中，有兩種類型的節點：變數點(variable vertices)和因子點(factor vertices)，而邊只能處在兩種不同的點之間。因此，因子圖是個二分圖(bipartite graph)。每個因子點會對應到一個函數，可以作用在相鄰地變數點上面。而整個因子圖對應到的函數，就是將所有因子點上的函數相乘起來，這個整體的函數就像是對應到了統計力學模型中的Boltzmann/Gibbs分佈。第一次接觸到因子圖的讀者現在也許已經暈頭轉向了，請參考下圖的例子。

有了因子圖的概念後，再回去看看統計推論的例子時，心中的圖像就會更清晰了：以Bayesian網路為例，計算某個變數的條件機率(例如當地上是濕的和晴天時，前一晚有下雨的機率是多少)就等價於將因子圖中某些變數點的值固定(將$x_1$和$x_4$設為1)，然後計算剩餘變數點的條件期望值，這又被稱為邊際數值(marginal value)。就上述的例子來說，需要計算的邊際數值為$x_2$的$g(1,0,1,1)+g(1,1,1,1)$和$x_3$的$g(1,1,0,1)+g(1,1,1,1)$。

(a)之前在推論統計學相關段落的例子。(b)可以將圖(a)中的例子用因子圖來表示。(c)因子點上的函數。(d)整體計算的函數就是將每個因子點上的函數乘起來。(e)條件機率將可以透過計算邊際數值後獲得。

於是，我們又回到計算的領域了！現在的計算問題很明確：給定一個因子圖，再另外給定一些固定的變數值，請計算出某個尚未被固定的變數之邊際數值。

沒有很意外的，這個計算問題基本上是NP-hard的，所以我們不太可能期待有個通用的快速演算法。然而有鑒於這個計算問題在大量應用場合中出現，對於想要跑模擬看到實際結果的人來說，才不管什麼NP-hard和P是否等於NP呢！於是在這樣的背景之下，眾多務實型演算法就被開發出來了。而之中最出名的就是信念傳播演算法(Belief propagation)與近似信息傳遞演算法(Approximate message passing)。

要把這兩個務實型演算法解釋清楚，需要再花上個五到十頁跑不掉，而且大量的數學符號將會很容易讓人迷失其中。因此，請感興趣的讀者參考延伸閱讀，在這邊將只會約略的講述一下信念傳播演算法和統計物理中其他概念之間的有趣故事。

信念傳播演算法大方向的概念其實很直覺：每個(尚未賦值的)變數點先隨機設定其邊際數值，接著將這些資訊傳給相鄰的所有因子點。每個因子點搜集了各個鄰近變數點的資訊後，稍作整理後再發送新的訊息給變數點。每個變數點再根據相鄰因子點回傳的訊息更新其對自身邊際數值的“信念(belief)”。如此反覆重複，直到每個變數點對自身邊際數值的信念都收斂不再更動。

當因子圖中沒有迴圈的時候，由於訊息傳遞方向單一不會混淆(當然這還是需要使用數學遞迴證明)，所以信念傳播演算法將可以輕鬆地算出完全正確的邊際數值。有趣的是，物理學家發現在一些具有迴圈的因子圖上，雖然乍看之下信念傳播演算法應該不會表現得很好，實際上卻能夠算出完全正確的邊際數值。在深入探究之後，學者發現信念傳播演算法算出來的值，竟然會和另一個物理中的近似計算方法「Bethe近似(Bethe approximation)」一致。而Bethe近似的想法是將配分函數中原本十分複雜的熵項，用稍微化簡的公式來近似，以便直接求解。如此一來，信念傳播演算法和Bethe近似又展現了一個“動態和靜態計算互相對偶”的例子！

總結

在本章中，我們看到了統計力學如何在放棄追蹤所有細節變化之後，仍另闢新地，開發出一套由Boltzmann分佈(或有些人喜歡稱之為Gibbs分佈)領軍的強大世界觀。統計力學中的模型(例如Ising模型)不但刻畫了豐富的物理現象，更是和計算複雜度理論有著糾纏不清的關係。希望本章能夠作為讀者們再更進一步深入探究前的引路人，統計力學與計算的奧妙仍是個正在進行的旅程。