$ \newcommand{\undefined}{} \newcommand{\hfill}{} \newcommand{\qedhere}{\square} \newcommand{\qed}{\square} \newcommand{\ensuremath}[1]{#1} \newcommand{\bit}{\{0,1\}} \newcommand{\Bit}{\{-1,1\}} \newcommand{\Stab}{\mathbf{Stab}} \newcommand{\NS}{\mathbf{NS}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bh}{\mathbf{h}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\Var}{\mathbf{Var}} \newcommand{\dist}{\text{dist}} \newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\sA}{\mathscr A} \newcommand{\sB}{\mathscr B} \newcommand{\sC}{\mathscr C} \newcommand{\sD}{\mathscr D} \newcommand{\sE}{\mathscr E} \newcommand{\sF}{\mathscr F} \newcommand{\sG}{\mathscr G} \newcommand{\sH}{\mathscr H} \newcommand{\sI}{\mathscr I} \newcommand{\sJ}{\mathscr J} \newcommand{\sK}{\mathscr K} \newcommand{\sL}{\mathscr L} \newcommand{\sM}{\mathscr M} \newcommand{\sN}{\mathscr N} \newcommand{\sO}{\mathscr O} \newcommand{\sP}{\mathscr P} \newcommand{\sQ}{\mathscr Q} \newcommand{\sR}{\mathscr R} \newcommand{\sS}{\mathscr S} \newcommand{\sT}{\mathscr T} \newcommand{\sU}{\mathscr U} \newcommand{\sV}{\mathscr V} \newcommand{\sW}{\mathscr W} \newcommand{\sX}{\mathscr X} \newcommand{\sY}{\mathscr Y} \newcommand{\sZ}{\mathscr Z} \newcommand{\sfA}{\mathsf A} \newcommand{\sfB}{\mathsf B} \newcommand{\sfC}{\mathsf C} \newcommand{\sfD}{\mathsf D} \newcommand{\sfE}{\mathsf E} \newcommand{\sfF}{\mathsf F} \newcommand{\sfG}{\mathsf G} \newcommand{\sfH}{\mathsf H} \newcommand{\sfI}{\mathsf I} \newcommand{\sfJ}{\mathsf J} \newcommand{\sfK}{\mathsf K} \newcommand{\sfL}{\mathsf L} \newcommand{\sfM}{\mathsf M} \newcommand{\sfN}{\mathsf N} \newcommand{\sfO}{\mathsf O} \newcommand{\sfP}{\mathsf P} \newcommand{\sfQ}{\mathsf Q} \newcommand{\sfR}{\mathsf R} \newcommand{\sfS}{\mathsf S} \newcommand{\sfT}{\mathsf T} \newcommand{\sfU}{\mathsf U} \newcommand{\sfV}{\mathsf V} \newcommand{\sfW}{\mathsf W} \newcommand{\sfX}{\mathsf X} \newcommand{\sfY}{\mathsf Y} \newcommand{\sfZ}{\mathsf Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\bfA}{\mathbf A} \newcommand{\bfB}{\mathbf B} \newcommand{\bfC}{\mathbf C} \newcommand{\bfD}{\mathbf D} \newcommand{\bfE}{\mathbf E} \newcommand{\bfF}{\mathbf F} \newcommand{\bfG}{\mathbf G} \newcommand{\bfH}{\mathbf H} \newcommand{\bfI}{\mathbf I} \newcommand{\bfJ}{\mathbf J} \newcommand{\bfK}{\mathbf K} \newcommand{\bfL}{\mathbf L} \newcommand{\bfM}{\mathbf M} \newcommand{\bfN}{\mathbf N} \newcommand{\bfO}{\mathbf O} \newcommand{\bfP}{\mathbf P} \newcommand{\bfQ}{\mathbf Q} \newcommand{\bfR}{\mathbf R} \newcommand{\bfS}{\mathbf S} \newcommand{\bfT}{\mathbf T} \newcommand{\bfU}{\mathbf U} \newcommand{\bfV}{\mathbf V} \newcommand{\bfW}{\mathbf W} \newcommand{\bfX}{\mathbf X} \newcommand{\bfY}{\mathbf Y} \newcommand{\bfZ}{\mathbf Z} \newcommand{\rmA}{\mathrm A} \newcommand{\rmB}{\mathrm B} \newcommand{\rmC}{\mathrm C} \newcommand{\rmD}{\mathrm D} \newcommand{\rmE}{\mathrm E} \newcommand{\rmF}{\mathrm F} \newcommand{\rmG}{\mathrm G} \newcommand{\rmH}{\mathrm H} \newcommand{\rmI}{\mathrm I} \newcommand{\rmJ}{\mathrm J} \newcommand{\rmK}{\mathrm K} \newcommand{\rmL}{\mathrm L} \newcommand{\rmM}{\mathrm M} \newcommand{\rmN}{\mathrm N} \newcommand{\rmO}{\mathrm O} \newcommand{\rmP}{\mathrm P} \newcommand{\rmQ}{\mathrm Q} \newcommand{\rmR}{\mathrm R} \newcommand{\rmS}{\mathrm S} \newcommand{\rmT}{\mathrm T} \newcommand{\rmU}{\mathrm U} \newcommand{\rmV}{\mathrm V} \newcommand{\rmW}{\mathrm W} \newcommand{\rmX}{\mathrm X} \newcommand{\rmY}{\mathrm Y} \newcommand{\rmZ}{\mathrm Z} \newcommand{\bb}{\mathbf{b}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\ket}[1]{| #1 \rangle} \newcommand{\bra}[1]{\langle #1 |} \newcommand{\braket}[2]{\langle #1 | #2 \rangle} \newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |} \newcommand{\e}{\varepsilon} \newcommand{\eps}{\varepsilon} \newcommand{\from}{\colon} \newcommand{\super}[2]{#1^{(#2)}} \newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}} \newcommand{\tensor}{\otimes} \newcommand{\eset}{\emptyset} \newcommand{\sse}{\subseteq} \newcommand{\sst}{\substack} \newcommand{\ot}{\otimes} \newcommand{\Esst}[1]{\bbE_{\substack{#1}}} \newcommand{\vbig}{\vphantom{\bigoplus}} \newcommand{\seteq}{\mathrel{\mathop:}=} \newcommand{\defeq}{\stackrel{\mathrm{def}}=} \newcommand{\Mid}{\mathrel{}\middle|\mathrel{}} \newcommand{\Ind}{\mathbf 1} \newcommand{\bits}{\{0,1\}} \newcommand{\sbits}{\{\pm 1\}} \newcommand{\R}{\mathbb R} \newcommand{\Rnn}{\R_{\ge 0}} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\C}{\mathbb C} \newcommand{\A}{\mathbb A} \newcommand{\Real}{\mathbb R} \newcommand{\mper}{\,.} \newcommand{\mcom}{\,,} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\cone}{cone} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\val}{val} \DeclareMathOperator{\opt}{opt} \DeclareMathOperator{\Opt}{Opt} \DeclareMathOperator{\Val}{Val} \DeclareMathOperator{\LP}{LP} \DeclareMathOperator{\SDP}{SDP} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\qpoly}{qpoly} \DeclareMathOperator{\qqpoly}{qqpoly} \DeclareMathOperator{\conv}{conv} \DeclareMathOperator{\Conv}{Conv} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\mspan}{span} \DeclareMathOperator{\mrank}{rank} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Span}{Span} \DeclareMathOperator{\Cone}{Cone} \DeclareMathOperator{\junta}{junta} \DeclareMathOperator{\NSS}{NSS} \DeclareMathOperator{\SA}{SA} \DeclareMathOperator{\SOS}{SOS} \DeclareMathOperator{\Stab}{\mathbf Stab} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\cE}{\mathcal{E}} \newcommand{\E}{\mathbb{E}} \newcommand{\pE}{\tilde{\mathbb{E}}} \newcommand{\N}{\mathbb{N}} \renewcommand{\P}{\mathcal{P}} \notag $
$ \newcommand{\sleq}{\ensuremath{\preceq}} \newcommand{\sgeq}{\ensuremath{\succeq}} \newcommand{\diag}{\ensuremath{\mathrm{diag}}} \newcommand{\support}{\ensuremath{\mathrm{support}}} \newcommand{\zo}{\ensuremath{\{0,1\}}} \newcommand{\pmo}{\ensuremath{\{\pm 1\}}} \newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}} \newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}} \newcommand{\rank}{\ensuremath{\mathrm{rank}}} \newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}} \newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}} \newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}} \newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}} \newcommand{\eqdef}{\ensuremath{ =^{def}}} \newcommand{\threshold}{\ensuremath{\mathrm{threshold}}} \newcommand{\vbls}{\ensuremath{\mathrm{vbls}}} \newcommand{\cons}{\ensuremath{\mathrm{cons}}} \newcommand{\edges}{\ensuremath{\mathrm{edges}}} \newcommand{\cl}{\ensuremath{\mathrm{cl}}} \newcommand{\xor}{\ensuremath{\oplus}} \newcommand{\1}{\ensuremath{\mathrm{1}}} \notag $
$ \newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag $
$ \newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}} \newcommand{\R} % real numbers \newcommand{\N}} % natural numbers \newcommand{\Z} % integers \newcommand{\F} % a field \newcommand{\Q} % the rationals \newcommand{\C}{\mathbb{C}} % the complexes \newcommand{\poly}} \newcommand{\polylog}} \newcommand{\loglog}}} \newcommand{\zo}{\{0,1\}} \newcommand{\suchthat} \newcommand{\pr}[1]{\Pr\left[#1\right]} \newcommand{\deffont}{\em} \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}} \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance \newcommand{\xor}{\oplus} \newcommand{\GF}{\mathrm{GF}} \newcommand{\eps}{\varepsilon} \notag $
$ \newcommand{\class}[1]{\mathbf{#1}} \newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements \newcommand{\BPP}{\class{BPP}} \newcommand{\NP}{\class{NP}} \newcommand{\RP}{\class{RP}} \newcommand{\coRP}{\coclass{RP}} \newcommand{\ZPP}{\class{ZPP}} \newcommand{\BQP}{\class{BQP}} \newcommand{\FP}{\class{FP}} \newcommand{\QP}{\class{QuasiP}} \newcommand{\VF}{\class{VF}} \newcommand{\VBP}{\class{VBP}} \newcommand{\VP}{\class{VP}} \newcommand{\VNP}{\class{VNP}} \newcommand{\RNC}{\class{RNC}} \newcommand{\RL}{\class{RL}} \newcommand{\BPL}{\class{BPL}} \newcommand{\coRL}{\coclass{RL}} \newcommand{\IP}{\class{IP}} \newcommand{\AM}{\class{AM}} \newcommand{\MA}{\class{MA}} \newcommand{\QMA}{\class{QMA}} \newcommand{\SBP}{\class{SBP}} \newcommand{\coAM}{\class{coAM}} \newcommand{\coMA}{\class{coMA}} \renewcommand{\P}{\class{P}} \newcommand\prBPP{\class{prBPP}} \newcommand\prRP{\class{prRP}} \newcommand\prP{\class{prP}} \newcommand{\Ppoly}{\class{P/poly}} \newcommand{\NPpoly}{\class{NP/poly}} \newcommand{\coNPpoly}{\class{coNP/poly}} \newcommand{\DTIME}{\class{DTIME}} \newcommand{\TIME}{\class{TIME}} \newcommand{\SIZE}{\class{SIZE}} \newcommand{\SPACE}{\class{SPACE}} \newcommand{\ETIME}{\class{E}} \newcommand{\BPTIME}{\class{BPTIME}} \newcommand{\RPTIME}{\class{RPTIME}} \newcommand{\ZPTIME}{\class{ZPTIME}} \newcommand{\EXP}{\class{EXP}} \newcommand{\ZPEXP}{\class{ZPEXP}} \newcommand{\RPEXP}{\class{RPEXP}} \newcommand{\BPEXP}{\class{BPEXP}} \newcommand{\SUBEXP}{\class{SUBEXP}} \newcommand{\NTIME}{\class{NTIME}} \newcommand{\NL}{\class{NL}} \renewcommand{\L}{\class{L}} \newcommand{\NQP}{\class{NQP}} \newcommand{\NEXP}{\class{NEXP}} \newcommand{\coNEXP}{\coclass{NEXP}} \newcommand{\NPSPACE}{\class{NPSPACE}} \newcommand{\PSPACE}{\class{PSPACE}} \newcommand{\NSPACE}{\class{NSPACE}} \newcommand{\coNSPACE}{\coclass{NSPACE}} \newcommand{\coL}{\coclass{L}} \newcommand{\coP}{\coclass{P}} \newcommand{\coNP}{\coclass{NP}} \newcommand{\coNL}{\coclass{NL}} \newcommand{\coNPSPACE}{\coclass{NPSPACE}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\LINSPACE}{\class{LINSPACE}} \newcommand{\qP}{\class{\tilde{P}}} \newcommand{\PH}{\class{PH}} \newcommand{\EXPSPACE}{\class{EXPSPACE}} \newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}} \newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}} \newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}} \newcommand{\PiP}[1]{\class{\Pi_{#1}P}} \newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}} \newcommand{\ATIME}{\class{ATIME}} \newcommand{\ASPACE}{\class{ASPACE}} \newcommand{\AP}{\class{AP}} \newcommand{\AL}{\class{AL}} \newcommand{\APSPACE}{\class{APSPACE}} \newcommand{\VNC}[1]{\class{VNC^{#1}}} \newcommand{\NC}[1]{\class{NC^{#1}}} \newcommand{\AC}[1]{\class{AC^{#1}}} \newcommand{\ACC}[1]{\class{ACC^{#1}}} \newcommand{\TC}[1]{\class{TC^{#1}}} \newcommand{\ShP}{\class{\# P}} \newcommand{\PaP}{\class{\oplus P}} \newcommand{\PCP}{\class{PCP}} \newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}} \newcommand{\MIP}{\class{MIP}} $
$ \newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\SAT}{\textprob{SAT}} \newcommand{\TSAT}{\textprob{3SAT}} \newcommand{\USAT}{\textprob{USAT}} \newcommand{\UNSAT}{\textprob{UNSAT}} \newcommand{\QPSAT}{\textprob{QPSAT}} \newcommand{\TQBF}{\textprob{TQBF}} \newcommand{\LinProg}{\textprob{Linear Programming}} \newcommand{\LP}{\mathprob{LP}} \newcommand{\Factor}{\textprob{Factoring}} \newcommand{\CircVal}{\textprob{Circuit Value}} \newcommand{\CVAL}{\mathprob{CVAL}} \newcommand{\CircSat}{\textprob{Circuit Satisfiability}} \newcommand{\CSAT}{\textprob{CSAT}} \newcommand{\CycleCovers}{\textprob{Cycle Covers}} \newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}} \newcommand{\Reachability}{\textprob{Reachability}} \newcommand{\Unreachability}{\textprob{Unreachability}} \newcommand{\RCH}{\mathprob{RCH}} \newcommand{\BddHalt}{\textprob{Bounded Halting}} \newcommand{\BH}{\mathprob{BH}} \newcommand{\DiscreteLog}{\textprob{Discrete Log}} \newcommand{\REE}{\mathprob{REE}} \newcommand{\QBF}{\mathprob{QBF}} \newcommand{\MCSP}{\mathprob{MCSP}} \newcommand{\GGEO}{\mathprob{GGEO}} \newcommand{\CKTMIN}{\mathprob{CKT-MIN}} \newcommand{\MINCKT}{\mathprob{MIN-CKT}} \newcommand{\IdentityTest}{\textprob{Identity Testing}} \newcommand{\Majority}{\textprob{Majority}} \newcommand{\CountIndSets}{\textprob{\#Independent Sets}} \newcommand{\Parity}{\textprob{Parity}} \newcommand{\Clique}{\textprob{Clique}} \newcommand{\CountCycles}{\textprob{#Cycles}} \newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}} \newcommand{\CountMatchings}{\textprob{\#Matchings}} \newcommand{\CountMatch}{\mathprob{\#Matchings}} \newcommand{\ECSAT}{\mathprob{E#SAT}} \newcommand{\ShSAT}{\mathprob{#SAT}} \newcommand{\ShTSAT}{\mathprob{#3SAT}} \newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}} \newcommand{\Permanent}{\textprob{Permanent}} \newcommand{\ModPermanent}{\textprob{Modular Permanent}} \newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}} \newcommand{\GI}{\mathprob{GI}} \newcommand{\GNI}{\mathprob{GNI}} \newcommand{\GraphIso}{\textprob{Graph Isomorphism}} \newcommand{\QuantBoolForm}{\textprob{Quantified Boolean Formulae}} \newcommand{\GenGeography}{\textprob{Generalized Geography}} \newcommand{\MAXTSAT}{\mathprob{Max3SAT}} \newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}} \newcommand{\ELIN}{\mathprob{E3LIN2}} \newcommand{\CSP}{\mathprob{CSP}} \newcommand{\Lin}{\mathprob{Lin}} \newcommand{\ONE}{\mathbf{ONE}} \newcommand{\ZERO}{\mathbf{ZERO}} \newcommand{\yes} \newcommand{\no} $



〈前言〉

通往計算的現代綜合論之路





Our knowledge can only be finite, while our ignorance must necessarily be infinite.

我們的知識只能是有限的，同時我們的無知必定是無限的。

Karl Popper


2021年的秋天，歷經超過整整一年由新冠疫情帶來的封鎖，學校的大門終於再度敞開。當面見到了許久不見的老師、同學、還有只曾在電腦螢幕上看過的學生，在實體研討會和課堂上舉手發問，感受著琴房中三角鋼琴的觸鍵與音符在空氣中的震動。這些後疫情時代帶來的感官衝擊，除了讓人重拾對生活的熱情，也讓我開始認真省思和批判自已的學術研究。

也許從平時的隨筆(見附錄)中就可以嗅到一些蛛絲馬跡，雖然我很享受在純粹數學的邏輯世界中遨遊，但一直以來卻總是無法自制地不斷被其他領域吸引。我漸漸意識到相較於在數學理論的大廈上多鋪幾層磁磚，或許我更適合在不同領域間探索驚奇的連結與隱喻，並將所學所思帶回現實世界。

於是在歷經了一個短暫放逐自我的秋季學期(擔任了「科學與烹飪」的助教、修了音樂理論，並漸漸從幾個原本的研究合作中淡出)，我下定決心先從梳理幾年來在專業之外的所學作為起點，藉著學校每年一月資助研究生開設迷你課程的機會，以「計算是什麼？從圖靈機到黑洞和神經元」為題，從數學、物理、與生物三個視角，檢視自己本科的專業：電腦科學。在12位助教無償的自願協助，以及6位好友擔任客座講師之下，最終這個迷你課程以11堂主要課程、6堂客座演講，以及9堂延伸課程順利完結。

如今在博士畢業和踏往新領域(腦神經科學)的前夕，希望透過此書將當初迷你課程中的內容補齊、延展、修飾，除了讓這些知識有機會以輕鬆又不失專業的形式傳給更多潛在讀者，也作為自己破繭新生的紀念。

本書在講些什麼？

一提到“計算”這兩個字你會想到什麼？乍聽之下好像是個很蠢的問題，答案不是很顯而易見嗎？高中生可能會説計算就是根據數學公式算出各種方程式的解答。資工系學生可能會說計算就是寫個程式跑出想要的結果。這時候一個物理系的同學跳出來，說她最近看到一篇論文提到如何用計算問題的困難性來挑戰黑洞研究中的火牆悖論。另一個主修腦神經科學的同學也跟著插上話，大談果蠅腦中的神經元是如何計算出飛行方向。他們口中的“計算”真的是同樣的概念嗎？

在認真回答這個問題之前，我們勢必得先釐清這幾個觀點間的異同。因此本書將分為三大部份，依序剖析人造世界、物理世界和生物世界中的計算。

「稍等一下，為什麼這本書值得花力氣翻下去呢？」

本書能帶來的娛樂性當然無法和YouTube或Netflix相比。但如果你有耐心讀到這，並且已經被激起興趣，想要多知道時常出現在生活語境中的“計算”和數學、物理、生物等領域的關聯，那麼本書將會帶給你一趟深入淺出的三合一雲霄飛車之旅。

「那為什麼是人造世界、物理世界和生物世界這三種觀點？」

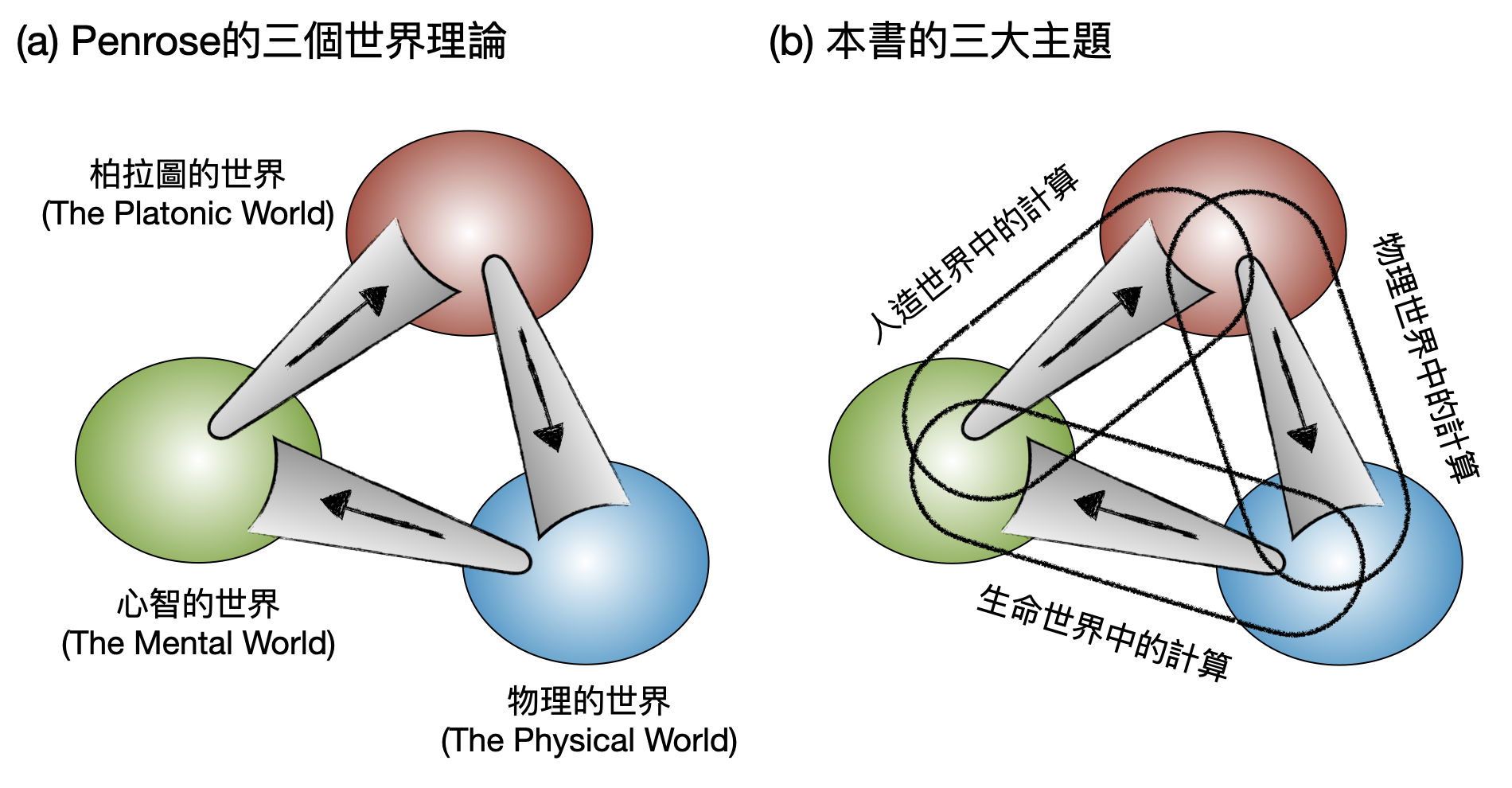
我想要從2020諾貝爾物理獎得主Roger Penrose在『通往真實的道路(The Road to Reality)』一書提到的「三個世界理論(The theory of three worlds)」談起。對於什麼是真實(reality)和存在(existence)這樣的問題，Penrose認為需要拆分為三個世界來討論(如下圖(a))：(1)柏拉圖的世界(the Platonic world)、(2)物理的世界(the physical world)和(3)心智的世界(the mental world)。人類從自身的心智世界，透過抽象思考的語言一窺由符號與想法組成的柏拉圖世界。而柏拉圖世界則支配了(部分的)物理世界的規則，最終物理世界承載了生命與我們的心靈。

本書的三大主題可以被理解為Penrose三個世界理論的“計算版本”(如上圖(b))：

人造世界中的計算討論心智世界和柏拉圖世界，以及前者創造與理解後者的過程。我們將看到圖靈機和其他的計算模型如何刻畫計算的機械過程、各式各樣的演算法如何描述內心的思路，還有計算的語言如何定義出新的形式化概念。

物理世界中的計算討論柏拉圖世界和物理世界，以及前者描述後者的過程。我們將看到四個不同的物理世界觀(古典、統計、量子、重力)，還有計算與它們互相影響的絕妙好戲。

生命世界中的計算討論物理世界和心智世界，以及前者湧現至後者的過程。我們將看到生命世界的不同層次如何承載各種計算，還有計算如何自然地從結構與隨機中湧現。

通往計算的現代綜合論之路

透過上述三個不同的角度，本書嘗試開闢一條通往計算的現代綜合論之路。這邊的“綜合論”指的是什麼？為什麼需要這樣的東西呢？

“計算”這個概念充斥著生活和科學研究中各個角落，受到歷史發展脈絡的影響，對於計算的研究和理解極度偏向使用來自數學的方法論。然而隨著越來越多的例子指出計算思維能夠在像是物理和生物這些不同的領域中注入新觀點，甚至反饋回數學這邊的計算理論，筆者認為是時候需要用一個更全面的角度來重新理解計算的本質。由於尚未有個具體的方法論被提出來，所以就姑且讓我們暫時稱之為計算的現代綜合論吧！

看到這裡，讀者也許還沒辦法體會上述“更全面的角度來重新理解計算的本質”是什麼意思，或是心裡感到半信半疑覺得這本書的作者是不是腦筋不太正常。沒關係，接下來三百多頁的內容就是要透過大量例子嘗試延展並支持這個觀點，希望在讀完後除了能讓你學到一些新東西之外，也可以稍微共鳴筆者撰寫本書的初衷。

如何閱讀本書

在寫作前，人們通常會建議想先清楚目標的讀者類型會是誰。國文作文考試時心中想的可能是閱卷老師喜歡學生引經據典，旅遊寫明信片時恨不得將所見所聞分享給親人朋友，學術寫作時則是擔心著哪邊可能又要被第二位審稿人誤解了。在本書構思初期，我想了好久，一直對於該選擇什麼類型的潛在讀者十分糾結。既希望能讓更多人能學到新東西，又在內容深度上有些拿捏不定。到底要寫的像是一般科普書那樣，著重在故事和科學家軼聞，還是要像教科書一次把細節給足？

最後，我決定走一條冒險的道路：先建立各學科的核心底層架構，接著注重在近代發展的宏觀故事。白話點來說，這本書將會是個無限自助吧，既會在不失專業和正確性的前提下帶著讀者建立一定程度的基礎，又會努力將各個領域發展前沿的奇珍異寶烹調成容易入口的山珍美味。由於本來就不可能期待每位走進自助吧的客人都會把所有食物吃一輪，在上菜之前，讓主廚先為您介紹針對不同背景的讀者，建議的享用方法：

大眾讀者： 這也許將會是近幾年來你看過最混亂複雜的一本書了，可能會像看克里斯多福·諾蘭(Christopher Nolan)的電影一般，讓人看到中間時仍摸不清頭緒。因此能懂多少就懂多少，可以把重心放在大方向的故事，以及試著從一些圖片中獲得感官上的享受。

對數理、科學具有強烈好奇心的中學生： 本書將會介於教科書和一般科普書籍及科學雜誌之間，在每個章節中都會先花一定的篇幅建立基礎思想架構，因此可能會有些陌生的符號讓你感到退縮。但千萬別因為害怕看不懂符號，而影響理解和學習。反之，我更希望這些迷惑可以激起你的好奇心，並成為之後進一步學習的動力！所以在閱讀本書時，在心態上可以像是去看一場職業棒球賽，雖然自己的體能和技術都還在發展階段，對於比賽中的細微操作也不甚瞭解，但是這個經驗將會打開你的視野，並且知道前方有什麼有趣的事物在等著你！

具有電腦科學或數理相關領域背景的大學生或社會人士： 本書的內容可能會讓你想起許多之前在課堂和教科書中的回憶，不過也許當初你在學這些東西時著重於細節的運算操作和考試等等，因此一直不知道學這些東西可以有什麼用。如果是這樣的話，本書將會把這些看似沒用的書中知識，放入幾十幾百年相關研究的脈絡發展之下，讓你能夠一窺大局的樣貌。雖然很高的機會這些知識對你的日常生活不會有太大的影響，然而在相關領域的前線發展上，你可能將會更看得出專家學者所做所言背後的脈絡，並且更不容易被一些華而不實的詞語呼弄過去！

相關領域內的專家： 在本書的三大主題之中，也許你已經是其中一個或是兩個的專家了，相關的內容可能對你來說十分輕鬆簡單，甚至會對我的敘事脈絡及主題選擇有些自己的看法。在這種情況下，我希望你可以用一個批判和省思的角度來看待本書，試著理解為什麼要把這麼多不同的主題放在同一個故事中，想想是否認同背後想要強調的大圖像，或是能否在讀完之後能更進一步有些啟發。

最後，本書三大主題的核心方法論分別是數學、物理和生物，因此在閱讀時建議讀者可以嘗試用不同的心態來享受：

數學的部份會有許多較長的故事軸，許多概念與想法被嚴密的邏輯串連起來，像是在下圍棋。第一次接觸時可能容易會被小細節卡住或分心。所以適時轉換視角的高低，將可以讓理解更為清晰。

物理的部份則像是進入了迪士尼樂園，不同園區有著相似但又不太一樣的世界觀設定。花時間咀嚼各個世界觀背後的緣起和思想，將可以讓遊客更能發現樂園中設計的巧思。

生物的部份有點像是我最喜歡的桌遊：拼圖。透過大量的例子，我們將蒐集到許多看似分散的碎片，但是時間一久，便逐漸能拼出一塊一塊的小區域，並漸漸越來越能看出宏觀的面貌。

如何面對書中的數學公式、譬喻故事、與專有名詞？

為了能在呈現學問真實面貌和平易近人之間找到平衡，本書將同時有著具體的數學公式、有趣但可能稍微在嚴謹程度上不精確的譬喻故事以及各種專有名詞。不同讀者必定會對這三種元素有不一樣的接受程度，甚至對其中幾個會略有反感。

在這邊我鼓勵讀者可以嘗試小小跨出舒適圈。例如，試著將愛因斯坦場方程式中的符號，在形式上對應到物理直覺中的時空圖像。或是在譬喻故事中釐清是哪個部份不完全正確，並試著找出更好的解釋方法。至於複雜的人名與專有名詞，就當作在訓練出國旅遊時如何自動忽略招牌上看不懂的字的能力吧！

啟程

我曾一度迷失在無止境的哲學思考中，糾結於方法論在抽象層次上的優劣，或是對讀到的研究和知識總是有過多的批判。直到我的博士指導老師Boaz有一天突然跟我說，有時候或許別太像個哲學家，要有實際行動才能做出進展。Boaz的一席話，點醒了當時陷入無限迴圈的我，重新意識到坐而言不如起而行的重要。

於是這本書對我來說是一趟新旅程的起點，透過整理所學所想，淬煉出更清晰的視界。希望本書也能帶給一些年輕讀者對於相關知識的好奇與啟蒙，讓我們出發吧！