$
\newcommand{\undefined}{}
\newcommand{\hfill}{}
\newcommand{\qedhere}{\square}
\newcommand{\qed}{\square}
\newcommand{\ensuremath}[1]{#1}
\newcommand{\bit}{\{0,1\}}
\newcommand{\Bit}{\{-1,1\}}
\newcommand{\Stab}{\mathbf{Stab}}
\newcommand{\NS}{\mathbf{NS}}
\newcommand{\ba}{\mathbf{a}}
\newcommand{\bc}{\mathbf{c}}
\newcommand{\bd}{\mathbf{d}}
\newcommand{\be}{\mathbf{e}}
\newcommand{\bh}{\mathbf{h}}
\newcommand{\br}{\mathbf{r}}
\newcommand{\bs}{\mathbf{s}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\Var}{\mathbf{Var}}
\newcommand{\dist}{\text{dist}}
\newcommand{\norm}[1]{\\|#1\\|}
\newcommand{\etal}
\newcommand{\ie}
\newcommand{\eg}
\newcommand{\cf}
\newcommand{\rank}{\text{rank}}
\newcommand{\tr}{\text{tr}}
\newcommand{\mor}{\text{Mor}}
\newcommand{\hom}{\text{Hom}}
\newcommand{\id}{\text{id}}
\newcommand{\obj}{\text{obj}}
\newcommand{\pr}{\text{pr}}
\newcommand{\ker}{\text{ker}}
\newcommand{\coker}{\text{coker}}
\newcommand{\im}{\text{im}}
\newcommand{\vol}{\text{vol}}
\newcommand{\disc}{\text{disc}}
\newcommand{\bbA}{\mathbb A}
\newcommand{\bbB}{\mathbb B}
\newcommand{\bbC}{\mathbb C}
\newcommand{\bbD}{\mathbb D}
\newcommand{\bbE}{\mathbb E}
\newcommand{\bbF}{\mathbb F}
\newcommand{\bbG}{\mathbb G}
\newcommand{\bbH}{\mathbb H}
\newcommand{\bbI}{\mathbb I}
\newcommand{\bbJ}{\mathbb J}
\newcommand{\bbK}{\mathbb K}
\newcommand{\bbL}{\mathbb L}
\newcommand{\bbM}{\mathbb M}
\newcommand{\bbN}{\mathbb N}
\newcommand{\bbO}{\mathbb O}
\newcommand{\bbP}{\mathbb P}
\newcommand{\bbQ}{\mathbb Q}
\newcommand{\bbR}{\mathbb R}
\newcommand{\bbS}{\mathbb S}
\newcommand{\bbT}{\mathbb T}
\newcommand{\bbU}{\mathbb U}
\newcommand{\bbV}{\mathbb V}
\newcommand{\bbW}{\mathbb W}
\newcommand{\bbX}{\mathbb X}
\newcommand{\bbY}{\mathbb Y}
\newcommand{\bbZ}{\mathbb Z}
\newcommand{\sA}{\mathscr A}
\newcommand{\sB}{\mathscr B}
\newcommand{\sC}{\mathscr C}
\newcommand{\sD}{\mathscr D}
\newcommand{\sE}{\mathscr E}
\newcommand{\sF}{\mathscr F}
\newcommand{\sG}{\mathscr G}
\newcommand{\sH}{\mathscr H}
\newcommand{\sI}{\mathscr I}
\newcommand{\sJ}{\mathscr J}
\newcommand{\sK}{\mathscr K}
\newcommand{\sL}{\mathscr L}
\newcommand{\sM}{\mathscr M}
\newcommand{\sN}{\mathscr N}
\newcommand{\sO}{\mathscr O}
\newcommand{\sP}{\mathscr P}
\newcommand{\sQ}{\mathscr Q}
\newcommand{\sR}{\mathscr R}
\newcommand{\sS}{\mathscr S}
\newcommand{\sT}{\mathscr T}
\newcommand{\sU}{\mathscr U}
\newcommand{\sV}{\mathscr V}
\newcommand{\sW}{\mathscr W}
\newcommand{\sX}{\mathscr X}
\newcommand{\sY}{\mathscr Y}
\newcommand{\sZ}{\mathscr Z}
\newcommand{\sfA}{\mathsf A}
\newcommand{\sfB}{\mathsf B}
\newcommand{\sfC}{\mathsf C}
\newcommand{\sfD}{\mathsf D}
\newcommand{\sfE}{\mathsf E}
\newcommand{\sfF}{\mathsf F}
\newcommand{\sfG}{\mathsf G}
\newcommand{\sfH}{\mathsf H}
\newcommand{\sfI}{\mathsf I}
\newcommand{\sfJ}{\mathsf J}
\newcommand{\sfK}{\mathsf K}
\newcommand{\sfL}{\mathsf L}
\newcommand{\sfM}{\mathsf M}
\newcommand{\sfN}{\mathsf N}
\newcommand{\sfO}{\mathsf O}
\newcommand{\sfP}{\mathsf P}
\newcommand{\sfQ}{\mathsf Q}
\newcommand{\sfR}{\mathsf R}
\newcommand{\sfS}{\mathsf S}
\newcommand{\sfT}{\mathsf T}
\newcommand{\sfU}{\mathsf U}
\newcommand{\sfV}{\mathsf V}
\newcommand{\sfW}{\mathsf W}
\newcommand{\sfX}{\mathsf X}
\newcommand{\sfY}{\mathsf Y}
\newcommand{\sfZ}{\mathsf Z}
\newcommand{\cA}{\mathcal A}
\newcommand{\cB}{\mathcal B}
\newcommand{\cC}{\mathcal C}
\newcommand{\cD}{\mathcal D}
\newcommand{\cE}{\mathcal E}
\newcommand{\cF}{\mathcal F}
\newcommand{\cG}{\mathcal G}
\newcommand{\cH}{\mathcal H}
\newcommand{\cI}{\mathcal I}
\newcommand{\cJ}{\mathcal J}
\newcommand{\cK}{\mathcal K}
\newcommand{\cL}{\mathcal L}
\newcommand{\cM}{\mathcal M}
\newcommand{\cN}{\mathcal N}
\newcommand{\cO}{\mathcal O}
\newcommand{\cP}{\mathcal P}
\newcommand{\cQ}{\mathcal Q}
\newcommand{\cR}{\mathcal R}
\newcommand{\cS}{\mathcal S}
\newcommand{\cT}{\mathcal T}
\newcommand{\cU}{\mathcal U}
\newcommand{\cV}{\mathcal V}
\newcommand{\cW}{\mathcal W}
\newcommand{\cX}{\mathcal X}
\newcommand{\cY}{\mathcal Y}
\newcommand{\cZ}{\mathcal Z}
\newcommand{\bfA}{\mathbf A}
\newcommand{\bfB}{\mathbf B}
\newcommand{\bfC}{\mathbf C}
\newcommand{\bfD}{\mathbf D}
\newcommand{\bfE}{\mathbf E}
\newcommand{\bfF}{\mathbf F}
\newcommand{\bfG}{\mathbf G}
\newcommand{\bfH}{\mathbf H}
\newcommand{\bfI}{\mathbf I}
\newcommand{\bfJ}{\mathbf J}
\newcommand{\bfK}{\mathbf K}
\newcommand{\bfL}{\mathbf L}
\newcommand{\bfM}{\mathbf M}
\newcommand{\bfN}{\mathbf N}
\newcommand{\bfO}{\mathbf O}
\newcommand{\bfP}{\mathbf P}
\newcommand{\bfQ}{\mathbf Q}
\newcommand{\bfR}{\mathbf R}
\newcommand{\bfS}{\mathbf S}
\newcommand{\bfT}{\mathbf T}
\newcommand{\bfU}{\mathbf U}
\newcommand{\bfV}{\mathbf V}
\newcommand{\bfW}{\mathbf W}
\newcommand{\bfX}{\mathbf X}
\newcommand{\bfY}{\mathbf Y}
\newcommand{\bfZ}{\mathbf Z}
\newcommand{\rmA}{\mathrm A}
\newcommand{\rmB}{\mathrm B}
\newcommand{\rmC}{\mathrm C}
\newcommand{\rmD}{\mathrm D}
\newcommand{\rmE}{\mathrm E}
\newcommand{\rmF}{\mathrm F}
\newcommand{\rmG}{\mathrm G}
\newcommand{\rmH}{\mathrm H}
\newcommand{\rmI}{\mathrm I}
\newcommand{\rmJ}{\mathrm J}
\newcommand{\rmK}{\mathrm K}
\newcommand{\rmL}{\mathrm L}
\newcommand{\rmM}{\mathrm M}
\newcommand{\rmN}{\mathrm N}
\newcommand{\rmO}{\mathrm O}
\newcommand{\rmP}{\mathrm P}
\newcommand{\rmQ}{\mathrm Q}
\newcommand{\rmR}{\mathrm R}
\newcommand{\rmS}{\mathrm S}
\newcommand{\rmT}{\mathrm T}
\newcommand{\rmU}{\mathrm U}
\newcommand{\rmV}{\mathrm V}
\newcommand{\rmW}{\mathrm W}
\newcommand{\rmX}{\mathrm X}
\newcommand{\rmY}{\mathrm Y}
\newcommand{\rmZ}{\mathrm Z}
\newcommand{\bb}{\mathbf{b}}
\newcommand{\bv}{\mathbf{v}}
\newcommand{\bw}{\mathbf{w}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\paren}[1]{( #1 )}
\newcommand{\Paren}[1]{\left( #1 \right)}
\newcommand{\bigparen}[1]{\bigl( #1 \bigr)}
\newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)}
\newcommand{\biggparen}[1]{\biggl( #1 \biggr)}
\newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)}
\newcommand{\abs}[1]{\lvert #1 \rvert}
\newcommand{\Abs}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\card}[1]{\left| #1 \right|}
\newcommand{\Card}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\norm}[1]{\lVert #1 \rVert}
\newcommand{\Norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert}
\newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert}
\newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert}
\newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\Iprod}[1]{\left\langle #1 \right\rangle}
\newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle}
\newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle}
\newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle}
\newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle}
\newcommand{\set}[1]{\lbrace #1 \rbrace}
\newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace}
\newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace}
\newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace}
\newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace}
\newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace}
\newcommand{\bracket}[1]{\lbrack #1 \rbrack}
\newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack}
\newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack}
\newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack}
\newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack}
\newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack}
\newcommand{\ucorner}[1]{\ulcorner #1 \urcorner}
\newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner}
\newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner}
\newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner}
\newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner}
\newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner}
\newcommand{\ceil}[1]{\lceil #1 \rceil}
\newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil}
\newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil}
\newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil}
\newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil}
\newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil}
\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor}
\newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor}
\newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor}
\newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor}
\newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor}
\newcommand{\lcorner}[1]{\llcorner #1 \lrcorner}
\newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner}
\newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner}
\newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner}
\newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner}
\newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner}
\newcommand{\ket}[1]{| #1 \rangle}
\newcommand{\bra}[1]{\langle #1 |}
\newcommand{\braket}[2]{\langle #1 | #2 \rangle}
\newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |}
\newcommand{\e}{\varepsilon}
\newcommand{\eps}{\varepsilon}
\newcommand{\from}{\colon}
\newcommand{\super}[2]{#1^{(#2)}}
\newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}}
\newcommand{\tensor}{\otimes}
\newcommand{\eset}{\emptyset}
\newcommand{\sse}{\subseteq}
\newcommand{\sst}{\substack}
\newcommand{\ot}{\otimes}
\newcommand{\Esst}[1]{\bbE_{\substack{#1}}}
\newcommand{\vbig}{\vphantom{\bigoplus}}
\newcommand{\seteq}{\mathrel{\mathop:}=}
\newcommand{\defeq}{\stackrel{\mathrm{def}}=}
\newcommand{\Mid}{\mathrel{}\middle|\mathrel{}}
\newcommand{\Ind}{\mathbf 1}
\newcommand{\bits}{\{0,1\}}
\newcommand{\sbits}{\{\pm 1\}}
\newcommand{\R}{\mathbb R}
\newcommand{\Rnn}{\R_{\ge 0}}
\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\C}{\mathbb C}
\newcommand{\A}{\mathbb A}
\newcommand{\Real}{\mathbb R}
\newcommand{\mper}{\,.}
\newcommand{\mcom}{\,,}
\DeclareMathOperator{\Id}{Id}
\DeclareMathOperator{\cone}{cone}
\DeclareMathOperator{\vol}{vol}
\DeclareMathOperator{\val}{val}
\DeclareMathOperator{\opt}{opt}
\DeclareMathOperator{\Opt}{Opt}
\DeclareMathOperator{\Val}{Val}
\DeclareMathOperator{\LP}{LP}
\DeclareMathOperator{\SDP}{SDP}
\DeclareMathOperator{\Tr}{Tr}
\DeclareMathOperator{\Inf}{Inf}
\DeclareMathOperator{\size}{size}
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\min}{min}
\DeclareMathOperator{\max}{max}
\DeclareMathOperator{\argmax}{arg\,max}
\DeclareMathOperator{\argmin}{arg\,min}
\DeclareMathOperator{\qpoly}{qpoly}
\DeclareMathOperator{\qqpoly}{qqpoly}
\DeclareMathOperator{\conv}{conv}
\DeclareMathOperator{\Conv}{Conv}
\DeclareMathOperator{\supp}{supp}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\perm}{perm}
\DeclareMathOperator{\mspan}{span}
\DeclareMathOperator{\mrank}{rank}
\DeclareMathOperator{\E}{\mathbb E}
\DeclareMathOperator{\pE}{\tilde{\mathbb E}}
\DeclareMathOperator{\Pr}{\mathbb P}
\DeclareMathOperator{\Span}{Span}
\DeclareMathOperator{\Cone}{Cone}
\DeclareMathOperator{\junta}{junta}
\DeclareMathOperator{\NSS}{NSS}
\DeclareMathOperator{\SA}{SA}
\DeclareMathOperator{\SOS}{SOS}
\DeclareMathOperator{\Stab}{\mathbf Stab}
\DeclareMathOperator{\Det}{\textbf{Det}}
\DeclareMathOperator{\Perm}{\textbf{Perm}}
\DeclareMathOperator{\Sym}{\textbf{Sym}}
\DeclareMathOperator{\Pow}{\textbf{Pow}}
\DeclareMathOperator{\Gal}{\textbf{Gal}}
\DeclareMathOperator{\Aut}{\textbf{Aut}}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\cE}{\mathcal{E}}
\newcommand{\E}{\mathbb{E}}
\newcommand{\pE}{\tilde{\mathbb{E}}}
\newcommand{\N}{\mathbb{N}}
\renewcommand{\P}{\mathcal{P}}
\notag
$
$
\newcommand{\sleq}{\ensuremath{\preceq}}
\newcommand{\sgeq}{\ensuremath{\succeq}}
\newcommand{\diag}{\ensuremath{\mathrm{diag}}}
\newcommand{\support}{\ensuremath{\mathrm{support}}}
\newcommand{\zo}{\ensuremath{\{0,1\}}}
\newcommand{\pmo}{\ensuremath{\{\pm 1\}}}
\newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}}
\newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}}
\newcommand{\rank}{\ensuremath{\mathrm{rank}}}
\newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}}
\newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}}
\newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}}
\newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}}
\newcommand{\eqdef}{\ensuremath{ =^{def}}}
\newcommand{\threshold}{\ensuremath{\mathrm{threshold}}}
\newcommand{\vbls}{\ensuremath{\mathrm{vbls}}}
\newcommand{\cons}{\ensuremath{\mathrm{cons}}}
\newcommand{\edges}{\ensuremath{\mathrm{edges}}}
\newcommand{\cl}{\ensuremath{\mathrm{cl}}}
\newcommand{\xor}{\ensuremath{\oplus}}
\newcommand{\1}{\ensuremath{\mathrm{1}}}
\notag
$
$
\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}}
\newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}}
\newcommand{\nchoose}[1]{\ensuremath}
\newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}}
\notag
$
$
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}
\newcommand{\R} % real numbers
\newcommand{\N}} % natural numbers
\newcommand{\Z} % integers
\newcommand{\F} % a field
\newcommand{\Q} % the rationals
\newcommand{\C}{\mathbb{C}} % the complexes
\newcommand{\poly}}
\newcommand{\polylog}}
\newcommand{\loglog}}}
\newcommand{\zo}{\{0,1\}}
\newcommand{\suchthat}
\newcommand{\pr}[1]{\Pr\left[#1\right]}
\newcommand{\deffont}{\em}
\newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}
\newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation
\newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance
\newcommand{\xor}{\oplus}
\newcommand{\GF}{\mathrm{GF}}
\newcommand{\eps}{\varepsilon}
\notag
$
$
\newcommand{\class}[1]{\mathbf{#1}}
\newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements
\newcommand{\BPP}{\class{BPP}}
\newcommand{\NP}{\class{NP}}
\newcommand{\RP}{\class{RP}}
\newcommand{\coRP}{\coclass{RP}}
\newcommand{\ZPP}{\class{ZPP}}
\newcommand{\BQP}{\class{BQP}}
\newcommand{\FP}{\class{FP}}
\newcommand{\QP}{\class{QuasiP}}
\newcommand{\VF}{\class{VF}}
\newcommand{\VBP}{\class{VBP}}
\newcommand{\VP}{\class{VP}}
\newcommand{\VNP}{\class{VNP}}
\newcommand{\RNC}{\class{RNC}}
\newcommand{\RL}{\class{RL}}
\newcommand{\BPL}{\class{BPL}}
\newcommand{\coRL}{\coclass{RL}}
\newcommand{\IP}{\class{IP}}
\newcommand{\AM}{\class{AM}}
\newcommand{\MA}{\class{MA}}
\newcommand{\QMA}{\class{QMA}}
\newcommand{\SBP}{\class{SBP}}
\newcommand{\coAM}{\class{coAM}}
\newcommand{\coMA}{\class{coMA}}
\renewcommand{\P}{\class{P}}
\newcommand\prBPP{\class{prBPP}}
\newcommand\prRP{\class{prRP}}
\newcommand\prP{\class{prP}}
\newcommand{\Ppoly}{\class{P/poly}}
\newcommand{\NPpoly}{\class{NP/poly}}
\newcommand{\coNPpoly}{\class{coNP/poly}}
\newcommand{\DTIME}{\class{DTIME}}
\newcommand{\TIME}{\class{TIME}}
\newcommand{\SIZE}{\class{SIZE}}
\newcommand{\SPACE}{\class{SPACE}}
\newcommand{\ETIME}{\class{E}}
\newcommand{\BPTIME}{\class{BPTIME}}
\newcommand{\RPTIME}{\class{RPTIME}}
\newcommand{\ZPTIME}{\class{ZPTIME}}
\newcommand{\EXP}{\class{EXP}}
\newcommand{\ZPEXP}{\class{ZPEXP}}
\newcommand{\RPEXP}{\class{RPEXP}}
\newcommand{\BPEXP}{\class{BPEXP}}
\newcommand{\SUBEXP}{\class{SUBEXP}}
\newcommand{\NTIME}{\class{NTIME}}
\newcommand{\NL}{\class{NL}}
\renewcommand{\L}{\class{L}}
\newcommand{\NQP}{\class{NQP}}
\newcommand{\NEXP}{\class{NEXP}}
\newcommand{\coNEXP}{\coclass{NEXP}}
\newcommand{\NPSPACE}{\class{NPSPACE}}
\newcommand{\PSPACE}{\class{PSPACE}}
\newcommand{\NSPACE}{\class{NSPACE}}
\newcommand{\coNSPACE}{\coclass{NSPACE}}
\newcommand{\coL}{\coclass{L}}
\newcommand{\coP}{\coclass{P}}
\newcommand{\coNP}{\coclass{NP}}
\newcommand{\coNL}{\coclass{NL}}
\newcommand{\coNPSPACE}{\coclass{NPSPACE}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\LINSPACE}{\class{LINSPACE}}
\newcommand{\qP}{\class{\tilde{P}}}
\newcommand{\PH}{\class{PH}}
\newcommand{\EXPSPACE}{\class{EXPSPACE}}
\newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}}
\newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}}
\newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}}
\newcommand{\PiP}[1]{\class{\Pi_{#1}P}}
\newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}}
\newcommand{\ATIME}{\class{ATIME}}
\newcommand{\ASPACE}{\class{ASPACE}}
\newcommand{\AP}{\class{AP}}
\newcommand{\AL}{\class{AL}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\VNC}[1]{\class{VNC^{#1}}}
\newcommand{\NC}[1]{\class{NC^{#1}}}
\newcommand{\AC}[1]{\class{AC^{#1}}}
\newcommand{\ACC}[1]{\class{ACC^{#1}}}
\newcommand{\TC}[1]{\class{TC^{#1}}}
\newcommand{\ShP}{\class{\# P}}
\newcommand{\PaP}{\class{\oplus P}}
\newcommand{\PCP}{\class{PCP}}
\newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}}
\newcommand{\MIP}{\class{MIP}}
$
$
\newcommand{\textprob}[1]{\text{#1}}
\newcommand{\mathprob}[1]{\textbf{#1}}
\newcommand{\Satisfiability}{\textprob{Satisfiability}}
\newcommand{\SAT}{\textprob{SAT}}
\newcommand{\TSAT}{\textprob{3SAT}}
\newcommand{\USAT}{\textprob{USAT}}
\newcommand{\UNSAT}{\textprob{UNSAT}}
\newcommand{\QPSAT}{\textprob{QPSAT}}
\newcommand{\TQBF}{\textprob{TQBF}}
\newcommand{\LinProg}{\textprob{Linear Programming}}
\newcommand{\LP}{\mathprob{LP}}
\newcommand{\Factor}{\textprob{Factoring}}
\newcommand{\CircVal}{\textprob{Circuit Value}}
\newcommand{\CVAL}{\mathprob{CVAL}}
\newcommand{\CircSat}{\textprob{Circuit Satisfiability}}
\newcommand{\CSAT}{\textprob{CSAT}}
\newcommand{\CycleCovers}{\textprob{Cycle Covers}}
\newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}}
\newcommand{\Reachability}{\textprob{Reachability}}
\newcommand{\Unreachability}{\textprob{Unreachability}}
\newcommand{\RCH}{\mathprob{RCH}}
\newcommand{\BddHalt}{\textprob{Bounded Halting}}
\newcommand{\BH}{\mathprob{BH}}
\newcommand{\DiscreteLog}{\textprob{Discrete Log}}
\newcommand{\REE}{\mathprob{REE}}
\newcommand{\QBF}{\mathprob{QBF}}
\newcommand{\MCSP}{\mathprob{MCSP}}
\newcommand{\GGEO}{\mathprob{GGEO}}
\newcommand{\CKTMIN}{\mathprob{CKT-MIN}}
\newcommand{\MINCKT}{\mathprob{MIN-CKT}}
\newcommand{\IdentityTest}{\textprob{Identity Testing}}
\newcommand{\Majority}{\textprob{Majority}}
\newcommand{\CountIndSets}{\textprob{\#Independent Sets}}
\newcommand{\Parity}{\textprob{Parity}}
\newcommand{\Clique}{\textprob{Clique}}
\newcommand{\CountCycles}{\textprob{#Cycles}}
\newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}}
\newcommand{\CountMatchings}{\textprob{\#Matchings}}
\newcommand{\CountMatch}{\mathprob{\#Matchings}}
\newcommand{\ECSAT}{\mathprob{E#SAT}}
\newcommand{\ShSAT}{\mathprob{#SAT}}
\newcommand{\ShTSAT}{\mathprob{#3SAT}}
\newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}}
\newcommand{\Permanent}{\textprob{Permanent}}
\newcommand{\ModPermanent}{\textprob{Modular Permanent}}
\newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}}
\newcommand{\GI}{\mathprob{GI}}
\newcommand{\GNI}{\mathprob{GNI}}
\newcommand{\GraphIso}{\textprob{Graph Isomorphism}}
\newcommand{\QuantBoolForm}{\textprob{Quantified Boolean
Formulae}}
\newcommand{\GenGeography}{\textprob{Generalized Geography}}
\newcommand{\MAXTSAT}{\mathprob{Max3SAT}}
\newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}}
\newcommand{\ELIN}{\mathprob{E3LIN2}}
\newcommand{\CSP}{\mathprob{CSP}}
\newcommand{\Lin}{\mathprob{Lin}}
\newcommand{\ONE}{\mathbf{ONE}}
\newcommand{\ZERO}{\mathbf{ZERO}}
\newcommand{\yes}
\newcommand{\no}
$
$\Det_n$ is $\VBP$-complete
In this note, we are going to prove that $\Det_n$ is $\VBP$-complete under polynomial-size projection. In the following, we will start from the simpler direction: every polynomial $f\in\VBP$ can be reduced to $\Det_n$ via polynomial-size projection. Next, we will show that $\Det_n\in\VBP$.
$\VBP$s reduce to $\Det_n$
W.l.o.g., let’s consider the case where all the edges between each layer are assigned a variable. Concretely, the variables are $x^{(1)},x^{(2)},\dots,x^{(d)}$ where $x^{(1)},x^{(d)}$ are $n$-dimensional vectors and the rest are $n\times n$ matrices. The output of the arithmetic branching program (ABP) is the sum of all the path from the source vertex to the terminal vertex, i.e.,
\begin{equation}
\sum_{1\leq i_1,i_2,\dots,i_d\leq n}x^{(1)}_{i_1}x^{(2)}_{i_1i_2}\cdots x^{(d-1)}_{i_{d-2}i_{d-1}}x^{(d)}_{i_d}.
\end{equation}
Now, the idea is to construct a graph $G$ such that a cycle cover in $G$ corresponds to exactly one unique path in the arithmetic branching program. Moreover, the sign of the cycle cover should be the same so that the sum would be the determinant value of the adjacency matrix of $G$. The construction of $G$ is actually quite simple with the following three steps:
- Each vertex in the arithmetic branching program (including the source $s$ and the terminal $t$) corresponds to a vertex in $G$ and the edge between the vertex in the program corresponds to an (directed) edge between the vertices in $G$.
- Add an edge from $t$ to $s$ with weight $1$.
- Add an self-loop with weight $1$ for each vertex (without $s$ and $t$).
Note that the reduction is polynomial-size. Now, we have the following observation.
- A cycle cover in $G$ must contains the edge from $t$ to $s$.
- As a result, a cycle cover in $G$ exactly contains one path from $s$ to $t$.
- The number of cycles in each cycle cover is the same and thus the sign is the same.
Finally, we conclude that the determinant of the adjacency matrix of $G$ is either the value of the arithmetic branching program or the negative of that.
$\Det_n\in\VBP$
The goal of this section is to construct a polynomial-size ABP for $\Det_n$. Note that there’s a trivial exponential-size ABP since determinant can be written as the sum of exponentially many monomials.
As there are exponentially many monomials in the determinant function, we should exploit its structure to build a smaller ABP. Recall once we view the entries of the input matrix as the weight of the edges of a directed graph with $n$ vertices, the determinant is simply the signed weighted sum of cycle covers of that graph. Concretely, given $A\in\mathbb{F}^2$, let $G_A$ be the corresponding graph, we have
\begin{equation}
\text{det}(A) = \sum_{\mathcal{C}\in\mathcal{CS}(G_A)}\text{sign}(\mathcal{C})\cdot\text{wt}(\mathcal{C}),
\end{equation}
where $\mathcal{CS}(G_A)$ is the set of all possible cycle covers for $G_A$.
With this beautilful connection, a naive approach is to construct an ABP such that each path from the source to the terminal corresponds to a cycle cover of $G_A$. However, one can soon find out that this is non-trivial since it is difficult to avoid variables in the same row of $A$ appear on the same path in the ABP. Mahajan and Vinay circumvent this issue basedon the clow sequence, which is a variant of cycle cover. Intuitively, they first showed that the signed weighted sum over the clow sequences of a graph is exactly the determinant of its adjacency matrix. Next, they constructed a polynomial-size (concretely, O(n^3) size) ABP that computes the signed weighted sum over the clow sequences. These two steps together imply that $\Det_n\in\VBP$.
Clow sequence
Let $G$ be a graph with vertex set $V(G)$. A clow $C$ of $G$ is a sequence of vertices $v_1,\dots,v_{\ell}$ such that $v_1\leq v_i$ for $i=2,\dots,\ell$. Denote $\text{head}(C)=v_1$ and the length of $C$ as $|C|=\ell$. A clow sequence $\mathcal{C}$ of $G$ is a sequence of clows $(C_1,C_2,\dots,C_r)$ such that $\text{head}(C_1)<\text{head}(C_2)<\cdots<\text{head}(C_r)$. Denote the length of $\mathcal{C}$ as $|\mathcal{C}|=\sum_{i\in[r]}=|C_i|$. The sign of $\mathcal{C}$ is defined as $(-1)^{|\mathcal{C}|+r}$.
The following is an example of a clow sequence of $[5]$.
Intuition
$\Det_n(A)$ is equal to the sum over clow sequence of $G_A$
First, observe that a cycle cover is a clow sequence and the signs of the two are the same. Next, we are going to see that the rest of the clow sequences will cancell out each other. Note that if a clow sequence $\mathcal{C}=(C_1,C_2,\dots,C_r)$ is not a cycle cover, then there must exists a vertex $v\in V(G)$ such that $v$ appears more than once in $\mathcal{C}$. Let’s focus on the first vertex that appears more than once starting from the last clow $C_r$ and proceeding backwards. There are two possible cases:
- The first two appearances of $v$ are in different clows.
- The first two appearances of $v$ are in the same clow.
The key observation of Mahajan and Vinay is that there exists an isomorphism between the two cases. Furthermore, the signs of the two clow sequences that are isomorphic have different signs. That is, they will cancel out each other.
In the following, we are going to see the isomorphism between these two cases.
From 1 to 2, let $C_i$ and $C_{i+1}$ be the clows that contain $v$ where $C_i=(a_1,\dots,\cdots,v,\cdots,a_{t})$ and $C_{i+1}=(b_1,\dots,b_{j},v,b_{j+2},\cdot,b_{t’})$. Define a new clow as $C’=(a_1,\cdots,v,b_{j+2},\cdots,b_{j},v,\cdot,a_t)$. Note that as $a_1<b_1$, we know that every elements in $C_i’$ is greater than $a_1$ and thus $C_i’$ is indeed a clow. Also, the new clow sequence is in type 2 and $C’$ is the first clow that contains a repeated vertex.
Note that the construction is invertible. From 2 to 1, let $C_i=(a_1,\dots,v,b_{j+2},\cdots,b_{j},v,\dots,a_t)$, define $C_i’=(a_1,\dots,v,\dots,a_t)$ and $C_{i+1}’=(b_1,\dots,v,\dots,b_{t’})$. One can see that the new clow sequence that contains $C_i’$ and $C_{i+1}’$ is a valid type 1 clow sequence. Furthermore, the construction is isomorphic. See the following figure for illustration.
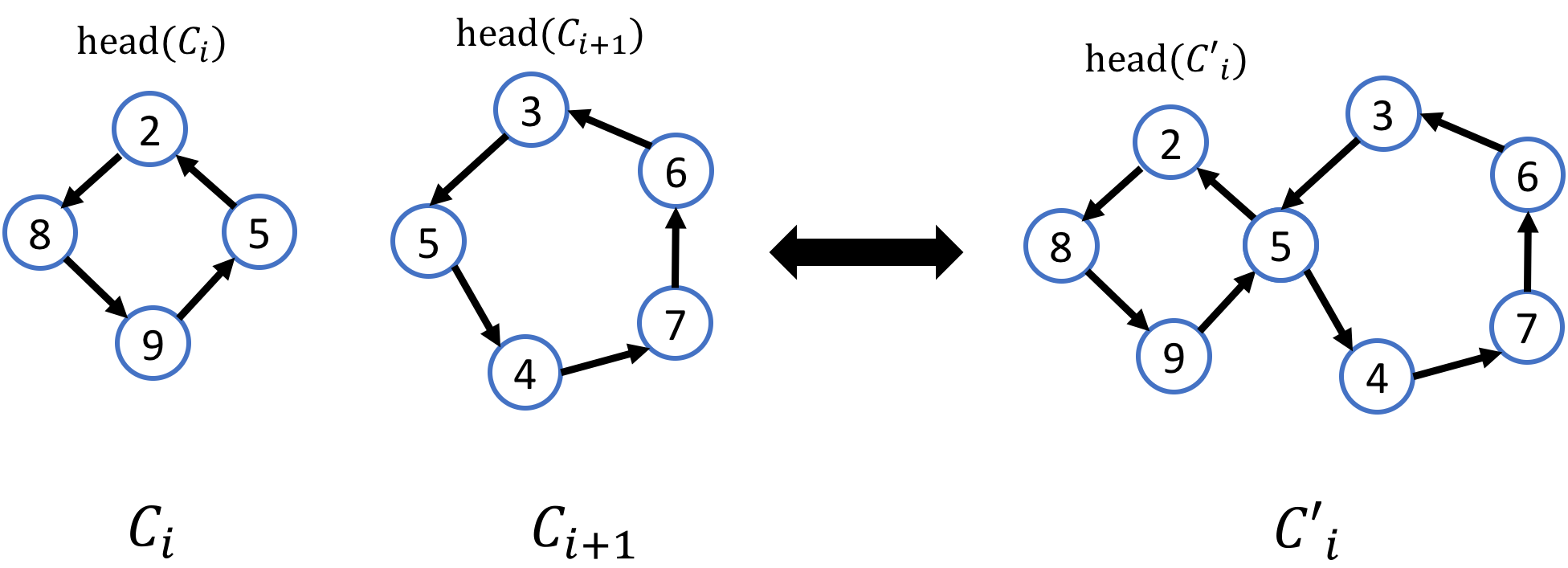
Construct polynomial-size ABP computes the sum over clow sequence
