$
\newcommand{\undefined}{}
\newcommand{\hfill}{}
\newcommand{\qedhere}{\square}
\newcommand{\qed}{\square}
\newcommand{\ensuremath}[1]{#1}
\newcommand{\bit}{\{0,1\}}
\newcommand{\Bit}{\{-1,1\}}
\newcommand{\Stab}{\mathbf{Stab}}
\newcommand{\NS}{\mathbf{NS}}
\newcommand{\ba}{\mathbf{a}}
\newcommand{\bc}{\mathbf{c}}
\newcommand{\bd}{\mathbf{d}}
\newcommand{\be}{\mathbf{e}}
\newcommand{\bh}{\mathbf{h}}
\newcommand{\br}{\mathbf{r}}
\newcommand{\bs}{\mathbf{s}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\Var}{\mathbf{Var}}
\newcommand{\dist}{\text{dist}}
\newcommand{\norm}[1]{\\|#1\\|}
\newcommand{\etal}
\newcommand{\ie}
\newcommand{\eg}
\newcommand{\cf}
\newcommand{\rank}{\text{rank}}
\newcommand{\tr}{\text{tr}}
\newcommand{\mor}{\text{Mor}}
\newcommand{\hom}{\text{Hom}}
\newcommand{\id}{\text{id}}
\newcommand{\obj}{\text{obj}}
\newcommand{\pr}{\text{pr}}
\newcommand{\ker}{\text{ker}}
\newcommand{\coker}{\text{coker}}
\newcommand{\im}{\text{im}}
\newcommand{\vol}{\text{vol}}
\newcommand{\disc}{\text{disc}}
\newcommand{\bbA}{\mathbb A}
\newcommand{\bbB}{\mathbb B}
\newcommand{\bbC}{\mathbb C}
\newcommand{\bbD}{\mathbb D}
\newcommand{\bbE}{\mathbb E}
\newcommand{\bbF}{\mathbb F}
\newcommand{\bbG}{\mathbb G}
\newcommand{\bbH}{\mathbb H}
\newcommand{\bbI}{\mathbb I}
\newcommand{\bbJ}{\mathbb J}
\newcommand{\bbK}{\mathbb K}
\newcommand{\bbL}{\mathbb L}
\newcommand{\bbM}{\mathbb M}
\newcommand{\bbN}{\mathbb N}
\newcommand{\bbO}{\mathbb O}
\newcommand{\bbP}{\mathbb P}
\newcommand{\bbQ}{\mathbb Q}
\newcommand{\bbR}{\mathbb R}
\newcommand{\bbS}{\mathbb S}
\newcommand{\bbT}{\mathbb T}
\newcommand{\bbU}{\mathbb U}
\newcommand{\bbV}{\mathbb V}
\newcommand{\bbW}{\mathbb W}
\newcommand{\bbX}{\mathbb X}
\newcommand{\bbY}{\mathbb Y}
\newcommand{\bbZ}{\mathbb Z}
\newcommand{\sA}{\mathscr A}
\newcommand{\sB}{\mathscr B}
\newcommand{\sC}{\mathscr C}
\newcommand{\sD}{\mathscr D}
\newcommand{\sE}{\mathscr E}
\newcommand{\sF}{\mathscr F}
\newcommand{\sG}{\mathscr G}
\newcommand{\sH}{\mathscr H}
\newcommand{\sI}{\mathscr I}
\newcommand{\sJ}{\mathscr J}
\newcommand{\sK}{\mathscr K}
\newcommand{\sL}{\mathscr L}
\newcommand{\sM}{\mathscr M}
\newcommand{\sN}{\mathscr N}
\newcommand{\sO}{\mathscr O}
\newcommand{\sP}{\mathscr P}
\newcommand{\sQ}{\mathscr Q}
\newcommand{\sR}{\mathscr R}
\newcommand{\sS}{\mathscr S}
\newcommand{\sT}{\mathscr T}
\newcommand{\sU}{\mathscr U}
\newcommand{\sV}{\mathscr V}
\newcommand{\sW}{\mathscr W}
\newcommand{\sX}{\mathscr X}
\newcommand{\sY}{\mathscr Y}
\newcommand{\sZ}{\mathscr Z}
\newcommand{\sfA}{\mathsf A}
\newcommand{\sfB}{\mathsf B}
\newcommand{\sfC}{\mathsf C}
\newcommand{\sfD}{\mathsf D}
\newcommand{\sfE}{\mathsf E}
\newcommand{\sfF}{\mathsf F}
\newcommand{\sfG}{\mathsf G}
\newcommand{\sfH}{\mathsf H}
\newcommand{\sfI}{\mathsf I}
\newcommand{\sfJ}{\mathsf J}
\newcommand{\sfK}{\mathsf K}
\newcommand{\sfL}{\mathsf L}
\newcommand{\sfM}{\mathsf M}
\newcommand{\sfN}{\mathsf N}
\newcommand{\sfO}{\mathsf O}
\newcommand{\sfP}{\mathsf P}
\newcommand{\sfQ}{\mathsf Q}
\newcommand{\sfR}{\mathsf R}
\newcommand{\sfS}{\mathsf S}
\newcommand{\sfT}{\mathsf T}
\newcommand{\sfU}{\mathsf U}
\newcommand{\sfV}{\mathsf V}
\newcommand{\sfW}{\mathsf W}
\newcommand{\sfX}{\mathsf X}
\newcommand{\sfY}{\mathsf Y}
\newcommand{\sfZ}{\mathsf Z}
\newcommand{\cA}{\mathcal A}
\newcommand{\cB}{\mathcal B}
\newcommand{\cC}{\mathcal C}
\newcommand{\cD}{\mathcal D}
\newcommand{\cE}{\mathcal E}
\newcommand{\cF}{\mathcal F}
\newcommand{\cG}{\mathcal G}
\newcommand{\cH}{\mathcal H}
\newcommand{\cI}{\mathcal I}
\newcommand{\cJ}{\mathcal J}
\newcommand{\cK}{\mathcal K}
\newcommand{\cL}{\mathcal L}
\newcommand{\cM}{\mathcal M}
\newcommand{\cN}{\mathcal N}
\newcommand{\cO}{\mathcal O}
\newcommand{\cP}{\mathcal P}
\newcommand{\cQ}{\mathcal Q}
\newcommand{\cR}{\mathcal R}
\newcommand{\cS}{\mathcal S}
\newcommand{\cT}{\mathcal T}
\newcommand{\cU}{\mathcal U}
\newcommand{\cV}{\mathcal V}
\newcommand{\cW}{\mathcal W}
\newcommand{\cX}{\mathcal X}
\newcommand{\cY}{\mathcal Y}
\newcommand{\cZ}{\mathcal Z}
\newcommand{\bfA}{\mathbf A}
\newcommand{\bfB}{\mathbf B}
\newcommand{\bfC}{\mathbf C}
\newcommand{\bfD}{\mathbf D}
\newcommand{\bfE}{\mathbf E}
\newcommand{\bfF}{\mathbf F}
\newcommand{\bfG}{\mathbf G}
\newcommand{\bfH}{\mathbf H}
\newcommand{\bfI}{\mathbf I}
\newcommand{\bfJ}{\mathbf J}
\newcommand{\bfK}{\mathbf K}
\newcommand{\bfL}{\mathbf L}
\newcommand{\bfM}{\mathbf M}
\newcommand{\bfN}{\mathbf N}
\newcommand{\bfO}{\mathbf O}
\newcommand{\bfP}{\mathbf P}
\newcommand{\bfQ}{\mathbf Q}
\newcommand{\bfR}{\mathbf R}
\newcommand{\bfS}{\mathbf S}
\newcommand{\bfT}{\mathbf T}
\newcommand{\bfU}{\mathbf U}
\newcommand{\bfV}{\mathbf V}
\newcommand{\bfW}{\mathbf W}
\newcommand{\bfX}{\mathbf X}
\newcommand{\bfY}{\mathbf Y}
\newcommand{\bfZ}{\mathbf Z}
\newcommand{\rmA}{\mathrm A}
\newcommand{\rmB}{\mathrm B}
\newcommand{\rmC}{\mathrm C}
\newcommand{\rmD}{\mathrm D}
\newcommand{\rmE}{\mathrm E}
\newcommand{\rmF}{\mathrm F}
\newcommand{\rmG}{\mathrm G}
\newcommand{\rmH}{\mathrm H}
\newcommand{\rmI}{\mathrm I}
\newcommand{\rmJ}{\mathrm J}
\newcommand{\rmK}{\mathrm K}
\newcommand{\rmL}{\mathrm L}
\newcommand{\rmM}{\mathrm M}
\newcommand{\rmN}{\mathrm N}
\newcommand{\rmO}{\mathrm O}
\newcommand{\rmP}{\mathrm P}
\newcommand{\rmQ}{\mathrm Q}
\newcommand{\rmR}{\mathrm R}
\newcommand{\rmS}{\mathrm S}
\newcommand{\rmT}{\mathrm T}
\newcommand{\rmU}{\mathrm U}
\newcommand{\rmV}{\mathrm V}
\newcommand{\rmW}{\mathrm W}
\newcommand{\rmX}{\mathrm X}
\newcommand{\rmY}{\mathrm Y}
\newcommand{\rmZ}{\mathrm Z}
\newcommand{\bb}{\mathbf{b}}
\newcommand{\bv}{\mathbf{v}}
\newcommand{\bw}{\mathbf{w}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\paren}[1]{( #1 )}
\newcommand{\Paren}[1]{\left( #1 \right)}
\newcommand{\bigparen}[1]{\bigl( #1 \bigr)}
\newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)}
\newcommand{\biggparen}[1]{\biggl( #1 \biggr)}
\newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)}
\newcommand{\abs}[1]{\lvert #1 \rvert}
\newcommand{\Abs}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\card}[1]{\left| #1 \right|}
\newcommand{\Card}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\norm}[1]{\lVert #1 \rVert}
\newcommand{\Norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert}
\newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert}
\newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert}
\newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\Iprod}[1]{\left\langle #1 \right\rangle}
\newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle}
\newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle}
\newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle}
\newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle}
\newcommand{\set}[1]{\lbrace #1 \rbrace}
\newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace}
\newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace}
\newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace}
\newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace}
\newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace}
\newcommand{\bracket}[1]{\lbrack #1 \rbrack}
\newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack}
\newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack}
\newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack}
\newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack}
\newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack}
\newcommand{\ucorner}[1]{\ulcorner #1 \urcorner}
\newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner}
\newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner}
\newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner}
\newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner}
\newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner}
\newcommand{\ceil}[1]{\lceil #1 \rceil}
\newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil}
\newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil}
\newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil}
\newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil}
\newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil}
\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor}
\newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor}
\newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor}
\newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor}
\newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor}
\newcommand{\lcorner}[1]{\llcorner #1 \lrcorner}
\newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner}
\newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner}
\newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner}
\newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner}
\newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner}
\newcommand{\ket}[1]{| #1 \rangle}
\newcommand{\bra}[1]{\langle #1 |}
\newcommand{\braket}[2]{\langle #1 | #2 \rangle}
\newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |}
\newcommand{\e}{\varepsilon}
\newcommand{\eps}{\varepsilon}
\newcommand{\from}{\colon}
\newcommand{\super}[2]{#1^{(#2)}}
\newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}}
\newcommand{\tensor}{\otimes}
\newcommand{\eset}{\emptyset}
\newcommand{\sse}{\subseteq}
\newcommand{\sst}{\substack}
\newcommand{\ot}{\otimes}
\newcommand{\Esst}[1]{\bbE_{\substack{#1}}}
\newcommand{\vbig}{\vphantom{\bigoplus}}
\newcommand{\seteq}{\mathrel{\mathop:}=}
\newcommand{\defeq}{\stackrel{\mathrm{def}}=}
\newcommand{\Mid}{\mathrel{}\middle|\mathrel{}}
\newcommand{\Ind}{\mathbf 1}
\newcommand{\bits}{\{0,1\}}
\newcommand{\sbits}{\{\pm 1\}}
\newcommand{\R}{\mathbb R}
\newcommand{\Rnn}{\R_{\ge 0}}
\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\C}{\mathbb C}
\newcommand{\A}{\mathbb A}
\newcommand{\Real}{\mathbb R}
\newcommand{\mper}{\,.}
\newcommand{\mcom}{\,,}
\DeclareMathOperator{\Id}{Id}
\DeclareMathOperator{\cone}{cone}
\DeclareMathOperator{\vol}{vol}
\DeclareMathOperator{\val}{val}
\DeclareMathOperator{\opt}{opt}
\DeclareMathOperator{\Opt}{Opt}
\DeclareMathOperator{\Val}{Val}
\DeclareMathOperator{\LP}{LP}
\DeclareMathOperator{\SDP}{SDP}
\DeclareMathOperator{\Tr}{Tr}
\DeclareMathOperator{\Inf}{Inf}
\DeclareMathOperator{\size}{size}
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\min}{min}
\DeclareMathOperator{\max}{max}
\DeclareMathOperator{\argmax}{arg\,max}
\DeclareMathOperator{\argmin}{arg\,min}
\DeclareMathOperator{\qpoly}{qpoly}
\DeclareMathOperator{\qqpoly}{qqpoly}
\DeclareMathOperator{\conv}{conv}
\DeclareMathOperator{\Conv}{Conv}
\DeclareMathOperator{\supp}{supp}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\perm}{perm}
\DeclareMathOperator{\mspan}{span}
\DeclareMathOperator{\mrank}{rank}
\DeclareMathOperator{\E}{\mathbb E}
\DeclareMathOperator{\pE}{\tilde{\mathbb E}}
\DeclareMathOperator{\Pr}{\mathbb P}
\DeclareMathOperator{\Span}{Span}
\DeclareMathOperator{\Cone}{Cone}
\DeclareMathOperator{\junta}{junta}
\DeclareMathOperator{\NSS}{NSS}
\DeclareMathOperator{\SA}{SA}
\DeclareMathOperator{\SOS}{SOS}
\DeclareMathOperator{\Stab}{\mathbf Stab}
\DeclareMathOperator{\Det}{\textbf{Det}}
\DeclareMathOperator{\Perm}{\textbf{Perm}}
\DeclareMathOperator{\Sym}{\textbf{Sym}}
\DeclareMathOperator{\Pow}{\textbf{Pow}}
\DeclareMathOperator{\Gal}{\textbf{Gal}}
\DeclareMathOperator{\Aut}{\textbf{Aut}}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\cE}{\mathcal{E}}
\newcommand{\E}{\mathbb{E}}
\newcommand{\pE}{\tilde{\mathbb{E}}}
\newcommand{\N}{\mathbb{N}}
\renewcommand{\P}{\mathcal{P}}
\notag
$
$
\newcommand{\sleq}{\ensuremath{\preceq}}
\newcommand{\sgeq}{\ensuremath{\succeq}}
\newcommand{\diag}{\ensuremath{\mathrm{diag}}}
\newcommand{\support}{\ensuremath{\mathrm{support}}}
\newcommand{\zo}{\ensuremath{\{0,1\}}}
\newcommand{\pmo}{\ensuremath{\{\pm 1\}}}
\newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}}
\newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}}
\newcommand{\rank}{\ensuremath{\mathrm{rank}}}
\newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}}
\newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}}
\newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}}
\newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}}
\newcommand{\eqdef}{\ensuremath{ =^{def}}}
\newcommand{\threshold}{\ensuremath{\mathrm{threshold}}}
\newcommand{\vbls}{\ensuremath{\mathrm{vbls}}}
\newcommand{\cons}{\ensuremath{\mathrm{cons}}}
\newcommand{\edges}{\ensuremath{\mathrm{edges}}}
\newcommand{\cl}{\ensuremath{\mathrm{cl}}}
\newcommand{\xor}{\ensuremath{\oplus}}
\newcommand{\1}{\ensuremath{\mathrm{1}}}
\notag
$
$
\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}}
\newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}}
\newcommand{\nchoose}[1]{\ensuremath}
\newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}}
\notag
$
$
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}
\newcommand{\R} % real numbers
\newcommand{\N}} % natural numbers
\newcommand{\Z} % integers
\newcommand{\F} % a field
\newcommand{\Q} % the rationals
\newcommand{\C}{\mathbb{C}} % the complexes
\newcommand{\poly}}
\newcommand{\polylog}}
\newcommand{\loglog}}}
\newcommand{\zo}{\{0,1\}}
\newcommand{\suchthat}
\newcommand{\pr}[1]{\Pr\left[#1\right]}
\newcommand{\deffont}{\em}
\newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}
\newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation
\newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance
\newcommand{\xor}{\oplus}
\newcommand{\GF}{\mathrm{GF}}
\newcommand{\eps}{\varepsilon}
\notag
$
$
\newcommand{\class}[1]{\mathbf{#1}}
\newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements
\newcommand{\BPP}{\class{BPP}}
\newcommand{\NP}{\class{NP}}
\newcommand{\RP}{\class{RP}}
\newcommand{\coRP}{\coclass{RP}}
\newcommand{\ZPP}{\class{ZPP}}
\newcommand{\BQP}{\class{BQP}}
\newcommand{\FP}{\class{FP}}
\newcommand{\QP}{\class{QuasiP}}
\newcommand{\VF}{\class{VF}}
\newcommand{\VBP}{\class{VBP}}
\newcommand{\VP}{\class{VP}}
\newcommand{\VNP}{\class{VNP}}
\newcommand{\RNC}{\class{RNC}}
\newcommand{\RL}{\class{RL}}
\newcommand{\BPL}{\class{BPL}}
\newcommand{\coRL}{\coclass{RL}}
\newcommand{\IP}{\class{IP}}
\newcommand{\AM}{\class{AM}}
\newcommand{\MA}{\class{MA}}
\newcommand{\QMA}{\class{QMA}}
\newcommand{\SBP}{\class{SBP}}
\newcommand{\coAM}{\class{coAM}}
\newcommand{\coMA}{\class{coMA}}
\renewcommand{\P}{\class{P}}
\newcommand\prBPP{\class{prBPP}}
\newcommand\prRP{\class{prRP}}
\newcommand\prP{\class{prP}}
\newcommand{\Ppoly}{\class{P/poly}}
\newcommand{\NPpoly}{\class{NP/poly}}
\newcommand{\coNPpoly}{\class{coNP/poly}}
\newcommand{\DTIME}{\class{DTIME}}
\newcommand{\TIME}{\class{TIME}}
\newcommand{\SIZE}{\class{SIZE}}
\newcommand{\SPACE}{\class{SPACE}}
\newcommand{\ETIME}{\class{E}}
\newcommand{\BPTIME}{\class{BPTIME}}
\newcommand{\RPTIME}{\class{RPTIME}}
\newcommand{\ZPTIME}{\class{ZPTIME}}
\newcommand{\EXP}{\class{EXP}}
\newcommand{\ZPEXP}{\class{ZPEXP}}
\newcommand{\RPEXP}{\class{RPEXP}}
\newcommand{\BPEXP}{\class{BPEXP}}
\newcommand{\SUBEXP}{\class{SUBEXP}}
\newcommand{\NTIME}{\class{NTIME}}
\newcommand{\NL}{\class{NL}}
\renewcommand{\L}{\class{L}}
\newcommand{\NQP}{\class{NQP}}
\newcommand{\NEXP}{\class{NEXP}}
\newcommand{\coNEXP}{\coclass{NEXP}}
\newcommand{\NPSPACE}{\class{NPSPACE}}
\newcommand{\PSPACE}{\class{PSPACE}}
\newcommand{\NSPACE}{\class{NSPACE}}
\newcommand{\coNSPACE}{\coclass{NSPACE}}
\newcommand{\coL}{\coclass{L}}
\newcommand{\coP}{\coclass{P}}
\newcommand{\coNP}{\coclass{NP}}
\newcommand{\coNL}{\coclass{NL}}
\newcommand{\coNPSPACE}{\coclass{NPSPACE}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\LINSPACE}{\class{LINSPACE}}
\newcommand{\qP}{\class{\tilde{P}}}
\newcommand{\PH}{\class{PH}}
\newcommand{\EXPSPACE}{\class{EXPSPACE}}
\newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}}
\newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}}
\newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}}
\newcommand{\PiP}[1]{\class{\Pi_{#1}P}}
\newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}}
\newcommand{\ATIME}{\class{ATIME}}
\newcommand{\ASPACE}{\class{ASPACE}}
\newcommand{\AP}{\class{AP}}
\newcommand{\AL}{\class{AL}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\VNC}[1]{\class{VNC^{#1}}}
\newcommand{\NC}[1]{\class{NC^{#1}}}
\newcommand{\AC}[1]{\class{AC^{#1}}}
\newcommand{\ACC}[1]{\class{ACC^{#1}}}
\newcommand{\TC}[1]{\class{TC^{#1}}}
\newcommand{\ShP}{\class{\# P}}
\newcommand{\PaP}{\class{\oplus P}}
\newcommand{\PCP}{\class{PCP}}
\newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}}
\newcommand{\MIP}{\class{MIP}}
$
$
\newcommand{\textprob}[1]{\text{#1}}
\newcommand{\mathprob}[1]{\textbf{#1}}
\newcommand{\Satisfiability}{\textprob{Satisfiability}}
\newcommand{\SAT}{\textprob{SAT}}
\newcommand{\TSAT}{\textprob{3SAT}}
\newcommand{\USAT}{\textprob{USAT}}
\newcommand{\UNSAT}{\textprob{UNSAT}}
\newcommand{\QPSAT}{\textprob{QPSAT}}
\newcommand{\TQBF}{\textprob{TQBF}}
\newcommand{\LinProg}{\textprob{Linear Programming}}
\newcommand{\LP}{\mathprob{LP}}
\newcommand{\Factor}{\textprob{Factoring}}
\newcommand{\CircVal}{\textprob{Circuit Value}}
\newcommand{\CVAL}{\mathprob{CVAL}}
\newcommand{\CircSat}{\textprob{Circuit Satisfiability}}
\newcommand{\CSAT}{\textprob{CSAT}}
\newcommand{\CycleCovers}{\textprob{Cycle Covers}}
\newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}}
\newcommand{\Reachability}{\textprob{Reachability}}
\newcommand{\Unreachability}{\textprob{Unreachability}}
\newcommand{\RCH}{\mathprob{RCH}}
\newcommand{\BddHalt}{\textprob{Bounded Halting}}
\newcommand{\BH}{\mathprob{BH}}
\newcommand{\DiscreteLog}{\textprob{Discrete Log}}
\newcommand{\REE}{\mathprob{REE}}
\newcommand{\QBF}{\mathprob{QBF}}
\newcommand{\MCSP}{\mathprob{MCSP}}
\newcommand{\GGEO}{\mathprob{GGEO}}
\newcommand{\CKTMIN}{\mathprob{CKT-MIN}}
\newcommand{\MINCKT}{\mathprob{MIN-CKT}}
\newcommand{\IdentityTest}{\textprob{Identity Testing}}
\newcommand{\Majority}{\textprob{Majority}}
\newcommand{\CountIndSets}{\textprob{\#Independent Sets}}
\newcommand{\Parity}{\textprob{Parity}}
\newcommand{\Clique}{\textprob{Clique}}
\newcommand{\CountCycles}{\textprob{#Cycles}}
\newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}}
\newcommand{\CountMatchings}{\textprob{\#Matchings}}
\newcommand{\CountMatch}{\mathprob{\#Matchings}}
\newcommand{\ECSAT}{\mathprob{E#SAT}}
\newcommand{\ShSAT}{\mathprob{#SAT}}
\newcommand{\ShTSAT}{\mathprob{#3SAT}}
\newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}}
\newcommand{\Permanent}{\textprob{Permanent}}
\newcommand{\ModPermanent}{\textprob{Modular Permanent}}
\newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}}
\newcommand{\GI}{\mathprob{GI}}
\newcommand{\GNI}{\mathprob{GNI}}
\newcommand{\GraphIso}{\textprob{Graph Isomorphism}}
\newcommand{\QuantBoolForm}{\textprob{Quantified Boolean
Formulae}}
\newcommand{\GenGeography}{\textprob{Generalized Geography}}
\newcommand{\MAXTSAT}{\mathprob{Max3SAT}}
\newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}}
\newcommand{\ELIN}{\mathprob{E3LIN2}}
\newcommand{\CSP}{\mathprob{CSP}}
\newcommand{\Lin}{\mathprob{Lin}}
\newcommand{\ONE}{\mathbf{ONE}}
\newcommand{\ZERO}{\mathbf{ZERO}}
\newcommand{\yes}
\newcommand{\no}
$
Parity is not in $\AC{0}$
Overview
In 1984, Furst, Saxe, and Sipser showed that the parity function does not lie in $\AC{0}$. Later on in 1986, Hastad showed an substantial improvement in his Ph.D. thesis.
We are going to prove the following theorem in several ways and discuss the implication as well as influence of this theorem.
For sufficiently large $n$ and any constant $d\geq2$, the parity function on $n$ bits cannot be computed by depth $d$ size $2^{n^{o(1/d)}}$ circuits with NOT gates, and unbounded fan-in AND, OR gates.
Parity is not in $\AC{0}$.
In fact, the above theorem can be much strengthened due to Hastad as follows.
For sufficiently large $n$ and any constant $d\geq2$, the parity function on $n$ bits cannot be computed by depth $d$ size $2^{n^{1/(d-1))}}$ circuits with NOT gates, and unbounded fan-in AND, OR gates.
Random restriction and switching lemma
The idea of random restriction is to randomly choose some input bits of a circuit and fix them to some random values. The hope is that after such random restriction, the circuit will becomes something simpler and easier to analyze. For example, in Hastad’s switching lemma, which we will see in a minute, after hitting a random restriction to a DNF or CNF, the resulting (restricted) function turns out to have a small decision tree with high probability.
In the rest of this section, we first formally define the mathematical formulation of random restriction. Then give an overview/review on decision tree, DNF, and CNF. Finally, we state and prove Hastad’s switching lemma and use it to complete the proof for our main theorem showing parity function not in $\AC{0}$.
Random restriction
As a disclaimer, there are many different forms of random restrictions on different circuit models. Here we focus on one of the simplest and basic one. In particular, all the randomness here are chosen uniformly over the domain while in some applications beyond the scope of this notes people might consider biased random restriction.
Let $f:{0,1}^n\rightarrow{0,1}$ be an $n$-bit boolean function. For every integer $1\leq m\leq n$, a random $m$-restriction can be sampled as follows.
- Randomly choose a subset $S\subseteq[n]$ of size $\card{S}=n-m$.
- Randomly choose a string in $v\in{0,1}^{n-m}$.
- Set the variables chosen by $S$ to value $v$.
We denote a restriction as $\rho$ and denote the resulting restricted function as $f\vert_\rho$. Note that if $\rho$ is a $m$-restriction then $f\vert_\rho$ is an $m$-bit function.
Decision tree, DNF, and CNF
Decision tree (DT) is one of the simplest and natural computational models. For boolean function, a decision tree is simply a binary tree with internal vertices associated by a variable $x_i$ and the two out-going edges correspond to $x_i$ being set to $0$ or $1$. The leaves of a decision tree are indexed by $0$ or $1$. The boolean function computed by a decision tree $T$ is naturally defined as starting from the root and going downward according to the value of to variables and finally outputting the value in the leaf one ends at. See the following for an example.
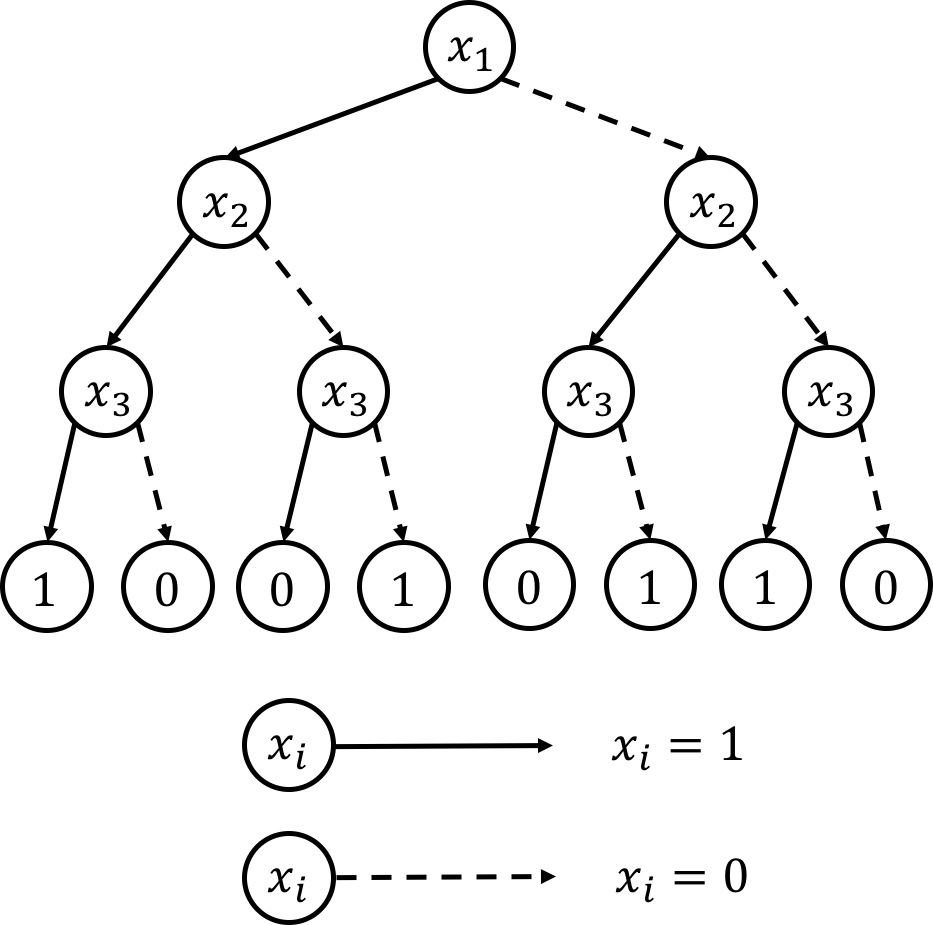
In decision tree, we are usually interested in the depth (i.e., the longest distance from the root to a leaf) of the tree as an important complexity measure. It is not difficult to see that any decision tree that computes the parity function of $n$ bits requires depth to be at least $n$.
A CNF (Conjunctive Normal Form) is of the form $C_1\wedge\cdots\wedge C_s$ where each $C_i=(\ell_{i_1}\vee\cdots\vee\ell_{i_w})$, $\ell_{i_j}$ is a literal (i.e., of the form $x$ or $\neg x$ for some variable $x$), and $w$ is called the width of this CNF. Similarly, a DNF (Disjunctive Normal Form) is of the form $C_1\vee\cdots\vee C_s$ where each $C_i=(\ell_{i_1}\wedge\cdots\wedge\ell_{i_w})$. The important complexity measures of CNF and DNF are the size (i.e., the number of clauses) and the width.
Some basic but important observations about decision tree, CNF, and DNF:
- Every decision tree of depth $d$ can be turned into a CNF (also DNF) of width at most $d$ and size at most $2^d$. Can you see how?
- Every CNF (also DNF) of width $w$ and size $s$ can be turned into a decision tree of depth at most $w$. In particular, one can turn it into a canonical decision tree that has special structure as depicted in the following figure.
[TODO: add a figure]
Hastad’s switching lemma
In 1986, Hastad proved the following switching lemma.
Let $f:\bit^n\rightarrow\bit$ be a function that can be expressed by a DNF or CNF of width at most $w$. Let $1\leq m\leq n/5$ and let $\rho$ be a random $m$-restriction. Then, for any $d\geq2$,
\begin{equation}
\mathbb{P}_{\rho}[f\vert_{\rho} \text{ is not expressible as a }\text{DT of depth }d]\leq\left(\frac{mw}{n}\right)^{d}.
\end{equation}
[TODO: complete the proof]
Now, we show how to use switching lemma to prove our main theorem. The overall strategy is to use a sequence of random restrictions $\rho_0,\rho_1,\dots,\rho_{d-2}$ with properly chosen size and show that for every $AC{0}$ circuit $C$ of size $s$ and depth $d$,
\begin{equation}
\Pr_{\rho_0,\dots,\rho_{d-2}}[C\vert_{\rho_0}\cdots \vert_{\rho_{d-2}}\text{ is not expressible as a }\text{DT of depth }m]<1
\end{equation}
where $m$ is the number of free variables left after the restrictions $\rho_0,\rho_1,\dots,\rho_{d-2}$.
Step 1: Turn a circuit into the general position
Let’s fix an arbitrary $AC{0}$ circuit $C$ of size $s$ and depth $d$. We turn $C$ into the general position described as follows.
- The fan-out of every gates is 1 so that $C$ is a tree.
- All the NOT gates lie in first layer of $C$.
- The AND and OR gates are switching between layers.
- The input/bottom layer consists of OR gates with fan-in at most $10\log s$.
Note that for the first three bullets, we can them with at most polynomial blow-up in size and no blow-up in depth. For the last bullet, in general we cannot do so. The trick is that we first apply a random $(n/2)$-restriction $\rho_0$ so that with probability at least $1-0.1$ each bottom OR gate with fan-in more than $10\log s$ is fixed by the restriction.
Step 2: Reduce the depth by random restriction
In this step, we use switching lemma together with union bound and probabilistic method to reduce the depth of the circuit. Concretely, we want to inductively show the following: After the $i$th iteration for $i=1,\dots d-1$.
- The circuit has depth $d-i$.
- The gates in the bottom layer have fan-in at most $k_i$ where $k_i$ is a constant set later.
- The gates in the layer above the bottom layer can be expressed with a
- There are $n_i-\sqrt{n_i}$ inputs being fixed and $\sqrt{n_i}$ left undetermined where $n_0=n$ and $n_i=n^{1/2^{i}}$.
We achieve the above setting by the following probabilistic argument.
- By induction, we know that at the beginning of the $i$th iteration, the gates in the layer above the bottom layer can be expressed as a $(k_{i-1})$-CNF (or $(k_{i-1})$-DNF). Thus, we can apply Hastad’s switching lemma.
- For a single gate in the layer above the bottom layer, the probability of cannot be expressed as a $k_i$-DNF (or $k_i$-CNF) is at most
\begin{equation}
(\frac{\sqrt{n_i}k_{i-1}^{10}}{n_i})^{k_i/2}.
\end{equation}
Take $k_i=10b2^{i+2}$, the probability is upper bounded by $1/(10n^{n^b})$. As a result, by union bound and probabilistic argument, we know that there exists a restriction of size $n_i-\sqrt{n_i}$ such that every gates in the layer above the bottom layer can be expressed as a $k_i$-DNF (or $k_i$-DNF). As a result, we can combine the layer above the bottom layer with the layer above into a single layer.
Step 3: Final step
After $d-2$ iteration, the circuit has the following properties.
- Having $n_{d-2}=n^{1/2^{d-2}}$ input bits remain unfixed.
- The circuit can be expressed as a $k_{d-2}$-CNF (or $k_{d-2}$-DNF).
As a result, the output of the circuit can be determined by $k_{d-2}$ value which is a constant with respect to the remaining unfixed input bits. As the parity function cannot be determined until the last bit is fixed, we know that $C$ cannot compute the parity function.
Polynomial approximation
Fourier analysis and learning
