$
\newcommand{\undefined}{}
\newcommand{\hfill}{}
\newcommand{\qedhere}{\square}
\newcommand{\qed}{\square}
\newcommand{\ensuremath}[1]{#1}
\newcommand{\bit}{\{0,1\}}
\newcommand{\Bit}{\{-1,1\}}
\newcommand{\Stab}{\mathbf{Stab}}
\newcommand{\NS}{\mathbf{NS}}
\newcommand{\ba}{\mathbf{a}}
\newcommand{\bc}{\mathbf{c}}
\newcommand{\bd}{\mathbf{d}}
\newcommand{\be}{\mathbf{e}}
\newcommand{\bh}{\mathbf{h}}
\newcommand{\br}{\mathbf{r}}
\newcommand{\bs}{\mathbf{s}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\Var}{\mathbf{Var}}
\newcommand{\dist}{\text{dist}}
\newcommand{\norm}[1]{\\|#1\\|}
\newcommand{\etal}
\newcommand{\ie}
\newcommand{\eg}
\newcommand{\cf}
\newcommand{\rank}{\text{rank}}
\newcommand{\tr}{\text{tr}}
\newcommand{\mor}{\text{Mor}}
\newcommand{\hom}{\text{Hom}}
\newcommand{\id}{\text{id}}
\newcommand{\obj}{\text{obj}}
\newcommand{\pr}{\text{pr}}
\newcommand{\ker}{\text{ker}}
\newcommand{\coker}{\text{coker}}
\newcommand{\im}{\text{im}}
\newcommand{\vol}{\text{vol}}
\newcommand{\disc}{\text{disc}}
\newcommand{\bbA}{\mathbb A}
\newcommand{\bbB}{\mathbb B}
\newcommand{\bbC}{\mathbb C}
\newcommand{\bbD}{\mathbb D}
\newcommand{\bbE}{\mathbb E}
\newcommand{\bbF}{\mathbb F}
\newcommand{\bbG}{\mathbb G}
\newcommand{\bbH}{\mathbb H}
\newcommand{\bbI}{\mathbb I}
\newcommand{\bbJ}{\mathbb J}
\newcommand{\bbK}{\mathbb K}
\newcommand{\bbL}{\mathbb L}
\newcommand{\bbM}{\mathbb M}
\newcommand{\bbN}{\mathbb N}
\newcommand{\bbO}{\mathbb O}
\newcommand{\bbP}{\mathbb P}
\newcommand{\bbQ}{\mathbb Q}
\newcommand{\bbR}{\mathbb R}
\newcommand{\bbS}{\mathbb S}
\newcommand{\bbT}{\mathbb T}
\newcommand{\bbU}{\mathbb U}
\newcommand{\bbV}{\mathbb V}
\newcommand{\bbW}{\mathbb W}
\newcommand{\bbX}{\mathbb X}
\newcommand{\bbY}{\mathbb Y}
\newcommand{\bbZ}{\mathbb Z}
\newcommand{\sA}{\mathscr A}
\newcommand{\sB}{\mathscr B}
\newcommand{\sC}{\mathscr C}
\newcommand{\sD}{\mathscr D}
\newcommand{\sE}{\mathscr E}
\newcommand{\sF}{\mathscr F}
\newcommand{\sG}{\mathscr G}
\newcommand{\sH}{\mathscr H}
\newcommand{\sI}{\mathscr I}
\newcommand{\sJ}{\mathscr J}
\newcommand{\sK}{\mathscr K}
\newcommand{\sL}{\mathscr L}
\newcommand{\sM}{\mathscr M}
\newcommand{\sN}{\mathscr N}
\newcommand{\sO}{\mathscr O}
\newcommand{\sP}{\mathscr P}
\newcommand{\sQ}{\mathscr Q}
\newcommand{\sR}{\mathscr R}
\newcommand{\sS}{\mathscr S}
\newcommand{\sT}{\mathscr T}
\newcommand{\sU}{\mathscr U}
\newcommand{\sV}{\mathscr V}
\newcommand{\sW}{\mathscr W}
\newcommand{\sX}{\mathscr X}
\newcommand{\sY}{\mathscr Y}
\newcommand{\sZ}{\mathscr Z}
\newcommand{\sfA}{\mathsf A}
\newcommand{\sfB}{\mathsf B}
\newcommand{\sfC}{\mathsf C}
\newcommand{\sfD}{\mathsf D}
\newcommand{\sfE}{\mathsf E}
\newcommand{\sfF}{\mathsf F}
\newcommand{\sfG}{\mathsf G}
\newcommand{\sfH}{\mathsf H}
\newcommand{\sfI}{\mathsf I}
\newcommand{\sfJ}{\mathsf J}
\newcommand{\sfK}{\mathsf K}
\newcommand{\sfL}{\mathsf L}
\newcommand{\sfM}{\mathsf M}
\newcommand{\sfN}{\mathsf N}
\newcommand{\sfO}{\mathsf O}
\newcommand{\sfP}{\mathsf P}
\newcommand{\sfQ}{\mathsf Q}
\newcommand{\sfR}{\mathsf R}
\newcommand{\sfS}{\mathsf S}
\newcommand{\sfT}{\mathsf T}
\newcommand{\sfU}{\mathsf U}
\newcommand{\sfV}{\mathsf V}
\newcommand{\sfW}{\mathsf W}
\newcommand{\sfX}{\mathsf X}
\newcommand{\sfY}{\mathsf Y}
\newcommand{\sfZ}{\mathsf Z}
\newcommand{\cA}{\mathcal A}
\newcommand{\cB}{\mathcal B}
\newcommand{\cC}{\mathcal C}
\newcommand{\cD}{\mathcal D}
\newcommand{\cE}{\mathcal E}
\newcommand{\cF}{\mathcal F}
\newcommand{\cG}{\mathcal G}
\newcommand{\cH}{\mathcal H}
\newcommand{\cI}{\mathcal I}
\newcommand{\cJ}{\mathcal J}
\newcommand{\cK}{\mathcal K}
\newcommand{\cL}{\mathcal L}
\newcommand{\cM}{\mathcal M}
\newcommand{\cN}{\mathcal N}
\newcommand{\cO}{\mathcal O}
\newcommand{\cP}{\mathcal P}
\newcommand{\cQ}{\mathcal Q}
\newcommand{\cR}{\mathcal R}
\newcommand{\cS}{\mathcal S}
\newcommand{\cT}{\mathcal T}
\newcommand{\cU}{\mathcal U}
\newcommand{\cV}{\mathcal V}
\newcommand{\cW}{\mathcal W}
\newcommand{\cX}{\mathcal X}
\newcommand{\cY}{\mathcal Y}
\newcommand{\cZ}{\mathcal Z}
\newcommand{\bfA}{\mathbf A}
\newcommand{\bfB}{\mathbf B}
\newcommand{\bfC}{\mathbf C}
\newcommand{\bfD}{\mathbf D}
\newcommand{\bfE}{\mathbf E}
\newcommand{\bfF}{\mathbf F}
\newcommand{\bfG}{\mathbf G}
\newcommand{\bfH}{\mathbf H}
\newcommand{\bfI}{\mathbf I}
\newcommand{\bfJ}{\mathbf J}
\newcommand{\bfK}{\mathbf K}
\newcommand{\bfL}{\mathbf L}
\newcommand{\bfM}{\mathbf M}
\newcommand{\bfN}{\mathbf N}
\newcommand{\bfO}{\mathbf O}
\newcommand{\bfP}{\mathbf P}
\newcommand{\bfQ}{\mathbf Q}
\newcommand{\bfR}{\mathbf R}
\newcommand{\bfS}{\mathbf S}
\newcommand{\bfT}{\mathbf T}
\newcommand{\bfU}{\mathbf U}
\newcommand{\bfV}{\mathbf V}
\newcommand{\bfW}{\mathbf W}
\newcommand{\bfX}{\mathbf X}
\newcommand{\bfY}{\mathbf Y}
\newcommand{\bfZ}{\mathbf Z}
\newcommand{\rmA}{\mathrm A}
\newcommand{\rmB}{\mathrm B}
\newcommand{\rmC}{\mathrm C}
\newcommand{\rmD}{\mathrm D}
\newcommand{\rmE}{\mathrm E}
\newcommand{\rmF}{\mathrm F}
\newcommand{\rmG}{\mathrm G}
\newcommand{\rmH}{\mathrm H}
\newcommand{\rmI}{\mathrm I}
\newcommand{\rmJ}{\mathrm J}
\newcommand{\rmK}{\mathrm K}
\newcommand{\rmL}{\mathrm L}
\newcommand{\rmM}{\mathrm M}
\newcommand{\rmN}{\mathrm N}
\newcommand{\rmO}{\mathrm O}
\newcommand{\rmP}{\mathrm P}
\newcommand{\rmQ}{\mathrm Q}
\newcommand{\rmR}{\mathrm R}
\newcommand{\rmS}{\mathrm S}
\newcommand{\rmT}{\mathrm T}
\newcommand{\rmU}{\mathrm U}
\newcommand{\rmV}{\mathrm V}
\newcommand{\rmW}{\mathrm W}
\newcommand{\rmX}{\mathrm X}
\newcommand{\rmY}{\mathrm Y}
\newcommand{\rmZ}{\mathrm Z}
\newcommand{\bb}{\mathbf{b}}
\newcommand{\bv}{\mathbf{v}}
\newcommand{\bw}{\mathbf{w}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\paren}[1]{( #1 )}
\newcommand{\Paren}[1]{\left( #1 \right)}
\newcommand{\bigparen}[1]{\bigl( #1 \bigr)}
\newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)}
\newcommand{\biggparen}[1]{\biggl( #1 \biggr)}
\newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)}
\newcommand{\abs}[1]{\lvert #1 \rvert}
\newcommand{\Abs}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\card}[1]{\left| #1 \right|}
\newcommand{\Card}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\norm}[1]{\lVert #1 \rVert}
\newcommand{\Norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert}
\newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert}
\newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert}
\newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\Iprod}[1]{\left\langle #1 \right\rangle}
\newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle}
\newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle}
\newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle}
\newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle}
\newcommand{\set}[1]{\lbrace #1 \rbrace}
\newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace}
\newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace}
\newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace}
\newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace}
\newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace}
\newcommand{\bracket}[1]{\lbrack #1 \rbrack}
\newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack}
\newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack}
\newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack}
\newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack}
\newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack}
\newcommand{\ucorner}[1]{\ulcorner #1 \urcorner}
\newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner}
\newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner}
\newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner}
\newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner}
\newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner}
\newcommand{\ceil}[1]{\lceil #1 \rceil}
\newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil}
\newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil}
\newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil}
\newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil}
\newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil}
\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor}
\newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor}
\newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor}
\newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor}
\newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor}
\newcommand{\lcorner}[1]{\llcorner #1 \lrcorner}
\newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner}
\newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner}
\newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner}
\newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner}
\newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner}
\newcommand{\ket}[1]{| #1 \rangle}
\newcommand{\bra}[1]{\langle #1 |}
\newcommand{\braket}[2]{\langle #1 | #2 \rangle}
\newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |}
\newcommand{\e}{\varepsilon}
\newcommand{\eps}{\varepsilon}
\newcommand{\from}{\colon}
\newcommand{\super}[2]{#1^{(#2)}}
\newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}}
\newcommand{\tensor}{\otimes}
\newcommand{\eset}{\emptyset}
\newcommand{\sse}{\subseteq}
\newcommand{\sst}{\substack}
\newcommand{\ot}{\otimes}
\newcommand{\Esst}[1]{\bbE_{\substack{#1}}}
\newcommand{\vbig}{\vphantom{\bigoplus}}
\newcommand{\seteq}{\mathrel{\mathop:}=}
\newcommand{\defeq}{\stackrel{\mathrm{def}}=}
\newcommand{\Mid}{\mathrel{}\middle|\mathrel{}}
\newcommand{\Ind}{\mathbf 1}
\newcommand{\bits}{\{0,1\}}
\newcommand{\sbits}{\{\pm 1\}}
\newcommand{\R}{\mathbb R}
\newcommand{\Rnn}{\R_{\ge 0}}
\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\C}{\mathbb C}
\newcommand{\A}{\mathbb A}
\newcommand{\Real}{\mathbb R}
\newcommand{\mper}{\,.}
\newcommand{\mcom}{\,,}
\DeclareMathOperator{\Id}{Id}
\DeclareMathOperator{\cone}{cone}
\DeclareMathOperator{\vol}{vol}
\DeclareMathOperator{\val}{val}
\DeclareMathOperator{\opt}{opt}
\DeclareMathOperator{\Opt}{Opt}
\DeclareMathOperator{\Val}{Val}
\DeclareMathOperator{\LP}{LP}
\DeclareMathOperator{\SDP}{SDP}
\DeclareMathOperator{\Tr}{Tr}
\DeclareMathOperator{\Inf}{Inf}
\DeclareMathOperator{\size}{size}
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\min}{min}
\DeclareMathOperator{\max}{max}
\DeclareMathOperator{\argmax}{arg\,max}
\DeclareMathOperator{\argmin}{arg\,min}
\DeclareMathOperator{\qpoly}{qpoly}
\DeclareMathOperator{\qqpoly}{qqpoly}
\DeclareMathOperator{\conv}{conv}
\DeclareMathOperator{\Conv}{Conv}
\DeclareMathOperator{\supp}{supp}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\perm}{perm}
\DeclareMathOperator{\mspan}{span}
\DeclareMathOperator{\mrank}{rank}
\DeclareMathOperator{\E}{\mathbb E}
\DeclareMathOperator{\pE}{\tilde{\mathbb E}}
\DeclareMathOperator{\Pr}{\mathbb P}
\DeclareMathOperator{\Span}{Span}
\DeclareMathOperator{\Cone}{Cone}
\DeclareMathOperator{\junta}{junta}
\DeclareMathOperator{\NSS}{NSS}
\DeclareMathOperator{\SA}{SA}
\DeclareMathOperator{\SOS}{SOS}
\DeclareMathOperator{\Stab}{\mathbf Stab}
\DeclareMathOperator{\Det}{\textbf{Det}}
\DeclareMathOperator{\Perm}{\textbf{Perm}}
\DeclareMathOperator{\Sym}{\textbf{Sym}}
\DeclareMathOperator{\Pow}{\textbf{Pow}}
\DeclareMathOperator{\Gal}{\textbf{Gal}}
\DeclareMathOperator{\Aut}{\textbf{Aut}}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\cE}{\mathcal{E}}
\newcommand{\E}{\mathbb{E}}
\newcommand{\pE}{\tilde{\mathbb{E}}}
\newcommand{\N}{\mathbb{N}}
\renewcommand{\P}{\mathcal{P}}
\notag
$
$
\newcommand{\sleq}{\ensuremath{\preceq}}
\newcommand{\sgeq}{\ensuremath{\succeq}}
\newcommand{\diag}{\ensuremath{\mathrm{diag}}}
\newcommand{\support}{\ensuremath{\mathrm{support}}}
\newcommand{\zo}{\ensuremath{\{0,1\}}}
\newcommand{\pmo}{\ensuremath{\{\pm 1\}}}
\newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}}
\newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}}
\newcommand{\rank}{\ensuremath{\mathrm{rank}}}
\newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}}
\newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}}
\newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}}
\newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}}
\newcommand{\eqdef}{\ensuremath{ =^{def}}}
\newcommand{\threshold}{\ensuremath{\mathrm{threshold}}}
\newcommand{\vbls}{\ensuremath{\mathrm{vbls}}}
\newcommand{\cons}{\ensuremath{\mathrm{cons}}}
\newcommand{\edges}{\ensuremath{\mathrm{edges}}}
\newcommand{\cl}{\ensuremath{\mathrm{cl}}}
\newcommand{\xor}{\ensuremath{\oplus}}
\newcommand{\1}{\ensuremath{\mathrm{1}}}
\notag
$
$
\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}}
\newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}}
\newcommand{\nchoose}[1]{\ensuremath}
\newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}}
\notag
$
$
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}
\newcommand{\R} % real numbers
\newcommand{\N}} % natural numbers
\newcommand{\Z} % integers
\newcommand{\F} % a field
\newcommand{\Q} % the rationals
\newcommand{\C}{\mathbb{C}} % the complexes
\newcommand{\poly}}
\newcommand{\polylog}}
\newcommand{\loglog}}}
\newcommand{\zo}{\{0,1\}}
\newcommand{\suchthat}
\newcommand{\pr}[1]{\Pr\left[#1\right]}
\newcommand{\deffont}{\em}
\newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}
\newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation
\newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance
\newcommand{\xor}{\oplus}
\newcommand{\GF}{\mathrm{GF}}
\newcommand{\eps}{\varepsilon}
\notag
$
$
\newcommand{\class}[1]{\mathbf{#1}}
\newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements
\newcommand{\BPP}{\class{BPP}}
\newcommand{\NP}{\class{NP}}
\newcommand{\RP}{\class{RP}}
\newcommand{\coRP}{\coclass{RP}}
\newcommand{\ZPP}{\class{ZPP}}
\newcommand{\BQP}{\class{BQP}}
\newcommand{\FP}{\class{FP}}
\newcommand{\QP}{\class{QuasiP}}
\newcommand{\VF}{\class{VF}}
\newcommand{\VBP}{\class{VBP}}
\newcommand{\VP}{\class{VP}}
\newcommand{\VNP}{\class{VNP}}
\newcommand{\RNC}{\class{RNC}}
\newcommand{\RL}{\class{RL}}
\newcommand{\BPL}{\class{BPL}}
\newcommand{\coRL}{\coclass{RL}}
\newcommand{\IP}{\class{IP}}
\newcommand{\AM}{\class{AM}}
\newcommand{\MA}{\class{MA}}
\newcommand{\QMA}{\class{QMA}}
\newcommand{\SBP}{\class{SBP}}
\newcommand{\coAM}{\class{coAM}}
\newcommand{\coMA}{\class{coMA}}
\renewcommand{\P}{\class{P}}
\newcommand\prBPP{\class{prBPP}}
\newcommand\prRP{\class{prRP}}
\newcommand\prP{\class{prP}}
\newcommand{\Ppoly}{\class{P/poly}}
\newcommand{\NPpoly}{\class{NP/poly}}
\newcommand{\coNPpoly}{\class{coNP/poly}}
\newcommand{\DTIME}{\class{DTIME}}
\newcommand{\TIME}{\class{TIME}}
\newcommand{\SIZE}{\class{SIZE}}
\newcommand{\SPACE}{\class{SPACE}}
\newcommand{\ETIME}{\class{E}}
\newcommand{\BPTIME}{\class{BPTIME}}
\newcommand{\RPTIME}{\class{RPTIME}}
\newcommand{\ZPTIME}{\class{ZPTIME}}
\newcommand{\EXP}{\class{EXP}}
\newcommand{\ZPEXP}{\class{ZPEXP}}
\newcommand{\RPEXP}{\class{RPEXP}}
\newcommand{\BPEXP}{\class{BPEXP}}
\newcommand{\SUBEXP}{\class{SUBEXP}}
\newcommand{\NTIME}{\class{NTIME}}
\newcommand{\NL}{\class{NL}}
\renewcommand{\L}{\class{L}}
\newcommand{\NQP}{\class{NQP}}
\newcommand{\NEXP}{\class{NEXP}}
\newcommand{\coNEXP}{\coclass{NEXP}}
\newcommand{\NPSPACE}{\class{NPSPACE}}
\newcommand{\PSPACE}{\class{PSPACE}}
\newcommand{\NSPACE}{\class{NSPACE}}
\newcommand{\coNSPACE}{\coclass{NSPACE}}
\newcommand{\coL}{\coclass{L}}
\newcommand{\coP}{\coclass{P}}
\newcommand{\coNP}{\coclass{NP}}
\newcommand{\coNL}{\coclass{NL}}
\newcommand{\coNPSPACE}{\coclass{NPSPACE}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\LINSPACE}{\class{LINSPACE}}
\newcommand{\qP}{\class{\tilde{P}}}
\newcommand{\PH}{\class{PH}}
\newcommand{\EXPSPACE}{\class{EXPSPACE}}
\newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}}
\newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}}
\newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}}
\newcommand{\PiP}[1]{\class{\Pi_{#1}P}}
\newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}}
\newcommand{\ATIME}{\class{ATIME}}
\newcommand{\ASPACE}{\class{ASPACE}}
\newcommand{\AP}{\class{AP}}
\newcommand{\AL}{\class{AL}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\VNC}[1]{\class{VNC^{#1}}}
\newcommand{\NC}[1]{\class{NC^{#1}}}
\newcommand{\AC}[1]{\class{AC^{#1}}}
\newcommand{\ACC}[1]{\class{ACC^{#1}}}
\newcommand{\TC}[1]{\class{TC^{#1}}}
\newcommand{\ShP}{\class{\# P}}
\newcommand{\PaP}{\class{\oplus P}}
\newcommand{\PCP}{\class{PCP}}
\newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}}
\newcommand{\MIP}{\class{MIP}}
$
$
\newcommand{\textprob}[1]{\text{#1}}
\newcommand{\mathprob}[1]{\textbf{#1}}
\newcommand{\Satisfiability}{\textprob{Satisfiability}}
\newcommand{\SAT}{\textprob{SAT}}
\newcommand{\TSAT}{\textprob{3SAT}}
\newcommand{\USAT}{\textprob{USAT}}
\newcommand{\UNSAT}{\textprob{UNSAT}}
\newcommand{\QPSAT}{\textprob{QPSAT}}
\newcommand{\TQBF}{\textprob{TQBF}}
\newcommand{\LinProg}{\textprob{Linear Programming}}
\newcommand{\LP}{\mathprob{LP}}
\newcommand{\Factor}{\textprob{Factoring}}
\newcommand{\CircVal}{\textprob{Circuit Value}}
\newcommand{\CVAL}{\mathprob{CVAL}}
\newcommand{\CircSat}{\textprob{Circuit Satisfiability}}
\newcommand{\CSAT}{\textprob{CSAT}}
\newcommand{\CycleCovers}{\textprob{Cycle Covers}}
\newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}}
\newcommand{\Reachability}{\textprob{Reachability}}
\newcommand{\Unreachability}{\textprob{Unreachability}}
\newcommand{\RCH}{\mathprob{RCH}}
\newcommand{\BddHalt}{\textprob{Bounded Halting}}
\newcommand{\BH}{\mathprob{BH}}
\newcommand{\DiscreteLog}{\textprob{Discrete Log}}
\newcommand{\REE}{\mathprob{REE}}
\newcommand{\QBF}{\mathprob{QBF}}
\newcommand{\MCSP}{\mathprob{MCSP}}
\newcommand{\GGEO}{\mathprob{GGEO}}
\newcommand{\CKTMIN}{\mathprob{CKT-MIN}}
\newcommand{\MINCKT}{\mathprob{MIN-CKT}}
\newcommand{\IdentityTest}{\textprob{Identity Testing}}
\newcommand{\Majority}{\textprob{Majority}}
\newcommand{\CountIndSets}{\textprob{\#Independent Sets}}
\newcommand{\Parity}{\textprob{Parity}}
\newcommand{\Clique}{\textprob{Clique}}
\newcommand{\CountCycles}{\textprob{#Cycles}}
\newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}}
\newcommand{\CountMatchings}{\textprob{\#Matchings}}
\newcommand{\CountMatch}{\mathprob{\#Matchings}}
\newcommand{\ECSAT}{\mathprob{E#SAT}}
\newcommand{\ShSAT}{\mathprob{#SAT}}
\newcommand{\ShTSAT}{\mathprob{#3SAT}}
\newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}}
\newcommand{\Permanent}{\textprob{Permanent}}
\newcommand{\ModPermanent}{\textprob{Modular Permanent}}
\newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}}
\newcommand{\GI}{\mathprob{GI}}
\newcommand{\GNI}{\mathprob{GNI}}
\newcommand{\GraphIso}{\textprob{Graph Isomorphism}}
\newcommand{\QuantBoolForm}{\textprob{Quantified Boolean
Formulae}}
\newcommand{\GenGeography}{\textprob{Generalized Geography}}
\newcommand{\MAXTSAT}{\mathprob{Max3SAT}}
\newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}}
\newcommand{\ELIN}{\mathprob{E3LIN2}}
\newcommand{\CSP}{\mathprob{CSP}}
\newcommand{\Lin}{\mathprob{Lin}}
\newcommand{\ONE}{\mathbf{ONE}}
\newcommand{\ZERO}{\mathbf{ZERO}}
\newcommand{\yes}
\newcommand{\no}
$
$
\newcommand{\undefined}{}
\newcommand{\hfill}{}
\newcommand{\qedhere}{\square}
\newcommand{\qed}{\square}
\newcommand{\ensuremath}[1]{#1}
\newcommand{\bit}{\{0,1\}}
\newcommand{\Bit}{\{-1,1\}}
\newcommand{\Stab}{\mathbf{Stab}}
\newcommand{\NS}{\mathbf{NS}}
\newcommand{\ba}{\mathbf{a}}
\newcommand{\bc}{\mathbf{c}}
\newcommand{\bd}{\mathbf{d}}
\newcommand{\be}{\mathbf{e}}
\newcommand{\bh}{\mathbf{h}}
\newcommand{\br}{\mathbf{r}}
\newcommand{\bs}{\mathbf{s}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\Var}{\mathbf{Var}}
\newcommand{\dist}{\text{dist}}
\newcommand{\norm}[1]{\\|#1\\|}
\newcommand{\etal}
\newcommand{\ie}
\newcommand{\eg}
\newcommand{\cf}
\newcommand{\rank}{\text{rank}}
\newcommand{\tr}{\text{tr}}
\newcommand{\mor}{\text{Mor}}
\newcommand{\hom}{\text{Hom}}
\newcommand{\id}{\text{id}}
\newcommand{\obj}{\text{obj}}
\newcommand{\pr}{\text{pr}}
\newcommand{\ker}{\text{ker}}
\newcommand{\coker}{\text{coker}}
\newcommand{\im}{\text{im}}
\newcommand{\vol}{\text{vol}}
\newcommand{\disc}{\text{disc}}
\newcommand{\bbA}{\mathbb A}
\newcommand{\bbB}{\mathbb B}
\newcommand{\bbC}{\mathbb C}
\newcommand{\bbD}{\mathbb D}
\newcommand{\bbE}{\mathbb E}
\newcommand{\bbF}{\mathbb F}
\newcommand{\bbG}{\mathbb G}
\newcommand{\bbH}{\mathbb H}
\newcommand{\bbI}{\mathbb I}
\newcommand{\bbJ}{\mathbb J}
\newcommand{\bbK}{\mathbb K}
\newcommand{\bbL}{\mathbb L}
\newcommand{\bbM}{\mathbb M}
\newcommand{\bbN}{\mathbb N}
\newcommand{\bbO}{\mathbb O}
\newcommand{\bbP}{\mathbb P}
\newcommand{\bbQ}{\mathbb Q}
\newcommand{\bbR}{\mathbb R}
\newcommand{\bbS}{\mathbb S}
\newcommand{\bbT}{\mathbb T}
\newcommand{\bbU}{\mathbb U}
\newcommand{\bbV}{\mathbb V}
\newcommand{\bbW}{\mathbb W}
\newcommand{\bbX}{\mathbb X}
\newcommand{\bbY}{\mathbb Y}
\newcommand{\bbZ}{\mathbb Z}
\newcommand{\sA}{\mathscr A}
\newcommand{\sB}{\mathscr B}
\newcommand{\sC}{\mathscr C}
\newcommand{\sD}{\mathscr D}
\newcommand{\sE}{\mathscr E}
\newcommand{\sF}{\mathscr F}
\newcommand{\sG}{\mathscr G}
\newcommand{\sH}{\mathscr H}
\newcommand{\sI}{\mathscr I}
\newcommand{\sJ}{\mathscr J}
\newcommand{\sK}{\mathscr K}
\newcommand{\sL}{\mathscr L}
\newcommand{\sM}{\mathscr M}
\newcommand{\sN}{\mathscr N}
\newcommand{\sO}{\mathscr O}
\newcommand{\sP}{\mathscr P}
\newcommand{\sQ}{\mathscr Q}
\newcommand{\sR}{\mathscr R}
\newcommand{\sS}{\mathscr S}
\newcommand{\sT}{\mathscr T}
\newcommand{\sU}{\mathscr U}
\newcommand{\sV}{\mathscr V}
\newcommand{\sW}{\mathscr W}
\newcommand{\sX}{\mathscr X}
\newcommand{\sY}{\mathscr Y}
\newcommand{\sZ}{\mathscr Z}
\newcommand{\sfA}{\mathsf A}
\newcommand{\sfB}{\mathsf B}
\newcommand{\sfC}{\mathsf C}
\newcommand{\sfD}{\mathsf D}
\newcommand{\sfE}{\mathsf E}
\newcommand{\sfF}{\mathsf F}
\newcommand{\sfG}{\mathsf G}
\newcommand{\sfH}{\mathsf H}
\newcommand{\sfI}{\mathsf I}
\newcommand{\sfJ}{\mathsf J}
\newcommand{\sfK}{\mathsf K}
\newcommand{\sfL}{\mathsf L}
\newcommand{\sfM}{\mathsf M}
\newcommand{\sfN}{\mathsf N}
\newcommand{\sfO}{\mathsf O}
\newcommand{\sfP}{\mathsf P}
\newcommand{\sfQ}{\mathsf Q}
\newcommand{\sfR}{\mathsf R}
\newcommand{\sfS}{\mathsf S}
\newcommand{\sfT}{\mathsf T}
\newcommand{\sfU}{\mathsf U}
\newcommand{\sfV}{\mathsf V}
\newcommand{\sfW}{\mathsf W}
\newcommand{\sfX}{\mathsf X}
\newcommand{\sfY}{\mathsf Y}
\newcommand{\sfZ}{\mathsf Z}
\newcommand{\cA}{\mathcal A}
\newcommand{\cB}{\mathcal B}
\newcommand{\cC}{\mathcal C}
\newcommand{\cD}{\mathcal D}
\newcommand{\cE}{\mathcal E}
\newcommand{\cF}{\mathcal F}
\newcommand{\cG}{\mathcal G}
\newcommand{\cH}{\mathcal H}
\newcommand{\cI}{\mathcal I}
\newcommand{\cJ}{\mathcal J}
\newcommand{\cK}{\mathcal K}
\newcommand{\cL}{\mathcal L}
\newcommand{\cM}{\mathcal M}
\newcommand{\cN}{\mathcal N}
\newcommand{\cO}{\mathcal O}
\newcommand{\cP}{\mathcal P}
\newcommand{\cQ}{\mathcal Q}
\newcommand{\cR}{\mathcal R}
\newcommand{\cS}{\mathcal S}
\newcommand{\cT}{\mathcal T}
\newcommand{\cU}{\mathcal U}
\newcommand{\cV}{\mathcal V}
\newcommand{\cW}{\mathcal W}
\newcommand{\cX}{\mathcal X}
\newcommand{\cY}{\mathcal Y}
\newcommand{\cZ}{\mathcal Z}
\newcommand{\bfA}{\mathbf A}
\newcommand{\bfB}{\mathbf B}
\newcommand{\bfC}{\mathbf C}
\newcommand{\bfD}{\mathbf D}
\newcommand{\bfE}{\mathbf E}
\newcommand{\bfF}{\mathbf F}
\newcommand{\bfG}{\mathbf G}
\newcommand{\bfH}{\mathbf H}
\newcommand{\bfI}{\mathbf I}
\newcommand{\bfJ}{\mathbf J}
\newcommand{\bfK}{\mathbf K}
\newcommand{\bfL}{\mathbf L}
\newcommand{\bfM}{\mathbf M}
\newcommand{\bfN}{\mathbf N}
\newcommand{\bfO}{\mathbf O}
\newcommand{\bfP}{\mathbf P}
\newcommand{\bfQ}{\mathbf Q}
\newcommand{\bfR}{\mathbf R}
\newcommand{\bfS}{\mathbf S}
\newcommand{\bfT}{\mathbf T}
\newcommand{\bfU}{\mathbf U}
\newcommand{\bfV}{\mathbf V}
\newcommand{\bfW}{\mathbf W}
\newcommand{\bfX}{\mathbf X}
\newcommand{\bfY}{\mathbf Y}
\newcommand{\bfZ}{\mathbf Z}
\newcommand{\rmA}{\mathrm A}
\newcommand{\rmB}{\mathrm B}
\newcommand{\rmC}{\mathrm C}
\newcommand{\rmD}{\mathrm D}
\newcommand{\rmE}{\mathrm E}
\newcommand{\rmF}{\mathrm F}
\newcommand{\rmG}{\mathrm G}
\newcommand{\rmH}{\mathrm H}
\newcommand{\rmI}{\mathrm I}
\newcommand{\rmJ}{\mathrm J}
\newcommand{\rmK}{\mathrm K}
\newcommand{\rmL}{\mathrm L}
\newcommand{\rmM}{\mathrm M}
\newcommand{\rmN}{\mathrm N}
\newcommand{\rmO}{\mathrm O}
\newcommand{\rmP}{\mathrm P}
\newcommand{\rmQ}{\mathrm Q}
\newcommand{\rmR}{\mathrm R}
\newcommand{\rmS}{\mathrm S}
\newcommand{\rmT}{\mathrm T}
\newcommand{\rmU}{\mathrm U}
\newcommand{\rmV}{\mathrm V}
\newcommand{\rmW}{\mathrm W}
\newcommand{\rmX}{\mathrm X}
\newcommand{\rmY}{\mathrm Y}
\newcommand{\rmZ}{\mathrm Z}
\newcommand{\bb}{\mathbf{b}}
\newcommand{\bv}{\mathbf{v}}
\newcommand{\bw}{\mathbf{w}}
\newcommand{\bx}{\mathbf{x}}
\newcommand{\by}{\mathbf{y}}
\newcommand{\bz}{\mathbf{z}}
\newcommand{\paren}[1]{( #1 )}
\newcommand{\Paren}[1]{\left( #1 \right)}
\newcommand{\bigparen}[1]{\bigl( #1 \bigr)}
\newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)}
\newcommand{\biggparen}[1]{\biggl( #1 \biggr)}
\newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)}
\newcommand{\abs}[1]{\lvert #1 \rvert}
\newcommand{\Abs}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\card}[1]{\left| #1 \right|}
\newcommand{\Card}[1]{\left\lvert #1 \right\rvert}
\newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert}
\newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert}
\newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert}
\newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert}
\newcommand{\norm}[1]{\lVert #1 \rVert}
\newcommand{\Norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert}
\newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert}
\newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert}
\newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\Iprod}[1]{\left\langle #1 \right\rangle}
\newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle}
\newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle}
\newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle}
\newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle}
\newcommand{\set}[1]{\lbrace #1 \rbrace}
\newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace}
\newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace}
\newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace}
\newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace}
\newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace}
\newcommand{\bracket}[1]{\lbrack #1 \rbrack}
\newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack}
\newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack}
\newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack}
\newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack}
\newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack}
\newcommand{\ucorner}[1]{\ulcorner #1 \urcorner}
\newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner}
\newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner}
\newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner}
\newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner}
\newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner}
\newcommand{\ceil}[1]{\lceil #1 \rceil}
\newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil}
\newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil}
\newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil}
\newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil}
\newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil}
\newcommand{\floor}[1]{\lfloor #1 \rfloor}
\newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor}
\newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor}
\newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor}
\newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor}
\newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor}
\newcommand{\lcorner}[1]{\llcorner #1 \lrcorner}
\newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner}
\newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner}
\newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner}
\newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner}
\newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner}
\newcommand{\ket}[1]{| #1 \rangle}
\newcommand{\bra}[1]{\langle #1 |}
\newcommand{\braket}[2]{\langle #1 | #2 \rangle}
\newcommand{\ketbra}[1]{| #1 \rangle\langle #1 |}
\newcommand{\e}{\varepsilon}
\newcommand{\eps}{\varepsilon}
\newcommand{\from}{\colon}
\newcommand{\super}[2]{#1^{(#2)}}
\newcommand{\varsuper}[2]{#1^{\scriptscriptstyle (#2)}}
\newcommand{\tensor}{\otimes}
\newcommand{\eset}{\emptyset}
\newcommand{\sse}{\subseteq}
\newcommand{\sst}{\substack}
\newcommand{\ot}{\otimes}
\newcommand{\Esst}[1]{\bbE_{\substack{#1}}}
\newcommand{\vbig}{\vphantom{\bigoplus}}
\newcommand{\seteq}{\mathrel{\mathop:}=}
\newcommand{\defeq}{\stackrel{\mathrm{def}}=}
\newcommand{\Mid}{\mathrel{}\middle|\mathrel{}}
\newcommand{\Ind}{\mathbf 1}
\newcommand{\bits}{\{0,1\}}
\newcommand{\sbits}{\{\pm 1\}}
\newcommand{\R}{\mathbb R}
\newcommand{\Rnn}{\R_{\ge 0}}
\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\C}{\mathbb C}
\newcommand{\A}{\mathbb A}
\newcommand{\Real}{\mathbb R}
\newcommand{\mper}{\,.}
\newcommand{\mcom}{\,,}
\DeclareMathOperator{\Id}{Id}
\DeclareMathOperator{\cone}{cone}
\DeclareMathOperator{\vol}{vol}
\DeclareMathOperator{\val}{val}
\DeclareMathOperator{\opt}{opt}
\DeclareMathOperator{\Opt}{Opt}
\DeclareMathOperator{\Val}{Val}
\DeclareMathOperator{\LP}{LP}
\DeclareMathOperator{\SDP}{SDP}
\DeclareMathOperator{\Tr}{Tr}
\DeclareMathOperator{\Inf}{Inf}
\DeclareMathOperator{\size}{size}
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\min}{min}
\DeclareMathOperator{\max}{max}
\DeclareMathOperator{\argmax}{arg\,max}
\DeclareMathOperator{\argmin}{arg\,min}
\DeclareMathOperator{\qpoly}{qpoly}
\DeclareMathOperator{\qqpoly}{qqpoly}
\DeclareMathOperator{\conv}{conv}
\DeclareMathOperator{\Conv}{Conv}
\DeclareMathOperator{\supp}{supp}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\perm}{perm}
\DeclareMathOperator{\mspan}{span}
\DeclareMathOperator{\mrank}{rank}
\DeclareMathOperator{\E}{\mathbb E}
\DeclareMathOperator{\pE}{\tilde{\mathbb E}}
\DeclareMathOperator{\Pr}{\mathbb P}
\DeclareMathOperator{\Span}{Span}
\DeclareMathOperator{\Cone}{Cone}
\DeclareMathOperator{\junta}{junta}
\DeclareMathOperator{\NSS}{NSS}
\DeclareMathOperator{\SA}{SA}
\DeclareMathOperator{\SOS}{SOS}
\DeclareMathOperator{\Stab}{\mathbf Stab}
\DeclareMathOperator{\Det}{\textbf{Det}}
\DeclareMathOperator{\Perm}{\textbf{Perm}}
\DeclareMathOperator{\Sym}{\textbf{Sym}}
\DeclareMathOperator{\Pow}{\textbf{Pow}}
\DeclareMathOperator{\Gal}{\textbf{Gal}}
\DeclareMathOperator{\Aut}{\textbf{Aut}}
\newcommand{\iprod}[1]{\langle #1 \rangle}
\newcommand{\cE}{\mathcal{E}}
\newcommand{\E}{\mathbb{E}}
\newcommand{\pE}{\tilde{\mathbb{E}}}
\newcommand{\N}{\mathbb{N}}
\renewcommand{\P}{\mathcal{P}}
\notag
$
$
\newcommand{\sleq}{\ensuremath{\preceq}}
\newcommand{\sgeq}{\ensuremath{\succeq}}
\newcommand{\diag}{\ensuremath{\mathrm{diag}}}
\newcommand{\support}{\ensuremath{\mathrm{support}}}
\newcommand{\zo}{\ensuremath{\{0,1\}}}
\newcommand{\pmo}{\ensuremath{\{\pm 1\}}}
\newcommand{\uppersos}{\ensuremath{\overline{\mathrm{sos}}}}
\newcommand{\lambdamax}{\ensuremath{\lambda_{\mathrm{max}}}}
\newcommand{\rank}{\ensuremath{\mathrm{rank}}}
\newcommand{\Mslow}{\ensuremath{M_{\mathrm{slow}}}}
\newcommand{\Mfast}{\ensuremath{M_{\mathrm{fast}}}}
\newcommand{\Mdiag}{\ensuremath{M_{\mathrm{diag}}}}
\newcommand{\Mcross}{\ensuremath{M_{\mathrm{cross}}}}
\newcommand{\eqdef}{\ensuremath{ =^{def}}}
\newcommand{\threshold}{\ensuremath{\mathrm{threshold}}}
\newcommand{\vbls}{\ensuremath{\mathrm{vbls}}}
\newcommand{\cons}{\ensuremath{\mathrm{cons}}}
\newcommand{\edges}{\ensuremath{\mathrm{edges}}}
\newcommand{\cl}{\ensuremath{\mathrm{cl}}}
\newcommand{\xor}{\ensuremath{\oplus}}
\newcommand{\1}{\ensuremath{\mathrm{1}}}
\notag
$
$
\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}}
\newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}}
\newcommand{\nchoose}[1]{\ensuremath}
\newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}}
\notag
$
$
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}
\newcommand{\R} % real numbers
\newcommand{\N}} % natural numbers
\newcommand{\Z} % integers
\newcommand{\F} % a field
\newcommand{\Q} % the rationals
\newcommand{\C}{\mathbb{C}} % the complexes
\newcommand{\poly}}
\newcommand{\polylog}}
\newcommand{\loglog}}}
\newcommand{\zo}{\{0,1\}}
\newcommand{\suchthat}
\newcommand{\pr}[1]{\Pr\left[#1\right]}
\newcommand{\deffont}{\em}
\newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}
\newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation
\newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance
\newcommand{\xor}{\oplus}
\newcommand{\GF}{\mathrm{GF}}
\newcommand{\eps}{\varepsilon}
\notag
$
$
\newcommand{\class}[1]{\mathbf{#1}}
\newcommand{\coclass}[1]{\mathbf{co\mbox{-}#1}} % and their complements
\newcommand{\BPP}{\class{BPP}}
\newcommand{\NP}{\class{NP}}
\newcommand{\RP}{\class{RP}}
\newcommand{\coRP}{\coclass{RP}}
\newcommand{\ZPP}{\class{ZPP}}
\newcommand{\BQP}{\class{BQP}}
\newcommand{\FP}{\class{FP}}
\newcommand{\QP}{\class{QuasiP}}
\newcommand{\VF}{\class{VF}}
\newcommand{\VBP}{\class{VBP}}
\newcommand{\VP}{\class{VP}}
\newcommand{\VNP}{\class{VNP}}
\newcommand{\RNC}{\class{RNC}}
\newcommand{\RL}{\class{RL}}
\newcommand{\BPL}{\class{BPL}}
\newcommand{\coRL}{\coclass{RL}}
\newcommand{\IP}{\class{IP}}
\newcommand{\AM}{\class{AM}}
\newcommand{\MA}{\class{MA}}
\newcommand{\QMA}{\class{QMA}}
\newcommand{\SBP}{\class{SBP}}
\newcommand{\coAM}{\class{coAM}}
\newcommand{\coMA}{\class{coMA}}
\renewcommand{\P}{\class{P}}
\newcommand\prBPP{\class{prBPP}}
\newcommand\prRP{\class{prRP}}
\newcommand\prP{\class{prP}}
\newcommand{\Ppoly}{\class{P/poly}}
\newcommand{\NPpoly}{\class{NP/poly}}
\newcommand{\coNPpoly}{\class{coNP/poly}}
\newcommand{\DTIME}{\class{DTIME}}
\newcommand{\TIME}{\class{TIME}}
\newcommand{\SIZE}{\class{SIZE}}
\newcommand{\SPACE}{\class{SPACE}}
\newcommand{\ETIME}{\class{E}}
\newcommand{\BPTIME}{\class{BPTIME}}
\newcommand{\RPTIME}{\class{RPTIME}}
\newcommand{\ZPTIME}{\class{ZPTIME}}
\newcommand{\EXP}{\class{EXP}}
\newcommand{\ZPEXP}{\class{ZPEXP}}
\newcommand{\RPEXP}{\class{RPEXP}}
\newcommand{\BPEXP}{\class{BPEXP}}
\newcommand{\SUBEXP}{\class{SUBEXP}}
\newcommand{\NTIME}{\class{NTIME}}
\newcommand{\NL}{\class{NL}}
\renewcommand{\L}{\class{L}}
\newcommand{\NQP}{\class{NQP}}
\newcommand{\NEXP}{\class{NEXP}}
\newcommand{\coNEXP}{\coclass{NEXP}}
\newcommand{\NPSPACE}{\class{NPSPACE}}
\newcommand{\PSPACE}{\class{PSPACE}}
\newcommand{\NSPACE}{\class{NSPACE}}
\newcommand{\coNSPACE}{\coclass{NSPACE}}
\newcommand{\coL}{\coclass{L}}
\newcommand{\coP}{\coclass{P}}
\newcommand{\coNP}{\coclass{NP}}
\newcommand{\coNL}{\coclass{NL}}
\newcommand{\coNPSPACE}{\coclass{NPSPACE}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\LINSPACE}{\class{LINSPACE}}
\newcommand{\qP}{\class{\tilde{P}}}
\newcommand{\PH}{\class{PH}}
\newcommand{\EXPSPACE}{\class{EXPSPACE}}
\newcommand{\SigmaTIME}[1]{\class{\Sigma_{#1}TIME}}
\newcommand{\PiTIME}[1]{\class{\Pi_{#1}TIME}}
\newcommand{\SigmaP}[1]{\class{\Sigma_{#1}P}}
\newcommand{\PiP}[1]{\class{\Pi_{#1}P}}
\newcommand{\DeltaP}[1]{\class{\Delta_{#1}P}}
\newcommand{\ATIME}{\class{ATIME}}
\newcommand{\ASPACE}{\class{ASPACE}}
\newcommand{\AP}{\class{AP}}
\newcommand{\AL}{\class{AL}}
\newcommand{\APSPACE}{\class{APSPACE}}
\newcommand{\VNC}[1]{\class{VNC^{#1}}}
\newcommand{\NC}[1]{\class{NC^{#1}}}
\newcommand{\AC}[1]{\class{AC^{#1}}}
\newcommand{\ACC}[1]{\class{ACC^{#1}}}
\newcommand{\TC}[1]{\class{TC^{#1}}}
\newcommand{\ShP}{\class{\# P}}
\newcommand{\PaP}{\class{\oplus P}}
\newcommand{\PCP}{\class{PCP}}
\newcommand{\kMIP}[1]{\class{#1\mbox{-}MIP}}
\newcommand{\MIP}{\class{MIP}}
$
$
\newcommand{\textprob}[1]{\text{#1}}
\newcommand{\mathprob}[1]{\textbf{#1}}
\newcommand{\Satisfiability}{\textprob{Satisfiability}}
\newcommand{\SAT}{\textprob{SAT}}
\newcommand{\TSAT}{\textprob{3SAT}}
\newcommand{\USAT}{\textprob{USAT}}
\newcommand{\UNSAT}{\textprob{UNSAT}}
\newcommand{\QPSAT}{\textprob{QPSAT}}
\newcommand{\TQBF}{\textprob{TQBF}}
\newcommand{\LinProg}{\textprob{Linear Programming}}
\newcommand{\LP}{\mathprob{LP}}
\newcommand{\Factor}{\textprob{Factoring}}
\newcommand{\CircVal}{\textprob{Circuit Value}}
\newcommand{\CVAL}{\mathprob{CVAL}}
\newcommand{\CircSat}{\textprob{Circuit Satisfiability}}
\newcommand{\CSAT}{\textprob{CSAT}}
\newcommand{\CycleCovers}{\textprob{Cycle Covers}}
\newcommand{\MonCircVal}{\textprob{Monotone Circuit Value}}
\newcommand{\Reachability}{\textprob{Reachability}}
\newcommand{\Unreachability}{\textprob{Unreachability}}
\newcommand{\RCH}{\mathprob{RCH}}
\newcommand{\BddHalt}{\textprob{Bounded Halting}}
\newcommand{\BH}{\mathprob{BH}}
\newcommand{\DiscreteLog}{\textprob{Discrete Log}}
\newcommand{\REE}{\mathprob{REE}}
\newcommand{\QBF}{\mathprob{QBF}}
\newcommand{\MCSP}{\mathprob{MCSP}}
\newcommand{\GGEO}{\mathprob{GGEO}}
\newcommand{\CKTMIN}{\mathprob{CKT-MIN}}
\newcommand{\MINCKT}{\mathprob{MIN-CKT}}
\newcommand{\IdentityTest}{\textprob{Identity Testing}}
\newcommand{\Majority}{\textprob{Majority}}
\newcommand{\CountIndSets}{\textprob{\#Independent Sets}}
\newcommand{\Parity}{\textprob{Parity}}
\newcommand{\Clique}{\textprob{Clique}}
\newcommand{\CountCycles}{\textprob{#Cycles}}
\newcommand{\CountPerfMatchings}{\textprob{\#Perfect Matchings}}
\newcommand{\CountMatchings}{\textprob{\#Matchings}}
\newcommand{\CountMatch}{\mathprob{\#Matchings}}
\newcommand{\ECSAT}{\mathprob{E#SAT}}
\newcommand{\ShSAT}{\mathprob{#SAT}}
\newcommand{\ShTSAT}{\mathprob{#3SAT}}
\newcommand{\HamCycle}{\textprob{Hamiltonian Cycle}}
\newcommand{\Permanent}{\textprob{Permanent}}
\newcommand{\ModPermanent}{\textprob{Modular Permanent}}
\newcommand{\GraphNoniso}{\textprob{Graph Nonisomorphism}}
\newcommand{\GI}{\mathprob{GI}}
\newcommand{\GNI}{\mathprob{GNI}}
\newcommand{\GraphIso}{\textprob{Graph Isomorphism}}
\newcommand{\QuantBoolForm}{\textprob{Quantified Boolean
Formulae}}
\newcommand{\GenGeography}{\textprob{Generalized Geography}}
\newcommand{\MAXTSAT}{\mathprob{Max3SAT}}
\newcommand{\GapMaxTSAT}{\mathprob{GapMax3SAT}}
\newcommand{\ELIN}{\mathprob{E3LIN2}}
\newcommand{\CSP}{\mathprob{CSP}}
\newcommand{\Lin}{\mathprob{Lin}}
\newcommand{\ONE}{\mathbf{ONE}}
\newcommand{\ZERO}{\mathbf{ZERO}}
\newcommand{\yes}
\newcommand{\no}
$
A place to record my feeling, my thought, my exploration, and my growth. Since I intend to be casual here so I decided to use Mandarin for most of the posts. I'll translate some of the posts into English on request and put it
17 Sep 2022
實在不知道為什麼，連續兩年柴犬都剛好在夏秋交替之際生了場大病。雖然最終都發現是因為亂吃東西造成的，並沒有長期的隱憂，不過仍然帶來了許多心力的折騰，也讓這篇文章的撰寫推遲了一陣子。
隨著Ph.D.進入最後一年，身邊許多好友接連畢業，剛入學的大學生和博士一年級學生，更是稚嫩的讓人感嘆時間的飛逝。和這些小朋友聊著他們對研究生活的憧憬，似乎看見了當年的自己，雖然心中有說不完的經驗想要分享，最終卻笑著決定還是讓他們各自慢慢探索吧！這樣說起來好像有點理解為什麼每次當我問Boaz建議時，他總是很簡單的說跟隨自己的熱情就好。
這一年發生了什麼？
這一年美國總算基本上恢復了原本的生活，從課程轉回實體、各種設施的開放到更多和人們實際的交流，彷彿回到了剛來美國的時候，一切充滿了希望和幹勁。不過雖然大部分事情看起來都往好的方向走去，我卻開始對研究方向感到了十分困惑。
在接觸了越來越多不一樣的領域(特別是量子物理和腦神經科學)之後，讓我開始思考什麼樣的方法論是我想要追尋的。不可否認的，數學還是對我來說最舒服自在的語言，每次看到一個新的數學猜想或是理論都還是常常讓我興奮得睡不著覺。但同時我也越來越能適應物理的直覺，以及生物的複雜世界觀。然而身為一個學者，在學習之餘，還是需要有所謂的研究產出，那麼我希望在哪個領域做出貢獻？我是要繼續做數學證明、跑數值分析還是做實驗提假說？
在學年剛開始時，我很確定的是，我暫時不太想繼續在還有很多小問題可以做的streaming model上面花時間，但是我又不太想要直接用很理論CS的方式做一些量子和腦神經科學的問題。於是，我開始系統性的讀一些物理的教材，同時在原本就有的腦神經科學讀書會更系統性的學習不同的方向。既然都進入了學習的模式，甚至乾脆做了Science and Cooking的助教，然後修了一直很想學的音樂理論。這些不同的學習除了在知識層面之外，很意外的還讓我接觸到了不同領域”做理論”的方式。由於是理論CS背景的關係，理論對於我來說一直都是“數學理論”，好像沒有了嚴格的數學證明就不太能登大雅之堂。但無論是在讀物理教科書時發現裡面幾乎不會有完整的證明、在Science and Cooking中看到了許多應用物理推導公式的神秘方法、還有音樂理論中許多約定俗成的瑣碎規則等等。我才漸漸理解並且接受“理論”可以有的多重面貌。
整個秋季下來學習了滿滿的知識，也讓我決定該找個機會好好整理一下所學。於是利用學校的資源在寒假的時候弄了一個為期兩週的迷你課程，趁機把未來的方向理清楚一些。在準備課程以及講授的過程中，我也漸漸對於跨領域研究有了不一樣的理解(在下面的段落會再深入討論)，同時受到了Boaz不斷的提醒更是讓我意識到自己需要在許多的哲學性思考之餘，花更多的時間做實際的嘗試和工作(同樣的在下面的段落會再深入討論)。
到了春季學期，我更加深入的學習了量子計算和量子通訊，甚至還學了一些量子混沌及量子凝聚態。我突然意識到這些量子理論除了試圖解釋相對應的物理現象之外，更是提供了新的數學架構/語言能夠產生很多有趣的數學結構，這也是為什麼有些可以被應用在量子計算和量子機器學習上面。也許之後在其他的領域(例如腦神經科學)，這些數學工具能夠刻畫一些實際現象。如果這樣的理論被建構出來了，並不見得是說大腦裡真的用了什麼量子物理，而只是說剛好某些大腦中的運作可以被同樣的數學描述和理解。
暑假我很幸運的到了紐約的Flatiron Institute的Center of Computational Neuroscience跟SueYeon做暑期實習。雖然大家都開玩笑説我學到最多的是怎麼做咖啡拉花，不過認真講，這十個禮拜讓我更全面的接觸了理論和計算腦神經科學的各種面向。最大的影響應該是讓我意識到了即使是要做腦神經科學相關的研究，我可能還是需要把由上而下的抽象理論，跟與實驗接觸的問題區分乾淨，才能夠各自找到合適的解讀和應用。
在博士即將畢業前這一年，很感謝Boaz給了我這麼大的自由探索不同的領域和方法論，雖然因為把大部分的時間都花在學習和思考上所以沒有太多研究產出，但是感覺漸漸找到了有熱忱和適合自己的研究方向。而平時的胡思亂想，也讓我把一些做(跨領域)研究和學生的癥結處整理出了一套自己的觀點。在剩餘的篇幅中，就讓我來分享一下近來的體悟。
從跨領域(interdisciplinary)到多領域(multidisciplinary)
一直以來，即使是在理論CS之內，我都是研究涉略範圍相對比較廣的人，也因此很自然地走上了所謂“跨領域”的道路。在開始跟越來越多其他領域(主要是物理和腦神經科學)的學者合作之後，我漸漸意識到，跨領域雖然能將一個領域的工具或方法應用在另外一個領域，但是卻時常有個隱形的阻礙。要嘛是不同領域的人之間的溝通一直不在同樣的頻率上，不然就是做出來的結果四不像。這樣的情形在比較明確的工具轉移(例如機器學習用在分析數據等等)時比較不容易出現，然而在比較抽象或本質的理論跨領域交流時(例如計算複雜度理論和量子物理)卻屢見不鮮。
這種阻礙通常都是來自於跨領域的合作太過於直接，會有其中一方把自己的方法論和專業整套搬去另外一個領域，沒有足夠的修改與溝通來適應對方的歷史脈絡跟價值觀。正因如此，讓我突然意識到更深入的跨領域合作其實應該要把“跨”這個字拿掉。畢竟有了“跨”這個動作時，說明了不同領域之間有主次之分，但是在真正深入的交流時，應該是要互相汲取適合的想法，融會貫通。也許，我們應該像牛頓那個時代之前的科學家看齊，事先進入不同的領域，學習其根本的概念與價值觀，甚至各自有些基本的研究經驗之後，在試著做多領域(multidisciplinary)的研究。
一個需要特別釐清的點是，我的意思並不是說大家應該先進入對方的領域花個幾年學成之後，在開始進行合作。我想強調的點是，在某些和多個領域有關的研究問題上，如果合作的成員們還沒有成熟到可以自如地在各個領域之間轉換時，那可能還不如選定其中一個領域，然後好好的以那個領域的方法論做下去。這甚至也適用在同一個領域的不同子領域的交流中！說來慚愧，會有這樣的體悟也是因為我自己和幾個不同的合作者，時常在不同的方法論之間(例如量子計算優勢(quantum computational advantage)的理論和實務層面)來回擺盪，幾個月下來常常搞得什麼進展也沒有。
當然，如果能夠有可以順暢溝通的合作者，也許就不需要自己真的從頭學起另外一個領域。不過身為一個理論學者，為了自己思想的自由，我還是期許自己可以腳踏實地的真的把物理和生物的基礎和價值觀內化吸收。這幾年下來，雖然離理想的狀態還有些距離，但是已經可以開始感受到自己的視野越來越廣闊，想問題的角度也越來越多，非常期待之後在不同領域打滾幾年甚至是做了博後之後，能夠在多個領域之間來去自如的境界。
性格的重要性
一個人到底適合做什麼？從小到大總是會有些人說是依照興趣，另外會有些人說是靠天賦。的確天賦是進入某個領域行業的入門券，隨著不同職業門檻可能會有所不同。興趣則可以說是讓一個人能夠在一個方向一直做下去的驅動力。而最近我開始越來越注意到另外一項因子的重要性，那就是性格。
性格有非常多的層面，例如在著名的MBTI性格測試中定義了四個性格的軸向(能量來源、感知偏好、判斷偏好、認知態度)。同時性格相較於天賦來說，更容易受後天的環境和經歷影響，雖然可能到了成年之後會越來越定型。
為什麼我越來越覺得性格在職業適合度上扮演關鍵性的角色呢？這也得從自身的經驗說起。在我的求學階段初期，我夢想的職業是打棒球，而最後棄武從文，一直以來的說法都是因為運動天賦不足。上了高中之後，一直對物理和數學很感興趣，但因為當時缺乏對這兩個學科真實面貌的理解，最後大學選擇主修了CS。在大學四年中我大量接觸各式各樣的領域，在CS內從軟體工程到Bitcoin到理論CS，在主修外也學了很多數學和旁聽一堆不同科系的課，還曾經弄了個跨領域讀書會，一度有超過十個不同科系的成員。大學畢業後，為了能夠繼續在學校學習知識，選擇了讀了個理論CS的博士班。五年過去了，從前兩年在理論CS內做了好多不一樣的子方向，到現在開始廣泛接觸物理和腦神經科學。
這筆流水帳看下來，我發現了一個共同的規律，那就是我的性格無法讓我只專注在一件小方向/事情上面很久很久。又或是說，當我掌握一項能力到一定程度之後，我就會開始被其他新的事物強烈吸引，進而轉換方向開始學習新的東西。即使隨著年齡的增長，我漸漸在做事情的細心和耐心上面成長了不少，但是我依然很難抗拒學習新事物的誘惑。這樣的個性讓我很難在需要極度專一的領域上走下去，而我也總是不知不覺的被拉往相對需要多種能力的方向。
當然，性格不是只有一個面向，其他諸如好奇心、追根究底的精神、好勝心等等也都是帶著我一直走到現在不可或缺的角色。看看身邊的研究生同學和朋友，也許外人會覺得大家的共通點是所謂的“聰明”，但我反而覺得對熱愛事物的堅持才是這些博士生還有學術工作者的必要條件。
哲學思考與實際工作的平衡
年初有次在和Boaz聊天討論研究方向的時候，Boaz突然脫口而出，要我小心不要變得太像一個哲學家。我當時一直沒有很理解他的話，在我心中，一個好的科學家不是也應該需要花一定程度的時間做哲學思考，釐清楚自己工作的意義和貢獻是什麼嗎？
直到最近在翻Steven Weinberg寫的To Explain the World: The Discovery of Modern Science，才讓我重新思考了關於哲學和科學的差別。Weinberg從古希臘哲學家例如柏拉圖和亞里斯多德講起，提到在那個年代其實就已經有非常多關於對世界如何運作的“理論”，思想和學問的累積也是很有深度，那為什麼這些知識是被歸類為哲學？或是為什麼這些哲學無法帶給古希臘科學革命？我們又可以如何從他們身上學習到借鏡？
也許直接拿哲學和科學相比，實在會有太多的不同，不過我覺得真的要說的話，兩者之間有兩個根本的差異：首先是科學講求驗證，再來就是科學(在理想上)追求盡可能的客觀和共識。對於後者可能會牽扯一些不同科學哲學流派的不同解讀，所以在這邊我想要只討論第一點，驗證在科學中扮演的重要角色。
說到驗證，其實仍然避不開哲學的討論，尤其是像對於複雜系統或是高能物理等等，這些科學的子領域的確可能無法再看得見的未來有可能被嚴謹驗證。然而這邊我想強調的更是科學中一種“驗證的態度”。即使是研究複雜的腦神經科學，或是宇宙起源及大統一理論等等，即使大家都知道短期內不太可能有實驗能夠驗證檯面上的理論，但是多數主流的發展仍然會抱持著盡可能接近實驗的精神和態度。從學術界的兩大期刊，Nature和Science，基本上都要求要有實驗的潛規則中，就可以看出驗證在科學界中的核心角色。
而這種對驗證態度的要求，讓科學相較於哲學是非常的實務的，也就是大家會傾向於看到證據和實際的“工作結果”。這樣的工作結果可以是進行嚴謹的實驗，也可能是詳細的數學理論推導。縱使方法論因為研究的課題不同，會略有差距，但共通點就是強調“做”。譬如說前幾週和一個做量子重力理論的博士後聊天，他就跟我說，就算你有再多天馬行空的理論和想法，最終還是要回到計算來讓人信服。雖然這些數學理論還沒辦法在物理世界中被驗證，但是至少要能夠在數學世界中說服人！
回到Boaz給我的提醒，的確哲學思考固然可以提升思想的深度，但是也很容易落為眼高手低。人生有限，我選擇的又是一條科學/數學的道路，應該是要以工作和創造為主，天馬行空和自我批判為輔。就像許多人說的，最理想的學者狀態，也許就是個白天的科學家和晚上的哲學家吧！？
27 May 2022
趁著六月要去實習前的空擋，跑來參加了Simons Institute十週年研討會。研討會包含了二十個左右橫跨各種主題的演講，以及幾個討論理論CS未來發展的座談會。由於年底就要開始想想下一步要往哪裡去了，這個研討會可以說是一個讓我想清楚下個階段研究方向的的好機會。
首先不得不說這次Simons十週年研討會讓我對理論CS有了全新的認知，原本抱持著參加類似STOC/FOCS這種會議的心態，預期大部分的演講應該都是著重複雜數學技術。沒想到我完全跌破了眼鏡，整整三天下來(我第一次在一個會議中聽了所有的演講)，不光是主題的多樣性，連研究方式的豐富程度也讓我大開眼界。尤其是大部分的講者除了呈現了他們想要解決的研究問題和成果，更是在不自覺中展現了他們面對各自遇到的困難問題時，不同解決問題的方法論。在前往Berkeley的路上時，我還在想該如何問問大家對於數學證明之外的理論研究的方法論有沒有什麼看法，在聽了這些演講後，這個問題還沒被問出就被回答了。
而這幾年來我心中對理論CS發展方式的批判和質疑，也在會議劃下句點時跟著煙消雲散。我才終於發現到雖然會議中的主流文章越來越加複雜和脫離實際，但是還是有著一群領域內的大佬們試圖發展不同的方式，用理論的角度來試圖回答一些數學證明不太能觸及的問題。這邊我要澄清一下我還是非常喜歡數學證明，平常更是會不時學一些新的數學理論(像是上週末看了好多的代數拓墣)，不過同時我覺得數學證明不見得在所有跟計算相關的問題上都能夠得到令人滿意的解釋，甚至有時候過度追求完美的數學證明反而會失去了深刻的見解。
在聽了第二天下午的panel discussion以及和幾個前輩聊聊之後，更是讓我對於未來中長期的研究方向/方法論有了更成熟的圖像，感覺就像是重新地愛上了理論CS這個領域，對於未來充滿了興奮與期待。
對於「理論」的重新思考
語言真的是個很奇妙的東西，當年紀越來越大，很多詞彙的定義對我來說反而變得越來越模糊不清了。而「理論」大概就是一個很好的例子吧！(另一個讓我最近花很多時間思考的是「科學」)
年輕的時候，「理論」之於我來說就是抽象的邏輯推導建模，也就是設立基礎公設/公理/定義，然後從一系列的邏輯推演中得出理論理解。而理論CS的基礎教育也全部都是使用provable analysis，只有數學定理才能被稱之為理論。然而，這就是做理論唯一的方法嗎？或是讓我們退後一步，到底什麼是理論？理論的目的/意義/影響是什麼？理論可以有什麼樣的形式？
理論是什麼？
我很喜歡Wikipedia上對理論(Theory)的定義：
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking.
理論是關於一個現象的理性抽象思考，或是其產物。
但也許這個定義有點太哲學了，讓我們試著以它做為起點，來拼湊看看一些關於「理論」更具體的描述和性質。我認為，一個理論是個對於某些現象或是概念的知識體系。而這個體系中主要包含了(1)一套理論語言(2)知識形成和驗證的機制。
理論語言：說到一個理論使用的語言，可能馬上想到的就是相關學科的一些專有名詞。的確這是語言最基礎的一個層次，但理論語言通常可以提供遠遠高於定義層次的作用。
首先理論語言提供了一個思考事情的方式。例如達爾文的天擇論，提供了一套十分生動的語言，用擬人化(競爭/適者生存)的方式讓生物學家(甚至一般人)來思考和討論物種的演化。另外一個我很喜歡，但是可能比較需要一些數學經驗的人才能體會的例子是範疇論(category theory)。長話短說，範疇論提供了一套非常乾淨簡潔的語言，讓數學家可以用同樣的方式理解許多原本看似距離遙遠的數學概念。
更進一步，理論語言提供了一個領域規劃未來研究方向的基石。以電腦科學為例，計算複雜度理論(computational complexity)提供了複雜度類別(complexity classes)這套語言，讓人們可以非常具體的指出領域內重要的問題是什麼(e.g., P versus NP)。反觀一些還很缺乏理論語言的領域，諸如「什麼是intelligence?」等問題，會讓研究學者非常難以嘗試回答，因為甚至沒有什麼著力點。
而一旦理論語言被確立了之後，其實同時也為一個領域能夠回答的問題設了一個上限。就像哥德爾不完備定理(Gödel’s incompleteness theorems)告訴我們的，一個完善的邏輯系統總是有他無法解釋/證明的命題。即使是對非形式化的語言，我相信同樣的極限也是存在的，只是可能更難清晰的論證出到底那個極限在哪裡。
知識形成和驗證的機制：一個理論體系除了語言之外最重要的大概就是一套驗證知識的機制了吧！換句話說，就是該如何系統性且客觀理性地判斷什麼樣的論述可以被留存下來。
隨著所探討的學科和理論語言的不同，甚至和歷史發展或是學者的風格，每個領域的驗證機制或多或少都有些異同之處。而我認為大部分的驗證機制都可以被歸類為以下兩種類型的其中一種，或是在兩者中取了某種平衡：
形式方法(formal method)：
首先其實我原本想用的詞是「分析方法(analytical method)」，但是考量到一些領域對於分析方法有不一樣的詮釋，我決定用個比較不容易產生誤會的詞來解釋我想表達的概念。
對我來說，形式方法的論證機制的特徵是著重在根據一些共同認定或是假設(axioms/hypotheses)的基礎之下，使用數學證明和邏輯推演論證出更多的定理(theorems)，並且在眾多定理之下繼續往前推導出更多新的定理。而這些定理，以及人們對定理的詮釋，則構成了知識。在許多時候，推導定理的過程會產生一些意想不到的驚喜，而使得這些過程/數學證明往往也會成為知識的一部份。
數學毫無疑問地就是使用形式方法的最佳例子，而理論CS中大部分的子領域也都是使用這樣的方法論。在一些自然科學的理論分枝，像是一部份的理論物理或是理論生物研究，也會或多或少採用形式方法。
形式方法的優點在於，除了邏輯的嚴格性之外，它沒有太多其他的限制，因此有時候可以帶領人們思考地非常遙遠。很多的例子可以在理論物理中見到(e.g.,相對論、量子力學)，而在理論CS之中，許多有趣的概念也是受益於這樣自由的思考模式(zero-knowledge proof, probabilistic checkable proof)。不過這個優點的反面就是很容易受到完美邏輯論證的限制綁手綁腳，或是為了數學上的正確必須用非常冗長瑣碎的證明解釋一些其實很簡單的概念。
經驗方法(empirical method)：
絕大多數的科學學科(包括其比較理論的分枝)採用的都是經驗方法，也就是透過實驗觀察，或是數值模擬的方式來搜集事實(facts)及驗證假說。當然根據不同的學科和問題，會有不同的子機制(e.g.,不同的統計方法)來檢視什麼樣的觀察是合理的，在這邊我想強調的比較是經驗方法的最底層次是現實經驗，這也是為什麼我把數值方法歸類於此而非獨立成第三類驗證機制。
經驗方法與形式方法最大不同的地方就在於，它提供了事實(facts)，它告訴了我們且試圖解釋真實發生的實情。雖然經驗方法得出的一切觀察與理論都還是參雜了一些人為的推論的解讀，但是本質上它是服膺於實際發生現象。也因此，經驗方法的底線是(在論證”合理”之下)符合和解釋現實。
So what?
寫了這麼多看起來像是廢話的東西，我們終於可以來討論我對「理論」重新思考的重點了。由於我其實也還在塑建自己想法的過程中，所以以下我將會用提出問題的方式來呈現我的思考，希望可以激發讀者做一些深入的思考，也期待這些問題可以漸漸地找到一些有意思的回答。
現有理論方法論的邊界？私認為現有的理論方法論走到了兩個轉捩點。其一是形式方法進入到了近乎巴洛克風格的階段，越來越複雜且和現實脫離。其二是機器學習/深度學習帶來經驗方法的革命，各種人類無法理解但是實際上有效的方法(e.g., Alphafold)大量湧現。前者警示了我們傳統完美數學邏輯論證的方式似乎進入了緩慢成長且窄門化的境界，後者則是挑戰了現有理論方法能夠處理的邊界。我們是否真的能依賴一直以來的方法論們來處理這些舊時代遺留的重要問題和新時代產生的新問題？我們是否需要新的理論架構？
如何構造不同層次的理論語言？對於上述的問題，我個人認為的突破口是建立一系列服務不同層次理解的理論語言。現有的理論語言大多要麼是純粹數學邏輯化的，要麼是描述性(descriptive)的，鮮少能有介於之間且能夠順暢翻譯的語言。一個好的例子可能又是達爾文的天擇論，這個理論架構中不但有一套比較方便溝通類比的直覺性語言(e.g., 適者生存)，同時有比較機械化的中層語言(e.g., 適應性地貌(fitness landscape))，還有底層的數學語言(e.g., 演化動力學(evolutionary dynamics)){:target=”_blank”})。對於那些卡在底層數學證明的問題，我們是否能夠往上一層建立個不完美但堪用的理論語言？
有什麼混用形式方法與經驗方法或是其他的方法論？物理學可以說是最成功將純粹抽象數學推導和實驗觀察結合的學科，其他的領域是否能夠也有這樣混合並用的方法論？其實每個領域或多或少都有不同程度的混用這兩種截然不同的方法論，只不過子領域之間的隔閡造成不良的溝通。而根本的原因可能還是目的與審美的不同，導致形式方法與經驗方法漸行漸遠。也許要形成新的方法論沒有想像中那麼的難，真正的挑戰反而是在於如何接壤過去舊有的學派，展開心胸接納不同的方法。
22 Jan 2022
(See here for an English version)
這一個月來幾乎八成的時間都是在準備這個為期兩週的mini-course，未料在最後幾天，一個小插曲讓我重新認真思考了一下科普的本質倒底為何？我們真的需要科普嗎？科普會不會反而讓科學的進展開倒車？
先讓我們試圖釐清科普的定義吧！仔細想想的話，科普可是有非常多不同的形式和層級呢！
新聞媒體：“達爾文進化論被推翻了！”，這大概是一般人生活中最常接觸到的科普吧？各種新聞媒體到網路影片工作者，每天都有無數的人試著把最前沿的科學研究用淺顯易懂的方式傳達給大眾。當然這種形式的科普品質十分參差不齊，在市場競爭的叢林中，有些人靠聳動標題維生，有些人則是堅持專業獲得死忠粉絲。
科普書籍：如果更有一些時間和心力，一般人接下來會接觸到的大概就是科普書籍了。同樣的，書店中科學區的書架上，琳琅滿目，各種名人以及得獎科學家的加持，範圍更是從物理、化學、數學到生物、心理學等等。跟新聞媒體最大不同的地方是，科普書籍通常具有較完整的系統，有些甚至一出手就是四、五本一套。然而畢竟不是教科書，面向的是普羅大眾，科普書籍通常還是使用非常淺顯的敘述，不會假設太多的教育背景，很多時候甚至會省略掉一些有點重要的概念。
線上課程：有時候還真的挺羨慕現在的小朋友，在網路上很輕易的就可以免費看各種大學教授開設的線上課程。儘管許多時候這些線上課程被簡化了許多，但是透過作業以及網路論壇互動，甚至是簡單的實驗，是可以獲得科普書籍無法做到的學習效果。
大學通識課程：這也許是科普中最高的層次了吧？在大學通識課程中，教授們不但有整個學期的時間，同時學生們受過基本教育的訓練，即使可能來自稍微不同的背景，但是相對於一般民眾，可以假設這些大學生具有流暢的邏輯思辨和溝通能力。例如我在上學期助教了一門「Science and Cooking」的通識課(這門課同時也有線上版本，但是簡化了非常多)，老師們在短短三個月中，讓來自不同學院的學生們淺嚐了諸如elastic modulus、diffusion equation等等在(初階的)專業課程中才會學到的基本概念。
至於我的mini-course在哪個層級呢？我自認為大概是介於線上課程和大學通識課程之間，因為課程內容在廣度的要求之下相對犧牲了深度，但是同時我也期許自己能夠盡可能的放入很多精髓讓學生在未來可以繼續探索。而下一步我也打算著手寫一本相關的科普書籍，希望用不同的形式呈現我對這些跨領域知識的理解和看法。
科普的目的是什麼？
我想每個人可能都對科普的目的有略微不同的看法，有些人覺得是為了讓艱澀的科學知識更容易讓大眾接觸，有些人覺得這是個很好增加知名度的方式，有些人可能是很享受教學和寫作的過程。
不過以我的例子來講，其實說來慚愧有點自私，最初的原因主要有兩個：首先是這樣可以讓我身邊的家人和朋友更知道我在做什麼，像是我在大學畢業前寫了一本「探索計算的極限」，講解了基本的計算理論概念，最後分送給朋友和家人。雖然最後我爸媽好像還是沒有看完，不過至少例如我的設計師好友小羊，在完全沒有相關背景的情況下，花了半年的時間讀完後，現在大約知道二進位制和圖靈機是什麼了！第二個原因則是透過科普的寫作，其實對我自己來說是一個沉澱和昇華的過程。在之中我會不斷地挑戰自己最底層的理解，接著試圖猜測潛在讀者可能會困惑的地方，在一來一回中琢磨出連我一開始可能都意想不到的敘事和理解方式。
但是這樣的動機的確可能還是稍嫌薄弱，看看我在這個mini-course所花費的心力，似乎不成比例。的確，另外一個科普(還有教育in general)帶來很大的附帶品就是和聽眾/讀者/學生的互動。這種互動和前述有些人追求的知名度是不一樣的，更像是一種找到知音的快樂。話說回來，終究還是自私的讓自己開心。
難道對我來說科普的目的就只有這樣嗎？如果站在客觀一點的角度來看，我是有些話想說。
首先我認為在現在的教育體制下，知識還是非常分配不均的。我一直到進了台大之後，才發現高中以前我竟然錯過了這麼多，如果當你連碰到好的書和教材的機會都沒有，那麼再怎麼聰明的人也是無法從無到有變出人類累積千百年的智慧。而到了Harvard之後，我更驚覺big picture的重要。當先建立了好的基礎觀念以及了解一個領域的大方向結構和價值觀，學東西的效率完全是提升好幾個層級。然而無論是好的教材或是big picture，即使在現在網路發達的世代，仍然還是沒有那麼容易讓一般人接觸到。
Everything should be made as simple as possible, but not simpler.
所有事物都應該被盡可能的簡化，但是不能簡化過頭。
- Albert Einstein.
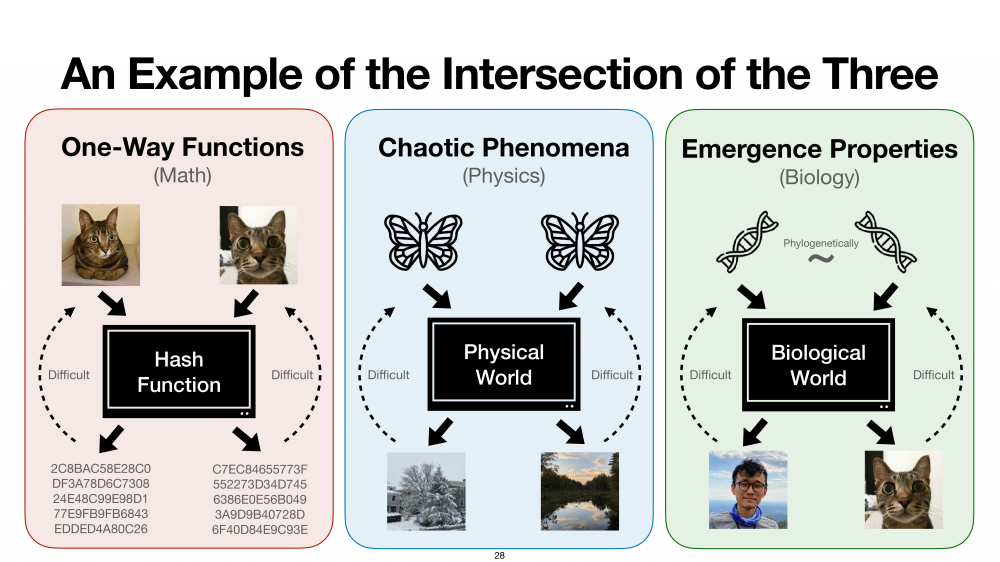
此外，我覺得科普在現代社會還有另一個特殊的角色，那就是增進領域之間的交流和學習，這也是我這門mini-course的核心價值。在當今各個領域都蓬勃發展，且變得越來越複雜艱澀之後，跨領域學習面對的牆變得越來越高越來越厚。同時跨領域互動的目的也和本科學習的目的有些不同，更多的是在交流彼此的核心概念，藉此激發出在各自領域的新想法。
科普的危險
接下來讓我們進入本文的核心討論：科普是不是危險的？
以我的觀察來看，認為科普產生弊大於利的論證，主要著重在於(1)科普會讓一般人有種覺得懂了很多的錯覺(2)科普讓人變得懶惰而不扎實的學習(3)科普過度簡化甚至可能造成科學進展的倒退。
首先我非常認同前兩點，一些“不好”的科普的確很容易衍生這樣的社會問題。但是我也想指出這種論證的一個盲點：會因為讀了科普而產生懂很多的錯覺或是對學習懶惰的人，他們並不會因為沒有了科普就變成一個上進的人！相反的是，如果有個好的科普，能夠讓人在學習的過程中反而更發現自己的無知，這樣反而達到正面效果，人們會因此更知道自己缺乏什麼而繼續學習。而這也完全是我在我的mini-course想要跟學生們傳達的！在這邊也跟大家分享一個我不斷跟學生強調的一個quote：
Our knowledge can only be finite, while our ignorance must necessarily be infinite.
我們的知識只能是有限，同時我們的無知必定是無限。
- Karl Popper.
所以對我來說，(1)和(2)更像是對科普推廣者的提醒，而非真正的危險。
至於(3)，這個就非常的subtle了，身為非常資淺的學術工作者，我在這邊只敢提供一些小小的評論，同時希望可以激起更多對於類似議題的討論！
首先，科學是不斷地進步的嗎！？沒辦法讓科學”進步”的就不配被稱為好的知識或研究嗎？如果是一直身在學院的象牙塔中，一路吸收所謂“正確”的科學知識，那麼的確看似只要跟最後留下來的理論不相符的都可以被稱為沒用。然而這絕對不是科學發展真實的面貌，綜觀科學史，現在最終留下的理論，很多是奠基在如今被視為不那麼正確，或甚至在當初有些誤導人的理論。而在科學發展的前沿，我們也知道許多如今被視為傑出的理論，在一開始通常也都是在許多略有錯誤的理解和猜想中，慢慢修正孕育出來的。
最後，我個人認為，把科學的論述單一化是非常危險的，這樣反而更容易阻礙科學的進展！讓我們從演化的角度來看看，如果沒有什麼變異，那麼雖然現在這個理論把世界解釋的很好，但同時也意味著改變或”往前”的動力是比較小的。反觀在變異大的情況下，縱使會先產生許多被淘汰掉的變種，甚至走倒車，但是需要透過這些變異，才可能讓我們更有機會產生下一個“典範轉移”！
自我省思與期許
寫到這邊，我希望我至少能夠暫時說服讀者如果有“好的科普”，那麼對於社會、科學發展、跨領域交流，都是利大於弊的。不過最終就必須正視我所謂“好的科普”是什麼？會不會這樣的理想在現實中是不可行的？該如何分辨科普的優劣？
我覺得，一個“好科普”的必要條件，是清楚地讓讀者或學生知道有什麼東西是被省略的、有什麼東西是我們還不知道的。畢竟知識本身最終還是由接受的一方詮釋，再好的老師或是再好的書，都無法控制別人如何解讀(同時這也是科學非常“社會化”的一面)。於是在知識本身的呈現之外，適時的提醒便顯得非常重要。其實話說到底，即使離開科普的討論，在科學的學習和研究中，抱持謙卑和清楚地知道自己不懂什麼，也是不可或缺的。下圖是個我的mini-course中最後一堂課中的投影片，在這邊作為一個警惕與期許。
至於理想中的好科普是否在現實中可行？我覺得這個問題就像是在問科學家是否可以找到理想中的完美理論一樣，到頭來可能更接近於個人信仰了。至少我個人是保持樂觀，在市面上的確也看到一些對我來說還不錯的書或是課程。但至於該如何辨別科普的優劣，這個可能真的就只能靠個人修煉了。任何的書或是課程，都是會有正面和負面的聲音同時出現，有時候正面音量大也不見得代表就是好的，反之負面音量大也不代表一無可取。最終雪亮的眼睛以及批判的閱讀，才是能夠帶領一個人在知識之路顛簸向前的路燈。
最後，也想留幾句話給未來的自己作為一個警惕。在受到刺激的時候，別急著反駁，甚至不小心忘記了檢視自己的問題。人都會犯錯，最重要的是坦然面對自己的錯誤，並且在之中成長。期許自己，be confident but also be humble, be curious but also be rigorous。
20 Dec 2021
In the following January, Harvard GSAS kindly supports me to offer a mini-course on “What is Computation? From Turing Machines to Blackholes and Neurons”. In this blog post, I’m going to share the motivation for teaching this mini-course and give an overview on what you will learn if you are interested in participating!
Computation is not an exotic word for people living in the 21st century. In high school, kids have to learn and do all sorts of computations in arithmetics (and some even start to write computer programs!). For scientists, computational methods become more and more common and sometimes even completely change the paradigm of a field. There are computers of different forms hiding in our daily life ranging from your smartphones to the toy of your pets. Also, from time to time we see excitement on the news about the development of quantum computing and artificial intelligence. Computation has become central in human civilization, however, do we really understand what computation is?
Let me first convince you why asking and attempting to answer this question is important.
Traditionally, at least on Wikipedia, computation is defined as “any type of calculation that includes both arithmetical and non-arithmetical steps and which follows a well-defined model (e.g. an algorithm)”. Indeed, for computer scientists and mathematicians, computation is about solving computational problems via an abstract mathematical model known as Turing machine. In particular, the Church-Turing Thesis, which can be viewed as Newton’s laws in computer science, asserts that all effective computational methods in the world can be captured by Turing machines. That is to say, in the mathematical world, computation is something axiomatized and can be studied and understood parallel to the empirical world.
On the other hand, for the majority of people, computation is something more concrete and has a physical realization such as a digital computer. The rise of computer science in the past few decades is certainly owing to the great technological success of building up modern computers. The fascinating advances of technology seem to close the gap between theory and reality (similar to Newton’s laws!). Nevertheless, in the frontier of scientific research, the recent surging developments of quantum computing and artificial neural networks started to challenge our understanding in computation - the ways they compute are so different from the traditional Turing machines and we don’t really know why and how they work so well!
In my opinion, we need to revisit the notion of computation in order to attack these mysteries. Specifically, the approach should be interdisciplinary.
As computer scientists are used to think of computations as composing different resources and subroutines, the computations in physics and biology tend to be rather holistic and open-ended. When talking about computations, people from different fields often think a bit differently. Such distinctions across fields should not be barriers or problems, instead, it could potentially serve as seeds to enrich our understanding in the essence of computation.
This mini-course is an invitation to rethink about what computation is through different angles. We will focus on but not limit to three perspectives including mathematics, physics, and biology. Through theories, examples, and experiments, we are going to see the similarities and differences between these disciplines. Six guest speakers coming from a diverse background (from computer science and physics to neuroscience and modern art) will join us and provide lots of examples and stories from their home field. The aim of this mini-course is to remind people of the diverse nature of computation and envision the possibilities of future interdisciplinary research.
There will be three modules and each contains three 50-minute interactive lectures and 1-3 guest talk(s). The first module focuses on the mathematical foundation of computations in which the students will learn the concept of Turing machines, computability, reductions, and most importantly, the underlying philosophy. The second module is about the computations in the physical world where we will launch from classical mechanics, to statistical mechanics, quantum mechanics, and gravity. The third module looks into the computations in biology, ranging from genomes, evolution, to neuroscience. The mini-course will end with a panel discussion with all the guest speakers and students.
Please visit the course website for more information and hope to see you in January!
28 Nov 2021
(See here for an English version)
今年波士頓的九月(注：這篇文章起筆於十月初…)，沒有延續暑假的熾熱，反倒充滿了秋意。每當傍晚騎車越過查爾斯河的小橋時，迎面而來的冷風，讓人彷彿置身在冰水中游泳般，十分暢快。原本預期楓葉會因此提早來訪，然而十月第一個週末的理論組賞楓健行，意外的沒有被想像中繽紛的色彩包圍，果真理論和現實還是有差距呀！
才剛踏上Mt. Monadnock的白點步道，就和一個新來的博士後熱絡的聊起了CS和Neuroscience的跨領域研究。先是互相約略分享了一下各自正在探索的問題，接著談起生物研究和CS以及物理研究的不同。什麼樣子的生物研究是“接近現實的”？如何評判一個數學理論模型是“合乎生物性(biologically plausible)”的？在我們倆口沫橫飛的激辯過程中，一瞬間，我突然從他的眼中看到了一個是如此明顯，但是我至今才終於意識到一個生物學家和電腦科學家(以及數學家和物理學家)之間的鴻溝：原來雙方在談論biological plausibility時，心中想的是完全不一樣的東西！
身為受到CS訓練出生的一份子，當我們提到biological plausibility時，心中基本上想的不乏是列下好多個“限制條件”，例如神經元之間的連結通常很局部、神經元的活動通常很稀疏等等。接者再用數學語言刻畫這些限制條件，並且開始一連串的抽象理論推導或電腦模擬分析。然而對生物學家來說，biological plausibility其實並不見得是這麼具體的條列檢查項目，而比較像是通過大量的閱讀和討論後，建構出一個自己以及領域內的世界觀。生物實驗實在充滿太多雜訊以及特例，基本上不可能列出嚴謹的數學條件逐一客觀的檢查，也因此會產生一些很有趣的現象：生物學家有時候反而會沒有電腦科學家想像的如此biologically plausible！
跨領域的研究充滿了挑戰，除了要學習大量其他領域的知識，我覺得最困難的是如何理解和欣賞其他領域的美。在今年暑假前偶然在Facebook上看到朋友推薦了演化生物學大佬Ernst Mayr在二十多年前寫的This is Biology，讓我終於有機會系統性地一窺生物學家心中的生物學到底是什麼樣貌。
一趟建構生物哲學的雲霄飛車之旅
原本只是打算拉著做演化生物學研究的室友一起讀This is Biology，想和他討論以及聽聽他專業的見解，結果他很熱心的組織了一個讀書會，邀請了幾個來自不同領域的朋友，開始了這段建構我的生物哲學的雲霄飛車之旅。
之所以稱之為雲霄飛車，是因為我的心境變化在這三個月中不斷受到挑戰與改變，如今列車緩緩進站，帶著重新建構的價值與信念，下了車準備展開下一段旅程。未來在跨領域研究的路上，一定還會在受到許多刺激和成長，趁現在記憶猶新之際，讓我簡單記錄一下This is Biology帶給我的啟蒙與轉變。
生物學中的美與挑戰
之前和一個做物理的朋友聊天時，常聽他開玩笑說生物學就像是集郵一樣，它的美是在大自然中的多樣性及複雜，而生物學家的工作就是搜集紀錄各種新的發現。相比之下，物理和數學似乎更加“深入”地探索了自然及抽象世界中隱藏的對稱與結構之美。言下之意，往往就會有種優劣之分的階級感浮現。確實物理學家中普遍有種自信，認為自己對於世界有更深刻的理解，而生物學相對起來年輕許多，在許多子領域中還留在做實驗搜集資料的階段。但這樣的現況並不代表哪一門學科比較難或是比較簡單，當走到一個領域的前端時，只要保有著對於對知識的好奇、對學問的嚴謹、對品質的堅持，每往前一步都有其無法比較和取代的意義。
從小我在一個很少接觸大自然的環境中長大，在城市的車水馬龍和數理抽象世界的烏托邦之間，我一直以來無法理解和欣賞生物學的美。還記得剛認識室友的時候，一聽到他要花一兩年的時間幫蝴蝶標本拍照，寫程式分析翅膀的顏色和形狀，我實在很難接受這樣也算是“做研究”。為什麼要花這麼多時間在千萬種生物的其中一種上？為什麼每個種類的蝴蝶搜集六隻標本就足夠做統計分析？為什麼可以在如此不明顯的關聯性分析得出任何推論？
的確，如果從物理和數學本位的角度來檢視，生物研究可能登不上“大雅之堂”。但是為何生物學需要跟物理和數學相提並論呢？將這幾門不同的學科直接比較就像是把音樂和繪畫做比較一樣，個人的主觀喜好會影響理性客觀的思辨。追根究底，由於“審美觀”的不同，造成了不同學科之間的誤解甚至歧視。所以就讓我先從我對生物之美的重新認識作為一個開端，放下成見，試著描繪生物世界的審美觀究竟為何。
從集郵到拼圖：多樣性之美、個體之美、實驗之美
生物學之所以被開玩笑地貼上集郵的標籤，不外乎就是因為生物多樣性。世界上已知的次原子粒子有幾百種，而地球上光是蝴蝶就有將近兩萬種。如果更仔細去想何謂不同的生物種類，就會發現連光是如何好好的定義“物種”都已經是一個非常不簡單的工作了。既然生物多樣性是如此的瑣碎繁雜，那麼它到底美在什麼地方呢？從表面上看起來，的確就像是集郵一樣辨別和搜集不同的物種，這就是多樣性之美嗎？對我來說，這種”集郵之美“只是生物多樣性中的第一步而已，而生物學家在做的則是要在千千萬萬的物種之間，規約找出背後的規律及異同。
因此我覺得生物的美更多是在於集郵之後的”拼圖“階段。如何在雜亂的實驗數據(i.e., 拼圖碎片)中把有關聯的聚集在一起、如何不受到表面相似性的影響(e.g., 下圖中的貓咪拼圖，同樣是橘色的圖塊，可能是來自於不同的貓咪！)、甚至是如何在缺乏整體圖像(e.g., 想像玩拼圖的時候不讓你看到最後的圖像是什麼)的情況之下，試圖拼湊出些什麼有意義的結果。
至於物理和數學，則比較像是棋盤遊戲和策略遊戲，在少數的規則和龐大的可能性中，堆疊開闢出一條蹊徑。
於是，要建立對生物學的審美觀，需要先暫時放下對從邏輯底層往上前進的堅持，著眼在如何由上而下的把龐大雜亂的資訊梳理乾淨(當然在數理學科也有許多由上而下的美與挑戰，這邊我只是用一個最宏觀的角度來區分生物研究和其不同之處)，如果無法欣賞這部分的有趣和美感，那麼可能將會有點困難去進一步體會近代生物研究發展的美。同時在這邊我也想強調，這篇文章的目的不是要說服所有讀者都要能夠欣賞生物之美，而是著重於剖析生物和物理(及數學)本質的差別，然後提出我觀察到不同領域誤解和歧視的癥結點。
當開始可以欣賞生物學中由上而下的“拼圖之美”之後，接下來就會有更多可愛之處可以探索，在這裡我要跟大家分享三個我近期的體悟與感動，分別是多樣性之美、個體之美、實驗之美。
多樣性之美：以前我一直不太能理解每次我室友看到沒見過的螞蟻品種時，為什麼會那麼的興奮(其實現在我也沒有全然理解…)。現在回想起來，最主要是因為過去的我對於美感的追求是更為抽象、型式與對稱，而生物多樣性之美則幾乎是硬幣的另一個反面，欣賞的是具體、實作與特例。兩種美感雖然很不一樣，但是並不互相衝突。因為成長以及學習環境的不同，每個人的確也會對於這兩種美有不同的傾向。當然，一個人不需要強迫自己去欣賞另外一種美，不過當審美的視野被打開了，除了生活增添更多色彩之外，多樣性之美更是時常帶來許多的靈感。
個體之美：每個人在這個世界上都是一個獨一無二的存在，不像是宇宙中的每個氫原子基本上看起來和觀測起來都是一樣的。雖然在前幾段我才說生物學家的工作就是在多樣性中尋找出規律，但也正因為生物世界中的個體總是存在著差異，在發現規律的同時，更是讓我們能夠從個體和規律的偏差之間重新給予其新的理解與認識。生物學中理論的建構，在追尋背後支配現實的規則之餘，可以說是給我們一個新的觀點和角度去理解個體之美。
實驗之美：當物理是要透過精準的實驗驗證理論模型時，我會覺得生物實驗更像是從稀少的資源中試圖以管窺豹。當前面說到我室友的蝴蝶研究中每個物種只用了六隻個體，這並不是說他們不想要用一百隻，而是現實上不允許他們這樣做。於是實驗上的限制(e.g., 蝴蝶的個數、數據中的雜訊)就好比是數學推理中的邏輯規則，生物學家如何在各種限制中設計出有意思的實驗方法，不亞於數學家在邏輯公設中殺出一條血路。差別主要在於這些限制的數量和具體程度，以及邏輯推演的長短。
這邊提供neuroscience中兩個關於decision making的經典實驗，讓讀者體會實驗設計背後的巧思與美感。
首先提供一些背景資訊，在decision making相關的研究中，neuroscientists的(短期)目標是要找到具體的神經網路配置，清楚地對應到一個決策機制。因此最大的挑戰就是該如何盡可能地排除其他可能性，讓實驗結果(只)能被他們提出的理論解釋。於是在一個實驗中，除了各種錄製神經訊號的儀器之外，還需要設計動物行為以及解讀不同的行為結果。
第一個實驗是關於觸覺的decision making。一隻猴子的手指會先被一個20赫茲的震動刺激了500毫秒，再過了一陣了之後，會被另外一個頻率的震動刺激500毫秒。接著猴子必須按鈕決定第二次震動的頻率是比前一次高還是低。
第二個實驗是關於視覺的decision making。一隻猴子首先要盯著一個屏幕上十字，同時看到旁邊有一些小點點全部往左或全部往右移動。最後當十字和小點點同時消失時，猴子必須向右或向左看來表示他覺得小點點大部分是往右還是往左。在比較困難一點的版本，有一部份的小點點會隨機往任何方向移動。
上述這兩個都是非常經典的decision making實驗，但是有沒有其中一個設計得比另一個更為巧妙呢？如果仔細想想的話，就會發現第一個實驗有個很大的問題：兩個震動刺激之間隔了一些時間，因此猴子的大腦需要先“記住”第一個震動，接著再和第二個震動做比較。如此一來增加了可能性的複雜度，而實際上當年的實驗結果也的確無法很好的解釋猴子是如何做決定的。至於第二個實驗，首先透過同時呈現所有資訊來避開了記憶的問題。此外，用不同比例的隨機小點點可以更量化的理解神經網路的機制。先用十字來提醒猴子實驗要開始了更是一個”重新開機“的手法，確保每一次實驗的開端都是差不多的。
不同的挑戰：對稱性的缺乏、湧現性質、客觀意義
如果要再更進一步的建立對生物學的審美觀，就必須正視和理解其面對的挑戰。在這邊我想要著重在三個我個人覺得生物學面臨地最大挑戰：對稱性的缺乏、湧現性質、客觀意義的存在與否。
對稱性的缺乏：近代物理的偉大成就，可以說是建立在對於物理世界中的對稱與不對稱的精闢觀察。對稱性引領出了豐富的數學，使得純粹抽象的分析有了可能(推薦閱讀：The Unreasonable Effectiveness of Mathematics in Physics)。然而在生物的叢林中，極度缺乏豐富多樣的對稱性，這也是我認為建立好的生物理論最困難的根源。於是雖然看似生物領域中有非常多的數學或計算模型，這些模型更像是一種“描述”而不是像基礎物理模型“刻畫”了真實(不過以我對數學模型是“描述”還是“刻畫”的定義，應用物理許多的研究也是屬於前者)。
湧現性質：生物中所謂的湧現性質(emergence property)其實跟物理中的 混沌現象(chaotic phenomenon)基本上是同一個概念：簡單的規則在大量的使用後產生複雜的結果。我個人更喜歡用理論CS的一個概念來思考湧現性質：單一方向性(one-wayness)，也就是說正向運算很容易，但是想要逆推回起點是困難的。一個胚胎如何發展成成熟的個體？基因是如何對應到表型(phenotype)？神經元的活動是怎麼形成計算、智能、意識？我認為湧現性質使得機械性的模型與理解變得極為困難，要嘛我們只能得到很粗淺的宏觀統計，要嘛就是模型本身變得極為複雜無法被理解(e.g., 用深度機器學習去建立模型)。同時，物理時常用到的簡約(reduction)方法也因為湧現性質而變得不太可行。我們也許需要一套有別於現有物理與數學的方式來理解湧現性質？
客觀意義：人類總是傾向賦予事物一些意義。還記得上次去羚羊谷(Antelope Canyon))旅行時，除了被大自然的鬼斧神工震撼之外，更是見識了當地導遊的創意。在短短一英哩的路程中，每走幾步導遊就會突然指著岩壁喊著：「看，這是海底總動員裡面的那隻鯊魚！」(如下圖)之類的話。我相信沒有人會覺得大自然是故意侵蝕出一隻鯊魚在羚羊谷裡面，同時這也警惕著我們在面對自然的時候更應該注意放下過多的人為解釋。這不禁讓我想到書裡討論到在過去和近代對於近因與遠因(Proximate and Ultimate cause)不同的觀點，對於一個科學結果的解讀是要非常小心的，尤其是各種因果關係之間的詮釋。在像生物這種尚未公理化的學科中，人們不可避免的必須脫離歸納法(induction)和演繹法(deduction)而使用溯因推理(abductive reasoning)。換句話說，一切的知識是建立的觀察而非邏輯公設，因此不存在所謂的真理，只有最好的解釋。然而“最好的解釋”本身是非常主觀的，話語權尤其會掌握在領域專家手中。話說回到近因與遠因，無論定義為何，根本上兩者都參雜了人的主觀意識。生物中的因果關係以及究極意義，是不是無法達到客觀上的共識？
生物學中的知識、理解、理論是什麼？
前面提到的這些例子和觀點，最終其實只是為了醞釀出Mayr在書中非常前面就想要傳達的概念，那就是生物學需要一套和物理(甚至所謂的傳統科學)不一樣的方法和哲學。還記得在讀書會的前幾週，我總是持著相反的意見，認為Mayr會這樣覺得是因為他懂的物理不夠多。如今，我還是不知道Mayr到底懂不懂物理，不過很肯定的是，我之前對生物的認識實在太淺薄了。
於是在這邊我想要紀錄一下我心境上的轉換，希望能夠帶給非生物背景的人作為一些借鏡，同時也讓生物學家(例如我室友)可以更知道一般受物理和數學訓練的學生通常會有什麼樣子的偏見。
科學哲學：生物學家和物理學家之間的誤解
我在大學的時候學過一些基礎的科學哲學，不外乎就是邏輯實證主義(logical positivism)、Kuhn的典範轉移(paradigm shift)以及Popper的否定論(falsification)。年幼無知的我很理所當然的把這些視為科學的公設，直到現在比較有思辨能力後，在受到This is Biology的啟發才重新發現科學哲學的廣闊與無邊。
Mayr在書中討論科學哲學的段落一開頭就說，這些不同流派的思想基本上都還是以物理學(甚至是理論物理學)為中心，並不見得那麼適用在生物學。而我覺得這之間的區隔，可以用一句演化生物學家Stephen Jay Gould一篇有名文章的標題看出來：『演化是事實和理論(Evolution as fact and theory)』。注意到這邊Gould沒有說演化是真實(reality)或真理(truth)，而以我對理論物理的粗淺認識，他們追尋的就恰恰是這兩者，這可以從一本我很喜歡由去年諾貝爾物理學獎得主Roger Penrose寫的書的書名『通往真實的道路(The Road to Reality)』看出來。
[...] facts and theories are different things, not rungs in a hierarchy of increasing certainty. Facts are the world's data. Theories are structures of ideas that explain and interpret facts. Facts do not go away when scientists debate rival theories to explain them. Einstein's theory of gravitation replaced Newton's, but apples did not suspend themselves in mid-air, pending the outcome. [...] Moreover, "fact" does not mean "absolute certainty." The final proofs of logic and mathematics flow deductively from stated premises and achieve certainty only because they are not about the empirical world. [...] In science, "fact" can only mean "confirmed to such a degree that it would be perverse to withhold provisional assent." I suppose that apples might start to rise tomorrow, but the possibility does not merit equal time in physics classrooms.
[...] 事實和理論是不一樣的東西，是無法比較誰比誰更為肯定。事實是這個世界的資料，理論則是解讀事實的一些想法和概念。當科學家在爭論對立的理論哪個比較能解釋某個事實時，事實是並不會跑走或改變。當愛因斯坦的重力論取代了牛頓時，蘋果並沒有因此停在半空中等待結果。 [...] "事實"的意思並不是"絕對的肯定"，當一個數學邏輯的證明從起始的假設，演繹地流動到最終的結論時，這樣無瑕的成就完全是因為它不是關於現實的世界。 [...] 在科學中，"事實"只能是代表"被確認到了連反對都看起來像是故意找碴那樣的程度"。蘋果的確有可能在明天就變成往上升起，不過這樣的可能性並不值得讓我們花時間在物理課堂中花時間討論。
Evolution as fact and theory by Stephen Jay Gould.
如果要用更近代一點的科學哲學觀念來剖析其在物理學和生物學的異同，我會說前者更傾向於科學實在論(scientific realism)而後者則是工具主義(instrumentalism)。簡單來說，科學實在論的中心思想是相信”理想理論(ideal theory)”的存在，並且主張科學研究的目標就是要往理想的理論前進。而工具主義則是持相反的意見，認為科學理論是個幫助我們理解和認識世界的工具，應著重於解釋和預測觀測到的現象。
在這邊我極度的省略了對於各種科學哲學流派嚴謹的討論，主要目的只是希望給讀者帶來一個種子，在未來可以自行繼續探索(Stanford的哲學百科全書是個不錯的起點)。同時一個很重要的觀念，科學哲學終究是個幫助我們理清楚科學研究的本質與目標，這既不是終點也沒有確切的答案，每個人都可以有不同的喜好，甚至同一個人對於不同的學科和子領域也可以有不一樣的信念。能夠多理解不一樣的觀點，除了充實自己的思想架構之外，更是能夠在未來與不同領域的人接觸時，更體會對方的思考方式。
數學在生物學中的角色與可能？
身為一個理論電腦科學家以及業餘的數學和理論物理愛好者，還是對數學以及形式上的美有很大的追求(和需求)。然而諸如前面討論到的，種種生物學面對的困難不禁讓人懷疑，數學真的也可以在生物學中達到如在物理學中那樣的成就嗎？最近看了一篇arxiv上的文章“A mathematician’s view of the unreasonable ineffectiveness of mathematics in biology”，作者透過對於著名跨領域到生物的數學家Israel Gelfand的觀察，提出了許多精闢的觀察和故事，蠻值得一個輕鬆的閱讀。
我個人最主要的看法是，現有的數學是很受到物理的影響，許多分枝都是對應到一些相關的物理子領域。相對來講，幾乎沒有什麼新的數學是受到生物啟發誕生的。這並不是說生物缺乏數學的可能性，而是現有的數學也許還不夠，需要有人替生物學創造出新的數學。
而什麼樣子的數學可能適合生物呢？現在生物物理學家或是生物數學家通常使用的是動力系統(dynamical systems)、微分方程(differential equations)或一些控制理論(control theory)、博弈論(game theory)，我認為其中非常缺乏了“演算法(algorithm)”的元素。在這邊我指的是更廣義的演算法，像是到了軟體工程的層次，有不同的子程式組成一個巨大的程式。這樣子用演算法/軟體工程的角度來理解生物系統，不但更接近邏輯運算而因此方便人類理解思考，同時也比前述的傳統數學方法更能夠處理特例、複雜的運算。現今的計算生物學(computational biology)可以說就是使用這樣的方法，只不過目前大多還是停留在寫程式跑模擬的階段，還尚未有很乾淨漂亮的數學語言可以做更抽象的分析。
也許一個可能的未來方向是試著如同Turing給了計算(computation)一個完善的數學根基一樣，在一些生物的子領域提出新的數學語言？最近理論電腦科學界的兩位Blum大佬提出了Conscious Turing Machine的概念，似乎就是個將演算法思維應用在接近生物領域的一個好例子？在接下的寒假，我預計要開一個mini-course關於計算在數學、物理和生物之間概念上的異同，希望屆時可以好好思考探索這個方向！
跨領域的現實、包容與理解、下一步
除了This is Biology的讀書會之外，在過去的一年半之間，我和Brabeeba也經營了一個跨領域的讀書會(When neuroscience meets CS, math, and physics)，讓我徹底地體會到了跨領域交流的困難是雙向的：除了自己本身需要學習更多、更站在對方角度思考之外，也必須要建立在於對方感興趣展開一段對話。這也讓我覺得，如果長期要做跨領域研究的方向，那麼勢必要先在不同的領域都紮下根基，理解各自的審美觀，累積一定的專業能力，甚至獲得一定程度領域內的認可。換句話說，就是需要在各個領域都達到基本研究生以上的能力吧！
意會到這樣的現實，初期的確令我有點小小沮喪，不過同時也感到非常興奮，非常期待五年十年後自己在各個感興趣的領域種下的種子漸漸冒出枝枒、開花。在這條有趣但充滿挑戰的孤獨之路上，也期許自己勿忘要包容與理解不同學科的多樣性和差異，有耐心和毅力地一步一步走下去。
(感謝Brabeeba Wang和Wei-Ping Chan對於文章的許多好建議！)
