Blog (English Version)
A place to record my feeling, my thought, my exploration, and my growth. Most of the posts here are translated with the help of ChatGPT. Click here to go back to the Mandarin webpage.
128th Statistical Mechanics Conference
19 May 2025(中文版原文連結)
(Translated from the Mandarin version with the help of GPT-4o)
It’s been nearly five or six years since I started mingling with physicists. I still remember how, in the early days, reading physics papers felt like trying to see through fogged glass—I often couldn’t grasp the narrative logic or structure, and I was frequently confused by the very different styles of mathematical symbols and how the formulas were used. These days, however, attending physics department talks or reading textbooks and papers feels as comfortable and enjoyable as reading math—almost a form of relaxation. I’ve even started getting comments from old CS friends saying my thinking and writing are becoming “too physics-like.” But there’s still one thing I hadn’t done until now: attending a physics academic conference.
Unlike in CS, where conferences are the main venue for academic publishing, the physics community primarily publishes through journals. That means there’s less pressure to attend conferences regularly unless you’re invited or want to promote your work. This time, however, my advisor was giving a talk at a statistical mechanics conference held at nearby Rutgers University. Since it was just a train ride away, and the conference was small (offering more chances for in-depth interactions), I decided to tag along for what became my very first physics academic meeting.
When I first saw on the conference website that it was the “128th meeting,” I thought it had been running for over a century. Later I found out it’s held twice a year—so it’s been going on for 64 years, still making it probably the longest-running conference I’ve ever attended (even top theoretical CS conferences like STOC and FOCS are only around 50–60 years old). Most impressive of all: this 128-time conference has been organized continuously since the first one by the same professor, Joel Lebowitz. Seeing him sitting in the front row of the lecture hall, attentively listening to each talk with his hearing aids on, was genuinely moving—a testament to his enduring academic passion.
This year’s conference honored three senior scholars: David Nelson, Stefano Olla, and Sara Solla. Each has made foundational and pioneering contributions in very different areas (condensed matter/biophysics, mathematical physics, theoretical/computational neuroscience), all through the lens of statistical mechanics. Over the three-day conference, every speaker was someone influenced by one of them—former collaborators, past students, etc. Because the honorees came from such different fields, the talks naturally clustered into three distinct groups. After a 25-minute talk about rat brain research, you might suddenly hear a story about discovering quasicrystals—like moving through a sauna, cold plunge, and steam room in sequence. Pure bliss.
Interestingly, it wasn’t just the topics that differed—the presentation styles and energy of the speakers also clearly fell into three groups. Most of the time, you could guess a speaker’s field just by hearing a few sentences. This reminded me of a conversation a few weeks ago with my friend J, about the difficulties of interdisciplinary research. We both agreed: the hardest part is learning the “culture” of different fields—the way people interact, communicate, and what they expect from each other. Compared to that, the domain-specific knowledge is relatively easy to acquire.
This cultural distinction was particularly evident during the laudation sessions—arguably the emotional highlight of the conference—which celebrated the three honorees in very different ways.
David Nelson’s laudation was given by his famous student Subir Sachdev, who delivered what could only be described as a dreamlike career retrospective. He went through Nelson’s seminal contributions from his student days onward—each paper founding a subfield, each theory later confirmed by experiment. Nelson has trained countless students, all of whom spoke glowingly of his mentorship—his deep knowledge, his rigor, and his uncanny ability to spot new problems. One student remarked that, now that she advises students of her own, she often wonders how David would guide them. That, to me, is one of the highest compliments you can give a mentor. The final slide—a five-generation academic “family photo”—nearly brought tears to my eyes.
Stefano Olla’s laudation, delivered by a longtime collaborator, focused on several of Olla’s most important papers. What stood out was the time devoted to explaining formal mathematical definitions and theorems in detail. I eventually couldn’t keep up, but the speaker’s sincerity and love for their field shone through. At the end, the presenter wanted to describe Olla’s character outside of his research. After a few seconds of thought, he gave what might be the most “mathematical” compliment I’ve ever heard: “Stefano is a good person.”
Sara Solla’s session, by contrast, felt like it took place in an entirely different world. Five or six computational neuroscientists acted out skits to portray symptoms of different psychiatric disorders, using them to narrate Solla’s various research phases. They also spoke about her community-building efforts, especially how her presence and charisma at summer schools influenced generations of computational neuroscientists. Each speaker had their own unique flair—some acted like they were on stage, others read formally from a script, and some delivered heartfelt tributes that felt like love letters. Even within this already interdisciplinary conference, neuroscience proved to be a world of its own, full of diverse subfields and styles.
The Challenges of Interdisciplinary Work?
Ever since I stumbled into interdisciplinary research, I’ve had many new realizations over time. At first, it felt like being in a buffet—constantly drawn in by the novelty and variety of different problems. As I accumulated more knowledge, I began to appreciate how the way we ask and answer questions can vary drastically between fields, leading to a deeper admiration for truly innovative work in each domain. Once I started doing research at the frontiers and had to explain it to experts from different backgrounds, I finally understood the importance of cultural literacy. Even if a project blends A, B, and C disciplines, when it comes time to write or present, you must adapt to your audience—not just present it in what you think is the “best” way.
In interdisciplinary research, it’s nearly impossible to fully address all A, B, and C fields simultaneously. After all, very few readers are fluent in all of them. At some point, you may have to choose—perhaps focusing on connecting just A and B. This made me think of immigrants and international students: learning multiple languages isn’t the hardest part. The real challenge lies in the identity struggles that arise from navigating between cultural worlds—those quiet moments of doubt that creep in at night.
Now that I’m no longer a student, I’ve started to appreciate the freedom I had to explore back then. As I settle into the cocoon stage of a postdoc—where exploration starts giving way to professional crystallization—I find myself enjoying research more deeply, taking on more responsibilities, but also beginning to ask: what kind of identity do I want to define for my future?
My First Post Doc Year
25 Dec 2024(中文版原文連結)
(Translated from the Mandarin version with the help of GPT-4o)
It feels like time has never passed so quickly in my life. It seems like just recently, my friend J and I went to see last year’s Rockefeller Christmas tree, and in the blink of an eye, households have once again put up their Christmas decorations. The light snowfall a few days ago has also added a bit more festive atmosphere compared to the same time last year.
Since graduating last year, I started a postdoctoral position in computational neuroscience at the Flatiron Institute under the Simons Foundation in New York. Although I am still in academia, and I had already interned here during the summer of 2022, looking back at this journey over the past year, I realize that the shift in field and role has unconsciously taken a lot of time and effort to adjust and adapt. Gradually, I started practicing piano less, hardly exercised, and spending all day coding and making figures drained my motivation to learn new things and write.
Switching fields feels like compressing four to five years of foundational training into a single year, while interdisciplinary research feels like learning two to three new languages simultaneously. The loneliness and self-doubt of forging a new path add to the mental challenge. Living in an era of paradigm shifts and widespread restlessness, I have often found myself suddenly realizing that I have spent too much time on trivial matters or being tempted to take shortcuts out of laziness.
However, there have also been many exhilarating moments—perhaps even more than I expected. Every time an experimental simulation matches my predictions, when I suddenly gain a new understanding of a derived equation, when I see students making small progress, when experimental collaborators discover interesting results using our methods and programs, or even when I stumble upon an insightful talk, an interesting paper, or gain new ideas through discussions with collaborators—it all makes the effort feel worthwhile.
Time Management
I still remember back in high school, when preparing for entrance exams, I would meticulously plan my study schedule in one-hour blocks before heading to the library with friends on weekends. I would even specify which pages of textbooks to read and how many practice problems to complete. Looking back, what amazes me most is that I usually managed to stick to the schedule and complete everything I had planned.
Of course, this habit gradually faded in college, especially after I started doing research. I shifted to the other extreme—relying on my intuition to decide what to work on at any given moment. Looking back, I have no idea how I managed to juggle multiple projects. Sometimes, I would get so absorbed in solving a small puzzle that an entire afternoon would pass. I still remember wondering during my PhD why my friend W often needed to watch some videos before starting work. He would always say, “You’ll understand one day.”
Now, I’m not sure if it’s due to aging or a change in my work nature (from abstract logical reasoning to intensive coding and visualization), but W’s words have proven prophetic. I often find myself sitting in front of my computer, wanting to start working but struggling to get into the flow. I need a distraction—eating something, watching a video or the news—before I can begin. The scary part is that once I enter work mode, I also find it hard to detach, only leaving the computer reluctantly when my legs or back go numb. This sensation isn’t unfamiliar, but in the past, I could carry problems in my head while walking or biking; now, my mind is clear, but my hands can’t keep up with coding.
On another note, since I started learning the piano in 2020, even though I’m still not very skilled, I can clearly feel the improvements from practicing for over an hour daily—better finger independence and strength, heightened sensitivity to sound, faster sight-reading, and much more room for growth. A few years ago, I could never have imagined playing like this.
These small, daily accumulations yield visible changes even over short periods. When learning a new (not overly difficult) piece, if I dedicate ten hours to practice, spreading it over a month with 20-minute daily sessions, I can usually play through it reasonably well, even if not at performance level. But if I try to cram all ten hours into a single day—not even considering the risk of hand injuries—it would be a struggle to get through half of the piece. On the other hand, if I only practiced five minutes daily for four months, I doubt I’d achieve the same results as the 20-minute daily approach.
Reflecting on these two observations about time management—when to start and stop work sessions and the cumulative effect of daily habits—I realize I need to rebuild my sense of time to live more efficiently and with better quality. My intuition about time is too constrained by its apparent one-dimensional structure, like a straight river flowing steadily forward. Immersed in it, I can only see the scenery around me, at best trying to peer ahead occasionally.
But anyone who has studied signal analysis knows that analyzing a time series usually starts with Fourier analysis, which, simply put, transforms the time axis into frequency bands for analysis. Looking at a weekly schedule from a time-based perspective feels like a chronological log: “Monday: bagel for breakfast, one-on-one meeting with my advisor at noon. Tuesday: a free day to focus on research. Wednesday: meetings with students, plus an evening seminar to attend…” This approach is great for tracking specific tasks, but when things pile up or scale increases, it’s easy to lose sight of the bigger picture.
Thinking about time from a frequency perspective, however, changes the question from “What tasks must I complete today?” to “How much time should I spend working today?” Instead of “Read 30 books this year,” it becomes “Read for 20 minutes during my subway commute on weekdays and for two hours one weekend afternoon.” Instead of “Publish X papers before my postdoc ends,” it turns into “Allocate a certain percentage of my time each week to different projects.”
Mental Stability
We live in an era of widespread anxiety, where rapid information dissemination exposes us to an unprecedented flood of data. In hunter-gatherer societies, people only needed to know a few dozen or hundred individuals in their tribe. Now, we are bombarded with news and social media, and our brains—which evolved for a much smaller scale of social interaction—struggle to distinguish which information is truly relevant to our lives.
Many of our emotional fluctuations and anxieties stem from misprocessing information. If we see different friends posting vacation photos every day, our brains might mistakenly group them together, creating the illusion that “everyone is always traveling except me, stuck working overtime.” In reality, those friends might only take one trip a year. Similar distortions happen when seeing “Yet another classmate published a paper,” “Someone else had a fancy dinner,” or “That person’s stocks went up again.”
At the same time, the overwhelming amount of information we must process has ironically reduced and rushed human communication. In academia, for instance, it may seem like per capita productivity has skyrocketed compared to a decade or a century ago, but despite technological advances reducing administrative burdens, people now have fewer opportunities for deep thinking and meaningful discussions. The lack of such dialogue leads to asymmetrical information (or in trendy terms, misaligned granularity), triggering a chain reaction of uncertainties and, ultimately, anxiety.
During my studies, perhaps because I was in a familiar field with shared communication styles, I maintained a stable mindset with little anxiety. I used to think mental stability was a form of soft skill—a matter of willpower and discipline. Maybe my baseball team training as a child helped me with this.
Now, looking back at my first postdoc year, I realize that sheer willpower is merely a necessary condition. The real culprits behind mental instability are information gaps, ineffective communication, and misplaced expectations. Especially given the differences in work styles and thought structures across fields, misunderstandings and misaligned expectations can lead to avoidable negativity. Yet, every time I sit down with my advisor or collaborators for a proper conversation, the clouds part, and my worries dissipate.
Mental stability is more crucial than ever in today’s fast-paced world. The root cause of instability isn’t necessarily weak willpower; it often lies in the poor handling of excessive information. My goal moving forward is to manage information better, establish good communication habits, and foster a stable mindset for myself and those around me.
What Does an Ideal Day Look Like?
Maybe it’s the magic of New York, but this past year has felt chaotic, making me lose sight of my ideal day. This Christmas break, cutting my usual 12-hour workdays down to 2–4 hours, practicing piano seriously again, writing and organizing my thoughts, watching movies, reading books, and reviving my sourdough starter—I’ll bake my first loaf in over six months tomorrow. Maybe it’s time to dust off my long-forgotten running shoes too?
First visit to Westminster Abbey
09 Sep 2023(中文版原文連結)
(Translated from the Mandarin version with the help of GPT-4)
In early September, London experienced its last heatwave of the year (or so we hoped). After a hurried breakfast, with excitement akin to meeting an online friend I’ve chatted with for years, I braved the blazing sun to visit Westminster Abbey, a place I’ve passed by countless times. Though I couldn’t literally meet these great figures I’ve admired for years, just as in conversations where we often understand and interpret words through our own imagination, I was eagerly looking forward to having a heartfelt “chat” with a few esteemed scientists.
No sooner had I cooled down and wiped away my sweat than I saw Darwin, standing right at the entrance to the main hall, just around the corner. Watching the steady stream of visitors passing by, some pausing to exclaim, “Oh, that’s the man who came up with the theory of evolution!” he seemed somewhat out of place. I quickly found a quiet spot nearby and stood there, smiling softly and observing.
Our eyes met, and I gave a slight nod. Suddenly, the setting felt like an academic conference. Seizing the opportunity, I quickly introduced myself and expressed my admiration for Darwin. Although I wasn’t entirely sure if academics back then addressed each other by their first names, I decided to play it safe and referred to him as “Professor.” Noticing his slightly puzzled expression, I felt a twinge of anxiety, wondering if I had said something amiss.
The air grew still for a few seconds before Darwin replied with a thick British accent, “I must admit I’m unfamiliar with these terms ‘computer’ and ‘neuroscience’ that you mention. However, since you’ve expressed an admiration for my work, perhaps you could explain why you appreciate it and how it relates to your research?”
I mentally kicked myself, realizing that I had overlooked the fact that both computer science and neuroscience emerged and matured in the 20th century. I couldn’t simply assume he was familiar with these topics. “I apologize for the oversight,” I replied, “If you’re interested, I’d be happy to explain the concepts of computers and neuroscience to you in more detail later.”
I nervously swallowed, “Your theory of evolution is one of the few I’ve encountered that elegantly links top-down functional levels with bottom-up mechanical levels.” Oh no, I thought, realizing I’d forgotten that he might not be aware of molecular biology and the modern interpretation of the theory of evolution. But then again, who knows? Perhaps he had foreseen all of these developments. “I particularly admire the concept of natural selection. It doesn’t optimize certain equations like general physical principles do. This open-ended mathematical principle feels like the key to understanding life, intelligence, and consciousness. While I don’t have a concrete theoretical framework yet, I hope to find some embryonic forms in the next thirty years…”
“Mm, I didn’t grasp everything you mentioned,” Darwin said, adjusting his beard, “but remember that the theory of evolution wasn’t solely my work. Don’t forget Wallace; he independently came up with the same theory at the same time.”
“Absolutely, sir. I wanted to mention how much I admire the camaraderie between you and Wallace. I wish modern academia could learn from you two instead of being embroiled in endless power struggles and politics,” I lamented, feeling frustrated that my thoughts were so scattered during our conversation.
“Perhaps that too is a process of social evolution,” Darwin remarked, his eyes clear and devoid of judgment.
Gradually, the expressions on our faces shifted to polite smiles. Sometimes, in such crowded situations, it really is hard to engage in deep conversations. Glancing at the throng of people snapping photos, I realized I had inadvertently and excitedly positioned myself in the middle of the pathway. I quickly nodded my head in acknowledgement and slipped somewhat awkwardly out of the crowd.
Walking to the end of the corridor, I arrived at the expansive hall on the east side (CHECK). A magnificent monument stood opposite the famed Tomb of the Unknown Warrior in Westminster Abbey. I watched as a young man, dressed in worn military attire, was surrounded by a group of royally dressed monarchs, politicians, scientists, and the like. Meanwhile, countless visitors eagerly took selfies and even livestreamed the scene. I was curious about how he might describe his life and even more interested in understanding who he originally was. However, the never-ending stream of visitors meant I had to content myself with peeking from a corner.
“These modern folks are truly ungrateful,” I overheard one elderly gentleman behind me grumble. “If not for the efforts and sacrifices of important people like us, there wouldn’t be the peace and prosperity we see today. They come here and don’t even bother speaking to us, choosing instead to crowd around that upstart. It’s utterly maddening.”
“Well, it’s not entirely like that,” another voice countered, sounding more measured. “Just as we wouldn’t have been able to achieve what we did without the thousands of nameless soldiers fighting for us, if not for this young man, who knows how many fewer people might visit Westminster Abbey each year!”
A vivid memory flashed through my mind: two elderly professors, discussing with similar tones about how to get the lab students to work diligently. The realization that history, across eras and fields, echoed similar sentiments and scenarios was almost chilling. Snapping back to reality, I blinked a few times. The two old gentlemen behind me must have noticed my eavesdropping, as an unexpected silence enveloped us, starkly contrasting with the surrounding commotion, rendering the moment almost surreal.
I nonchalantly continued walking, trying to merge with the flow of people. As I looked up, a sudden dizziness overtook me. The surrounding noise felt like it had been sucked into a vacuum, and the sight of so many eminent scientists standing in a row took my breath away. For a moment, I could empathize with fans who faint at the sight of their favorite celebrities.
But soon after, waves of guilt washed over me. Thinking of the many physics textbooks and papers I had intended to read but had left untouched, I was apprehensive about making eye contact with Professor Hawking or Dirac. I feared being exposed for my limited knowledge. Yet, pondering over Hawking radiation, the information paradox, the elegance of the Dirac equation, and the utility of Dirac notation and functions - all of which had influenced almost half of my doctoral studies - I silently expressed my admiration and gratitude to them, even as I remained wary of an inadvertent gaze meeting theirs.
Sir Isaac Newton, arguably the most significant figure in modern science, sat regally atop an ornate, large stone tomb. He seemed indifferent to the constant stream of visitors, having likely grown accustomed to the attention over centuries. For a few seconds, I grappled with my recognition – how could I not have known what Newton looked like? It might have been due to my lackluster attention to textbooks in high school. I found it hard to associate this handsome visage with the pioneering figure of modern science.
Over the years, as I delved deeper into the philosophy of science and engaged with various subfields of physics and more recent studies on complex systems, my appreciation and understanding of Newton’s groundbreaking contributions deepened. But at the same time, I grew increasingly curious about his views on the evolution of science. Would he approve of how far we’d come, building upon his foundational work? Or would he have critiques, given the visionary thinker he was? If only I could engage him in conversation and discover his insights.
I hesitated for a moment, reflecting on the depth of his words. “Sir Newton, you’ve laid the groundwork for how we’ve approached understanding the world for centuries. And while differential equations remain foundational, in the recent decades, we’ve started exploring alternative approaches to understanding complex systems. Computational models, simulations, and statistical methods are gaining prominence.”
I paused, trying to simplify the concept of computational complexity for this genius of the past. “Imagine a situation where the sheer number of variables and interactions are so high that solving differential equations becomes impractical. Instead, we use computers to simulate the system and try to draw insights from patterns and emergent behaviors. It’s a different way of ‘understanding’ the world, one that’s less about precise solutions and more about patterns and behaviors.”
Newton looked intrigued, his brow furrowed in thought. “Computers, you say? Machines that think? Intriguing! But it’s also a reminder that as the world evolves, so do our methods of understanding it.”
I nodded, deeply appreciative of his open-mindedness. “Indeed, Sir. It’s a testament to the ever-evolving nature of human inquiry.”
“Have you heard of ‘computer science’?” Seeing his puzzled expression, I quickly added, “You can think of a computer as a mechanized and discrete mathematical model, which can be used to attempt to describe the way humans think.”
“Moreover, nowadays, people can actually turn computers into real machines and perform complex calculations on them, such as solving differential equations!”
“Alright, I still don’t quite understand how this ‘computer’ relates to understanding the world.”
I didn’t expect Newton to give me another chance to explain. I quickly thought about how to convey it succinctly to him.
“Imagine if you had an infinite amount of time and plenty of paper and pen to do calculations.”
“I do have plenty of time now, but not enough paper and pens.” I wasn’t sure if Newton was making a joke or just murmuring to himself subconsciously.
“In that case, you can write down the system you’re interested in on paper in detail. Then, continuously use your favorite differential equations to calculate the next state of the system. In this way, even if you don’t solve a differential equation using a formula, you can still gradually compute the evolution of the system.”
“I tried doing that a few times in my days. But in the end, without a mathematical formula, how can one have a clear and beautiful understanding?” I felt he was quickly losing patience.
“Firstly, we now have machines that can compute these calculations very quickly, allowing you to see what the system will look like after a period of time. Secondly, it’s like doing an experiment, but this time we have access to every detail in the experiment. This allows us to potentially build abstract understandings on top of these intricate computational details.”
“That sounds somewhat interesting.” I sensed that Newton was probably just being polite. “However, it seems my fans are eager to take photos with me. Please excuse me for now.”
After years of training in hosting various academic conferences during my doctoral studies, I’ve become accustomed to the reactions of the experts. Until something concrete is produced, words are just words. This is also what attracts me to science. While good expression and presentation are certainly important, in the end, everyone looks at the real capability.
My lack of knowledge about British history meant that I spent most of my remaining time in Westminster Abbey superficially admiring the sculptures and architecture. When I came across great literary figures and musicians, I could only blend into the crowd, sneakily taking a few more photos, secretly envying Britain for having such a place to preserve and showcase its culture and history.
Stepping out of Westminster Abbey, the sun was still intense, and the crowd had grown. The nearby Big Ben was so dazzling that my steps were unconsciously drawn towards it. Watching tourists happily taking photos and a few children excitedly jumping around, I couldn’t help but feel elated. It’s great to visit London at this time. As I strolled along the River Thames, I silently thought to myself how fortunate it is to be an interdisciplinary computer scientist in this era.
Enlightenment, Knowledge, and Culture
03 Sep 2023(中文版原文連結)
(Translated from the Mandarin version with the help of GPT-4)
The British Museum, as the world’s first museum open to everyone, carries with it many historical burdens. The provenance of many of its collections cannot be separated from the colonialism and invasions of the British Empire at the time. Interestingly, in the food alley directly opposite the museum’s main entrance, over half of the restaurants serve foreign cuisine (especially a lot of Asian food). Among them, there’s a shop specializing in the famous British snack, Fish and Chips, which is surprisingly owned by a Korean!



A few months ago, I spent a day wandering through the Metropolitan Museum of Art in New York with my family. So, when I opened the map of the British Museum, at first glance, I thought it was a copy-paste. Especially after touring the Egyptian section, besides the many anonymous mummies (and mummified cats) and the Rosetta Stone, I wasn’t particularly impressed, given my limited exposure. After all, it’s not easy to encapsulate the 3,000-year history of ancient Egyptian culture. These world-renowned museums can only focus on specific dynasties. Each time I stepped out of an exhibit, I always felt puzzled, trying to decipher from which perspective I was viewing these fleeting moments of human history and civilization.
Before hunger struck, I decided to take a look at the smaller Age of Enlightenment exhibit. I still vividly remember how the Age of Enlightenment tortured me countless times in high school history classes. Among the 12 questions I got wrong in my college entrance exam, I’m pretty sure one was about the Age of Enlightenment. However, I at least knew that Britain played a leading role in the world at that time. This trip to the British Museum should be a good opportunity for me to reacquaint myself with this crucial period in modern human history!
The towering wooden bookshelves and display cabinets on both sides made me feel as if I was in an ancient library. The sparse number of visitors allowed me to finally set my own pace. The introductory plaque at the entrance briefly mentioned how people transitioned their methods of organizing knowledge during the Enlightenment. They moved from a medieval focus on religion and theology to methodologies of collection, classification, and organization. Such a straightforward explanation might have been quickly forgotten by my past self, but this time, it deeply intrigued me. As I slowly scanned the titles on the bookshelves, I wondered how anyone could read ten books about some obscure island’s travelogue. At the same time, I marveled at the determination and passion of those in the Age of Enlightenment who wrote countless thick volumes on a wide array of unique topics.
I conclude that there is no thing constantly observable in nature, which will not always bring some light with it, and lead us further with the knowledge of her ways of working.
- John Locke
Under the pampering of the modern education system, it wasn’t until the latter years of my PhD studies that I began to realize the difficulty of acquiring knowledge, and how many things that seemed obvious were anything but. It wasn’t until I started pushing the frontiers of human knowledge that I genuinely felt the bewilderment of choosing a direction in a vast ocean.
Now, in an age dominated by science, has the way we think and form knowledge once again hit a dead end? Firstly, we no longer have the courage and opportunity, like those in the Age of Enlightenment, to drop everything in our youth, travel the world, record our observations, and collect, synthesize, and deduce knowledge. Secondly, specific modes of thinking tightly grip our minds, causing us to subconsciously think in familiar, comfortable patterns. Faced with the dilution of information quality and the explosion of its quantity, do we need a new Age of Enlightenment? Or perhaps, unbeknownst to us, this movement has already quietly begun.
Ph.D.Defense Day
02 May 2023(中文版原文連結)
The day I started imagining five or six years ago has passed in the blink of an eye. Looking back now, many details are still vivid: the scent and heat from the oven early in the morning, eating bagels while watching a kart racing game with roommates and visiting friends, the aggressive Lyft driver, and the pain of push-ups. My Ph.D. defense day was like a long-planned stage play, everything almost went perfectly according to the script (except that the evening piano practice turned into a surprise party), it was so smooth that even I didn’t have the chance to stop for a few seconds, close my eyes and feel the beats in my heart. My roommate told me that the feeling of the day of Ph.D. defense was probably similar to a wedding day. Surrounded by friends who have been important to me over the years, I am truly a lucky person.
The six years of pursuing a Ph.D. were, of course, full of ups and downs. The six dishes at the reception after the defense talk metaphorically represented my mood each year (thanks to my undergrad friend K for helping to name them):
Seduced by sweetness (Panna cota): In the first year, I was like a child entering a candy store, wanting to taste everything I saw, absorbing all kinds of nutrients without any restraint.
Tasting the spices (Mysore pak): In the second year, I had many opportunities to attend conferences and workshops. I visited the west coast, UK, India (where I tasted delicious Mysore pak), and Switzerland, experiencing different research styles and environments.
Burnt off passion (Basque cheesecake): The breakout of pandemic in the third year indirectly led me to rethink about my research and question the methodology of theoretical CS. Also, my enthusiasm for the research topic at hand gradually diminished.
Expanding the boundary (Pizza art): In the fourth year, I began to systematically learn physics and neuroscience, expanding the boundaries of knowledge in research collaborations and reading groups, and rediscovering my passion for the pursuit of knowledge.
Kneading for perfection (Sourdough): In the fifth year, I tried to outline a medium-to-long-term research plan. My perfectionist spirit led me to be harshly critical of myself, wavering between different methodologies, trying to identify my own path.
Rediscovering the roots (Flies heads): In the sixth year, I made up my mind to step toward neuroscience. I also gradually realized the inevitable imperfections in different scientific methods, so I gradually let go of my criticism of theoretical CS and reconsidered the role computation could play.
At the surprise party in the evening, my good friend L asked if I had any regrets during my Ph.D. years. I responded without too much thinking and said that there would certainly be regrets, but how we perceive and accept them is subjective. Although it might sound like an evasive answer, this mentality is something I’ve slowly come to understand over the years. Of course, I regret that I didn’t achieve any of the three major goals I set for my Ph.D. (winning a best paper award, running the Boston Marathon, and giving a piano recital). I regret not cherishing many important beings around me, and I regret missing the opportunity to talk and take photos with many people on the day of my defense.
But just like what baseball has taught me, no matter how many times I have struck out before or how badly I was shouted by the coach, whenever I stand on the field, the ups and downs of the past are the nourishment for moving forward. I want to prepare myself to face any outcome with a smile and head held high.
Although time seems to pass continuously, there are moments when we can feel a strong division. After settling down for half a day, on the way to the piano room after the rain, the still cool evening glow seemed to look different. For many people, it was just an ordinary defense talk. For me, it was the fulfillment of many years of imagination, a summary of a winding exploratory journey, and the beginning of the next chapter in my life.
This is Biology
28 Nov 2021(中文版原文連結)
This September in Boston didn’t prolong the blazing heat of summer, but was full of the feeling of autumn. The wind kissed my face as I rode my bike down the bridge across the Charles River, making me feel like swimming in the cold water. The unusual cold September caused me to expect the early arrival of fall colors; however, the theory hike on the first weekend of October was not as colorful as I imagined. Unsurprisingly, theory and reality had a gap again!
I immediately started an exciting conversation about cross-disciplinary research between CS and Neuroscience with a new postdoc right after we started the hike on the White Dot trail of Mt. Monadnock. We talked a little bit about what problems we’ve been exploring respectively and then moved on to the difference between biology, CS, and Physics research. What kind of biology research is “closer to the reality”? How to justify a mathematical model being “biologically plausible”? During our intense debate, I suddenly saw the deep gulf (which is quite obvious, but I didn’t realize it before) between biologists and computer scientists: when talking about biological plausibility, the two parties are basically talking about totally different things!
As a CS-trained student, I understand that when we talk about biological plausibility, what we have in mind are “conditions” or “biological constraints” such as the local connectivity or the sparse activities of neurons. Then, the next step we usually do is using mathematical models to capture these conditions and start either abstract deductive analysis or computer simulation. However, for biologists, biological plausibility does not necessarily refer to a concrete checklist. It’s more like, after a huge amount of reading, experiments, and discussions, each of them gradually builds up their own intuition and worldview. As the experiments in biology contain so much noise and special cases, it’s nearly impossible to write down rigorous mathematical constraints and check them one by one objectively. So sometimes it’s actually quite interesting to see that biologists might not be as biologically plausible as computer scientists would imagine!
Cross-disciplinary research is challenging. Not only does one have to learn a lot of knowledge from other fields, but in my opinion, the most difficult part is to understand and appreciate the beauty in the other fields. I occasionally saw a book recommendation on Facebook for “This is Biology” by Ernst Mayr. Through this book, I finally got a chance to peek into the big picture of a great (evolutionary) biologist on biology.
A roller coaster ride of philosophy of biology
Originally, I had just thought to ask my roommate, an evolutionary biologist, to read and discuss This is Biology together. In the end, he enthusiastically invited friends from several different fields to form a reading group, and this began a roller coaster ride of building up my philosophy of biology.
The reason why I call this a roller coaster ride is that I was challenged and reshaped multiple times during these three months. Now that the ride has ended, I’m ready to bring my newly built values and beliefs to start my next journey. As there will be much more stimulus and growth in my future exploration in cross-disciplinary research, here I’m going to briefly take some notes on the enlightenments and changes This is Biology has brought to me.
The beauty and challenge in Biology
A physics friend used to joke with me that Biology is like collecting stamps, and its beauty is about the diversity and complexity in nature, while the job of biologists is to collect and record new discoveries. Relatively speaking, physics and math seem to delve deeper into the hidden symmetry and structure in nature and the abstract world. Implicitly, this shows some superiority of physics over biology. Indeed, physicists often have the confidence of having a deeper understanding of the world. In contrast, as biology is a relatively young field, many sub-fields are still in the stage of collecting more and more data and observations from experiments. But such a difference in their current development does not imply which field is easier and which is more difficult. At the frontier of a scientific field, as long as one keeps the curiosity to the unknown, the rigor of knowledge, and the persistence in quality, every step forward is incomparably important and irreplaceable.
I grew up in an environment with very little exposure to nature. Amidst the hustle and bustle of the city and the fantasy of the abstract (mathematical) world, I always had a hard time understanding and appreciating the beauty in biology. I still vividly remember the first time I talked about research with my roommate. When he told me he was going to spend a couple of years taking photos of butterfly specimens and writing programs to analyze the shape and color of their wings, I really didn’t understand why this counted as “doing research.” Why was he going to spend so much time on a single species out of millions? Why were six specimens for each type of butterfly sufficient? Why could they make any claim and result under seemingly weak correlations and evidence?
Indeed, from the perspectives of physics and math, biology may not be listed in the Hall of Fame for intellectual pursuit. But why do we compare biology with physics and math? Directly comparing these different disciplines is like comparing music and painting. Individuals’ preferences could influence rational thinking and discussion. In the end, the difference in “the sense of beauty” among different fields causes huge misunderstandings and even discriminations. So why not throw away our prejudices and try to revisit the beauty of biology?
From collecting stamps to playing jigsaw puzzle
Biodiversity is undoubtedly the main reason why people would think of biology as like collecting stamps. Currently, there are hundreds of sub-atomic atoms known in the world, but the number of butterfly species on Earth is nearly 20,000. If we think more carefully about how to classify organisms, we will notice that even properly defining what a species means is a highly non-trivial task. As biodiversity is so messy and dirty, where is its beautiful part? In some senses, biology indeed looks like collecting stamps since much work is spent on collecting, classifying, and processing data. So is this data collection process the beauty of biodiversity? To me, such a “collecting stamps” stage is just the first step of appreciating biodiversity. The real exciting part of biologists’ job is to figure out the underlying pattern and difference among the huge amount of noisy data.
Thus, in my opinion, the beauty of biology is more in the stage after collecting stamps. And I call it the “playing jigsaw puzzle” stage. At this stage, people need to put the messy data points (i.e., pieces of a jigsaw puzzle) with certain correlations together. Moreover, one should not be interfered by superficial similarities (e.g., in the jigsaw puzzle below, different orange pieces might come from different orange cats!). Even worse, most of the time, it is impossible to collect enough pieces, and hence biologists often have to figure out something insightful without seeing the whole picture.
As a comparison, physics and mathematics are more like playing board games or strategy games where one of the main challenges is to walk through a huge maze with a small number of local choices/rules and huge global possibilities.
So in order to build up a sense of beauty for appreciating biology, I think we should temporarily loosen our insistence of logical perfection (in the sense of having a theory from first principles) and focus more on how to get something useful and interesting out from the huge and messy experimental data. If one doesn’t appreciate such kinds of beauty, then it might also be hard to have a deeper appreciation in some of the modern developments/research in biology. But of course, I’m not here to ask every reader to change themselves and start to like biology after reading this article. I guess the point is more about discussing the intrinsic differences between biology and physics (also math and other natural sciences). In the end, I really hope people from different fields can have fewer misunderstandings and discriminations towards each other. And if they have more time, they can even learn a little about the challenges and hopes in other fields.
Anyway, as I started to appreciate more of the beauty of playing jigsaw puzzle in biology, I realized much more exciting and cute aspects to explore. Here, I would like to share three recent revelations I had: the beauty of diversity, the beauty of the individual, and the beauty of the experiment.
The beauty of diversity: I vividly recall when I first met my roommate, I truly didn't understand why he was so excited about seeing a new ant species (to be honest, I still haven't fully grasped it...). In retrospect, my previous pursuit of beauty was more about abstractions, forms, and symmetries, while the beauty of biodiversity is almost on the other side of the coin. Particularly, it's often about concrete objects, real practices, and special cases. Nevertheless, although the two senses of beauty are very different, they are not necessarily conflicting with each other. Each person would have a different inclination toward these two types of beauty due to their family and education. And it is totally fine for a person to stick to the beauty that they find more comfortable with. But after opening up their eyes to the other type of beauty, the whole world will start to look more colorful. In my case, after having more and more appreciation for the beauty of biodiversity, every flower and tree on the street began to tell their stories to me. I also got a wider range of feelings on the surroundings and knowledge, and sometimes they could even bring me inspirations and joys.
The beauty of individual: Every organism is a unique existence in the world, unlike every hydrogen atom that basically looks exactly the same in the experiment. While biologists are working on finding patterns within biodiversity, the discovery of patterns could also bring new understandings of an individual through their differences. By building up theories in biology, we not only aim to figure out the governing rules behind reality but also try to find our own new perspectives and angles to comprehend the subtle beauty of the individual.
The beauty of experiment: In physics, people verify theoretical models through extremely precise experiments. In contrast, experiments in biology often cannot achieve such precision, and hence people often have to make claims from limited data and resources. For example, in the butterfly research of my roommate, he uses only six individuals for each species (and he told me this is the highest standard). This is not because they don't want or they cannot use a hundred individuals for each species. It is simply infeasible for them to conduct such a huge experiment under limited time and hands. Such reality constraints (e.g., the number of data points, noise in the data, etc.) are like the logical rules in mathematics. Biologists really need to struggle among these constraints and design meaningful experiments. I would say this might not be much easier than a mathematician walking through the labyrinth of axioms.
Let me give two examples of decision-making experiments in neuroscience to help readers appreciate the beauty behind experimental design.
First, some background information: in the study of decision-making, neuroscientists aim to identify network structures that can be mapped to decision-making mechanisms. A major challenge is to rule out as many alternatives as possible so that experimental findings can only be explained by the proposed theoretical model. Therefore, in addition to designing devices, researchers must also design animal behavior tasks and interpretations of various possible outcomes.
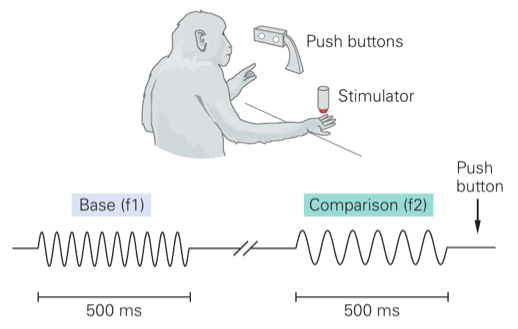
The first experiment is related to the somatosensory system. In this experiment, the fingers of a monkey are stimulated by a 20Hz stimulus for 500ms. Afterward, another stimulus with a different frequency is presented, and the monkey must decide whether the frequency of the second stimulus is higher or lower than that of the first stimulus.
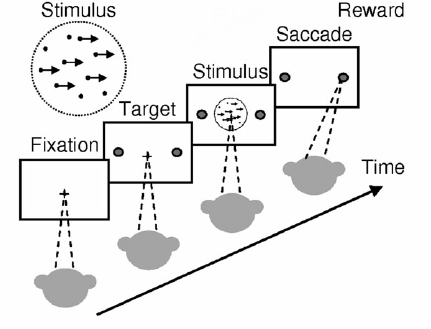
The second experiment is related to the visual system. In this experiment, a monkey first fixates on the central fixation spot of a screen (usually a cross) while dots are presented and move either from left to right or from right to left. Then, the monkey must decide whether the dots are moving toward the left or toward the right. Furthermore, a fraction of the dots move randomly to adjust the difficulty of the decision-making task.
Both of the above experiments are classic in the literature of decision-making. However, is one of them better than the other? If you think carefully, you will notice a big issue in the first experiment: there is a time gap between the two stimuli, and hence the monkey has to "memorize" the first vibration and compare it with the second one afterward. Note that this additional requirement of memorization (implicitly) increases the complexity of the task and hence makes it harder for the experimentalists to dissect the specific network that is responsible for the decision task only.
As for the second experiment, it first bypasses the memory issue by presenting all the information simultaneously. Second, it provides an adjustable parameter on the fraction of randomly moving dots to enable a more quantitative study of the underlying mechanism. Finally, the initial fixation is like a "reboot" that makes sure the monkey starts from a similar initial condition in every trial.
Different challenges: the lack of symmetry, emergence properties, objective meanings
To further establish a sense of beauty in biology, one has to embrace and understand its challenges. Here, I’d like to emphasize the following three challenges of biology from my personal view: the lack of symmetry, emergence properties, and the existence of objective meanings.
The lack of symmetry: It's not an exaggeration to say that the great success of modern physics is established on top of the brilliant observations of symmetry and asymmetry of the physical world. Symmetries not only lead to rich mathematics but also restrict the search space and enable abstract analysis (recommended reading: The Unreasonable Effectiveness of Mathematics in Physics). However, the jungle of biology seriously lacks those diverse and beautiful (and analyzable) symmetries. In my opinion, this is the root of the challenges to building good theories in biology. Thus, most of the mathematical or computational models in biology are more or less like a "description" as opposed to a "model" for the underlying reality.
Emergence properties: The so-called *emergence property* in biology is conceptually very similar to the *chaotic phenomenon* in physics: a bunch of applications of simple rules induces complicated results. Personally, I like to use a theoretical CS concept to think about emergence properties: one-wayness, i.e., easy to compute/manipulate in the forward direction, but hard to revert back to the initial starting point. How does an embryo develop into a mature organism? How are genes mapped to phenotypes? How do neurons' activities form computation, intelligence, and consciousness? Emergence properties make mechanical modeling and understanding extremely challenging. Either we get a rough statistical understanding via macroscopic analysis or get some models that soon become too complicated to understand as well (e.g., using deep learning to build a model). Meanwhile, the *reduction method* that is commonly used in physics also often oversimplifies the emergence properties and cannot capture multiple aspects simultaneously. Perhaps we really need a new methodology/framework to the traditional physical and mathematical methods?
Objective meanings: People always like to endow meanings to whatever we see. I still vividly remember during my last trip to Antelope Canyon, besides being amazed by the extraordinary workmanship of mother nature, I was also impressed by the creativity of the local tour guide. Within a few steps, you would hear something like "Look! This is the shark from Finding Nemo!" (see the figure below). I believe no one will believe that mother nature purposefully sculpted a shark in Antelope Canyon. However, this also reminds us to be aware of our own inductive bias while trying to understand nature. This reminds me of the comparison of *proximate cause* and *ultimate cause* mentioned in the book. It is truly subtle to be clear on what type of explanation one is talking about, especially when it is about correlations and causations. In a non-axiomatized discipline like biology, people unavoidably have to learn how to move forward without induction and/or deduction. Most of the time, the main scientific method is then based on abductive reasoning. In other words, all the knowledge is built on top of observations instead of logical axioms. Thus, there's even no so-called ground truth. There's only a better explanation rather than the best explanation. Nonetheless, "a better explanation" itself is very subjective, and the voice is often controlled by those experts in the field. Perhaps it is impossible to achieve a fully objective consensus in biology?
What are the knowledge, understanding, and theory in biology?
All the above examples and perspectives are serving for a key message Mayr wanted to convey from the very beginning of the book: there’s a need of different/new set of methodology and philosophy of science for biology (because those have been dominated by physics). I still remember that I always disagree with this opinion of Mayr and thought that he didn’t know enough physics. But now, even though I still don’t know if Mayr really knew some physics or not, I do know that my previous understanding of biology was too shallow.
So here I’d like to record the transition of my mindset and hope to prevent the non-biologists reader from discriminating biology. Meanwhile, this can also be an opportunity for biologists (like my roommate) to have more senses on the common prejudice from students with physics and math background.
Philosophy of science: the misunderstandings between biologists and physicists
I learned a little basic philosophy of science during my undergrad. It was nothing more than logical positivism, Kuhn’s paradigm shift, Popper’s falsification, etc. As ignorant as a kid, I had been regarding these as the axioms of doing science for a very long time. Not until I had much more independent thinking in the past few years did I realize the abundance of philosophy of science.
In the first paragraph of the Philosophy of Science section in the book, Mayr pointed out that even though there are several schools of thought, they all still center around physics (especially theoretical physics) and might not be that suitable for biology. I think this difference can be perfectly explained by the title of a famous paper by evolutionary biologist Stephen Jay Gould: “Evolution as Fact and Theory.” Notice that Gould didn’t say that evolution is reality or truth, while these two are exactly what most theoretical physicists are looking for! For example, this mindset can be seen from the title of the book by Nobel Prize in Physics laureate Roger Penrose: “The Road to Reality.”
Using more modern concepts to analyze the comparison of physics and biology, I would say the former is more like scientific realism while the latter is closer to instrumentalism. Simply speaking, scientific realism believes in the existence of an “ideal theory” and advocates that the goal of scientific research is to move closer and closer to the ideal theory. However, instrumentalism takes the opposite opinion and believes that scientific theories are tools for us to understand the world. Hence, the focus should be on explaining and predicting real-world phenomena.
Of course, I oversimplify the serious comparison and discussion on the different branches of philosophy of science. My main aim here is to plant some seeds in the readers’ minds so that you all can explore and build up your philosophy of science (The Stanford Encyclopedia of Philosophy could be a good starting point). As a friendly reminder, it is important to keep in mind that the philosophy of science ultimately is still just an assistant to help us clarify the goal and essence of scientific research. It’s not the end, and there’s no correct answer for it. Everyone can have different preferences, and the same person can even have different philosophical beliefs in different disciplines or sub-disciplines. If one can understand more perspectives, then this not only enriches your thinking, but also helps you think from other’s angles when talking to someone from a different field.
The role and possibility of math in biology?
As a theoretical computer scientist, an amateur mathematician, and a hobby physicist, I still have a strong pursuit (and need) for math and the beauty of abstraction. However, all the challenges in biology we have discussed above hardly do not make me wonder the possibility of applying math in biology. Recently, I came across this arXiv paper, “A mathematician’s view of the unreasonable ineffectiveness of mathematics in biology,” which gives a pretty good exposition of my concern. The author provides lots of observations and stories centering around the famous mathematician Israel Gelfand (who worked on biology after being well-established in pure math). I recommend it as a casual and enjoyable read.
My personal view is the following: Mathematics has been highly influenced by physics, and many branches correspond to a certain sub-discipline in physics. On the contrary, there are very few examples of new mathematics that were inspired by biology. This does not say that biology lacks mathematical potential. Maybe current mathematics is not yet ready for biology. We need someone to create new mathematics for biology!
But what kind of mathematics could be suitable for biology? Common mathematical tools used by bio-physicists or mathematical biologists are dynamical systems, differential equations, control theory, game theory, etc. In my opinion, there is a lack of an algorithmic lens. Here, what I meant by algorithms is something more general than the Turing machine sense. I meant something at the level of a software engineer, where there are huge programs with multiple sub-programs and their sub-sub-programs. Using such an algorithmic/software engineering view to understand biological systems can not only provide an analytic/logical methodology but also give different levels and granularities of understandings. The current development of computational biology could be something that is closest to what I have in mind. But most of the work there is still in the stage of writing models and running simulations. There is still no clean mathematical language that enables abstract analysis.
The reality of cross-disciplinary research, sympathy and understanding, next step
Besides the reading group for This is Biology, I also have been running a cross-disciplinary reading group (When neuroscience meets CS, math, and physics) with Brabeeba. These experiences make me fully understand that the challenges of cross-disciplinary interactions are bi-directional: besides learning more from the other fields and thinking in their shoes, the conversation should also start from the basis of the other person being interested in learning what you can bring. I then realized that to do cross-disciplinary research in the long-term, one should not only have solid foundations in different disciplines but also build up a sense of beauty and/or even get recognized by these fields to some extent. Quantitatively speaking, one should arrive at the basic graduate student level in the other field!
After realizing the challenges in front of my cross-disciplinary agenda did make me a bit frustrated in the beginning, but now I feel super excited and am very looking forward to what I will get to in all the different directions I’m interested in. I hope that I won’t forget the importance of sympathizing and understanding the distinctions of different fields and persistently push forward this lonely but fascinating journey.
My Fourth Ph.D. Year
11 Aug 2021(中文版原文連結)
A sudden gust of wind came out of nowhere, blowing sweat into my eyes and almost making me burst into tears. No matter how hard I pedaled, the canoe was uncontrollably swaying like a snake. Looking at the two little islands beside me, I felt as though the canoe had not been moving forward but had been blown a few meters back by the wind. Just half an hour ago, we had decided to circle the second island of Graham Lake and see the eagle’s nest before going back. Suddenly, we were trapped in the middle of the lake by a mysterious windstorm. Even straining all the power from our bodies, we could barely maintain the balance of the canoe. The eagle hovering nearby seemed like an outsider watching our misery and laughing at us.
As most of the meetings this week had been canceled for STOC, my roommate, his wife, Brabeeba, and I took a long-awaited escape trip to the north. Like the quarantine had come all of a sudden, the reopening in the US was also surprisingly fast. Within a week or two, most people on the street no longer wore masks, and most indoor activities had resumed. It took me a few more days to adapt to the “new life” after seeing zero COVID cases in Cambridge in a row. Putting the mask away and showing the whole face in public had never been this awkward before, like the first time running without a shirt on. Not until I began to smile at the pedestrian did I realize that normal life was finally back! Oh, perhaps I should have said it’s the new start of the post-COVID life.
Nonetheless, the escape trip that had been planned to be relaxing was kicked off by the 4-hour lake-trapping misery. It might seem irrelevant to the topic of this article, but interestingly this unexpected interlude is strikingly similar to my 4-year Ph.D. journey so far. Starting with getting on the canoe, holding the paddle, and excitedly watching the magnificent lake view, then going through a slightly challenging but endurable voyage and arriving at the eagle nest told by the local people. Suddenly, the wind direction was switched, and the destination looked unapproachable. We kept adjusting the possible routes to go back but soon realized the theory had always lagged behind the real situation. Sometimes we were blown to a neighboring island, and within a blink, we were blown back to the eagle’s nest island again. Most of the time, we were basically circling around the same position. Seeing the sun rising and rising, I started to wonder if we could really safely go back to the shore. Luckily, I was not alone, and the cheering and collaboration between me and Brabeeba really made a difference. When the wind was strong, we tried to stabilize the canoe and made sure we were not moving backward by too much. When the wind was smaller, we turned on our turbo and dashed for as many meters as possible. When we were getting closer and closer to the shore, we suddenly realized how different the sense of distance on the water compared to what it really was. We always thought it was going to be the last five minutes of the journey and sadly realized the scenery in front of us did not really change afterward. The details of the destination finally became clear at the very last moment, and without any preparation in mind, we had already arrived at the shore.
The unexpected trap shattered the romantic illusion of living by a lake. While frantically consuming snacks in the wooden house to regain some energy, I vowed never to canoe again in my life and worried that the soreness of my muscles would ruin the rest of the vacation. However, after waking up to the birds’ songs the next morning and meditating by the lake, I couldn’t help but fall in love with the depth and spirit of nature. My muscles were not as tired as expected, and they seemed to ask where the next journey would be.
After four years of Ph.D. life, I feel like a little boy who just finished a voyage, tremblingly witnessing the majesty of the world. I still have doubts about my ability and perhaps some disappointment in the shallowness of my former self. My passion is no longer vigorous but increasingly rounded and steadfast. Where is the next journey? This will be an unstoppable question, and the certain response would be: I will keep moving forward and thriving.
Before the next journey, let me record and share some recent thoughts.
What have I done in the past year?
The pandemic has made daily life monotonous and time seems to pass by quickly. Compared to the growth and challenges of the past few years, this year feels like waiting for a feast to cook in an oven, wondering about the next dish.
As for learning, I am still not accustomed to online courses and often miss important parts. Seeing students leaving Zoom immediately after class makes me miss corridor discussions and debates in front of a blackboard. After serving as a teaching assistant for two semesters and a week of summer school, I feel like I’m missing something. I can no longer observe each student from the last row in the classroom and it’s even harder to take care of everyone during office hours. Before the pandemic, when the “flipped classroom” had started to become a trend, I thought online courses would gradually replace physical courses entirely. Not until the pandemic lockdown did I realize that real-world interactions with people are irreplaceable.
Despite this, these teaching experiences have been a great source of mental nourishment for me during the pandemic. Students’ curiosity and eagerness to learn have reminded me of the pure and original passion of studying theoretical computer science. Seeing students slowly grow and start to ask interesting questions gives me a sense of achievement and happiness that I cannot get from doing research. This makes me determined to pursue education and academics in parallel.
In terms of research, there have been several follow-up works on the two breakthrough directions from last year. However, time has flown by, and I suddenly realized that I am less excited about some of the research results I have obtained. Furthermore, I now spend much less time on my most interesting problems, let alone studying new knowledge and thinking about a long-term research agenda. Looking at the tiny amount of time left in my Ph.D. life, I have gone into another swamp of confusion, not knowing how to properly allocate my time.
There are perhaps two main ways of time allocation among the postdocs and Ph.D. students I’ve met. The first type is what I call the “greedy algorithm,” where one goes all in when there are research problems that are doable and solves every follow-up work. The second type is what I call the “idealist,” where one only spends time on his or her favorite problem(s) and does not care that much about the production and progress. Of course, most people are a mixture of the two types. But from my observation, most people who survive in the end are often those who adopt one of the extreme styles. The two styles are incomparable and give different contributions to scientific advancement. Certainly, academia needs both types of researchers, so the point is to identify which style (perhaps beyond these two) works best for you!
In addition to the above meta-level thinking in research direction and style, I’ve been pondering a lot about the essence of scientific research, the differences and similarities among fields, the weaknesses of us as humans, and these sorts of philosophical questions. Let me try to roughly summarize my fuzzy thoughts in the rest of this post.
The differences and similarities among scientific fields
Since I started studying and doing research in Physics and Neuroscience two years ago, I gradually realized that the methodology, goals, and philosophies in different fields could be very different, and sometimes even contradictory or conflicting. For example, in theoretical CS, research without solid and rigorous mathematical proof is nearly impossible to gain recognition from the field. However, people care much less about the relevance of results to the real world and practical applications. Sometimes TCS people might even say “a research being too practical is no longer doing theory”. As for theoretical physics, my superficial understanding suggests that the requirement for mathematical rigor is not absolute. A common research approach is to provide complete theoretical analysis in a simpler setting and use experiments or computer simulations to support more complicated but realistic situations. In theoretical neuroscience, even the most theoretical works I’ve ever seen still use “fuzzy math,” and the focus is usually on experimental designs and how well the theory/model explains observed phenomena.
I really like my friend Lisa’s way of visualizing the differences among scientific fields via “knowledge trees.” Mathematics and Physics are like holy giant trees, aggregating centuries of knowledge and having many sub-branches entangled with each other. Computer Science is like a binary tree, with explosive growth in recent years and many branches, but relatively few long branches like the trees of Mathematics and Physics. Biology is then like shrubbery, touching tremendous observations and questions but rarely having a unifying understanding among sub-fields.
Such differences partly stem from the development and evolution of each field and partly from the subject a field is studying. For computer scientists, thanks to the abstraction of Turing, we can purely work in a utopian realm where everything can be captured by beautiful math. But for physicists and neuroscientists, what they are facing is the complicated and mysterious nature. Consequently, it is much more challenging to mathematize, and sometimes I even doubt whether it is really possible for living science to encompass elegant mathematical theory like CS and Physics.
Recently, I have been participating in a reading group for the book This is Biology by Ernst Mayr, a giant in evolutionary biology. The book discusses the philosophy of biology, and my goal is to build up my own scientific picture and think about the possibility of theoretical and abstract study in living science! I will write a separate post on this very soon!
The importance of open-minded and communication
As a junior student and researcher in academia, it’s very difficult to understand the perspectives of other fields after just becoming accustomed to the methodology of one’s home field. Sometimes this difficulty arises purely due to a lack of understanding, for example, I still find it challenging to appreciate the importance of some breakthrough results in neuroscience even after reading neuroscience papers for two years. Other times it’s because of a different way of thinking, like how computer scientists are very used to thinking algorithmically while physicists and mathematicians place more emphasis on symmetry and harmony. If one tries to force another field to think like their field, it not only is likely to fail but could also be very offensive. So, to foster a healthier and more comfortable environment, it’s crucial to be open-minded. This doesn’t necessarily mean that one has to understand and appreciate other fields, the point is simply that there’s no single field that is superior to the others, and we should embrace the diversity in academia!
Let’s even first ignore cross-disciplinary research. Being receptive to the diverse research methodology/style is also very crucial even in our own little sub-field. In the past year, I went through a drama of offending my collaborators due to the different styles of doing research: I like to understand the high-level strategy of a mathematical proof before pinning down every step of details, while some people are more comfortable with understanding a proof line by line. These two styles are both common in theoretical CS, and two persons with different styles can even be a really good match. However, I previously thought everyone should default to my style, and hence made my collaborator with the second style have a very difficult time understanding what I’m explaining. Not until we got a chance to chat about this and tried to understand each other did we figure out a better way to collaborate.
From the language and methodology gap among scientific fields to the difference in personal styles, I realize one of the valuable but often overlooked merits of scientific research: communication. In the ideal situation, Science and traditional dogma are very different in the lack of authority, emphasis on verification, and open discussion. Though of course, this is quite idealistic, and reality (e.g., caused by competition) might disappoint me, the difference between Science and other failed Utopians is that it is, in principle, not a bad idea to improve one’s communication skills and acceptance of others.
However, when I discuss with friends about the role of communication in science, some might doubt its necessity. Their argument is that in order to make others understand and appreciate their research, they might sometimes have to sacrifice the core value or originality of their work. Some more radical arguments suggest that there’s no need to spend time writing papers, and good research should prove itself without being written properly. Firstly, I believe there’s no conflict between independence of thinking and the understandability of a work. Furthermore, it’s often the case that one gains a clearer and deeper understanding after writing the paper or explaining it to others. Secondly, in my opinion, one key difference between science and art is that science chases objectivity in its essence while art embraces diverse and subjective expositions. To achieve the ideal objectivity in science, communication then becomes a critical step, and in modern science, writing is one of the ways to do it (of course, it could be the case that in 50 years there will be a better way to communicate!).
Deep understanding vs. Clear understanding
I am not sure when I started having a stubborn pursuit of deep understanding. That is to say, no matter what I encountered, I unconsciously judged how deep a question is and looked down upon problems that I think are not deep enough. Such pursuit unwittingly affected my life, and I started to become very judgmental. I suddenly realized I had gone too far when some of my close friends and collaborators started to have no clue about what I’m talking about.
What is “deep”? Is there an objective measure to evaluate how deep a problem is? Is deep understanding a standard to evaluate how good scientific work is? After revisiting these fundamental questions, I realized that “being deep” is as subjective as something like “being interesting.” And sometimes, when used improperly, “being not deep” could be a very offensive term. Maybe my original intention was about the scientific spirit of chasing the truth. However, once this becomes a concrete measure, it could make me have my head in the clouds and even be a little cynical.
This is not to say that pursuing deep understanding is wrong. Rather, this is a term that requires more careful and humble usage. In the meantime, I found a nice proxy for deep understanding: pursuing “clear understanding.” Looking back to my school days when I got stuck in homework problems, felt frustrated doing research, or even encountered an infinite loop while handling daily chores, what’s the common theme among them? I think all of these situations more or less stem from not clearly understanding the underlying principles or processes. In daily life, we may not necessarily need to make everything clear. However, some problems might emerge (e.g., tax issues) if such laziness aggregates. And to deal with them, the best way is often to clearly figure out the underlying issue. Similar principles can apply to the scientific frontier as well: examining scientific breakthroughs, as some of them come from a burst of inspiration, while many originate from the process of clarifying an unsatisfactory old understanding. In other words, pursuing clear understanding is a realization of intellectual honesty, and perhaps an understanding would be deep once you understand it clearly enough!
Weakness of human being and ego, rationality and sensibility
Since I noticed my obsession with abstract thinking, I started having lots of discussions about “human” with my good friend Juspreet. As science brings the belief that “man can conquer nature (人定勝天)” and modern life becomes more mechanical, we unconsciously become more like rational machines/robots and forget that we are still human beings. Francis Bacon once said,
Nature, to be commanded, must be obeyed.
Francis Bacon, Novum Organum
Similarly, being human, we should humbly acknowledge our weaknesses or, in other words, our essence.
Juspreet made two observations about me: first, he noticed that I care a lot about others’ feelings (but this doesn’t mean that I’m good at observing people…) and am also easily affected by others’ behaviors. In an open and straightforward environment (e.g., the way Juspreet and I hang out or some professional collaborations), such a personality might not be a big deal because people are straightforward with each other and can solve potential problems immediately. However, in many occasions, being too straightforward might not be very welcomed. Many people tend to tolerate each other to maintain harmony on the surface and thus implicitly create some unexploded bombs. If one does not care that much about others’ feelings, these unexploded bombs might not cause too much damage. However, if one cares about others’ feelings but also likes to be straightforward, it is then very easy to get oneself into an awkward and torturing situation. In the past year, I have suffered from such personality both in life and in research collaborations.
Fortuitously, I recently reread a book that I bought a couple of years back: “The Righteous Mind: Why Good People Are Divided by Politics and Religion,” and this book surprisingly provides me many new angles to think about my personality. The author, Jonathan Haidt, is a moral/social psychologist, and this book (as well as some of his previous books) presents a brand-new framework to describe the tangle between rationality and sensibility (in the book corresponding to “intuition” and “emotion”): other than the rationality-dominance view from mainstream scientists and popular media, the author leans more towards David Hume’s idea of “rationality is the servant of emotion.” Using plenty of psychological experiments and even viewpoints from social science and evolutionary theory, Haidt brilliantly explains how our emotions affect our rational thinking and further result in conflicts on political or religious debates.
Similar concepts can be used to explain lots of unpleasant incidents and quarrels in life and research. If one harshly rejects others’ proof ideas, is that going to make people feel embarrassed? If one deletes all the contents written by collaborators, is that going to make people feel offended? If one is impatient to explain details to the other and does not try to understand the other’s lack of background, is that going to make people feel insulted? Most importantly, when these situations happen, it is of no use to explain how innocent one was. Because once the hurt on emotion has been made, it is subjective and the emotion needs to be taken care of before rational discussion.
This is then very related to Juspreet’s second observation: ego. Although I care a lot about others’ feelings and sometimes can understand why they have such reactions, in the meantime, I still find it difficult to accept people not using the way I think is better. In other words, rationally, I can understand people’s intentions, but emotionally, I cannot agree. This is exactly the difference between sympathy and empathy.
So, besides reading and communicating to understand others’ feelings, what I really need to improve is to lower the strong ego within me. I need to accept diversity from the bottom of my heart, which happens to be the great lesson I learned from biology and nature!
Epilogue
Not sure if I have been influenced by the pandemic or a novel I recently read, but I have started to look at research and daily life from different and new angles. Time flows silently but steadily, and the world is full of hustle and bustle, changing uncontrollably. Living in reality requires us to be strong and steadfast while also acknowledging the confusion and shout-outs that build up deep in our minds. To meet basic living requirements, to spend the seemingly boundless time, to release our inner voice and express ourselves, we sometimes get caught in a fast and deep swirl and lose our direction. What are your strengths and weaknesses? What style is suitable for you? What is most important to you? Perhaps, while peddling hard in a lake, it is worth stopping for a while to think about these questions.
The Glass Bead Game
14 May 2021(中文版原文連結)
It’s quite embarrassing to admit that I had never finished reading an English book (as well as an English paper…) from the first page to the end before this year. For textbooks, it might be understandable because either the professor could only cover at most half of the materials or I just use it as a reference for specific contents. As for novels or non-fiction, I always gave up halfway through and bought a Chinese translation because my English reading speed is way too slow. This worked pretty well before the pandemic as I went back to Taiwan every year and hence could easily get books in Chinese. However, since the never-ending pandemic started, my stock of Chinese books has run out, so I have no choice but to start reading English books, albeit slowly.
I’m not a person who reads a lot. On average, I read about 10 to 20 books per year, and every day I probably only read for 30 minutes to an hour before going to bed. Especially since I have good control of myself, I won’t read more than 3 chapters per day, even when I get obsessed with a novel. So for a 300-page Chinese novel, it could still take me about 2 to 3 weeks to finish. The pandemic finally forced me to seriously read an English novel. And guess how long it took me to finish it? Nine months for a 400-page English novel! To compare the speed of reading, my Chinese reading speed is almost 15 times faster than that of English!
This very first English novel I finished, The Glass Bead Game by Hermann Hesse, was actually originally written in German (German book title: Das Glasperlenspiel). So if I ever learn German in the future, it will probably take me another two to three years to finish the original version of the book… But anyway, before sharing my thoughts on the book, I must say that reading an English novel (too bad the original language of this book is not English) is a completely different experience compared to reading a Chinese novel. On one hand, the grammar and the sentence structure build up an exotic atmosphere. On the other hand, the word choice (although I don’t know too many vocabularies so I have to look up many words during the reading) adds another layer of richness and texture. Let me make an analogy: translating an English novel into Chinese is like compiling a piano sonata into a violin version. So, of course, the sonata can be played beautifully even under the disguise of a violin, but undoubtedly there are some subtle ideas and feelings from the composer that can only be expressed on a piano.
Prologue - On the enlightenment of scientific research and some recent thoughts and reflections
After reading The Glass Bead Game, I had some brand-new reflections on scientific research. What is scientific research? Everyone probably has a very different answer to this question. Moreover, people’s comprehension might also change throughout their lifetime. To avoid misunderstanding others’ interpretation of scientific research, let me try not to give a straightforward answer to this question but instead talk about my own understanding at the different stages of my life!
My enlightening moment of science happened much later compared to most people here at Harvard. When I was a kid, my parents tried very hard to provide me with a less competitive environment and allowed me to explore different possibilities. And my hyperactive personality also naturally brought me to spend most of my time on sports and exercise. At that time, learning was simply a “citizen’s duty” to me and research was nothing more than a star in the sky that I knew existed but never really thought about it. The only impression was probably about some classmates who worked really hard on high school scientific fairs in order to get into top universities.
In the first three years of my undergraduate study, I started to get exposed to some interesting knowledge, including the beauty of mathematics, the complexity of history, the profundity of sociology, and the abundance of philosophy. The way knowledge was taught and formed completely opened up my passion and curiosity for learning. This made me really want to stay in such an environment so that I can keep consuming these mental nutrients. But how can I stay in such an environment forever? After consulting with many people, I realized I have to “do research” to exchange for the ticket of staying in academia. However, what is doing research? To the young and naive me at that time (and probably also for most people), the pictures in my mind were of great scientists like Einstein sticking out his tongue while writing alien equations on a blackboard or hustling among indescribable machines.
Nevertheless, as a computer science major, the so-called “research” seems to be quite different from the normal picture. Some classmates work hard all day trying to make a robot play soccer, while others bury themselves in gigantic programming development projects, and still others are always waiting for the training of their machine learning models. To me, as a person who loves abstract thinking, none of these seem to be the knowledge that I am interested in. Probably the only time I found excitement was in a software engineering project where the professor recommended that I learn Design Pattern to apply in a big program. I was so obsessed with the elegant object-oriented concepts in Design Pattern; however, these beautiful abstract concepts are never the leading character of a research project.
Unexpectedly, in the last year of my undergraduate study, I settled myself in doing theoretical computer science research after a huge detour. There were not so many people in Taiwan studying theoretical computer science, so there was no concrete research problem to work on, and not too many people to discuss with. Nonetheless, on the bright side, such an environment provided me the freedom to swim in the ocean of knowledge. I read as many papers and books as I wanted and wrote a bunch of high-quality notes. Looking back, it was really a happy and spiritually fulfilling period of time.
Later on, I started my Ph.D. journey at Harvard and ambitiously wanted to keep learning as much as possible like a sponge. Meanwhile, I also expected myself to make new contributions in the field through my research. Year after year, I gradually realized the pure beauty of knowledge and learning that had attracted me in the very beginning is not completely the primary aim of frontier scientific research. Some people might even look down on those who spend too much time on learning rather than producing as many research papers as possible. I began to comprehend the criticism of Thomas Kuhn on the so-called Normal Science that I learned a long time ago in a class about the philosophy of science. The recent reading of The Glass Bead Game was the last straw that struck me on my head. All of these led me back to the very fundamental and basic question: what is scientific research? What is it for?
The Glass Bead Game
After reading The Glass Bead Game, the philosophical and spiritual revelation was definitely no less than the first time I learned modern mathematics back in college. After ideating for a few weeks, I still could not find a satisfying way to start the article. So, I decided not to directly talk about my thoughts and feelings; instead, I’ll quote some of the paragraphs in the book (without spoiling the contents) and write some thoughts related to those paragraphs. The sentences and the page numbers come from the English translation by Richard Winston in 1969. In the Chinese version of this blog post, I also tried to further translate these paragraphs into Chinese. So, if you can read Chinese, please take a look!
The pursuit of perfection and purity
There is truth, my boy. But the doctrine you desire, absolute, perfect, dogma that alone provides wisdom, does not exist. Nor should you long for perfect doctrine, my friend. Rather, you should long for the perfection of yourself. The deity is within you, not in ideas and books. Truth is lived, not taught. Be prepared for conflicts, Joseph Knecht, I can see they have already begun.
Page 83.
As an extremely fortunate person, except for some financial pressures from my family, my parents have given me great freedom to choose my life path according to my instincts and passions. As a result, my life has been filled with idealistic colors, and I care very little about practical affairs. After being exposed to knowledge from all those nicely packaged disciplines, the pursuit of perfection and purity has become even more deeply ingrained in my mind. It was around the third year of my Ph.D. when I started to explore cross-disciplinary research and became aware of the huge gap between theory and reality. Especially after delving into the questions in biology, I began to doubt the belief in the existence of a theory of everything. My philosophy was seriously challenged. It felt like learning that Santa Claus is not real and realizing that the world is not as simple and beautiful as I imagined.
Believing in the existence of a perfect and pure doctrine is a romantic choice. Or, it is a relatively simple choice. As Nietzsche said, “God is dead,” doubting one’s own religion or even abandoning it will lead to a road that is filled with fights, conflicts, and confusion. But perhaps, this is the only road that leads to the real world?
The value of knowledge, life, and existence
At that time I was ambitious to work out a history of the sonata from a new point of view; but then for a while I stopped making any progress at all. I began more and more to doubt whether all these musical and historical researches had any value whatsoever, whether they were really any more aesthetic substitute for living a real life. In short, I had to pass through one of those crises in which all studies, all intellectual efforts, everything that we mean by the life of the mind, appear dubious and devalued and in which we tend to envy every peasant at the plow and every pair of lovers at evening, or every bird singing in a tree and every cicada chirping in the summer grass, because they seem to us to be living such natural, fulfilled, and happy lives. We know nothing of their troubles of course, of the elements of harshness, danger, and suffering in their lot. In brief, I had pretty well lost my equilibrium. It was far from a pleasant state; in fact it was very hard to bear.
Page 101.
This paragraph truthfully describes my life in the past year. The longer I stay in academia, the more research experience and maturity I have gained. However, it is the deeper understanding of the field that has given birth to doubts about the meaning of research. Outside the experts in the field, what is the value of obtaining a few more “research results”? When I try to answer this question honestly, I realize that the main value seems to be my own happiness. This happiness includes the satisfaction of curiosity, the sense of achievement in solving a problem, the vanity of being recognized by others, and the usefulness of producing something.
Reflecting on these questions about value is not a challenge to the real value of research but rather a self-reflection on what I really want. If I were to sacrifice my life, family, and health to make a significant contribution to science, is this really what I want? If so, why is there sometimes so much struggle deep in my heart? Or maybe the joy from research is no longer as strong as it was in the past? Value is not an absolute measure; it adapts and changes with time and space. How can I know if my own values are gradually changing and how can I face them?
Doubting the meaning of learned
What was important to him were his studies, all of which now centered around the Game. Another preoccupation was, perhaps, that one question of whether the Game really was the supreme achievement of Castalia and worth devoting one's life to. For even as he was familiarizing himself with the ever more recondite mysteries of the Game's laws and potentialities, even as he became more and more at home in the labyrinths of the Archives and complex inner world of the Games' symbolism, his doubts had by no means been silenced. He had already learned by experience that faith and doubt belong together, that they govern each other like inhaling and exhaling, and that his very advances in all aspects of the Game's mirocosm naturally sharpened his eyes to all the dubiousness of the Game.
Page 134.
We talked about the “value” of knowledge in the previous paragraph, and in this one, the main character starts to think about the “meaning” of what is learned. Value and meaning may sound very similar, but if you think carefully, the former is more about the feeling of objective materials and sensation, while the latter contains subjective spiritual and emotional attachment. For example, when you criticize the research of a scientist or the work of an artist for having no value, it might deny the objective and practical value, but their research and work definitely have a special meaning to them.
A thing could be very valuable but meaningless. Take an extreme (fake) example: if a great baseball player had set up many records during his professional career and left beautiful memories within his fans. However, suppose he actually hates baseball due to bad memories from his childhood hash training, and he just played baseball for the money. Even though what he has been doing is quite valuable to his fans and society, it is meaningless to him. Perhaps if he had other skills, he would have been much happier being a chef rather than a baseball player!
Meaning is a much vaguer concept compared to value. Meanwhile, people often pursue meaning once they have achieved a certain level of value in their life. That is to say, asking someone to do something that is valuable but meaningless to him/her could be very painful. On the other hand, if the thing is meaningful to him/her, then one would often enjoy the process a lot even without practical values. In such a case, meaning has great personal value. And from many examples of artists and even scientists, we can see that time might also change how society values something.
But not only value, meaning can also change. In this paragraph, the main character deeply doubts in his heart what he had been studying. I found this paragraph brilliantly depicts the main character having even more doubts after having a deeper and better understanding of the field. This is such an ultimate demonstration of intellectual honesty that woke up the anxiety in my mind. For my own field, I have enjoyed both the learning and research process very much and still do so nowadays. However, after getting more and more exposure to other fields in the past two years, there’s an indescribable concern arising inside me (perhaps this had been ideated since this blog post). Of course, there haven’t been many changes in my field, and its meaning to other people should not differ too much. But because of my own exploration and growth, I have to start rethinking about what the meaning of the thing I’m working on is.
The Utopian of purity and abstraction
And we go even further into the realms of pure mind, or if you prefer, pure abstraction: in our Glass Bead Game we analyze those products of the sages and artists into their components, we derive rules of style and patterns of form from them, and we operate with these abstractions as though they were building blocks. Of course all this is very fine; no one will contend otherwise. But not everyone can spend his entire life breathing, eating, and drinking nothing but abstractions. History has one great strength over the things a Waldzell tutor feels to be worthy of his interest: it deals with reality. Abstractions are fine, but I think people also have to breathe air and eat bread.
Page 279.
Recently, I watched the TV series “Upload” with my roommates. It is a story about people who can upload their souls to a cloud server and live there after their death. Just from this one-line description of the setup, one can already imagine lots of interesting stories and questions that can be developed, and the screenwriter, as well as the director, indeed did a very good job making the whole TV series fascinating. Suppose such technology comes up in the future, would you like to “upload” yourself and live a life without physical and physiological constraints and do whatever you like to do?
In some senses, Castalia (a place in the book where all the game masters gather and live) in The Glass Bead Game is like a cloud server. Everyone in Castalia only needs to focus on the game and try to be better and stronger. They don’t need to worry about other mundane and practical burdens as well as problems from the past. Similarly, some fields in our own world also more or less evolve into such a state, immersed themselves in the beauty of purity and abstraction like the “Qintan” in the Wei-Jin period of Chinese history.
One thing I found interesting and puzzling about this paragraph is: why does the author compare the Glass Bead Game with history? In particular, what does “it deals with reality” want to express? Compared to now and the future, history lives in the past and hence like the abstract world, which is also not really existing at the moment. History studies the people and events from the past, and probably the only practical value is “knowing the present from learning the past.” From this aspect, History indeed bears a lot of similarity with a pure and abstract discipline. However, the major difference between the two is that at least history did happen in reality. While abstract disciplines like math and philosophy sometimes have very practical applications, intrinsically, they exist in the Utopia of purity and abstraction.
In fact, the author didn’t explicitly mention “Utopia” in the book. But I purposely call a pure and abstract world (like the Glass Bead Game in the book or math and philosophy) as a Utopia. In such an abstract world, we basically only think about the perfect side of ideas, and hence in other words, it is really like an escape from facing reality. We should not forget that we ultimately live in this very real world. But it’s likely to say that within ten or more years, the technology can realize the setting in the TV series “Upload.” Perhaps the abstraction will become the new reality?
The role in the society
These fine teachers out there are, strictly speaking, the only ones among us who are really carrying out the purpose of Castalia. Through their work alone we are repaying the nation for the many benefits we receive from it. Granted that every one of us brothers of the Order knows that our supreme and most sacred task consists in preserving the intellectual foundation of our country and our world. That foundation has proved to be a moral element of the highest efficacy, for it is nothing less than the sense of truth - on which justice is based, as well as so much else. But if we examine our real feelings, most of us would have to admit that we don't regard the welfare of the outside as well as inside our tidy Province, as the chief thing. In fact, it is not at all important to us. We are only too glad to leave it to those brave teachers out there to pay our debt to the world by their self-sacrificing work, and so more or less justify the privileges we enjoy, we Glass Bead Game players, astronomers, musicians, and mathematicians. It is part of the above-mentioned arrogance and caste spirit that we do not much care whether we earn our privileges by accomplishments. Even though our abstemious way of life is prescribed by the Order, a good many of us plume ourselves on it, as if it were a virtue we were practicing purely for its own sake instead of its being the least that we owe to the country that makes our Castalian existence possible.
Page 350.
There’s a friend who once shared on Facebook, after receiving an award for distinguished teaching, that an old professor in his department told him on his first day of being a professor: “Teaching is the core of being a professor, while research is something auxiliary and additional.” I always find this saying quite intriguing. So, for a professor or a researcher in an academic institute, what is their duty to society? Producing top research and advising younger generations - which one is more central?
Normally, people might treat this as a binary question. Some people are good at research while some are good at teaching. Maybe a minority of them are good at both, but most of the time, people seem to fail on both. But if you think carefully, the core of doing research is also a process of passing on knowledge. Every (scientific) research is built on communication: at the beginning being recognized by the experts in the field, then maybe starting to have some follow-up works, some even starting to influence other fields and some even being written into a textbook. In the end, it slowly turns back to the society and flows into the river of history.
So to me, research is another form of teaching. Its foundation is still about passing on knowledge. As a member of academia, our duty to society revolves around learning, discovery, and passing on knowledge. In this paragraph, the author sharply criticizes the “Glass Bead Game players” who only focus on learning and discovery. This really resembles and satirizes the current situation in academia. But anyway, as a Ph.D. student, I probably don’t have the position to say too much. And this, in the end, is a personal choice in this world of survival of the fittest. Too much criticism might only lead to antipathy, so I just expect myself to remember these fundamental values and meanings deeply in my heart.
Awakening and reality
I never thought of those awakenings as manifestations of a god or daimon or of some absolute truth. What gives these experiences their weight and persuasiveness is not their truth, their sublime origin, their divinity, or anything of the sort, but their reality. They are tremendously real, somewhat the way a violent physical pain or a surprising natural event, a storm or earthquake, seem to us charged with an entirely different sort of reality, presence, inexorability, from ordinary times and conditions. The gust of wind that precedes a thunderstorm, sending us into the house and almost wrenching the front door away from our hand - or a bad toothache which seems to concentrate all the tensions, sufferings, and conflicts of the world in our jaw - these are such realities. Later on we may start to question them or examine their significance, if that is our bent; but at the moment they happen they admit no doubts and are brimful of reality. My 'awakening' has a similar kind of intensified reality for me. That is why I have given it this name; at such times I really feel as if I had lain asleep or half asleep for a long time, but am now awake and clearheaded and receptive in a way I never am ordinarily.
Page 395.
I always feel that life is a journey of continuous awakening and recognizing the truth and reality. Think about the first time you had delicious sashimi, the first time you listened to beautiful music, the first time you were touched by a mathematical proof, or the first time you looked over the whole city from the top of a mountain. After experiencing something, the way we see the world is no longer the same. As our vision and knowledge expand, it is hard to turn back to the original simple mindset. Our appetite becomes more and more difficult to satisfy; we start to hear the delicate ideas in a piece of music, pursue the extremes of abstract thinking, and yearn to travel to every corner of the world. Awakening can be either large or small, but usually, people are not aware of it at that moment. After accumulating enough levels of awakening, we suddenly realize that we are no longer the same person.
Some awakenings can totally change one’s value system. For example, during the age of enlightenment, people walked away from religion and emotion towards science and rational thinking. In this confession, the main character from the book uses vivid analogies and examples to stress the violent shock he received from the sense of reality from the awakening. After reading The Glass Bead Game, I experienced a similar awakening. Now, when I think about my research or things in life, I consider some aspects that I never thought about before. In particular, the meaning and value towards a thing begin to change. When I look back at myself a few years ago, a foreign feeling shocks me, and I’m very surprised by why I cared so much about certain things and why I sacrificed so much for the important ones.
Awake or sleep
Everlasting night, the wind gently touches
Dazzling day, the living vigorously bustles
Oh the ferryman
Where's the next harbor'?
Epilogue
What impressed me the most about The Glass Bead Game is that the author never delivers dogmatic preaching on what he really wants to say. Through the growth and life path of the main character, these ideas naturally emerge from the reader’s heart, and one feels that “Ah ha, he wrote out my own fuzzy feelings and thoughts!” Even in the end of the story, there’s a feeling about how the story is going to end when I was still a few pages away. The author finally uses beautiful and fluent words to conclude the story in a supposedly surprising but not-so-surprising way, like an everlasting hymn.
Returning to the question in the very beginning about the meaning of scientific research to me, I think instead of using another thousand words to elaborate, why not simply use the above six paragraphs that deeply resonate with my feelings? Let the reader guess, think, and feel about my awakening moment!
My Third Ph.D. Year
17 Aug 2020(中文版原文連結)
One week after Liqiu, the heat in New England was finally relieved, if only temporarily. Perhaps this year is truly hotter than previous years, or perhaps the never-ending quarantine has made time feel particularly slow. The sudden pandemic has changed our daily lives as well as our perception of time. Now that autumn is approaching, it suggests the end of another school year.
Compared to the bewildering exploration in the first two years of my Ph.D., I feel more confused in the third year, despite having settled on some research directions and achieved some results. But what I mean by “confusion” here may not be as negative as it sounds. After all, if you stopped a graduate student on the Harvard campus, I believe the majority of them would also say they are confused about what they are doing. So perhaps the more important thing is to know what you are confused about. In my case, I mainly doubted my own ability in the first two years of my Ph.D. Now that I’ve crossed the midpoint of my Ph.D., it is “what research direction (or even life direction) I want to pursue” that has been constantly on my mind.
But anyway, before any serious discussion, let’s review what happened this year!
What I’ve done in the past year?
At around this time last year, I decided to invest more time studying and exploring theoretical neuroscience. By some funny coincidence, I started to collaborate with my best friend, Brabeeba, a Ph.D. student at MIT. After countless discussions (and debates) in MIT’s student cafeteria, Harvard’s dorm, and even the Boston Symphony Orchestra, we successfully solved the research problem we were looking at: giving the first convergence rate analysis for a biologically plausible learning rule. The techniques we developed from that work also led us to a cute follow-up work.
This close collaboration experience with Brabeeba not only brought me more confidence in doing independent research (because this work was completely done by ourselves without any guidance from professors), but also taught me a lot about how to work with other people. Brabeeba and I have very different research styles to the extent that we are almost completely complementary to each other. On the bright side, such complementation can push research progress swiftly. Whenever I got stuck, Brabeeba could always come up with some new ideas to circumvent, and whenever he felt that the problem came to a dead end, it was me who found a way out. However, the difference between us could also bring up undesirable conflicts, especially when it comes to dividing opinions on research direction or the presentation of writing; we debate all the time. To be honest, sometimes debate is a frustrating process, especially when the other person is your friend and/or your collaborator. But if you change your perspective, as long as the debate is healthy (meaning that no negative words are used), it can be very fortunate to have good and straightforward communication with someone. This helps to spot mistakes and ignorance and also provides diversity in the discussion. In the case of working with Brabeeba, we can usually turn disagreements into positive forces in the research. Additionally, it is very enjoyable to have a collaborator who is also one of your best friends!
As for my main research focus in complexity theory, frustratingly and unexpectedly, there is still no progress in most of the directions I’m interested in, but luckily one line of work finally has some non-trivial progress. The starting point is a simple question: how well can you approximate the maximum directed cut of a directed graph (Max-DICUT) with only logarithmic space (when the edges are given in a 1-pass stream)?
The trivial random sampling algorithm gives a (1/4)-approximation, while a previous work finds a (2/5)-approximation using a more clever idea. On the hardness side, the best-known previous impossibility result only ruled out a (1/2)-approximation. Namely, there is a gap between 2/5 and 1/2 in our understanding. In collaboration with Santhoshini and Sasha, we found that, surprisingly, neither 2/5 nor 1/2 is the true answer: the optimal approximation ratio for Max-DICUT is 4/9. Through related technologies, we thoroughly analyzed the best approximation factor of boolean 2CSP under the streaming model. After Madhu joined us at the beginning of the summer, we have made significant progress in this direction.
Finally, in collaboration with Boaz and Xun, we tried to challenge Google’s quantum supremacy experiment. At first, Boaz and I had a simple classical algorithm, but the analysis was not very satisfying. Xun, a postdoc in the theoretical physics department at Harvard, heard that we were working on this problem and introduced the tensor network technique (which is a very common tool in theoretical physics) to us. It turns out that tensor networks can directly give a rigorous analysis of the algorithm.
In the ongoing follow-up project, we use theory and numerics to demonstrate the performance of our algorithm, due to some fundamental obstacles in the theoretical analysis. This kind of research methodology is very rare in theoretical computer science but is typical in theoretical physics. In the past, I always felt that if the result could not be rigorously demonstrated in mathematics from the beginning to the end, then it does not count as a “theoretical” research. However, after intensively working with Xun this time, I gradually started to appreciate this kind of physics-style research methodology. Sometimes, a theoretical research with a bunch of assumptions might not provide more insights than a research with part of rigorous mathematics and part of experiments/simulations. But of course, this depends on the research problem. If it is a fundamental theoretical and mathematical problem, the requirement for mathematical rigor must be 100%. However, for more practical or interdisciplinary problems, finding a beautiful balance between theory and experiment may provide better insights.
New confusion?
This year, I have conducted research in three very different directions and fortunately have achieved some partial results. These experiences have built up confidence in myself, but what immediately followed was thinking about my future direction. First, how to allocate my time and how to prioritize these different directions. Second, what kind of research do I appreciate and want to pursue? Although the problems in complexity theory are indeed attractive to me, they sometimes also give me a sense of emptiness like playing intellectual games. This may be an unavoidable contradiction/paradox of pure theoretical research. On one hand, if you only look at the big problem without taking small steps, you may be stepping around at the same place forever. On the other hand, if you spend all your time on small incremental things, you might never touch the real fundamental problem. However, worrying and being stuck in this paradox is not going to help. I guess what I can do is reflect on this issue regularly. What is complexity theory for me? Is it an arena to prove my intellectual power? Or does it carry a sense of mission to solve fundamental problems?
Therefore, at the beginning of the year, I started to have the idea of pursuing another Ph.D. (in Algebraic Geometry or related fields) in pure mathematics, mainly because after learning more mathematics, I deeply felt that I’m just touching the surface of real mathematics. Furthermore, much of the deep mathematics has not been (seriously) considered and applied to complexity theory. Also, learning these mathematics requires the right “language”. If I stayed on the current path, I would not have the opportunity to learn these languages well. It’s like it is (almost) impossible to learn English well if you are always in a non-English native environment. But having said that, pursuing a Ph.D. in mathematics is just one of the possible ways to achieve the goal; maybe there is another better way? Anyway, it’s too early to decide. I can wait until this time next year to worry about it…
Facing the future
People are always changing. This is probably my biggest awakening in the past few years. The changes can be in the ability, vision, or even personality and values. This tells us that what we think we want in the future at this moment may not necessarily be what we really want in the future. In my case, it’s quite funny in retrospect that the reason why I went to academia was not that I like doing research (after all, compared with most people, I started to do research relatively late), but because I love learning new things. At first glance, the academic road seems to provide a lifestyle of life-long learning that can make me happy. Fortunately, after many years, I also found myself enjoying the feeling of exploring the unknown in research. In particular, the final results of several projects were very different from what I expected at the beginning, which made me deeply attracted to the mysterious nature of doing research. This is even more true in the research direction. A year ago, I couldn’t expect that I would be working on the research problems that I mentioned above. Similarly, I believe it is impossible to predict what I will be doing a year later.
A few weeks ago, during a walking meeting with Boaz, I told him that I had recently encountered a career crisis: I don’t know which direction to go, and I don’t know where I will be going in the next five or ten years. Boaz’s advice was simple, but it was an enlightening moment for me. He told me to just think about what I’m going to do in the next year! Maybe it’s because there are too many people’s examples to look at before the Ph.D., so I can always plan my future plans in advance. However, when it comes to the stage of independent research, everyone must create their path. Maybe some people can see the development in the next few years, but in most cases, the future steps highly depend on the immediate next step. In the end, everyone is changing, and the world is also changing (e.g., the sudden pandemic), so in addition to being bothered by the plan for long-term future, a very important ability is to find a good direction in each moment and work as hard as possible. This is probably also true for other life topics other than doing research.
My friends always told me not to overthink. Indeed, thinking less may make myself less annoyed and have a happier life. But for me at least, thinking more and deeper often makes me more aware of what I really want. While we all want to live happily, what makes oneself happy is sometimes not that obvious. Maybe the answer (if there’s any) is hidden in the confusion by wild thoughts!?
My Second Ph.D. Year
21 Jul 2019(中文版原文連結)
In the blink of an eye, my second year at Harvard had come to an end. Now, the summer is halfway through, and soon, I’m going to cross the middle line of my Ph.D. life. Compared to two years ago, I have perhaps made some progress and improvement, yet I still fall short of what I had expected of myself. During the CCC (Computational Complexity Conference) this summer, my friend Lijie gave me lots of his thoughts and advice. Although those might not be completely applicable to me, they indeed remind me to rethink my future plan and direction for the rest of the time.
What have I done in the past year?
In retrospect, this was a really frustrating year. The drama in life influenced my focus and time spent on research. Meanwhile, the choice in research direction was also not very ideal. The results in both research and learning seem to be below the bar.
This year, I have mainly been focusing on algebraic complexity, in particular, matrix rigidity and border Waring rank. The former is a research program that studies a combinatorial problem (i.e., circuit lower bound) in an algebraic setting. The ultimate goal is to (explicitly) construct a matrix that is far away from low-rank matrices into $\ell_0$ norm. This will imply super-linear lower bounds for logarithmic depth circuits, which will be a breakthrough in our field. I really like the idea of matrix rigidity because it turns a seemingly complicated and arbitrary structure (i.e., circuits) into an algebraic problem that is much more convenient to think about. Nevertheless, after almost 50 years since its conceptualization, there has been very limited progress in matrix rigidity. In the past year, my collaborator Sasha and I have tried multiple old and new approaches to attack the problem and even lowered the goal. However, it always feels like we are just paddling on the surface of a bottomless ocean. As for the other line of research about border Waring rank, initially, I just found the math to be interesting and then spent a semester learning representation theory to understand the paper. But once I finally understood what’s going on in the paper, I further realized that more math (e.g., Lie algebra, algebraic geometry, etc.) is needed for me to make some real contributions to the problem.
Looking back, I seemed to pick and dig into a research problem simply depending on my interest and neglect whether me or the people around me have the ability to tackle the problem. I know we were always told to try our best and not underestimate ourselves. But in terms of pursuing frontier research, now I believe it is very important (and sometimes necessary) to arm yourself with enough gears and surround yourself with the right resources and experts. Like what Lijie asked me: “Why should this problem be solved by you?”. Other than having more time to think about the problem, what’s the strength I have over those experts in the field?
Positioning myself
Perhaps this goes back to a basic but important question: what is my position in the field (or even the world)? Every researcher has their own strengths and weaknesses. Some excel in high-level intuition, while some are skillful in complicated calculations. Some know various math tools, while some are aware of the methodologies in different fields. And of course, some people, like me, may not be good at any specific thing… But anyway, I guess it is very normal for a Ph.D. student to feel that they are not good at anything. However, this should not be the case after graduation. One has to be the top person in the world in at least one skill to survive in academia. So then this boils down to the next important question: what skill do I want to cultivate for the rest of my Ph.D. and how?
In my case, I have always expected myself to be a broad-minded person (in TCS, math, or even in whole academic fields) and, at the same time, specialize in a few small directions. So far, it seems that I am not doing a very good job along either axis. On the broad side, I might get exposed to a wide variety of subjects without significant internalization. For many things, I am still at the level of “having heard the jargon/terminology before but not yet having the ability to have a meaningful conversation on them.” On the deep side, I really want to specialize in arithmetic circuits and boolean circuits. But I am currently still in the situation in which “I know many important results and key intuitions, but I am not yet able to fluently jump between different concepts and, let alone, ask interesting new questions.”
So, in the end, I have always vaguely positioned myself in certain directions. The problem is that I have not pushed hard on myself towards these directions. I am sometimes too lazy and easily get distracted by other stuff, hence deviating from the main line. As there is not much time left, I should carefully think about how to push myself back to the road I want.
Next step
Balancing time for self-development and a specific research problem is crucial. One must carefully consider before investing a significant amount of time. Do you truly enjoy this research problem? What is the meaning of this research to you? Are you ready to tackle it now? The two directions that I’ve been working on in the past year seem too specific, and I’ve lost sight of the big picture. Additionally, I’m not entirely prepared from a technical standpoint.
As someone who wants to specialize in arithmetic circuits and boolean circuits, the key problems like lower bounds and derandomization exist, and there are a few different circuit models with their own frontiers and barriers. Currently, I only have a vague understanding of the state-of-the-art results in most settings and lack a crystal-clear understanding of what the bottleneck is and what the potential breakout point could be. Therefore, the next step is quite apparent: read more, think more, internalize the knowledge, and build my library. I really hope to regain my good old habit of keeping notes rather than having blurry concepts in my mind.
In addition, mental stability is crucial, particularly in TCS, where smart people abound, and the field moves rapidly. One must find a way to be less influenced and keep moving forward, and most importantly, positioning oneself and not isolating from others. Sometimes, I feel that choosing this path is self-torture. Nevertheless, the sense of fulfillment and satisfaction it brings is extraordinary. We only get one shot in life, so let’s not leave any backdoor for ourselves and keep striving!